计及电量电价弹性的主动配电网多时间尺度优化调度

梁 宁, 邓长虹, 谭 津, 陈亚红, 夏 沛, 梁效文

(武汉大学电气工程学院, 湖北省武汉市 430072)

0 引言

随着环境的恶化和电池等技术的不断发展,电动汽车和可再生能源越来越受到各国的重视和发展[1-3]。但大量电动汽车、可再生能源接入配电网,将对现有配电网造成广泛的影响,如降低配电网的经济性,增大负荷峰谷差、节点电压偏移和网损[4-5],进而影响配电网的供电可靠性等。因此,兼容电动汽车、可再生能源发电的主动配电网技术应运而生[6-7]。而如何对主动配电网内大量电动汽车、储能、柔性负荷和可再生能源进行有效的调度,以平滑负荷曲线、减小配电网运行成本,并有效参与到当前电力市场中,成为亟待解决的问题。

在含可再生能源、储能和电动汽车的配电网优化调度方面,国内外专家学者开展了大量的研究工作。文献[8]提出了一种主动管理电动汽车充电的调度方法,从而达到减少配电网损耗、节点电压偏移和负荷峰谷差的目的。文献[9]提出了一种含电动汽车不同节点随机充电的配电网调度方法。该方法在兼顾配电网安全性、经济性的同时,最大限度地满足电动汽车的电量需求,并减少电池的退化成本。文献[10-11]针对可再生能源出力随机性和波动性的问题,基于模型预测技术,提出了一种含可再生能源的主动配电网多时间尺度优化调度策略。文献[12]针对风电、光伏、储能和柔性负荷的接入,对主动配电网带来的问题,提出了一种多源协调调度的总体框架。随着电力市场化改革加快进行,电价在主动配电网中的调节作用越来越明显[13]。文献[14]在电力市场环境下,建立了一种负荷和峰谷电价协调的数学模型。文献[15]在基于分时电价模型和电量电价弹性矩阵的基础上,研究了电价引导用户柔性负荷功率的模型,从而改善了主动配电网的供电可靠性。

此外,部分学者还提出了含可再生能源的微电网多时间尺度优化调度方法。文献[16]在日前和实时调度阶段分别结合光伏和负荷的短期和超短期预测数据,提出了一种含储能和可再生能源的微电网多时间尺度优化调度方法。

上述文献对本领域研究奠定了坚实的基础。然而还存在以下不足:①在电力市场环境下,对配电网中电动汽车充电负荷的引导不足;②在优化模型方面,现有研究对配电网中可调度资源挖掘不够充分,导致策略制定者和执行者之间存在一定偏差;③基于现有手段,可再生能源预测存在一定偏差,在配电网层面,现有方法在多个时间尺度上,协调电动汽车、储能和可再生能源的研究不足。

针对上述问题,在深入分析电量电价对弹性负荷引导的基础上,制定了电价引导电动汽车充电的模型,并进一步提出了一种主动配电网多时间尺度优化调度方法。该方法基于可再生能源短期和超短期预测数据,综合考虑电动汽车、储能和柔性负荷在多个时间尺度上的调用。最后采用改进粒子群算法对所建立模型进行求解,验证所提方法和模型的有效性。

1 主动配电网架构和调度方法

1.1 主动配电网架构

智能配电网是基于先进的信息网络架构,实现配电网的信息化、智能化[17]。而主动配电网是未来智能配电网发展的高级阶段,可以实现用户和电网之间的互动,满足未来各种关键技术的发展[18]。图1所示为一种未来主动配电网的典型架构,与传统配电网相比,有以下不同:①含电动汽车、可再生能源、储能、柔性负荷和刚性负荷等多种电源和负荷结构形式;②配电网中多种单元可主动参与系统的调度;③配电网中大规模电动汽车和可再生能源的接入,增大了系统功率的波动。

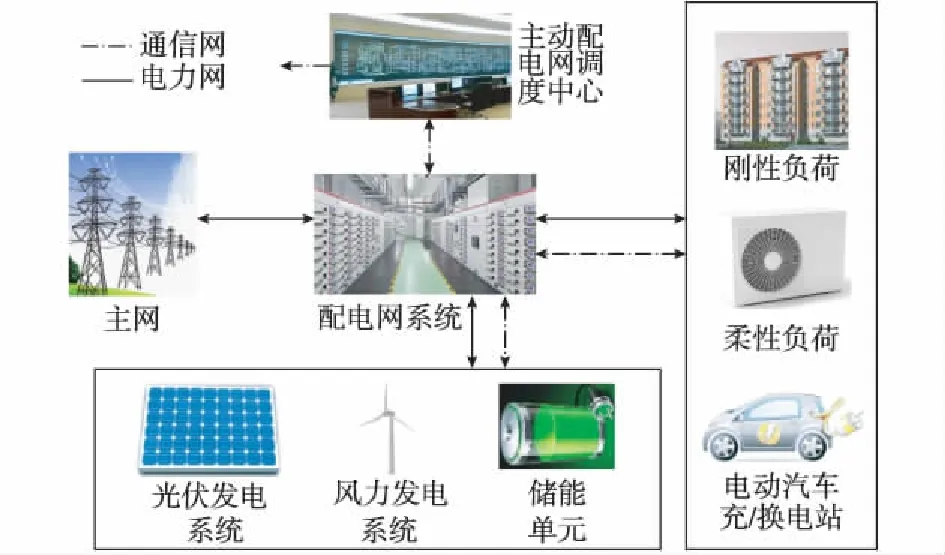
图1 典型主动配电网架构Fig.1 A typical architecture of active distribution network

1.2 调度方法

主动配电网的调度问题是一个高维度、非线性和多约束的优化问题,且调度计划需兼顾多方利益。调度的目的是在最大限度地吸纳可再生能源出力的前提下,以负荷和可再生能源预测数据为基础,充分考虑电动车主的利益,对配电网中电动汽车、储能和柔性负荷进行统筹协调,以降低可再生能源和电动汽车对配电网的影响,确保配电网运行成本最优,负荷特性得到优化。

本文制定的调度模型,在研究电量电价弹性模型和电动汽车充电负荷特性的基础上,制定了一种计及电量电价弹性的电动汽车充电模型。该模型充分考虑电动汽车负荷在电力市场电价机制下进行引导。然后,基于电力市场下的峰谷电价,通过日前和实时阶段的协调调度,有效发挥系统中电动汽车、储能和柔性负荷的作用。

2 多时间尺度调度模型

2.1 计及电量电价弹性的电动汽车日前充电模型

电量电价弹性是指电价的变动所引起用户用电量的变化[19]。由于确定该非线性函数非常困难,经济学上一般对其进行线性化处理,得到的各时段电量电价弹性系数如式(1)所示[20]。其中,当t=t′时,E(t=t′)为自弹系数,当t≠t′时,E(t=t′)为互弹系数。

(1)

式中:Ω0(t′)和Ω(t′)分别为t′时段的初始电价和当前电价;P0(t)和P(t)分别为t时段的初始功率和实际功率,由于本文日前阶段为24时段优化调度,各个时段用户的功率大小即为用电量大小。

由于电动汽车大部分时间处于停驶状态,只需在电动汽车离开充换电站时,其电池电量满足一定的水平即可。因此,在电力市场背景下,电动汽车充电负荷可受到当前和其他时段的电价水平综合影响,其充电负荷不仅可以在单个时段进行削减,而且可以在多个时段间进行转移,具有一定的自弹和互弹性。

对电动汽车充电负荷在单个时段和多个时段之间的削减和转移的量,运用电量电价弹性[21]进行推导计算(见附录A),可得各个时段的充电功率如式(2)所示。并将此充电模型引入主动配电网日前优化模型中的功率平衡等式约束。在多时间尺度模型中,不考虑对电网放电,电动汽车作为配电网优化调度中的一部分,对其充电负荷进行优化调度。

PEV(k,t)=

(2)

其中

(3)

(4)

式中:PEV(k,t)为k类型电动汽车的总充电功率;PEV,0(k,t)为电动汽车总初始充电功率;k(k)为充电安全系数;Ω0(t)和Ω(t)分别为初始和当前购电电价;T为一个日前调度周期的总时段数,值为24;C(k)为一个调度周期内电动汽车总电量需求;tEV(k)为一个调度周期内电动汽车在站的平均时段个数;nEV(k,t)为可调度电动汽车在站个数;NEV(k)为电动汽车可调度总个数;S(k,l)为第l个电动汽车在一个调度周期内的行驶里程;W100(k)为电动汽车百公里耗电量。

2.2 日前优化调度模型

日前阶段采用配电网成本最小的经济调度模型,目标函数如下所示:

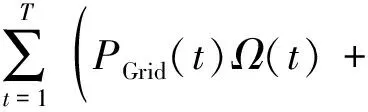
(5)

式中:PGrid(t)为从主网购电功率;δess为储能单元的调度成本系数;NL为配电网节点的总个数;PS(i,t)为第i个节点储能单元的充放电功率;CLoad(t)为柔性负荷的调度成本。

CLoad(t)如式(6)所示,包含可中断负荷的补偿成本函数fc(t)和激励负荷的激励成本函数fe(t)[22]。

CLoad(t)=fc(t)+fe(t)

(6)

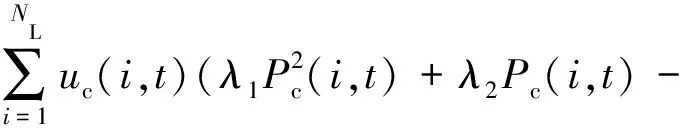
λ2Pc(i,t)kc(i))

(7)

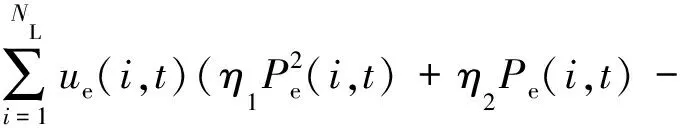
η2Pe(i,t)ke(i))

(8)

式中:uc(i,t)和ue(i,t)分别为第i个节点可中断负荷和激励负荷的状态变量,1表示被削减或激励,0表示未被削减和激励;Pc(i,t)和Pe(i,t)分别为削减和激励的值;λ1,λ2和η1,η2分别为可中断负荷的补偿系数和激励负荷的补偿系数;kc(i)和ke(i)分别为削减和激励负荷用户的意愿因子。

含电动汽车和分布式电源的主动配电网优化调度需满足以下约束条件。

1)功率平衡约束

(9)

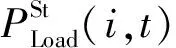
2)储能约束

(10)

E(t)=E(t-1)+Δtμc(t)PS(i,t)ηc+

(11)

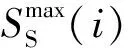
3)电动汽车约束

(12)

(13)

(14)

(15)

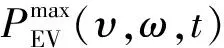
2.3 实时优化调度模型

由于光伏和风电的日前预测值存在较大偏差,而在超短期预测时,其预测偏差相对较小。所以在实时阶段,以风电、光伏、电动汽车和储能的总有功修正值最小为目标函数。优化目标函数如式(16)所示。

(16)

式中:T′为实时计划在24 h的总时段数,实时计划时间间隔为15 min,即每隔15 min滚动向前更新一次,一日共包含96个调度区间;ΔPWT(i,t)和ΔPPT(i,t)分别为第i个节点风电、光伏实时超短期预测相对于日前预测的误差;ΔPS(i,t)和ΔPEV(k,t)分别为储能单元和电动汽车实时计划相对日前计划的调整量。

实时优化调度同样需要满足功率平衡等式约束、储能和电动汽车相关约束,这些约束条件作为硬约束,在优化过程中必须严格满足。其中,由于频繁的充放电对储能单元寿命影响较为明显,所以实时计划中的储能充放电状态由日前计划给定,不做修改。

3 算例分析

3.1 系统描述和调度流程

本文采用改进IEEE 69节点配电网来验证所提模型的有效性,见附录B图B1。居民私家车具有代表性的是美国联邦公路管理局对居民电动汽车的调查报告[23],其中出行时刻和归来时刻服从正态分布,其概率密度函数分别为式(17)和式(18),日行驶里程服从对数正态分布,其概率密度函数见式(19)。

fs(x)=

(17)

fe(x)=

(18)

(19)

式中:μs=8.92;σs=3.24;μe=17.47;σe=3.41;μm=2.98;σm=1.14。

假设配电网中私家车接入数量为1 000辆,型号采用比亚迪E6型纯电动汽车[24],耗电量为0.196(kW·h)/km,行驶里程、出行和归来时刻采用式(17)至式(19)并运用蒙特卡洛抽样方法进行确定,由此可确定私家车一个调度周期内的初始电量总需求、充电开始时段和在站电动汽车个数;公务车参数采用宇通E7型纯电动汽车[25],能耗为0.35(kW·h)/km,本文假设接入量为50辆,日行驶里程为100 km/辆;公交车参数采用宇通电动公交天津示范工程数据,其日行驶里程为220 km/辆,能耗为0.96(kW·h)/km,假设接入量为50辆;假设出租车接入数量为50辆,采用换电和快速充电模式的出租车分别占50%,其中采用快速充电模式的出租车对充电的时效性要求较高,所以对其充电过程不进行优化。出租车换电时间为06:00—08:00和17:00—19:00的换班时间。各节点刚性负荷百分比见附录B表B1,储能单元参数见表B2,配电网向主网的购电电价,即一般工业分时电价见表B3,电量电价自弹和互弹系数见表B4,柔性负荷参数见表B5。可再生能源选取一年中预测误差较大的典型日预测数据,如图B2所示。并假设可再生能源全部消纳。

为验证所提模型的正确性和有效性,本文基于C++语言建立模型,运用改进粒子群算法[26]进行求解。调度流程如附录B图B3所示。

3.2 日前优化调度分析

在日前优化阶段,分别对3种工况下的优化结果进行对比。

工况1:电动汽车随机充电模式,即只要满足电动汽车充换电站的最大最小功率约束,就为新进入的电动汽车进行充电,对柔性负荷不做优化。

工况2:应用本文所提模型,进行优化求解。

工况3:储能和柔性负荷优化策略同工况2,以日前时段电动汽车和可再生能源波动平方差最小为目标[27],在满足多种约束的前提下,优化电动汽车功率。

3种工况下总负荷和初始负荷曲线如图2所示。和工况1相比,工况2和3下的负荷优化结果较为平缓,提高了配电网的供电可靠性,此外,工况3在时段1～6填谷效果较工况2略低。图3为工况1和2下储能、电动汽车和柔性负荷的优化结果,工况3下电动汽车优化结果见附录B图B4。可知本文模型能基于电力市场分时电价,有效优化电动汽车充电负荷、柔性负荷和储能单元。最后,通过潮流计算,得到配电网各节点的电压大小和网络损耗。以2种工况下配电网的负荷峰值时段为例,69节点电压大小如附录B图 B5所示,可知本文所提模型可有效提高配电网静态电压质量。表1所示为3种工况下配电网总的运行费用、网络损耗值对比、电动汽车充电费用和优化时间。可知在使用本文所提模型模式时,配电网的主网购电费用和网损均有所降低,且本文模型相对工况3效果更优,在降低计算时间方面效果明显。

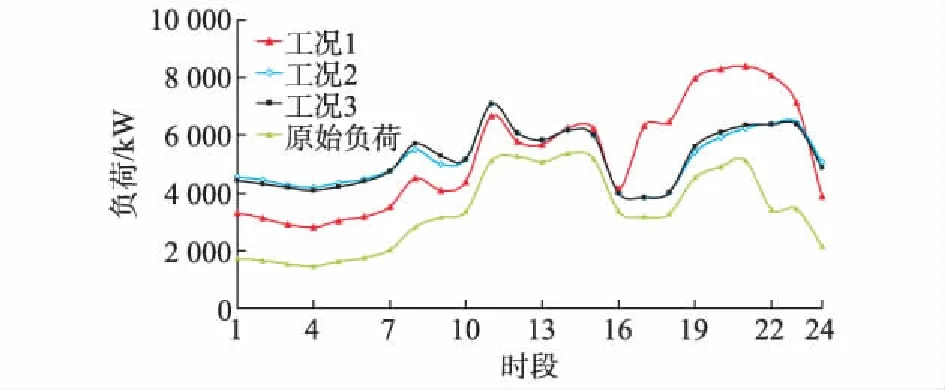
图2 日前调度负荷曲线Fig.2 Load curves of day-ahead scheduling

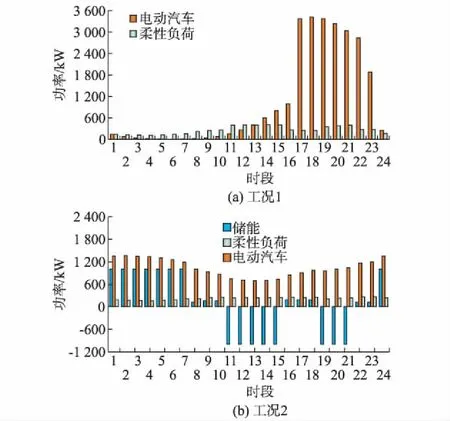
图3 储能、电动汽车和柔性负荷优化结果Fig.3 Optimization results of energy storage, electric vehicle and flexible load

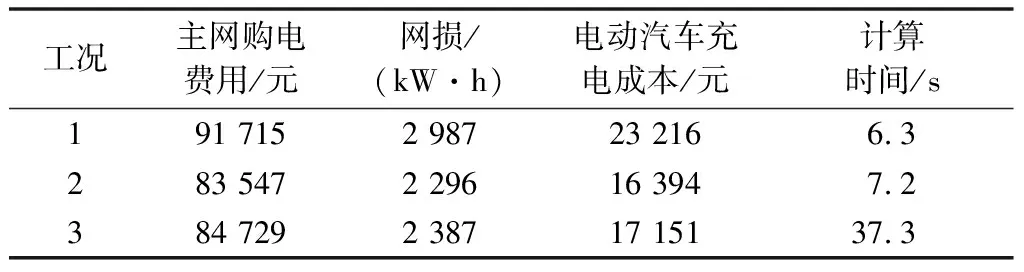
工况主网购电费用/元网损/(kW·h)电动汽车充电成本/元计算时间/s 191 7152 98723 2166.3 283 5472 29616 3947.2 384 7292 38717 15137.3

3.3 实时优化调度分析

以日前计划下的工况2优化结果为基础,并考虑风电和光伏短期预测偏差较大的场景。在实时计划中运用储能和电动汽车对预测偏差进行修正,并和修正前的优化结果进行对比。主网交换功率实时调度结果如附录B图B6所示。通过潮流计算,得到修正后实时阶段负荷峰值时段各节点电压如附录B图B7所示。图4所示为修正前后和主网联络线交换功率,图5所示为修正前后储能和电动汽车实时优化结果。

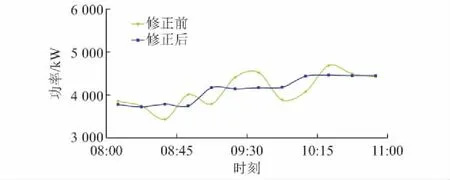
图4 修正前后和主网联络线交换功率Fig.4 Power exchange with main grid before and after correction

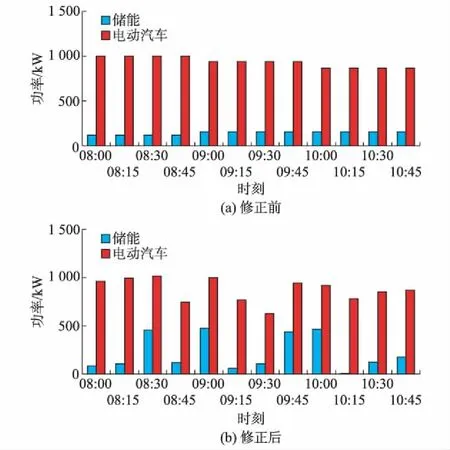
图5 储能和电动汽车实时优化结果Fig.5 Real-time optimization results of energy storage and electric vehicle

由图4和图5的仿真结果可以发现,本文模型可随风电光伏出力的快速波动,调节储能和电动汽车的实时计划,从而平滑风电光伏出力和主网购电功率波动,减小系统旋转备用容量,降低主网实时发电计划发布后自动发电控制(AGC)单元的调控压力。此外,实时计划流程耗时约1.6 s,日前和实时计划均满足在线调度需求。

4 结论

在电力市场背景下,本文针对电动汽车、储能、柔性负荷和可再生能源接入的主动配电网的技术特征,重点研究了主动配电网优化调度模型和方法。主要结论如下。

1)计及电量电价弹性的电动汽车充电模型,有效提升了电动汽车参与调度的积极性,同时降低了充电费用。“多级协调、逐步细化”的调度策略,通过协调优化调度电动汽车、储能和柔性负荷,实现了配电网对可再生能源的充分利用。

2)在日前阶段,以配电网经济性最优为目标,优化了电动汽车、储能和柔性负荷。此外,在优化配电网负荷曲线的同时,为提高主动配电网可靠性和经济性提供了有效的描述方法。

3)在实时阶段,利用储能和电动汽车最大限度地降低了可再生能源预测误差对系统的影响,从而提高了配电网供电可靠性,减小了系统备用,降低了主网AGC的调控压力。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参考文献

[1] ZHENG Y, DONG Z Y, XU Y, et al. Electric vehicle battery charging/swap stations in distribution systems: comparison study and optimal planning[J]. IEEE Transactions on Power Systems, 2014, 29(1): 221-229.

[2] HATTAM L, GREETHAM D V. Green neighbourhoods in low voltage networks: measuring impact of electric vehicles and photovoltaics on load profiles[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(1): 105-116.

[3] CHUAN H E, LIU T, LEI W U, et al. Robust coordination of interdependent electricity and natural gas systems in day-ahead scheduling for facilitating volatile renewable generations via power-to-gas technology[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(3): 375-388.

[4] ZAKARIAZADEH A, JADID S, SIANO P. Multi-objective scheduling of electric vehicles in smart distribution system[J]. Energy Conversion and Management, 2014, 79(3): 43-53.

[5] MEERWIJK A J H V, BENDERS R M J, DAVILA-MARTINEZ A, et al. Swiss pumped hydro storage potential for Germany’s electricity system under high penetration of intermittent renewable energy[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(4): 542-553.

[6] 陈星莺,陈楷,刘健,等.配电网智能调度模式及关键技术[J].电力系统自动化,2012,36(18):22-26.

CHEN Xingying, CHEN Kai, LIU Jian, et al. A distribution network intelligent dispatching mode and its key techniques[J]. Automation of Electric Power Systems, 2012, 36(18): 22-26.

[7] YANG Zhile, LI Kang, NIU Qun, et al. A self-learning TLBO based dynamic economic/environmental dispatch considering multiple plug-in electric vehicle loads[J]. Journal of Modern Power Systems and Clean Energy, 2014, 2(4): 298-307.

[8] CLEMENT-NYNS K, HAESEN E, DRIESEN J. The impact of charging plug-in hybrid electric vehicles on a residential distribution grid[J]. IEEE Transactions on Power Systems, 2010, 25(1): 371-380.

[9] KAVOUSI-FARD A, ABBASI A, ROSTAMI M A, et al. Optimal distribution feeder reconfiguration for increasing the penetration of plug-in electric vehicles and minimizing network costs[J]. Energy, 2015, 93: 1693-1703.

[10] 董雷,陈卉,蒲天骄,等.基于模型预测控制的主动配电网多时间尺度动态优化调度[J].中国电机工程学报,2016,36(17):4609-4616.

DONG Lei, CHEN Hui, PU Tianjiao, et al. Multi-time scale dynamic optimal dispatch in active distribution network based on model predictive control[J]. Proceedings of the CSEE, 2016, 36(17): 4609-4616.

[11] 肖浩,裴玮,孔力.基于模型预测控制的微电网多时间尺度协调优化调度[J].电力系统自动化,2016,40(18):7-14.DOI:10.7500/AEPS20151123008.

XIAO Hao, PEI Wei, KONG Li. Multi-time scale coordinated optimal dispatch of microgrid based on model predictive control[J]. Automation of Electric Power Systems, 2016, 40(18): 7-14. DOI: 10.7500/AEPS20151123008.

[12] 蒲天骄,陈乃仕,王晓辉,等.主动配电网多源协同优化调度架构分析及应用设计[J].电力系统自动化,2016,40(1):17-23.DOI:10.7500/AEPS20150520010.

PU Tianjiao, CHEN Naishi, WANG Xiaohui, et al. Application and architecture of multi-source coordinated optimal dispatch for active distribution network[J]. Automation of Electric Power Systems, 2016, 40(1): 17-23. DOI: 10.7500/AEPS20150520010.

[13] 周京阳,王斌,周劼英,等.市场机制下智能电网调度控制系统调度计划应用模型及分析[J].电力系统自动化,2015,39(1):124-130.DOI:10.7500/AEPS20141009020.

ZHOU Jingyang, WANG Bin, ZHOU Jieying, et al. Applied model and analysis of dispatching plan in smart grid dispatching and control systems under market mechanism[J]. Automation of Electric Power Systems, 2015, 39(1): 124-130. DOI: 10.7500/AEPS20141009020.

[14] AALAMI H A, MOGHADDAM M P, YOUSEFI G R. Demand response modeling considering interruptible/curtailable loads and capacity market programs[J]. Applied Energy, 2010, 87(1): 243-250.

[15] 赵洪山,王莹莹,陈松.需求响应对配电网供电可靠性的影响[J].电力系统自动化,2015,39(17):49-55.DOI:10.7500/AEPS20150205007.

ZHAO Hongshan, WANG Yingying, CHEN Song. Impact of demand response on distribution system reliability[J]. Automation of Electric Power Systems, 2015, 39(17): 49-55. DOI: 10.7500/AEPS20150205007.

[16] 张海涛,秦文萍,韩肖清,等.多时间尺度微电网能量管理优化调度方案[J].电网技术,2017,41(5):1533-1540.

ZHANG Haitao, QIN Wenping, HAN Xiaoqing, et al. Multi-time scale optimization scheduling scheme of microgrid energy management[J]. Power System Technology, 2017, 41(5): 1533-1540.

[17] 王成山,李鹏.分布式发电、微网与智能配电网的发展与挑战[J].电力系统自动化,2010,34(2):10-14.

WANG Chengshan, LI Peng. Development and challenges of distributed generation, the micro-grid and smart distribution system[J]. Automation of Electric Power Systems, 2010, 34(2): 10-14.

[18] 尤毅,刘东,于文鹏,等.主动配电网技术及其进展[J].电力系统自动化,2012,36(18):10-16.

YOU Yi, LIU Dong, YU Wenpeng, et al. Technology and its trends of active distribution network[J]. Automation of Electric Power Systems, 2012, 36(18): 10-16.

[19] 秦祯芳,岳顺民,余贻鑫,等.零售端电力市场中的电量电价弹性矩阵[J].电力系统自动化,2004,28(5):16-21.

QIN Zhenfang, YUE Shunmin, YU Yixin, et al. Price elasticity matrix of demand in current retail power market[J]. Automation of Electric Power Systems, 2004, 28(5): 16-21.

[20] FALSAFI H, ZAKARIAZADEH A, JADID S. The role of demand response in single and multi-objective wind-thermal generation scheduling: a stochastic programming[J]. Energy, 2014, 64(1): 853-867.

[21] MOGHADDAM M P, ABDOLLAHI A, RASHIDINEJAD M. Flexible demand response programs modeling in competitive electricity markets[J]. Applied Energy, 2011, 88(9): 3257-3269.

[22] 杨楠,刘涤尘,董开松,等.考虑柔性负荷补偿/激励机制的风电供需侧一体化随机调度方法[J].电力自动化设备,2015,35(2):15-20.

YANG Nan, LIU Dichen, DONG Kaisong, et al. Integrated random scheduling for supply and demand sides of wind power system considering flexible load compensation/incentives[J]. Electric Power Automation Equipment, 2015, 35(2): 15-20.

[23] SANTOS A, MCGUCKIN N, NAKAMOTO H Y, et al. Summary of travel trends: 2009 national household travel survey[R]. 2011.

[24] 比亚迪汽车官方网站.比亚迪E6型纯电动汽车参数[EB/OL].[2017-07-26].http://www.bydauto.com.cn/car-show-e6.html.

[25] 宇通汽车官方网站.E12型天津运行示范数据[EB/OL].[2017-07-10].http://www.yutong.com/zhuanti/yiqikaishi/index.html#page4.

[26] ZHAO J H, WEN F, DONG Z Y, et al. Optimal dispatch of electric vehicles and wind power using enhanced particle swarm optimization[J]. IEEE Transactions on Industrial Informatics, 2012, 8(4): 889-899.

[27] 王司阳.计及电动汽车换电站的微网/配电网双层优化调度研究[D].秦皇岛:燕山大学,2016.