计及需求价格弹性的区域能源中心建模与日前优化调度

陈泽兴, 张勇军, 许志恒, 蔡泽祥, Thanhtung HA

(广东省绿色能源技术重点实验室, 华南理工大学电力学院, 广东省广州市 510640)

0 引言

以能源的分布式开发、多能互补综合利用为核心,加强需求侧管理,实现用户真正参与,推进能源系统削峰填谷、低碳高效,是能源系统发展的必由之路[1-3]。在此背景下,打破现有各供能系统独立规划、设计、运行的模式,实现能源市场化,构建多能流耦合的综合能源系统(integrated energy system,IES)备受关注[4-6]。

IES可抽象看成由多种能源网络实现多个区域能源中心(district energy centre,DEC)的连接[7]。DEC是多能源耦合的区域分布式能源系统,它通过各类能源转换器实现区域内电、热、冷、气等能源之间的交互,供能对象包括商务区、产业园区、微能源网、工业园区、智能楼宇等,具小地块特征。为统一描述DEC中多能流耦合的关系,苏黎世联邦理工学院于2007年首次提出了能量枢纽(energy hub,EH)的建模方法[8],该方法通过耦合矩阵描述DEC的能量分配与转化关系,实现对DEC中多能流的耦合联系的数学建模,并在解决DEC规划、优化运行问题中发挥了重要作用,已成为研究热点[9-10]。

在规划层面,文献[11-13]分别将EH建模方法应用于医院、酒店和居民用户这几类DEC的热电能源供应问题上,并对能源供应/存储设备(如热电联产(CHP)、热锅炉、电池等)的容量进行了优化选择;文献[14]则通过建立含0-1变量的模型,用以确定EH中设备的最优组合;在优化运行层面,文献[15-16]以居民的电热冷供应系统进行EH建模,在满足相应运行约束的条件下,优化各式能源之间的分配转化关系,实现用能成本最小化;文献[17]对EH内设备响应需求侧的灵活性进行分析,在EH优化调度模型中计及了需求侧响应;文献[18-19]还分别增加了新能源、电动汽车等元素,统一于EH建模,并考虑了系统不确定因素对运行的影响。类似基于EH建模的DEC规划、运行方法的研究仍有不少[20-22],但总体看来:

1)基于EH的建模方法,主要用来描述DEC中多能源耦合功率的稳态平衡关系,但大部分文献针对不同DEC的建模需要具体分析,缺乏通用的建模方法,增加了复杂系统的建模难度;文献[7]在研究DEC稳态优化调度时,对DEC通用性建模进行了初探,但由于能量分配系数的引入,使得原本可用线性描述的DEC功率平衡方程非线性化,增加了问题的复杂性。

2)DEC日前优化调度方面,尽管有部分文献考虑负荷的需求侧响应,但需求侧响应能力的表现形式多反映为可平移负荷、可控负荷等[17,23-25],价格特性反映不明显。能源市场管制放松的背景下[26-27],能源价格将发展成为一种控制资源,计及需求价格弹性并以实时/分时能源价格的制定引导需求侧参与系统决策将成为趋势。

基于此,本文首先在EH模型的基础上,以DEC内各设备的连接关系矩阵描述为关键表征量,提出了DEC稳态功率平衡方程通用性建模方法,将DEC功率平衡方程描述为待求变量的线性表达;再者,计及能源负荷需求的价格弹性,提出能源负荷需求的分段线性化建模方法;进一步,考虑能源价格作为一种控制手段,以最大化DEC净收益为目标,建立了DEC日前优化调度模型;最后,通过一个微网型DEC对所提模型进行了验证和算例仿真。

1 DEC稳态功率平衡方程通用线性化建模

基于EH模型的DEC抽象结构如图1所示,描述为输入—输出的二端口网络[8]。本节提出DEC稳态功率平衡方程通用线性化建模,主要反映多能流功率的稳态/准稳态的有功平衡关系,适于DEC日前计划,其“通用性”体现在该建模方法可基于DEC内设备连接关系矩阵的描述获得功率平衡方程,适用于任一DEC,便于计算机编程实现。

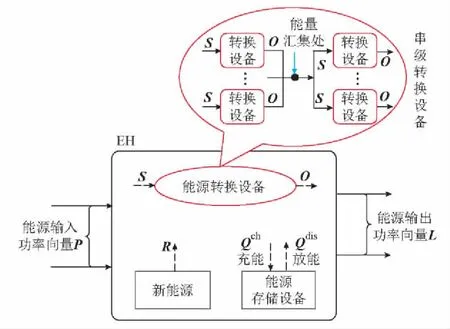
图1 基于EH模型的DEC示意图Fig.1 Diagram of DEC based on EH model

具体地,DEC中M个能源输入功率向量P=[P1,P2,…,Pm,…,PM]T(m=1,2,…,M)表征DEC与上级能源系统的功率交换,N个能源输出功率向量L=[L1,L2,…,Ln,…,LN]T(n=1,2,…,N)表示DEC的负荷。DEC内部包含了能源转换设备(可能组成串级转换设备,具体定义见下文)、能源存储设备、新能源设备等。

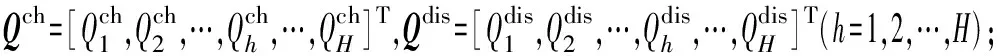
O=ηS

(1)

式中:η=(ηij)I×J为I行J列矩阵,其中ηij为能源转换设备输入端j至输出端i的稳态转换效率[7,9]。

从设备连接关系看,DEC内新能源、能源存储设备可连接于DEC的输入/输出端或各能源转换设备的输入/输出端。因此,当存在新能源及能源存储设备的功率向量R,Qch,Qdis时,可认为是对P,L,O,S的修正。基于此,先对仅含能源转换设备的DEC进行数学建模。

1)端口关联矩阵C

该建模方法中,能量从DEC的输入端到输出端的任一通路都需经过至少一种能源转换设备,若存在某一通路不经过能源转换设备,需自行增加虚拟能源转换设备,并认为转化效率为100%。定义端口关联矩阵C为M+N行I+J列矩阵,表征DEC输入/输出端口与能源转换设备输入/输出端口的连接关系,且C与P,L,O,S的关系为:

(2)

其中,CPO=(cmi)M×I,CPS=(cmj)M×J,CLO=(cni)N×I,CLS=(cnj)N×J为C的分块矩阵,并且

(3)

式中:m端和n端分别指能源输入端口Pm和能源输出端口Ln;i端和j端分别指能源转换设备输出端口Oi及输入端口Sj。

2)串级转换设备端口位置矩阵D

串级转换设备(见图1)由多个能源转换设备组成,是指DEC中的能量经过一个(多个)能源转换设备输出后,汇集输入另一个(多个)能源转换设备中,且在能量汇集处不与DEC输入输出端相连。

假设DEC中有G个串级转换设备,g为其计数变量(g=1,2,…,G),定义G×(I+J)阶矩阵D为串级转换设备端口位置矩阵,且

(4)

式中:DO=(Dgi)G×I和DS=(Dgj)G×J为D的分块矩阵。

对于某串级转换设备g,若在能量汇集处与能源转换设备输出、输入端口i和j相连接,则对应的Dgi和Dgj取1,否则取0,则D与O和S的关系为:

DOO=DSS

(5)

因此,不考虑DEC内新能源和储能时,联立式(1)、式(2)和式(5),消去矩阵O,可得DEC稳态功率平衡方程如式(6)所示。

(6)

(7)

式中:I为M阶单位矩阵。

3)计及新能源、储能的DEC稳态功率平衡方程

定义新能源设备位置矩阵A为I+J+M+N行K列矩阵,储能设备位置矩阵B为I+J+M+N行H列矩阵。将矩阵A和B按I,J,M,N维度进行分块,有

(8)

式中:AO=(Aik)I×K和BO=(Bih)I×H分别表示新能源设备、储能设备与DEC内部各能源转换设备输出端口的关系,若新能源设备k或储能设备h存储/补充能源转换设备输出端口i的能量,对应元素Aik和Bih取值1,否则为0;AS=(Ajk)J×K,AP=(Amk)M×K,AL=(Ank)N×K分别表示新能源设备与各能源转换设备输入端口、DEC输入端、DEC输出端的能量承接关系;BS=(Bjh)J×H,BP=(Bmh)M×H,BL=(Bnh)N×H分别表示储能设备与各能源转换设备输入端口、DEC输入端、DEC输出端的能量承接关系。AS,AP,AL,BS,BP,BL矩阵内元素的取值方式与AO和BO相同。

表1给出了计及新能源、储能设备时,对式(2)和式(5)中的P,L,O,S的修正公式。

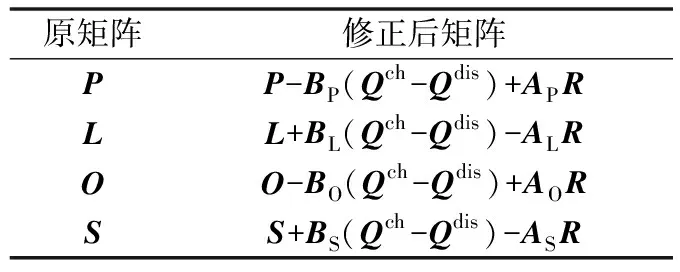
表1 P,L,O,S的修正公式Table 1 Revised formulas of P,L,O,S

因此,考虑新能源和储能设备时,基于表1对式(2)和式(5)的修正,并联立式(1)、式(2)和式(5),可得DEC功率平衡方程如式(9)所示。

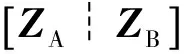
(9)

ZB=

(10)

综上,通过对DEC内设备连接关系矩阵进行描述,即矩阵A,B,C,D,基于式(9)即可列写DEC稳态功率平衡方程,且表达式为线性。该做法简明、清晰且具通用性,当DEC内设备增添删减时只需对A,B,C,D进行修正。

2 需求价格弹性与分段线性化建模

能源负荷需求的价格弹性可表示为能源价格—需求曲线上任一点的切线的斜率[28-30]。能源价格—需求曲线建立在对用户的深入调研之上,以获得用户对能源价格的响应特性为目的,开展数据收集、统计并进行函数拟合[31-33]。本文不对用户需求特性测算方面展开研究,而基于微积分中“以直代曲”的思想,认为所获得的能源价格—需求响应特性数据均可采用分段线性化进行拟合,具体为:由调研分析获得一系列能源价格—需求的有序数对,根据有序数对的变化趋势分成若干组,对每组有序数对用MATLAB中的Curve Fitting工具箱进行线性拟合[34],获得多段分段线性函数,随后判断残差平方和是否满足预设精度,若不满足,则人为调整或增加有序数对分组数,重新进行分段线性拟合,直到残差平方和满足预设精度要求。

能源负荷需求分段线性化的数学模型可统一表示为:对于DEC中第n个能源负荷,在时段t,有

(11)

式中:w(w=1,2,…,W)表示第w段线性函数;W为总分段数;α和β表示线性化拟合参数,为常数,且α即为能源负荷需求的价格弹性;ρ表示能源价格,为变量;δ表示0-1逻辑变量,若δn,t,w取1,则表示能源负荷需求位于第w段线性函数上,反之,若δn,t,w取0则表示能源负荷需求不在第w段线性函数上。对应的分段线性化建模示意图见附录A图A1。

由于能源负荷需求仅可能在某一段分段线性函数上,因此W个逻辑变量δ仅一个取值为1,其余为0。并且,当δn,t,w取0时,对应变量ρn,t,w也可钳制为0而与式(11)保持等价。因此,变量δ和ρ满足:

(12)

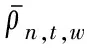
进一步,由式(12)可知:

当δn,t,w=0时,可得:

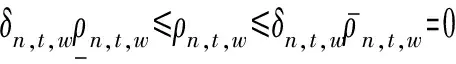
ρn,t,w=0⟹αn,t,wρn,t,wδn,t,w=αn,t,wρn,t,w=0

(13)

当δn,t,w=1时,可得:

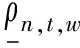
αn,t,wρn,t,wδn,t,w=αn,t,wρn,t,w

(14)

综合式(13)和式(14),则有

αn,t,wρn,t,wδn,t,w=αn,t,wρn,t,w

(15)

同理可得:

βn,t,wρn,t,wδn,t,w=βn,t,wρn,t,w

(16)

基于式(15),可将式(11)关于ρ和δ的非线性函数转化为关于ρ和δ的线性表达,如式(17)所示,从而保持功率平衡方程的表达式为线性,进而简化模型。

(17)

综上,能源负荷需求的分段线性化建模由式(17)的线性表达式及式(12)的线性约束构成。

此外,从需求法则看,能源负荷需求一般与价格成反向变动[29,33],因此α一般为负值。习惯上研究其绝对值,并认为|α|越小,能源负荷需求的价格弹性越低,反之,则越大。

3 DEC日前优化调度模型

以DEC净收益最大化为目标,计及能源负荷需求的价格弹性,建立DEC日前优化调度模型。模型的决策变量包括:DEC能源输入端功率向量P、DEC内设备功率向量S,R,Qch,Qdis以及式(12)和式(17)中负荷模型涉及的变量ρn,t,w和δn,t,w。

3.1 目标函数

目标函数如下:

(18)

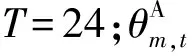
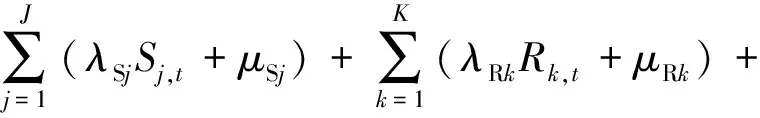
(19)

式中:λS和μS表示能源转换设备的运行成本系数;λR和μR表示新能源运行成本系数;λQ和μQ表示储能设备的运行成本系数。

将式(12)和式(17)所表示的能源负荷需求模型代入式(18),并结合式(16),则目标函数可表示为决策变量的二次式,即

(20)

3.2 约束条件

DEC运行的约束条件主要包括:式(9)的功率平衡约束、式(12)的能源负荷价格及逻辑变量约束以及能源转换设备、储能设备、新能源设备的运行约束,与上级能源系统交换功率的约束,阐述如下。

1)能源转换设备运行约束

能源转换设备主要实现不同能源形式之间的转化和耦合,如电解槽、燃气轮机、电锅炉等;其运行约束主要为设备的出力约束和爬坡约束。对于任一能源转换设备功率,均有

(21)

(22)

式中:上标max和min分别表示对应变量的上、下限,下同;Sup和Sdown分别表示设备爬坡上升、下降出力限值。

2)储能设备运行约束

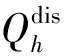
(23)

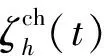
3)新能源设备运行约束

新能源,如风电、光伏发电等,其调度主要结合预测出力,满足下述约束:

(24)

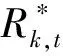
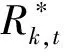
(25)

式(25)为带区间数约束条件,引入置信水平χ将其转化为一般的实数约束条件,见式(26)[35-36]。

(26)

其中,置信水平χ表征区间约束的满意程度,即区间约束式(25)的可能度,取值[0,1]。

4)与上级能源系统功率交换约束

(27)

综上,所建立的计及需求价格弹性的DEC日前优化调度模型为混合整数二次规划模型,本文采用GAMS调用CPLEX进行求解[37]。

4 算例分析

本文基于文献[25]的微网型能源集线器,对其进行适当拓展,构建多种能源形式(电、气、热等)的微网型DEC模型如图2所示。

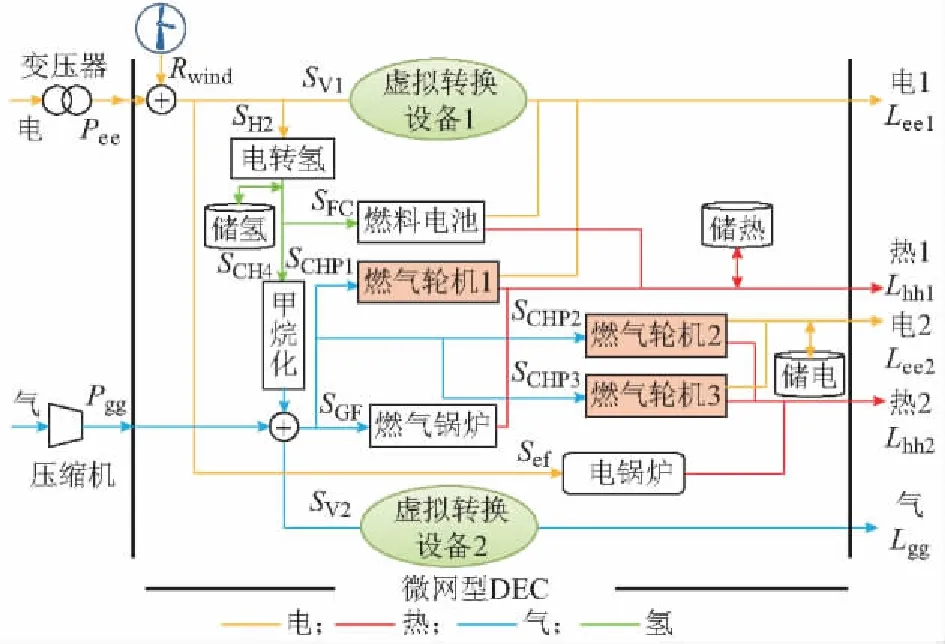
图2 微网型DEC模型图Fig.2 Structure of microgrid-type DEC

基于第1节所提的功率平衡方程通用性建模方法,DEC输入、输出端口主要变量表示如下:P=[Pee,Pgg]T,L=[Lee1,Lhh1,Lee2,Lhh2,Lgg]T,其中下标ee表示电能,hh分别表示热能,gg表示天然气能。且由拓扑结构可知,电能从DEC输入端到Lee1、天然气DEC输入端到Lgg均存在一通路不经过能源转换器,故增加虚拟转换设备。如图2所示。进一步,通过确定端口关联矩阵C,串级转换设备端口位置矩阵D(图2含一个串级转换设备,由电转氢设备、甲烷化设备及燃料电池组成),以及在含新能源、储能设备的情况下进行矩阵修正,可细化式(9)相关矩阵为(具体推导过程见附录B):

上述矩阵中,ηH2,ηmc,ηfce,ηfct分别为电转氢、甲烷化、燃料电池转电及转热效率;ηche1,ηche2,ηche3及ηcht1,ηcht2,ηcht3分别为第1,2,3台燃气轮机气转电效率及气转热效率;ηgf和ηef分别为燃气锅炉和电锅炉效率,设备效率取值详见附录C表C1;ηv1和ηv2分别为两个虚拟转换设备的转换效率,取100%。而S的下标中,H2,CH4,FC,CHP,GF,ef,V分别指电转氢设备、甲烷化设备、燃料电池、燃气轮机、燃气锅炉、电锅炉、虚拟转换设备。Qch与Qdis的下标sH,sh,se分别指储氢、储热、储电设备;Rwind为风力发电机出力。

附录C表C2至C4给出了DEC内设备的相关运行参数。附录D图D1给出了参考价格100美元/(MW·h)下的电负荷Lee1和Lee2,热负荷Lhh1和Lhh2,参考价格80美元/(MW·h)下的气负荷Lgg及风电预测曲线;图D2给出了DEC从外部购入的电和天然气价格曲线。本文考虑风机归DEC调度运行者所有,故风电购入成本取0,风电预测区间取预测值的±20%。

4.1 需求价格弹性下的DEC优化调度结果

基于图2的微网型DEC模型,取χ=0.5,进行日前优化调度计算。能源价格—需求特性取某城区的统计分析结果,并预设残差平方和精度为小于0.1进行分段线性拟合,拟合后弹性系数如附录D表D1。

结合图2的拓扑图及DEC内各设备优化调度结果表明(设备出力如附录D图D3所示),在电负荷Lee1处于低谷、风电富余时(如1～8 h,21～24 h),Lee1由风电满足;同时,电转氢、储氢、甲烷化设备动作以吸收富余且廉价的风电,储存备用或以天然气形式传输。而在Lee1高峰时段,风电、释放氢气用以燃料电池发电仍不满足Lee1的需求,此时,由于购气价相比购电价便宜,则燃气轮机1工作供电。由于燃气轮机容量约束的存在,在Lee1较高的某些时段(如17～19 h),仍需通过外购较高电价的电力用以满足Lee1的需求。

而热负荷Lhh1主要由燃气轮机1和燃气锅炉提供并形成互补,而受容量约束影响,燃料电池仅为Lhh1提供少量热。与燃气轮机1相比,燃气锅炉产热效率高,故热负荷本应主要由燃气锅炉提供,但当Lee1需燃气轮机1供给时,可将余热供给Lhh1或储存起来备用,受此约束则无须开燃气锅炉;而当燃气轮机1停机或供热不足时,燃气锅炉启动供热。气负荷Lgg的来源途径有:外购天然气或电转氢并甲烷化。而当风电不足(如9～20 h)时,电转氢及甲烷化设备停止运行,Lgg由外购天然气满足。这一方面是因为此时风电用以满足Lee1的部分需求,而不经电转氢并甲烷化带来额外的损耗;另一方面是因为外购天然气相比外购电便宜。

此外,燃气轮机2和3、电储能及电锅炉三者互补满足Lee2和Lhh2的需求,由于大部分时段购气比购电便宜,则燃气轮机2和3出力较大,若燃气轮机所产的余热不满足Lhh2,则需开启电锅炉供热。

上述基于仿真结果阐述了在既定负荷需求下,如何充分利用DEC内的设备,实现能源购置成本最小化以实现净收益的最大化。而图3给出了能源负荷的最优定价策略,是从负荷侧的角度进一步挖掘系统的优化潜力来最大化DEC净收益。

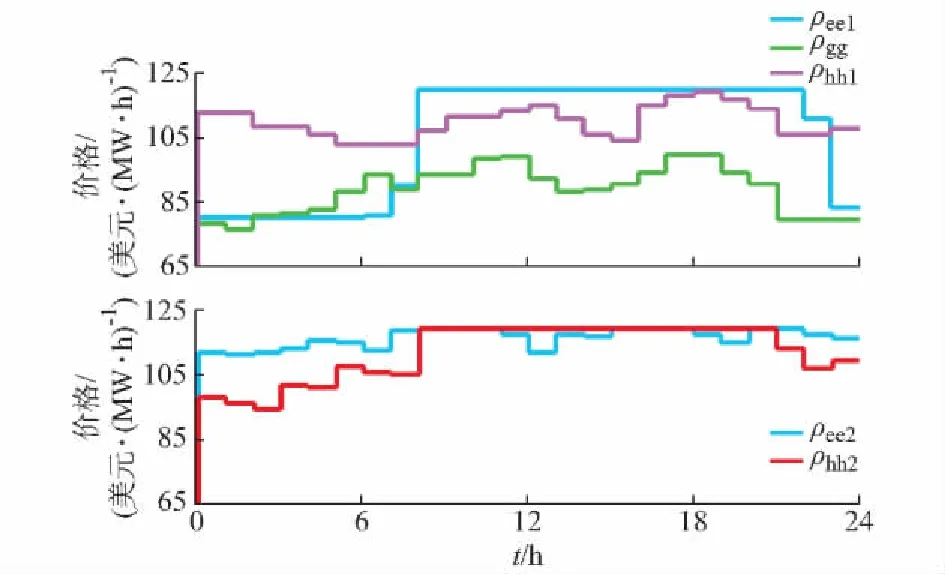
图3 最优实时能源价格Fig.3 Optimal price of real-time purchasing energy

由价格弹性的特性可知,抬高能源售价会使负荷需求降低,反之,降低能源售价将增加负荷需求。由于售能收益为售价与需求量的乘积,在售价与需求量成反比的关系下,售能收益最大化是售价与需求量相互作用的结果。从图3的结果看,当能源售价未逼近上限时,能源售价的变化趋势与参考负荷(即附录D图D1)变化趋势相同,即当负荷需求较低时,可通过降低能源售价,提升需求以获得更大售能收益;反之,当负荷需求较高,适当提升能源售价,降低需求,也有利于售能收益的提高。

4.2 不同需求价格弹性对负荷特性的影响

为分析不同需求价格弹性对最优定价及负荷曲线的影响,本节设置5个具有不同需求价格弹性的场景进行对比分析。其中,Case 1取4.1节中所用的需求价格弹性;Case 2和Case 3的需求价格弹性分别较Case 1低、高;Case 4的需求价格弹性设为0；Case 5不考虑能源价格的调控。各场景的具体参数详见附录D表D2。本节中χ均取0.5。

表2给出了不同场景下各能源负荷方差、峰谷差、DEC收益及风电消纳比例,用以反映价格对负荷特性的影响。由数据可知,相比不考虑价格调控(Case 5),将负荷能源作为一种可控资源后(Case 1至3),DEC的净收益将有所提高,同时有利于减少负荷方差、峰谷差,并提高风电消纳比例。Case 4为特例,该场景的价格弹性系数为0,因此其尽管考虑价格调控,但仍未能改变负荷特性,进而其负荷方差、峰谷差、风电消纳比例与Case 5相同,此时,DEC制定的能源价格逼上限以实现净收益最大化。

而随着价格弹性的增大(Case 4→Case 2→Case 1→Case 3),通过能源价格改变负荷特性的能力也随之增大,即随着价格弹性的增大,负荷方差及峰谷差随之减少。并且,在价格弹性的驱动下,风电富余而电负荷低谷时段,还可通过价格调控推进廉价风电的消纳,提升新能源消纳比例。

表2 不同场景的优化结果对比Table 2 Comparison of optimization results in different cases

4.3 风电预测区间置信水平χ对优化结果的影响

本文将新能源(风电)的预测值的不确定性以区间的形式表示,并通过引入置信水平χ表征区间约束的满意程度,如式(25)和式(26)所示,为分析置信水平χ对优化结果的影响,以4.2节中Case 1和Case 5为例,分别代表有无计及能源负荷价格调控,考察χ在0～1变化时对优化结果的影响。

仿真结果表明(具体数据见附录D表D3),随着χ的增加,DEC从上级能源系统购入的能量(电/气)随之增加,而DEC净收益则随之减少。实际上,χ值从工程实际意义可表示为调度者对风电预测区间所持的态度。χ值越大,区间约束的可能度越大,此时,调度者持保守态度,从风电出力最坏(最小)的情况出发,进行日前计划,需从外部购置更多的能源,这将使得调度净收益减少并可能造成风电利用率下降,但调度风险小,负荷需求在极端情况下仍能满足。而随着χ值变小,在日前调度净收益增大之余,也增大了调度的风险,在日前计划实施的过程中可能造成负荷需求无法满足进而需上层能源网络提供支撑以实现供需平衡。实际决策中,调度者可以根据实际偏好做出乐观或保守的估计,进行调度方案求解。

5 结语

本文立足能源市场管制放松的背景,考虑能源负荷价格参与调控,计及负荷需求的价格弹性,开展了DEC的建模与日前优化调度方法研究,主要结论如下。

1)基于各设备连接关系矩阵描述的DEC稳态功率平衡方程建模方法,简明、清晰,对复杂系统的建模具有通用性,便于计算机编程实现。

2)基于“以直代曲”的思想,所建立的考虑价格弹性的负荷需求分段线性化模型具有通用性;而以0-1变量的引入及线性约束的构建将分段线性化模型统一描述,保持了负荷模型的线性表达,降低了模型复杂性。

3)能源负荷价格参与调控下,DEC可充分利用负荷需求的价格弹性,在最大化其净收益之余,也有利于负荷特性的改善,如减少负荷方差和峰谷差等,且价格弹性越高,负荷特性的改善程度越好;此外,利用负荷的价格弹性特性引导负荷参与调控,还有助于新能源消纳能力的提升,实现系统优化潜力的进一步挖掘。

4)引入新能源预测区间置信水平χ衡量调度的经济性与风险程度。χ越大,调度风险越小但经济性差;反之,χ越小,调度风险越大但经济性好,调度者可根据实际偏好做出乐观或保守的估计,进行DEC日前优化调度,增加系统决策的柔性。

5)本文对DEC的建模主要反映多能流功率的稳态/准稳态的有功平衡关系,适用于DEC做日前计划。下一步可针对DEC内多能源不同时间尺度动态特性建模及非稳态运行优化问题开展研究。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参考文献

[1] HUANG A Q, CROW M L, HEYDT G T, et al. The future renewable electric energy delivery and management (FREEDM) system: the energy internet[J]. Proceedings of the IEEE, 2011, 99(1): 133-148.

[2] 李立浧,张勇军,陈泽兴,等.智能电网与能源网融合的模式及其发展前景[J].电力系统自动化,2016,40(11):1-9.DOI:10.7500/AEPS20150912002.

LI Licheng, ZHANG Yongjun, CHEN Zexing, et al. Merger between smart grid and energy-net: mode and development prospects[J]. Automation of Electric Power Systems, 2016, 40(11): 1-9. DOI: 10.7500/AEPS20150912002.

[3] KRAUSE T, ANDERSSON G, FROEHLICH K, et al. Multiple-energy carriers: modeling of production, delivery, and consumption[J]. Proceedings of the IEEE, 2011, 99(1): 15-27.

[4] WU J, YAN J, JIA H, et al. Integrated energy systems[J]. Applied Energy, 2016, 167: 155-157.

[5] 李洋,吴鸣,周海明,等.基于全能流模型的区域多能源系统若干问题探讨[J].电网技术,2015,39(8):2230-2237.

LI Yang, WU Ming, ZHOU Haiming, et al. Study on some key problems related to regional multi energy system based on universal flow model[J]. Power System Technology, 2015, 39(8): 2230-2237.

[6] 贾宏杰,王丹,徐宪东,等.区域综合能源系统若干问题研究[J].电力系统自动化,2015,39(7):198-207.DOI:10.7500/AEPS20141009011.

JIA Hongjie, WANG Dan, XU Xiandong, et al. Research on some key problems related to integrated energy systems[J]. Automation of Electric Power Systems, 2015, 39(7): 198-207. DOI: 10.7500/AEPS20141009011.

[7] 王业磊,赵俊华,文福拴,等.具有电转气功能的多能源系统的市场均衡分析[J].电力系统自动化,2015,39(21):1-10.DOI:10.7500/AEPS20150623001.

WANG Yelei, ZHAO Junhua, WEN Fushuan, et al. Market equilibrium of multi-energy system with power-to-gas functions[J]. Automation of Electric Power Systems, 2015, 39(21): 1-10. DOI: 10.7500/AEPS20150623001.

[8] GEIDL M, KOEPPEL G, FAVRE-PERROD P, et al. Energy hubs for the future[J]. IEEE Power & Energy Magazine, 2006, 5(1): 24-30.

[9] 王毅,张宁,康重庆.能源互联网中能量枢纽的优化规划与运行研究综述及展望[J].中国电机工程学报,2015,35(22):5669-5681.

WANG Yi, ZHANG Ning, KANG Chongqing. Review and prospect of optimal planning and operation of energy hub in energy internet[J]. Proceedings of the CSEE, 2015, 35(22): 5669-5681.

[10] ZHANG Xiaping, SHAHIDEHPOUR M, ALABDULWAHAB A A. Optimal expansion planning of energy hub with multiple energy infrastructures[J]. IEEE Transactions on Smart Grid, 2015, 6(5): 2302-2311.

[11] BAHRAMI S, SAFE F. A financial approach to evaluate an optimized combined cooling, heat and power system[J]. Energy & Power Engineering, 2013, 5(5): 352-362.

[12] SHEIKHI A, RANJBAR A M, SAFE F. A novel method to determine the best size of CHP for an energy hub system[C]// International Conference on Electric Power and Energy Conversion Systems, November 15-17, 2011, Sharjah, United Arab Emirates: 1-7.

[13] REN Hongbo, GAO Weijun, RUAN Yingjun. Optimal sizing for residential CHP system[J]. Applied Thermal Engineering, 2008, 28(5/6): 514-523.

[14] GEIDL M, ANDERSSON G. Optimal coupling of energy infrastructures[C]// 2007 IEEE Lausanne Power Tech, July 1-5, 2007, Lausanne, Switzerland: 1398-1403.

[15] BOZCHALUI M C, HASHMI S A, HASSEN H, et al. Optimal operation of residential energy hubs in smart grids[J]. IEEE Transactions on Smart Grid, 2012, 3(4): 1755-1766.

[16] MOGHADDAM I G, SANIEI M, MASHHOUR E. A comprehensive model for self-scheduling an energy hub to supply cooling, heating and electrical demands of a building[J]. Energy, 2016, 94: 157-170.

[17] MANCARELLA P, CHICCO G. Real-time demand response from energy shifting in distributed multi-generation[J]. IEEE Transactions on Smart Grid, 2013, 4(4): 1928-1938.

[18] PAZOUKI S, HAGHIFAM M R, MOSER A. Uncertainty modeling in optimal operation of energy hub in presence of wind, storage and demand response[J]. International Journal of Electrical Power & Energy Systems, 2014, 61: 335-345.

[19] RASTEGAR M, FOTUHI-FIRUZABAD M, LEHTONEN M. Home load management in a residential energy hub[J]. Electric Power Systems Research, 2015, 119: 322-328.

[20] SALIMI M, GHASEMI H, ADELPOUR M A. Optimal planning of energy hubs in interconnected energy systems: a case study for natural gas and electricity[J]. IET Generation Transmission & Distribution, 2015, 9(8): 695-707.

[21] 王珺,顾伟,张成龙,等.智能社区综合能源优化管理研究[J].电力系统保护与控制,2017,45(1):89-97.

WANG Jun, GU Wei, ZHANG Chenglong, et al. Research on integrated energy management for smart community[J]. Power System Protection and Control, 2017, 45(1): 89-97.

[22] HA T, ZHANG Y, THANG V V, et al. Energy hub modeling to minimize residential energy costs considering solar energy and BESS[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(3): 389-399.

[23] BAHRAMI S, SHEIKHI A. From demand response in smart grid toward integrated demand response in smart energy hub[J]. IEEE Transactions on Smart Grid, 2016, 7(2): 650-658.

[24] 李东东,徐连连,刘翔,等.考虑可削减负荷参与的含风光储微网经济优化调度[J].电力系统保护与控制,2017,45(2):35-41.

LI Dongdong, XU Lianlian, LIU Xiang, et al. Optimal dispatching of microgrid considering the participation of reducible loads, distributed generators (DG) and energy storage units[J]. Power System Protection and Control, 2017, 45(2): 35-41.

[25] 陈沼宇,王丹,贾宏杰,等.考虑P2G多源储能型微网日前最优经济调度策略研究[J].中国电机工程学报,2017,37(11):3067-3077.

CHEN Zhaoyu, WANG Dan, JIA Hongjie, et al. Research on optimal day-ahead economic dispatching strategy for micro-grid considering P2G and multi-source energy storage system[J]. Proceedings of the CSEE, 2017, 37(11): 3067-3077.

[26] 孙宏斌,郭庆来,潘昭光.能源互联网:理念、架构与前沿展望[J].电力系统自动化,2015,39(19):1-8.DOI:10.7500/AEPS20150701007.

SUN Hongbin, GUO Qinglai, PAN Zhaoguang. Energy Internet: concept,architecture and frontier outlook[J]. Automation of Electric Power Systems, 2015, 39(19): 1-8. DOI: 10.7500/AEPS20150701007.

[27] KARTHIKEYAN S P, RAGLEND I J, KOTHARI D P. A review on market power in deregulated electricity market[J]. International Journal of Electrical Power & Energy Systems, 2013, 48: 139-147.

[28] KIRSCHEN D S, STRBAC G, CUMPERAYOT P, et al. Factoring the elasticity of demand in electricity prices[J]. IEEE Transactions on Power Systems, 2000, 15(2): 612-617.

[29] FAN Shu, HYNDMAN R J. The price elasticity of electricity demand in South Australia[J]. Energy Policy, 2011, 39(6): 3709-3719.

[30] 黄永皓,康重庆,李晖,等.用电需求曲线建模及其应用[J].电工电能新技术,2004,23(1):29-33.

HUANG Yonghao, KANG Chongqing, LI Hui, et al. The model of electricity demand curve and its applications[J]. Advanced Technology of Electrical Engineering and Energy, 2004, 23(1): 29-33.

[31] BJØRNER T B, TOGEBY M, JENSEN H H. Industrial companies’ demand for electricity: evidence from a micropanel[J]. Energy Economics, 2001, 23(5): 595-617.

[32] BOOGEN N, DATTA S, FILIPPINI M. Going beyond tradition: estimating residential electricity demand using an appliance index and energy services [J]. SSRN Electronic Journal, 2014, 61: 381-386.

[33] POURAZARM E, COORAY A. Estimating and forecasting residential electricity demand in Iran[J]. Economic Modelling, 2013, 35(5): 546-558.

[34] 田垅,刘宗田.最小二乘法分段直线拟合[J].计算机科学,2012,39(增刊1):482-484.

TIAN Long, LIU Zongtian. Least-squares method piecewise linear fitting[J]. Computer Science, 2012, 39(Supplement 1): 482-484.

[35] 刘志涛,李炜.区间线性规划的最优解[J].杭州电子科技大学学报,2012,32(2):70-72.

LIU Zhitao, LI Wei. The optimal solution of interval linear programming[J]. Journal of Hangzhou Dianzi University, 2012, 32(2): 70-72.

[36] 达庆利,刘新旺.区间数线性规划及其满意解[J].系统工程理论与实践,1999,19(4):3-7.

DA Qingli, LIU Xinwang. Interval number linear programming and its satisfactory solution[J]. Systems Engineering—Theory & Practice, 1999, 19(4): 3-7.

[37] SURHONE L M, TENNOE M T, HENSSONOW S F. CPLEX[M]. Betascript Publishing: Saarbrücken, Germany, 2010.