输出并联双有源全桥DC-DC变换器虚拟功率均衡控制方法

安 峰, 宋文胜, 杨柯欣, 冯晓云

(西南交通大学电气工程学院, 四川省成都市 610031)

0 引言

随着电力电子技术的发展,电力系统电力电子化成为未来智能电网的主要发展趋势[1]。现有电力系统使用的工频变压器,因其体积庞大、易造成环境污染,且同时不具备对电压、电流的综合控制功能等缺点[2-3],直接影响了未来智能电网的供电质量。因此,研究高效节能的电力电子变压器(power electronic transformer,PET)意义重大[4]。

PET主要由级联多电平整流器(cascaded H-bridge,CHB)和双有源全桥(dual active bridge,DAB)DC/DC变换器及逆变器组成[5-6]。本文重点对其中的输出端并联DAB DC/DC变换器开展研究[7-11]。

对于模块化结构的PET,其最基本的运行原则是各模块的传输功率均分。在实际应用中,由于各模块主电路参数存在差异,系统不可避免地存在传输功率不均衡问题[12-13]。PET的功率均分策略可以分为两种[14]:①CHB控制中间直流侧电压平衡,DAB控制传输功率平衡,此时DAB可以等效为输入独立输出并联(input independent output parallel,IIOP)拓扑结构;②CHB各模块使用相同的移相调制波,即不控制中间直流侧平衡,DAB控制输入电压平衡,此时DAB可以等效为输入串联输出并联(input series output parallel,ISOP)拓扑结构。

文献[15]针对PET提出了一种功率均衡方法,通过采样各模块的电感电流和输入电压,计算各模块的传输功率,并与参考功率进行比较以实现功率均分。该方法虽然结构简单,但需要增加电流传感器采样高频电感电流,增加了系统成本。文献[16]针对PET提出了一种无电流传感器功率均分方法,通过dq解耦控制实现CHB单位功率因数运行,以dq解耦控制中用于控制直流侧电压平衡的动态有功分量为控制目标,通过调节DAB控制各模块的动态有功分量相等,实现传输功率均分。文献[17]建立了针对单个DAB、带有输出电压闭环的输出并联DAB,以及带有输入电压均衡的输出并联DAB三种数学模型,并提出一种简单的功率均分控制方法,通过调节DAB中的相移量来控制输入电压平衡。然而文中并没有详细分析CHB控制策略对于DAB的影响。此外,该算法中变换器的功率控制仅通过比例—积分(PI)控制器来实现,其动态响应较慢。

对于输出并联DAB变换器,其动态响应尤为重要[18]。文献[19]建立了DAB变换器的线性动态谐波模型,以此来设计对于负载突变具有快速响应能力的自适应PI控制器。但该方法中模型建立较为复杂,不适于多模块推广。文献[20]针对DAB提出一种功率模型和PI控制相结合的混合算法,但控制算法中包含负载参数,可移植性差。文献[21]借鉴直接功率控制思想[22-23],提出了一种基于单相移的虚拟功率控制方法。然而该方法在其他相移控制中的推广及在多个模块中的应用还有待研究。纵观现有文献,适用于多模块DAB变换器且具有快速动态响应的功率均分控制方法鲜有报道。

本文以PET中输出并联DAB变换器为研究对象,首先分析了DAB的功率特性。然后针对输出并联DAB中存在的传输功率不均衡及动态响应慢的问题,提出了一种虚拟功率均衡控制(virtual power balance control,VPBC)方法,并基于该方法分析了PET中两种典型控制方法对于输出并联DAB控制策略的影响。最后,基于三单元输出并联DAB实验平台,以文献[17]所提出的输入电容电压平衡控制(voltage balance control,VBC)为参考,进行了对比实验研究。

1 DAB式DC-DC变换器

DAB式DC-DC变换器的电路拓扑如图1所示。

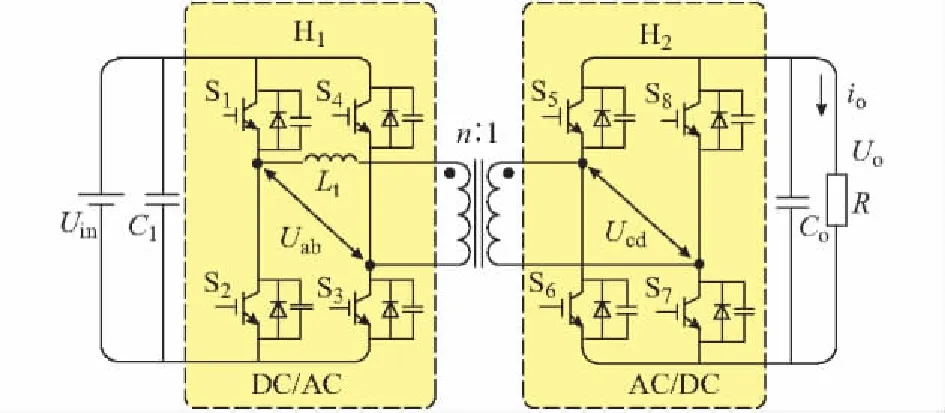
图1 DAB式DC-DC变换器拓扑Fig.1 Topology of DAB DC-DC converter

图1中,DAB式DC-DC变换器由两个H桥和一个中—高频变压器组成。其中,C1为变换器的输入侧支撑电容;Co为变换器的输出侧滤波电容;Lt为辅助电感,其和变压器漏感一起构成了变换器的能量传输元件;中—高频变压器的变比为n∶1;R为DAB变换器的等效负载电阻;Uin和Uo分别为输入电压和输出电压;Uab和Ucd分别为两个H桥的输出电压。

在DAB式DC-DC变换器的工作过程中,两侧H桥的开关频率相同,每个H桥中的对角开关管轮流导通,导通角为180°,这样两个全桥逆变输出的电压Uab和Ucd便是占空比为50%的方波电压。当Uab的相位超前Ucd时,能量正向传输,即从Uin到Uo;反之,能量反向传输。因此,通过控制两个方波电压之间的相角,就可以控制功率传输的大小和方向。传统相移控制的电压电流波形如附录A图A1所示。

附录A图A1中,Ts为开关周期的一半,即Ts=1/(2fs);D表示Uab和Ucd之间的相移量。因此稳态时,DAB的传输功率与相移量之间的关系可以表示为[8]：

(1)

由式(1)可知,当D=0.5时,传输功率达到最大。此外,DAB的输出功率可以表示为Po=UoIo,代入式(1)可得：

(2)

同时可以得到DAB的输出电压表示为：

(3)

由式(2)和式(3)可知,在理想情况下,对于一个主电路参数(不包括负载电阻)确定的DAB电路,任意给定一相移量,其输出的电流值是确定的;而输出的电压除了取决于变换器本身,同时还取决于负载电阻的大小。

对于N个输出并联的DAB,通常使用基准相移角互差360°/N的方波脉冲来分别控制这N个模块,这样不仅可以最大限度地减小输出电压的纹波脉动,而且可以提高输出电压纹波的频率,使得输出侧滤波电容最小化[13]。对于N个模块的输出端并联DAB,此时的输出电压可以表示为:

Uo=(io1+io2+…+ioN)R

(4)

式中：ioi为第i个模块的输出电流。

输出端并联DAB的输出功率为各DAB模块的传输功率之和。此时,第i个DAB模块的输出功率可以表示为：

Pi=Uoioii=1,2,…,N

(5)

2 输出端并联DAB的虚拟功率均衡控制

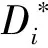
(6)

式中：Lti和Uini分别为第i个模块的辅助电感和输入电压。

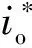
(7)

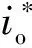
(8)

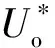
将式(8)代入式(7)可得：

(9)

由式(1)可得,第i个模块的实际传输功率为：

(10)

式中：Di为第i个模块的实际相移量。

为了使得第i个模块的实际传输功率与虚拟功率相等,即满足Poi=Pvi,可求得第i个模块的相移量为：

(11)

其中虚拟电压Uv满足：

(12)

3 CHB控制策略对于DAB的影响分析

3.1 CHB控制直流侧电压平衡

当CHB控制中间直流侧电压平衡时,每个脉宽调制(PWM)整流器会在公共调制信号的基础上，施加一个动态的调制信号以控制输出侧的电压均衡。此时,在不超过CHB可调制范围的前提下,对于DAB来说,其等效为IIOP的拓扑结构,如附录A图A2所示。

对于IIOP连接的DAB,由式(5)可知,各模块的输出功率之比即为输出电流之比,即满足

Po1∶Po2∶…∶PoN=io1∶io2∶…∶ioN

(13)

此时控制各个模块的功率均分可以等效为控制各个模块的输出均流。需要注意的是,这种控制策略下的中间直流侧电压平衡并不意味着功率均衡。这是由于各个模块的输入端是等效独立的,其输入电流不一定相等。

假设变换器的控制策略为虚拟功率均衡控制,且已经达到稳态,则DAB各个模块满足输出电流均等。此时,级联整流器第2个模块(CHB2)由于受到扰动信号而使得后级的输出端并联DAB的第2个模块(DAB2)输入电压下降,即Uin2下降,由式(2)可知,DAB2的输出电流减小,使得DAB2的输出电流小于其他模块的输出电流。为了保证输出电压的稳定及各模块输出电流均分,DAB2的调节器工作,由式(11)可知,DAB2的相移量将增大,使得其输出电流增大,直至变换器进入新的稳态。

由此可知,虚拟功率均衡控制不仅对输出电压的变化具有调节能力;同时,对于输入电压的变化也能达到快速响应。

3.2 CHB不控制直流侧电压平衡

当CHB不控制中间直流侧电压平衡时,即每个PWM整流器使用相同的移相调制波进行调制时,中间级的DAB可以等效为ISOP的拓扑结构,如附录A图A3所示。

在ISOP连接的DAB中,由于各个模块的输入电流相等,其输入功率之比即为输入电压之比,即满足下式：

Pin1∶Pin2∶…∶PinN=Uin1∶Uin2∶…∶UinN

(14)

而变换器的输入功率与输出功率满足:

Pini=ηiPoi

(15)

式中：ηi为第i个DAB的效率。

结合式(13),假设各个DAB模块的效率基本一致,则只需控制每个DAB的输入电压相等即可控制DAB输出均流。

对于ISOP连接的DAB,理想情况下,每个DAB模块可以等效为一个电流源。当作用于各个模块的开关频率和相移量相同时,由于每个模块的主电路参数不完全一致,导致其等效输入阻抗不同,各个模块的输入电压将会发生偏离,最终只有一个模块承受直流侧输入电压。然而在实际电路中,即使各个模块的电路参数不一致,仍然会存在一个稳定工作点,这是因为DAB并不是和理想电流源完全等效。

结合附录A图A3从电路的角度分析,在开环状态下,假设作用于DAB1和DAB2的开关频率和相移量相同, DAB2中的辅助电感参数小于DAB1中的辅助电感参数,在初始时刻Uin1=Uin2,此时由式(1)可知,模块DAB2的传输功率大于模块DAB1,由式(5)可得Iin2>Iin1,则分压电容C2的电流IC2=Iin1-Iin2<0,使得Uin2下降,Uin1上升;同时,由于变换器输入电压的变化,导致Iin1增大和Iin2减小,直至达到新的平衡。由此可知,在开环状态下,对于等效ISOP连接的DAB变换器,辅助电感参数大的模块输入电压高,辅助电感参数小的模块输入电压低。

在闭环状态下,假设变换器的控制策略为VPBC,且已经达到稳态,则DAB各个模块满足输出电流均等。这时DAB2的输入电压由于扰动信号而下降,即Uin2下降。DAB2的调节器工作,由式(11)可知,作用于DAB2的相移量增大,Iin2增大,那么分压电容C2的电流IC2=Iin1-Iin2<0,使得Uin2下降,形成正反馈;同时,DAB2输入电压的下降导致其他模块的输入电压升高,以DAB1为例,由于Uin1升高,作用于DAB1的相移量减小,Iin1较小,那么分压电容C1的电流IC1=Iin-Iin1>0,导致DAB1的输入电压进一步升高,形成正反馈。

由此可知,当DAB1的输入电压因为扰动而下降时,此时控制器需要减小DAB1的相移量以使其电压恢复。这一点和第1种控制策略恰好相反,因此不会存在一种控制策略使得其对于PET中DAB模块的控制在两种控制方案中都适用,因为如果其中一个对于输入电压是负反馈,另一个必然是正反馈。

为了使得VPBC策略同样适用于等效ISOP连接的DAB变换器,使用各个模块输入电压的均值替代相移角优化计算模型(式(11))中的实际输入电压,以此来避免控制电路中的正反馈。因为如果存在扰动使得一个模块的输入电压下降,则必然存在其他模块的输入电压升高,因此计算出的各个模块输入电压的均值基本不变。同时结合PI控制器,将均值电压与各个模块实际输入电压的差值进行PI计算,生成相移角动态调节分量控制中间直流侧电压平衡,进而控制传输功率均分,同时加快动态响应速度。

基于PET的并联DAB的VPBC策略控制框图如图2所示。

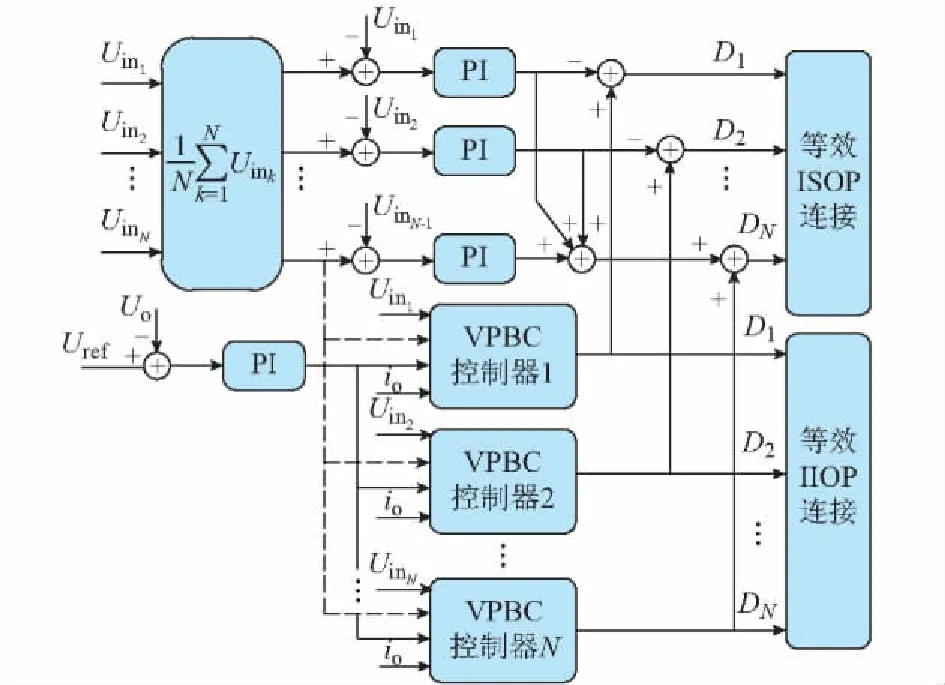
图2 VPBC策略控制框图Fig.2 Block diagram of virtual power balance control strategy

4 实验结果及分析

为了验证本文所提出的用于PET中输出并联DAB变换器VPBC策略的正确性和有效性,搭建了基于TMS320F28335+FPGA_6SLX45为控制器的三模块输出并联DAB的实验平台,其参数如附录A表A1所示。

三模块DAB小型实验样机如附录A图A4所示。在主控制系统中,现场可编程门阵列(FPGA)首先读取AD7606采样数据,然后通过其内部的虚拟双端口随机存储内存(RAM)传输至数字信号处理器(DSP),DSP使用采样数据进行数值运算,而后将运算结果再次传输至FPGA,最终由FPGA发送驱动信号。

为了进一步体现所提算法的有效性,以文献[17]中所提出的VBC策略为参考,进行对比实验研究。文献[17]中所提出的控制算法是CHB不控制中间直流侧电压平衡,而通过DAB来控制输入电容电压平衡以此实现传输功率均分,其控制框图如附录A图A5所示。

4.1 等效ISOP连接DAB实验

当输入电压为150 V(每个DAB模块的等效输入电压为50 V),闭环控制输出电压40 V,负载电阻由15 Ω切换到10 Ω后切回,且不使用功率均衡控制策略时,对于等效ISOP连接的DAB模块,其各个模块的输入电压变化如附录A图A6所示。从图中可以看出,由于各个模块的辅助电感参数不一致,导致其输入电压不均等,即传输功率不均等。且随着负载的加重,各个模块的电压不均衡程度也相应加重。电感参数值大的模块输入电压相对较高,这点与理论分析一致。

图3给出了负载突增时(即负载电阻由15 Ω切换到10 Ω),在VBC与VPBC控制策略下的电压电流实验波形。由图3可知,采用VBC策略时,变换器的动态响应时间为143 ms,输出电压的跌落约为6.4 V。而在VPBC策略下,变换器输出电压的波动非常小,约为3.2 V。同时,其动态响应时间仅为18 ms。

附录A图A7给出了负载突增(即负载电阻由15 Ω切换到10 Ω)时,各个模块的输入电压实验波形。从图中可知,在VBC策略下,负载突变时,各个模块的输入电压并没有较大的波动,说明负载突变的暂态过程对于变换器功率均分的影响并不大。但是在VPBC策略下,负载突变几乎不会引起变换器输入电压的波动。

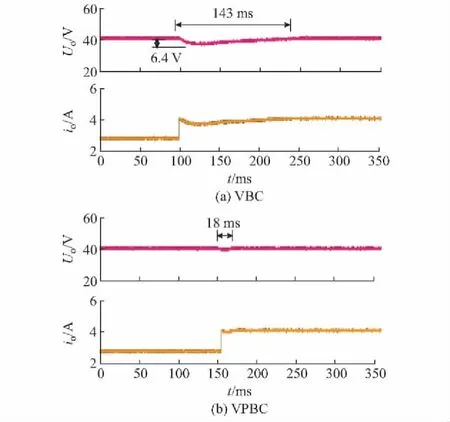
图3 负载突增时不同控制策略的输出电压和负载电流实验波形Fig.3 Experimental waveforms of Uo and iowith different strategies when load steps up

图4给出了输入电压由150 V突减至120 V(即每个DAB模块的输入电压由50 V突减为40 V)时,VBC策略与VPBC策略下的电压实验波形。由图可知,采用VBC策略时,变换器的响应时间为118 ms,输出电压的跌落约为7.5 V;而在VPBC策略下,输出电压的跌落非常小,仅为2.6 V,因此可以认为输出电压基本保持不变。

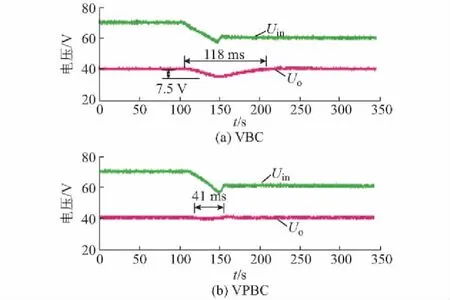
图4 输入电压突减时不同控制策略下的输出电压实验波形Fig.4 Experimental waveforms of Uo with different strategies when input voltage steps down

附录A图A8给出了输入电压突减时(由150 V突减至120 V),分别在VBC与VPBC策略下,每个DAB模块的输入电压波动暂态波形。

由图可知,在变换器电压突变的暂态过程中,VBC策略无法保证各个模块的输入电压(或传输功率)时刻相等,其响应时间约为308 ms;而在VPBC策略下,各个模块的输入电压(或传输功率)时刻保持相等。这表明:相比于VBC,VPBC策略在暂态条件下的控制效果更为明显。

附录A图A9给出了在VPBC策略下,各个DAB模块的电感电流和输出电流。从图中可知,尽管各个模块的辅助电感参数不一致,但在VPBC策略下,各个模块的输出电流平均值近似相等,传输功率基本均分。

4.2 等效IIOP连接DAB实验

对于等效IIOP连接的DAB模块,由于中间直流侧电压已由CHB控制均衡,所以VBC策略不再适用。而VPBC策略不仅仍然适用,而且得到了简化。

图5给出了在VPBC策略下,变换器负载突增(负载电阻由15 Ω切换到10 Ω)和输入电压突减(输入电压由50 V切换到40 V)时的实验波形。从图中可知,无论是负载突变还是输入电压突变,变换器的输出电压均保持稳定,显示了变换器良好的动态特性。

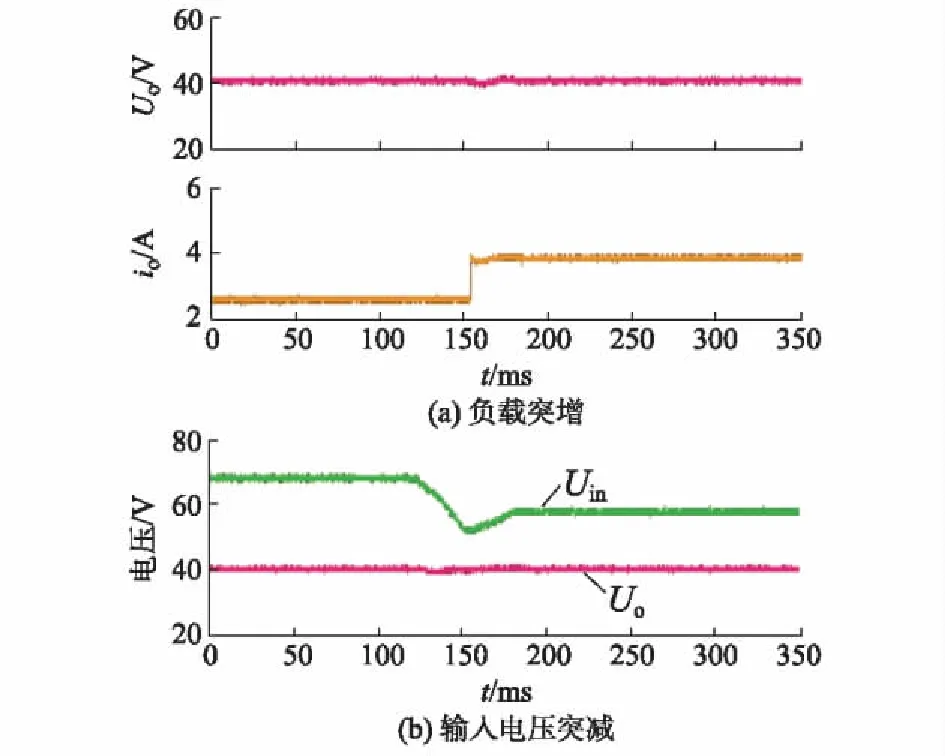
图5 负载突增和输入电压突减时VPBC策略下的电压和电流实验波形Fig.5 Experimental waveforms of Uin, Uo and iowith VPBC strategy when load steps up and input voltage steps down

当各个DAB模块的输入电压为50 V,参考输出电压设定为40 V时,在VPBC策略下,输出并联的DAB变换器由满载(R=5 Ω)切换至空载再切回时的电压电流波形如附录A图A10所示。由图可知,当变换器处于空载状态时,其输出电压略高于参考电压,约为47.7 V。主要原因为:当变换器切换至空载时,即放电回路被切断的暂态过程中,负载侧电容电压升高,控制系统将减小相移量以降低输出电压,然而由于切断负载是在一瞬间完成的,而控制器的调节过程需要一定的时间,所以在负载切断后的一小段时间里,变换器仍在给输出侧电容充电,导致最终的输出电压略大于参考电压。

5 结语

本文针对电力电子变压器中的输出并联DAB式DC-DC变换器,分析了在PET控制过程中,CHB控制策略对于DAB的影响。同时,提出了一种适用于等效ISOP和等效IIOP连接的DAB式DC-DC变换器的VPBC方法。最后,搭建了基于TMS320F28335+FPGA_6SLX45为控制器的三模块输出并联DAB的实验平台,对VPBC方法进行了实验验证,理论分析和实验结果表明该策略具有如下特征。

1)可以有效地解决由于主电路参数不一致造成的传输功率不均衡问题,实现各个模块的传输功率均分。

2)可以显著提高变换器的动态特性,对于负载突变和输入电压突变,变换器的输出电压基本保持稳定。

3)可以显著减小由于负载突变或者输入电压突变造成的变换器瞬时功率传输不均衡程度,使之总是控制在安全运行范围内,降低变换器切换失败率。

4)可以适用于等效ISOP和等效IIOP连接的DAB,即无论前级的CHB使用何种控制方法,该方法都可以实现功率均分,增强了PET控制策略的灵活性。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参考文献

[1] 赵成勇,李路遥,翟晓萌,等.新型模块化高压大功率DC-DC变换器[J].电力系统自动化,2014,38(4):72-78.DOI:10.7500/AEPS20130530014.

ZHAO Chengyong, LI Luyao, ZHAI Xiaomeng, et al. A new type of modular high-voltage high-power DC-DC converter[J]. Automation of Electric Power Systems, 2014, 38(4): 72-78. DOI: 10.7500/AEPS20130530014.

[2] WALKER G R, SERNIA P C. Cascaded DC-DC converter connection of photovoltaic modules[J]. IEEE Transactions on Power Electronics, 2004, 19(4): 1130-1139.

[3] 刘海波,毛承雄.电子电力变压器与常规电力变压器的并联技术[J].电力系统自动化,2008,32(18):49-51.

LIU Haibo, MAO Chengxiong. Parallel technology of electronic power transformer and conventional power transformer[J]. Automation of Electric Power Systems, 2008, 32(18): 49-51.

[4] 侯聂,宋文胜,武明义.全桥隔离DC/DC变换器的直接功率控制方法[J].电力系统自动化,2016,40(17):204-209.DOI:10.7500/AEPS20150816001.

HOU Nie, SONG Wensheng, WU Mingyi. Direct power control scheme of full-bridge isolated DC/DC converters[J]. Automation of Electric Power Systems, 2016, 40(17): 204-209. DOI: 10.7500/AEPS20150816001.

[5] 赵彪,于庆广,孙伟欣.双重移相控制的双向全桥DC-DC变换器及其功率回流特性分析[J].中国电机工程学报,2012,32(12):43-50.

ZHAO Biao, YU Qingguang, SUN Weixin. Bi-directional full-bridge DC-DC converters with dual-phase-shifting control and its backflow power characteristic analysis[J]. Proceedings of the CSEE, 2012, 32(12): 43-50.

[6] OGGIER G, ORDONEZ M, GALVEZ M, et al. Fast transient boundary control and steady-state operation of the dual active bridge converter using the natural switching surface[J]. IEEE Transactions on Power Electronics, 2014, 29(2): 946-957.

[7] DE DONCKER R W A A, DIVAN D M, KHERALUWALA M H. A three-phase soft-switched high-power-density DC/DC converter for high-power applications[J]. IEEE Transactions on Industry Applications, 1991, 27(1): 63-73.

[8] MI C, BAI H, WANG C, et al. Operation, design and control of dual H-bridge-based isolated bidirectional DC-DC converter[J]. IET Power Electronics, 2008, 1(4): 507-517.

[9] ZHAO B, YU Q G, SUN W X. Extended-phase-shift control of isolated bidirectional DC-DC converter for power distribution in microgrid[J]. IEEE Transactions on Power Electronics, 2012, 27(11): 4667-4680.

[10] ZHAO B, SONG Q, LIU W H. Power characterization of isolated bidirectional dual-active-bridge DC-DC converter with dual-phase-shift control[J]. IEEE Transactions on Power Electronics, 2012, 27(9): 4172-4176.

[11] SHI J J, GOU W, YUAN H, et al. Research on voltage and power balance control for cascaded modular solid-state transformer[J]. IEEE Transactions on Power Electronics, 2011, 26(4): 1154-1166.

[12] LI H Z, WANG Y B, YU C H. Research on voltage balance and power balance control for three-phase cascaded multilevel converter based power electronic transformer[C]// 42nd Annual Conference of the IEEE Industrial Electronics Society (IECON 2016), October 24-27, 2016, Florence, Italy.

[13] ZUMEL P, ORTEGA L, LAZARO A, et al. Modular dual-active bridge converter architecture[J]. IEEE Transactions on Industry Applications, 2016, 52(3): 2444-2455.

[14] ZHAO B, SONG Q, LIU W H, et al. Overview of dual-active-bridge isolated bidirectional DC-DC converter for high-frequency-link power-conversion system[J]. IEEE Transactions on Power Electronics, 2014, 29(8): 4091-4106.

[15] ZHAO T F, WANG G Y, BHATTACHARYA S, et al. Voltage and power balance control for a cascaded H-bridge converter-based solid-state transformer[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1523-1532.

[16] SHE X, HUANG A Q, NI X J. Current sensorless power balance strategy for DC/DC converters in a cascaded multilevel converter based solid state transformer[J]. IEEE Transactions on Power Electronics, 2014, 29(1): 17-22.

[17] LIU J Q, YANG J X, ZHANG J P, et al. Voltage balance control based on dual active bridge DC/DC converters in a power electronic traction transformer[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 1696-1714.

[18] 侯聂,宋文胜,武明义.双向全桥DC-DC变换器的负载电流前馈控制方法[J].中国电机工程学报,2016,36(9):2478-2485.

HOU Nie, SONG Wensheng, WU Mingyi. A load current feedforward control scheme of dual active bridge DC-DC converters[J]. Proceedings of the CSEE, 2016, 36(9): 2478-2485.

[19] SEGARAN D, HOLMES D G, MCGRATH B P. Enhanced load step response for a bidirectional DC-DC converter[J]. IEEE Transactions on Power Electronics, 2013, 28(1): 371-379.

[20] BAI H, MI C, WANG C W, et al. The dynamic model and hybrid phase-shift control of a dual-active-bridge converter[C]// 2008 34th Annual Conference of IEEE Industrial Electronics, November 10-13, 2008, Orlando, USA: 2840-2845.

[21] SONG W S, HOU N, WU M Y. Virtual direct power control scheme of dual active bridge DC-DC converters for fast dynamic response[J/OL]. IEEE Transactions on Power Electronics[2007-03-30]. DOI: 10.1109/TPEL.2017.2682982.

[22] 王久和,李华德,王立明.电压型PWM整流器直接功率控制系统[J].中国电机工程学报,2006,26(18):54-60.

WANG Jiuhe, LI Huade, WANG Liming. Direct power control system of three phase boost type PWM rectifiers[J]. Proceedings of the CSEE, 2006, 26(18): 54-60.

[23] SONG Z F, CHEN W, XIANG C L. Predictive direct power control for three-phase grid-connected converters without sector information and voltage vector selection[J]. IEEE Transactions on Power Electronics, 2014, 29(10): 5518-5531.