基于随机矩阵理论的电网状态分析与扰动定位方法

张 力, 张子仲, 顾建炜

(1. 南瑞集团(国网电力科学研究院)有限公司, 江苏省南京市 211106; 2. 国网浙江省电力有限公司, 浙江省杭州市 310009)

0 引言

随着电力技术的不断发展,诸如可再生能源、柔性输电、分布式发电、电动汽车等新技术的注入,电网规模在不断扩大,其复杂程度也日趋增加,电网状态呈现出随机波动、相互耦合的特性。而对电网状态的分析在电力系统技术发展中就不曾停止过,面对日益复杂的电网设备与难度不断增大的电网状态分析现状,研究新的分析方法,克服既有难题与新的困难则显得十分重要。

伴随电网规模的扩大和复杂程度的增加,相应的在线检测与测量技术也在不断发展。广域测量系统(wide area measurement system,WAMS)的投入使用,使得与电网状态相关的数据被更多、更精确地获得,这既是智能电网实现的标志,也是电网状态分析进行更深入研究的基础。随着相量测量单元(phasor measurement unit,PMU)等装置的使用,电网数据以指数级速度在增长[1],这既带来了海量的相关数据,同时也引发了维数灾难等问题[2]。

传统的电网状态分析采用模型法,通过假设和简化来确定具体的数学模型,需要在分析之前完成所有的模型建立和参数确定,不但计算量大,而且结果的准确性也完全依赖于模型的正确性。然而经过假设和简化的模型本身不可避免会带来误差,同时对于不同场景和状况的应用,还需要重新建立相应的模型,难以应对电网不断扩大化和复杂化的现状,也难以达到实时分析的要求。

电网的状态估计方法近年来也不断有新的发展,然而大都是基于模型法。文献[3]分析了已有状态估计方法的特点和存在的主要问题,引入了集合论估计提升估计结果的可信性。文献[4]给出了电网状态脆弱性和结构脆弱性的定义和新评估模型,可基于不同运行状态变量进行电网脆弱性评估。文献[5]提出了适用于地区电网的基于快速解耦的状态估计算法,可以缓解状态估计中计算效率低下的问题。文献[6]由电网线损理论值和实际值之间的差别出发,基于直接神经动态规划的模型进行电网状态估计,可以计算出接近电网实际的线损数据。文献[7]提出了基于改进并行遗传算法的电网状态估计方法,提高了电网状态估计的准确性和速度。

随机矩阵理论(random matrix theory,RMT)是基于大维统计分析的原理建立的。经典极限理论是在假定维数固定,而样本容量趋于无穷的情况下推导出来的。很多经典多元统计法应用于维数很大的数据时,这些方法或者根本无法应用,或者即使应用了,其效率也很低。当维数不是非常大时,早期提出了各种降维方法,如变量选择法、主成分分析法、因子分析法等。但这些方法还是不能适用于维数非常大的情况。所谓大维,在数学上就是指维数与样本容量的比值趋于一个正值常数。对于实际问题,这是不容易判断的,因为维数和样本容量都是给定的值,无法知道比值如何发展。所以研究“大维架构”,就是理论上假定维数和样本容量的比值趋于一个正数,实际应用中则取维数与样本容量的比值。实际经验显示,只要维数不小于10,则应使用大维架构下的极限理论[8]。

以数据为驱动的随机矩阵理论方法不依赖于具体的机理建模,充分利用了历史和实时数据以应对数据量不断增长而导致的数据价值密度低的问题,同时该方法具有普适性,通过高维的统计指标展现复杂电力系统的特性。随机矩阵理论并非新兴的理论,早已在量子理论[9]、金融[10]、无线电[11-12]等领域发挥重要作用。文献[13]首先将随机矩阵的理论应用到了电力系统中,并提出了具体的高维统计指标和数据处理框架。文献[14]沿用文献[13]的数据处理方法分析了配电网运行状态的相关性,提出了有助于不同数据融合的增广矩阵法,将状态量和影响因素相结合。文献[15]采用了增广矩阵法进行了电网静态稳定的态势评估。文献[16]结合了时间序列法和随机矩阵法,同时定义评价指标(evaluation index,EI)进行了电力系统暂态稳定性分析。文献[17]以PMU数据为支撑,描述了随机矩阵理论应用于异常数据检测的方法。文献[18]以在线检测数据为支撑,进行了输变电设备关键性能的评估。文献[19]在电力系统大背景下分析了随机矩阵理论在认知电力系统中的应用思路。

本文基于随机矩阵的理论进行了电网状态分析,以高维统计指标进行状态表征,在此基础上提出了一种电网扰动定位法,该方法阐明了随机矩阵原理应用于区域定位的具体步骤,包括具体的分割依据和定位评判标准。引入了大维统计分析的内容,而结合大维统计分析的知识能够更好地解释随机矩阵原理的作用并提供理论支撑。然后,梳理了具体数据处理的流程,结合大维统计分析中线性谱统计量(linear spectral statistics,LSS)[20]的概念解释了高维统计指标的意义并计算了具体指标的理论期望值。同时,结合已有的知识体系分析了随机矩阵理论的应用基础和数据来源,给出了电网状态分析和扰动定位方法的具体思路。

1 大维统计分析和随机矩阵原理

1.1 大维统计分析

传统的多元统计分析主要以经典的中心极限定理(central limit theorem,CLT)为支柱,经典的中心极限定理的前提则是假定维数不是很大,同时样本量远大于维数。而随着现代技术的不断发展,越来越多的情况下这种假定并不能得到满足,此时经典的极限理论将很难描述现象,甚至完全无效[21]。附录A式(A1)至式(A3)列举了经典的极限理论在大维情况下失效的一个例子。

为了解决经典统计分析的问题,降维的方法被提出,然而随着维数的增长,在保留主要影响因素后仍无法达到经典统计方法的要求。随机矩阵理论的发展则为解决大维数据分析的困难开辟了更广阔的空间。

1.2 随机矩阵原理

顾名思义,随机矩阵就是由随机变量组成的矩阵。随机矩阵的理论起自20世纪四五十年代的量子力学,数学物理学家Wigner突破性地证明了著名的半圆律(semicircle law)[22]。

附录A式(A4)和式(A5)给出了方阵A的经验谱分布(empirical spectrum distribution,ESD)函数的定义。如果有一列方阵An的ESD收敛于极限分布F,则称F为该序列的极限谱分布(limiting spectral distribution,LSD)。

随机矩阵理论中著名的极限谱分布除了半圆律还有M-P律(Marchenko-Patur law)[20],具体内容见附录A式(A6)。而本文所用方法主要依据为单环定理(single ring theorem)[23]和LSS。

1.2.1单环定理

(1)

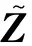
1.2.2LSS

对于随机矩阵X∈CN×N,其LSS定义为:

(2)

式中:λi(i=1,2,…,N)为X的特征根;φ:R→C为测试函数。

由大数定律可知:

(3)

式中:ρ(λ)为特征根λ的PDF。

本文所用的高维统计指标平均谱半径(mean spectral radius,MSR)则属于LSS的一种。

2 状态分析方法

2.1 MSR

由式(2)可知,不同的测试函数对应不同的LSS,LSS本身表征了谱分布的特性,而测试函数起到的作用在某些方面就像是滤波器,应对不同的情况和数据时有着不同的效果[24]。文献[24]中测试了多种测试函数,由结果可知这几种常用的测试函数中MSR的效果最好。

MSR定义如下:

(4)

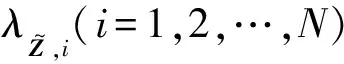
由式(3)可得,当N→∞时,ΦMSR的理论期望值为:

E(ΦMSR)=E(r)=∬r2P(r)drdθ=

(5)

其中,P(r)由式(1)所得。

2.2 状态数据处理

首先需要说明,虽然随机矩阵理论中各种定律的渐近收敛都是在矩阵维数趋于无穷的假设下得到的,但是在工程应用中,在维数适中的情况下,也能得到相当精确的结果[23]。

(6)

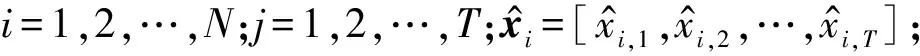
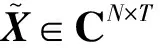
(7)

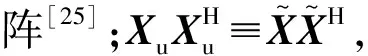
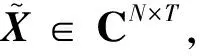
(8)

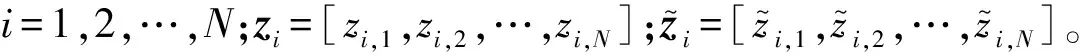
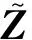
3 随机矩阵理论的应用

3.1 随机矩阵的应用基础

式(9)是电力系统潮流计算的经典方程。由该式可知,对于平衡的稳定电力系统,各节点的电压也是稳定的,量测数据中包含测量误差和小扰动等高斯白噪声。此时由量测数据组成的随机矩阵可以通过随机矩阵原理进行验证,例如本文中采用的单环定理,或者M-P律等其他随机矩阵定理。此时验证的结果符合定理的假设。

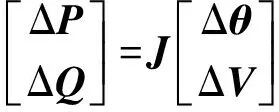
(9)

当网络中出现负荷突变、线路故障或者拓扑改变等情况时,量测数据也将发生突变,此时由历史与实时量测数据构成的矩阵将不再符合随机矩阵原理,因为矩阵已经不再“随机”,通过定理的验证可以判断电网中的事件发生。再通过计算矩阵的相关指标,例如本文中采用的LSS指标,来体现电网状态的具体改变,同时可以根据历史计算指标形成统一的指标规范,从而得以对电网状态进行认知。

3.2 随机矩阵的数据来源

理论上能够组成矩阵的量测数据都可以成为随机矩阵的数据来源,而针对不同的应用场景,可以得到更切实的数据。针对仿真,可以分为稳态仿真,数据来源如Matpower等软件;暂态仿真,数据来源如PSCAD和PSASP等软件。针对实测,数据来源可以为数据采集与监控(SCADA)软件、能量管理系统(EMS)软件、PMU装置等。

例如,基于PMU的WAMS的覆盖使得更多的电网数据可以实时测量,在数据越来越快速和准确地被获得的同时,如何依据大数据建模则成了关键。通过传统的模型法进行分析,并不能及时并充分地利用历史和实时数据,而且模型法随着网络拓扑的改变也要再次建立。

PMU装置以全球定位系统(GPS)为采样基准,进行同步相量的监测,为数据驱动的方式提供了数据基础,为随机矩阵理论的应用提供了原始的样本。

所有的数据来源经过筛选之后,依据时空特性可以按照式(10)所示矩阵的数据结构进行排列,其中N为状态节点数,T为采样节点数。

(10)

3.3 随机矩阵应用于电网状态分析

对于具体的电网,可以选择不同节点的状态量作为数据向量。对于n个节点,每个节点的k个状态量、每个采样时刻ti都可以形成数据向量:

(11)

将数据向量按采样时刻循序排列就得到了原始数据源矩阵:

(12)

为了充分利用历史与实时数据,在时刻ti时选取式(13)所示矩阵进行随机矩阵理论分析。

(13)

依采样时刻进行计算就能得到按时间序列的分析结果以及高维统计指标。具体流程见图1。本文为了简化,于式(1)选择L=1。

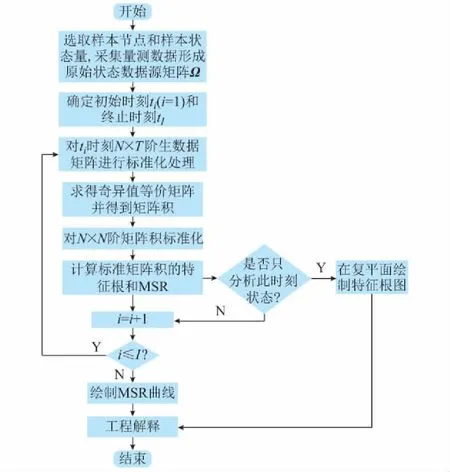
图1 分析方法流程图Fig.1 Flow chart of the analysis method

应用随机矩阵原理的方法同传统的模型法并不相悖,而且还可以相互印证、相互补充,共同进行系统的认知。该分析方法除了可以应用于电网状态分析,还可以采集系统设备状态数据进行状态检修的分析,以及客户终端的用电分析。

3.4 随机矩阵应用于电网扰动定位

本文在采用单环定理验证,确定电网事件发生后,依据节点拓扑,通过合理的矩阵分块分别计算相应的MSR指标,并在图形中进行对比的方式进行电网扰动节点的定位。具体步骤参见算例3。

文献[14]中,作者采用拼接矩阵的方法进行扰动节点相关性的分析,通过计算增广矩阵与参照矩阵相关指标积分面积之差来对比不同节点的相关性,依次进行扰动节点的定位。文献[15]参照文献[14]的增广矩阵法,直接对比不同节点矩阵的相关指标来进行扰动节点的定位。上述两种电网扰动的定位方法都是结合了电压和负荷数据,通过将两种数据进行拼接的方式来组成增广矩阵。本文的方法单纯依靠电压数据,无需各节点的负荷数据。这种方案的好处在于可以减少原始数据的种类,而数据种类的减少意味着采集成本的降低,同时该方案还有迭代更快速的特点,无须对比每个节点的相关性。

4 算例分析

采用IEEE 57节点网络作为算例,以Matpower 6.0作为仿真工具,具体拓扑图如附录A图A1所示。

由式(1)的条件可知,随机矩阵理论对矩阵的维容比是有要求的。这就意味着在状态量确定的情况下,采样点要足够多才能保证定理的有效,所以在固定的测量时间内,采样的时间间隔要满足维容比的要求。而对于受到采样装置条件所限的情况,有两种方法可以保证定理的有效:①延长整体测量的时间,以保证有足够多的采样点;②在原有采样时间间隔和整体测量时间不变的前提下,人为地在采样时间间隔内加入足够多的与前一个采样值相同的采样点,这样处理的后果就是对系统状态变化的评估精度不足,但好处是不需要引入新的采样装置就能采用随机矩阵理论进行状态分析。

表1为事件设置,负荷的突变造成了区域影响。选取每个节点的电压大小作为状态量,N=57,为满足维容比c=N/T∈(0,1],选T=200。通过电压大小状态量来验证突变的发生。

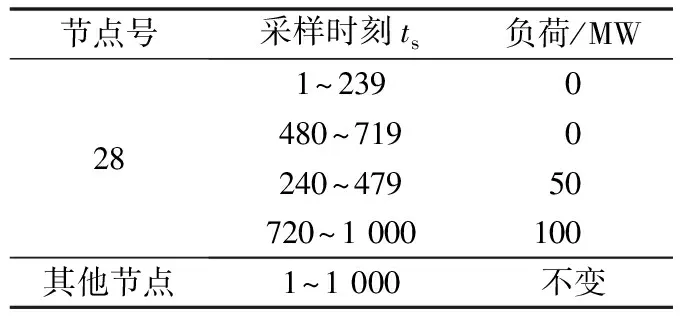
表1 算例1至3中各节点有功负荷的变化情况Table 1 Changes of active loads of buses in cases 1 to 3

其他节点负荷数据见附录A表A1。

4.1 算例1

算例1选取采样时刻ts=40～239和ts=41～240的数据来验证随机矩阵理论的效果。用单环定理分别分析ts=239和ts=240两个采样时刻节点网络的状态。

如图2(a)所示,在时刻ts=40～239,整个节点网络负荷没有波动,状态数据即节点电压大小只有微小的测量误差和波动,此时状态量符合单环定理,状态矩阵的特征根都依式(1)分布在圆环内。

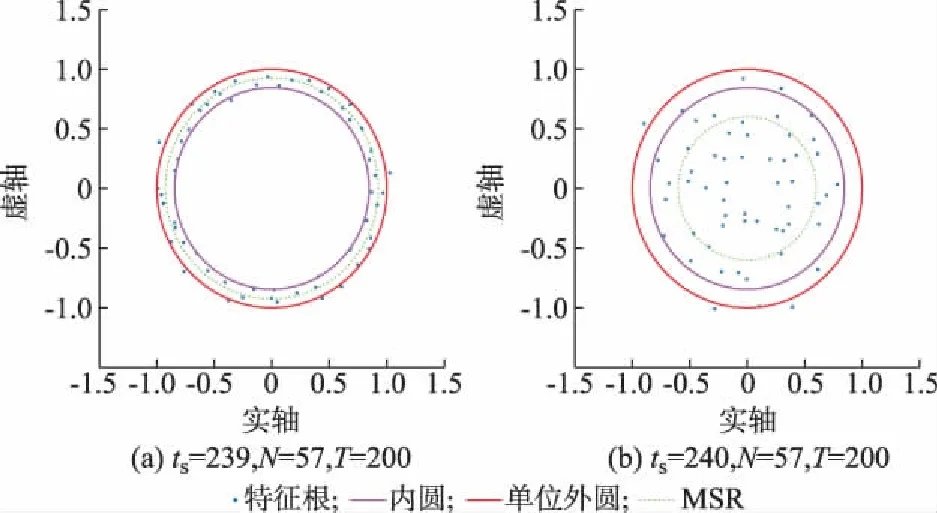
图2 不同状态的单环Fig.2 Single rings of different states

在采样时刻ts=240,如表1所示,节点28的负荷由0上升到50 MW。此时状态数据不再只有高斯白噪声,负荷突变的事件影响了状态数据间的相关性,从而使得状态数据不再符合单环定理。如图2(b)所示,状态矩阵的特征根不再依式(1)分布在圆环内,而是向中心点坍塌。

4.2 算例2

算例2对整个节点网络全采样时刻进行分析,通过计算高维统计指标MSR来分析其状态。由算例1可知,当受事件影响时,状态矩阵的特征根将会发生坍塌,而根据式(4)可知MSR在此时也会发生突变。

如图3所示,由于T=200,MSR的计算从ts=200开始。ts=239时,MSR在0.9附近,而ts=240时则突变到0.6附近,说明在ts=240时,节点网络受事件影响,与算例1结果相同。

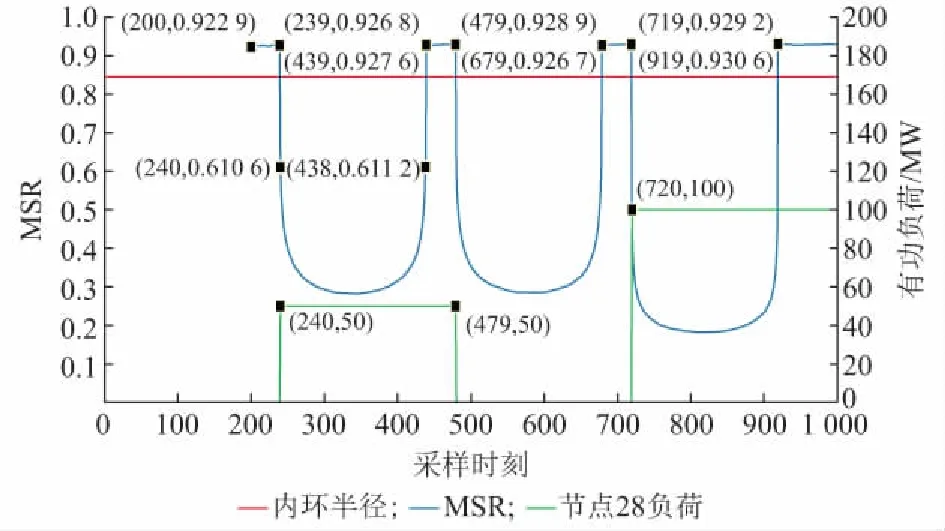
图3 全网络基于时间序列的MSR(N=57,T=200)Fig.3 Time series based MSRs of the whole network (N=57,T=200)

ts=439时,采样时刻ts=240～439中的状态数据都是在新的状态下达到平衡,所以此时MSR恢复到初始水平。需要注意的是,MSR恢复了稳定,并不说明系统在一个采样周期内波动就结束了。本文的方法是采用数据驱动,不涉及具体的机理过程,所以算例并不涉及电网的暂态过程。

图3中,在不同的状态下达到平衡后MSR都会恢复到0.9附近,而与不同的状态无关,由式(5)可知,这是因为E(ΦMSR)只与维容比有关。

分析ts=240和ts=480以及ts=720时MSR的突变可知,负荷变化越大则MSR突变程度越大。

4.3 算例3

在工程实际中,传统的方法对于数据的利用还停留在低维的认识上,如SCADA电压大小的越限告警,只能在经验基础上设置越限值,准确性和灵敏度本身存在矛盾,也完全依赖经验值,同时很难通过电压大小的波动来确定具体的扰动区域,如附录A图A2所示(纵坐标表示电压大小的标幺值)。

由于扰动的影响是对整个区域作用的,传统的方法中很难通过越限监测来实现具体扰动的定位,而通过本文提出的方法则不但能够实现,而且是很直观的定位扰动区域。

由算例2可知,MSR的突变程度反映了节点网络受影响的程度。同时,分析的对象是状态矩阵,而矩阵形式的优势之一就是便于分割。结合这两点,本文提出了电网扰动定位的方法。以节点拓扑图为依据,将整个节点网络按照拓扑关系进行分割。

如附录A图A1所示,先将整个节点网络分割成Part 1和Part 2两部分。分割的要求就是按照拓扑连接关系,将相互连接最近的节点划归为同一区域,且保证分割后的矩阵维数相近。图中,将节点22至43和52至57共28个节点划为Part 1,将节点1至21和44至51共29个节点划为Part 2。然后对两个区域分别进行MSR的计算,由图4可得,Part 1区域的突变明显大于Part 2。所以将扰动区域定位于Part 1。

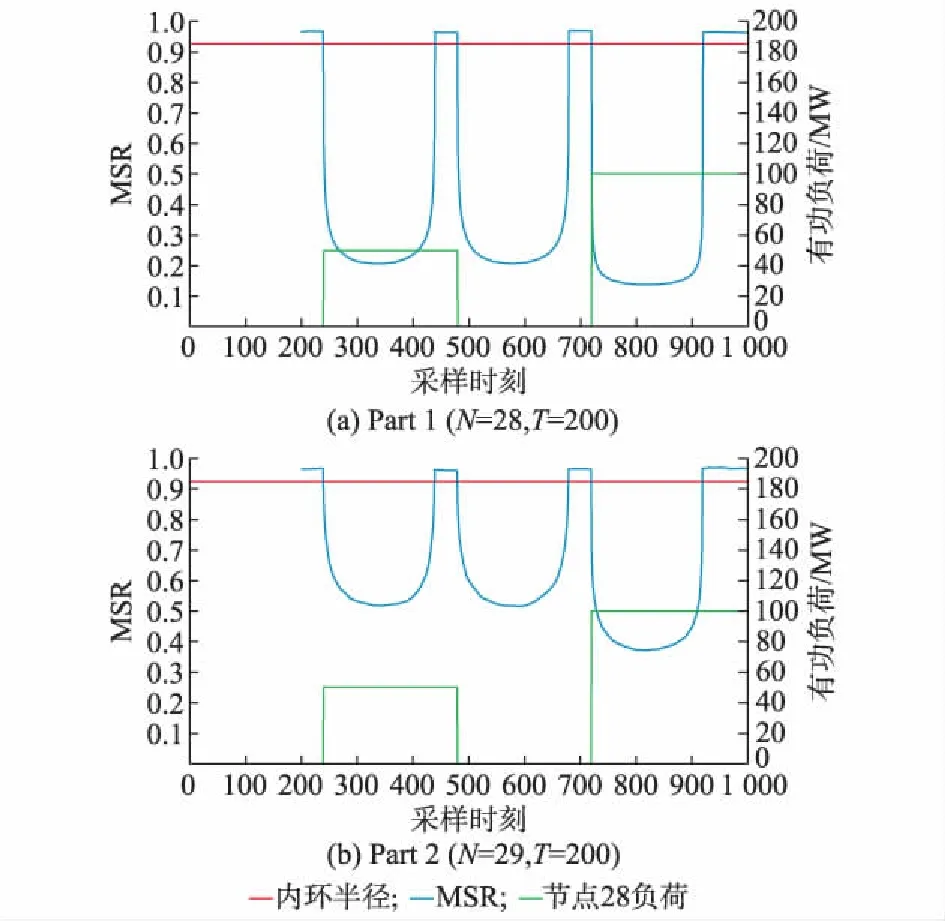
图4 Part 1和Part 2的MSRFig.4 MSRs of Part 1 and Part 2

继续重复上面的步骤,如附录A图A1所示,将Part 1划分为Part 1A和Part 1B两个区域。节点22至31和52至55共14个节点为Part 1A,节点32至43和56至57共14个节点为Part 1B。分别对这2个区域进行MSR计算,由图5可得,Part 1A区域的突变明显大于Part 1B。所以将扰动区域定位于Part 1A。由附录A图A1可知,节点28的确在Part 1A中,符合实际情况。

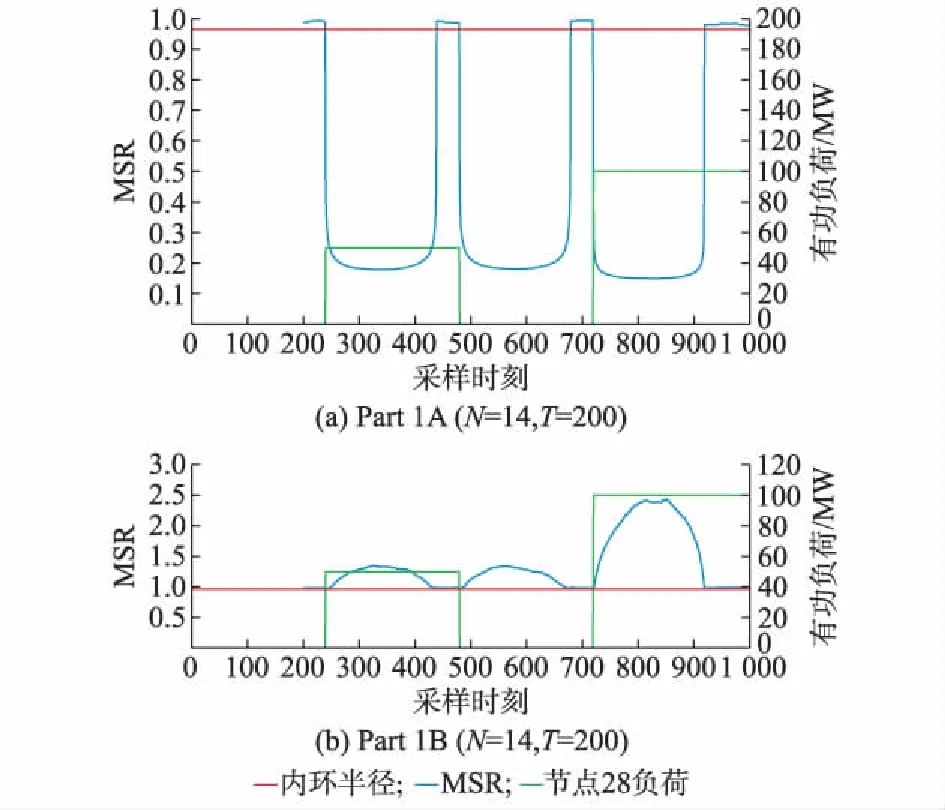
图5 Part 1A和Part 1B的MSRFig.5 MSRs of Part 1A and Part 1B

附录A图A3考虑了扰动节点在分区边界的情况。扰动定位的结果一致,说明本文所提方法对于扰动发生在分区边界时依然有效。而且由图5(b)和附录A图A4左侧可知,发生扰动时,单环定理中特征根可能向圆心坍塌,也可能向单位圆外发散。

受随机矩阵维数大小的限制,这种方法并不能无限分割,然而却依然显著将扰动区域定位,尤其是当系统本身很庞大时,这种分割就可以进行更多的次数,直到定位于十数维的区域,因此所提区域定位法不但不受维数灾难的影响,而且随着系统维数增大,效果更明显。同时,此方法不涉及具体机理模型,可以充分利用历史和实时数据,而且具有良好的响应速度,可以进行实时分析。

5 结语

本文利用随机矩阵原理分析了电网状态,同时提出了电网扰动定位的方法。算例1验证了单环定理在电网状态分析中的效果,其中状态量的选择除了案例中的电压大小,其他电力系统中常用的电压幅角、电流、功率等同样可以采用,该方法适用于电网状态断面分析。算例2验证了高维指标下电网的状态分析,该方法适用于电网状态时间序列分析。算例3提出并验证了电网扰动定位的方法。需要说明的是,本文限于仿真软件的限制只采用了IEEE 57节点的网络进行算例分析,而实际中随机矩阵理论完全可以处理更多节点的系统。

本文的算例是以仿真数据为依据,并没有采用实际数据中可能存在的坏数据和不同步数据。对于坏数据,如果是数据缺失或者是明显偏离实际的数据,则在数据预处理中可以采用中项均值替代的方法处理。而对于不同步数据,采用单环定理验证方法的状态分析结果并不受影响,采用LSS的方法进行高维指标分析时的时间参数会受影响但状态变化分析不受影响,并且可以在明确不同步时间后进行相应修正。这部分将在以后的研究中进一步完善。同时,本文所提方法在大数据的运算量和运算速度上也有待进一步实际验证。

随机矩阵原理不依赖于具体的数学模型,没有确定机理模型过程中的假设和简化,提高了历史和实时数据的利用率。同时从高维指标的角度观察电网状态,经算例验证,具有相当的灵敏度和准确性。然而随机矩阵理论的应用还需要更多的发掘,需要结合更多的实际情况,从而具体解决电力系统中的相关工程问题。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参考文献

[1] 宋亚奇,周国亮,朱永利.智能电网大数据处理技术现状与挑战[J].电网技术,2013,37(4):927-935.

SONG Yaqi, ZHOU Guoliang, ZHU Yongli. Present status and challenges of big data processing in smart grid[J]. Power System Technology, 2013, 37(4): 927-935.

[2] MOULIN L S, DA SILVA A P A, EL-SHARKAWI M A, et al. Support vector machines for transient stability analysis of large-scale power systems[J]. IEEE Transactions on Power Systems, 2004, 19(2): 818-825.

[3] 何光宇,常乃超,董树锋,等.基于集合论估计的电网状态辨识:(一)建模[J].电力系统自动化,2016,40(5):25-31.DOI:10.7500/AEPS20150529012.

HE Guangyu, CHANG Naichao, DONG Shufeng, et al. Power system state identification based on set theory estimation: Part one modelling[J]. Automation of Electric Power Systems, 2016, 40(5): 25-31. DOI: 10.7500/AEPS20150529012.

[4] 魏震波,刘俊勇,朱国俊,等.基于电网状态与结构的综合脆弱评估模型[J].电力系统自动化,2009,33(8):11-14.

WEI Zhenbo, LIU Junyong, ZHU Guojun, et al. A new integrative vulnerability evaluation model to power grid based on running state and structure[J]. Automation of Electric Power Systems, 2009, 33(8): 11-14.

[5] 杨翾,王坚俊,唐剑,等.基于快速解耦算法的地区电网状态估计研究[J].高压电器,2017,53(1):102-107.

YANG Xuan, WANG Jianjun, TANG Jian, et al. Research on regional power grid state estimation based on fast-decoupled algorithm[J]. High Voltage Apparatus, 2017, 53(1): 102-107.

[6] 卢志刚,李爽.基于直接神经动态规划的电网状态估计及理论线损计算[J].电网技术,2008,32(23):50-55.

LU Zhigang, LI Shuang. Power system state estimation and theoretical line loss calculation based on direct neural dynamic programming[J]. Power System Technology, 2008, 32(23): 50-55.

[7] 吴杰,卢志刚,杨斌,等.基于改进并行遗传算法的电网状态估计[J].电网技术,2006,30(18):64-68.

WU Jie, LU Zhigang, YANG Bin, et al. Power network status estimation based on improved parallel genetic algorithm[J]. Power System Technology, 2006, 30(18): 64-68.

[8] 白志东,郑术蓉,姜丹丹.大维统计分析[M].北京:高等教育出版社,2012.

[9] BRODY T A, FLORES J, FRENCH J B, et al. Random-matrix physics: spectrum and strength fluctuations[J]. Reviews of Modern Physics, 1981, 53(3): 385-479.

[10] LALOUX L, CIZEAU P, POTTERS M, et al. Random matrix theory and financial correlations[J]. International Journal of Theoretical and Applied Finance, 2000, 3(3): 391-397.

[11] QIU R C, HU Zhen, CHEN Zhe, et al. Cognitive radio network for the smart grid: experimental system architecture, control algorithms, security, and microgrid testbed[J]. IEEE Transactions on Smart Grid, 2011, 2(4): 724-740.

[12] QIU R C, WICKS M. Cognitive networked sensing and big data[M]. New York, USA: Springer, 2013.

[13] HE Xing, AI Qian, QIU R C, et al. A big data architecture design for smart grids based on random matrix theory[J]. IEEE Transactions on Smart Grid, 2017, 8(2): 674-686.

[14] XU Xinyi, HE Xing, AI Qian, et al. A correlation analysis method for power systems based on random matrix theory[J]. IEEE Transactions on Smart Grid, 2017, 8(4): 1811-1820.

[15] 吴茜,张东霞,刘道伟,等.基于随机矩阵的电网静态稳定态势评估方法[J].中国电机工程学报,2016,36(20):5414-5420.

WU Qian, ZHANG Dongxia, LIU Daowei, et al. A method for power system steady stability situation assessment based on random matrix theory[J]. Proceedings of the CSEE, 2016, 36(20): 5414-5420.

[16] 刘威,张东霞,王迎新,等.基于随机矩阵的电力系统暂态稳定性分析[J].中国电机工程学报,2016,36(18):4854-4863.

LIU Wei, ZHANG Dongxia, WANG Yingxin, et al. Power system transient stability analysis based on random matrix theory[J]. Proceedings of the CSEE, 2016, 36(18): 4854-4863.

[17] 魏大千,王波,刘涤尘,等.高维随机矩阵描述下的量测大数据建模与异常数据检测方法[J].中国电机工程学报,2015,35(增刊1):59-66.

WEI Daqian, WANG Bo, LIU Dichen, et al. A method for wams big data modeling and abnormal data detection with large random matrices[J]. Proceedings of the CSEE, 2015, 35(Supplement 1): 59-66.

[18] 严英杰,盛戈皞,王辉,等.基于高维随机矩阵大数据分析模型的输变电设备关键性能评估方法[J].中国电机工程学报,2016,36(2):435-445.

YAN Yingjie, SHENG Gehao, WANG Hui, et al. The key state assessment method of power transmission equipment using big data analyzing model based on large dimensional random matrix[J]. Proceedings of the CSEE, 2016, 36(2): 435-445.

[19] 贺兴,艾芊,邱才明,等.随机矩阵理论在电力系统认知中的应用初探[J].电网技术,2017,41(4):1165-1173.

HE Xing, AI Qian, QIU Caiming, et al. A primary study on the situation awareness of power systems using random matrix theory[J]. Power System Technology, 2017, 41(4): 1165-1173.

[20] BAI Zhidong, SILVERSTEIN J W. Spectral analysis of large dimensional random matrices[M]. New York, USA: Springer, 2010.

[21] 姜丹丹.大维随机矩阵谱理论在多元统计分析中的应用[D].长春:东北师范大学,2010.

[22] MADAN M L. Random matrices[M]. Amsterdam, Netherlands: Elsevier Academic Press, 2004.

[23] QIU R C, PAUL A. Smart grid using big data analytics: a random matrix theory approach[M]. Hoboken, USA: John Wiley and Sons, 2017.

[24] HE Xing, QIU R C, AI Qian, et al. Designing for situation awareness of future power grids: an indicator system based on linear eigenvalue statistics of large random matrices[J]. IEEE Access, 2016, 4: 3557-3568.

[25] CAKMAK B. Non-hermitian random matrix theory for mimo channels[D]. Trondheim, Norway: Norwegian University of Science and Technology, 2012.