基于概率潮流的主动配电网日前—实时两级优化调度

黄 伟, 葛良军, 华亮亮, 杨舒文, 刘明昌

(1. 华北电力大学电气与电子工程学院, 北京市 102206;2. 国网内蒙古东部电力有限公司通辽供电公司, 内蒙古自治区通辽市 028000)

0 引言

随着环保压力与能源危机的不断加重,电力作为应用最为广泛的二次能源,正在进行源、荷双重技术革命,即分布式电源(DG)、储能系统、柔性负荷等分布式能源(DER)大规模并网运行[1-3]。相对于传统配电网,DER的接入一方面导致潮流双向流动,另一方面其本身往往具有较强的波动性,难以准确预测。因此配电网运行边界条件更加复杂。

传统配电网不能有效对DER实现主动管理,无法满足配电网未来发展需求。为此主动配电网(ADN)应运而生[4]。它通过灵活的拓扑结构、先进的调度策略对DER进行主动管理,实施需求侧响应引导源荷参与互动[5],保障配电网经济安全运行的同时实现DER的高效消纳。

ADN优化调度包含有日前调度和实时调度[6],前者根据日前负荷和DER预测结果制定次日24 h内各单元购、发电计划;后者根据实际运行工况和超短期预测结果,对日前调度做出相应调整优化,时间尺度多以15～30 min为主[7]。

文献[8]运用多代理对DER进行管控,构建日前—实时多时间尺度调度模型,实现ADN运行经济性和稳定性,但未充分考虑ADN中间歇性电源和柔性负荷不确定性;文献[9]在日前调度中运用多场景技术拟合ADN运行中不确定因素,使运行收益期望值达到最优,但其调度过程侧重于功率分配,未充分考虑配电网运行安全性;文献[5]考虑ADN的不确定性,提出基于概率潮流的日前调度模型,但考虑到日前预测较大的波动性,可能会使得概率潮流的计算误差有所增加,影响调度精度;文献[10]通过“源荷双侧”的协同性处理ADN中的随机性,提出运行成本与环境成本最优的供需互动优化调度策略。

现有研究尚未针对实时调度中超短期预测结果的波动性加以考虑,可能会使得调度安全裕度小,系统稳定性差。概率潮流能够有效反映系统中各因素波动对系统运行的影响,适合应用于预测时间尺度短、预测波动小的实时调度[11]。为此本文提出基于概率潮流的日前—实时两级优化调度策略,日前调度根据ADN日前预测结果,确定ADN中各调度单元次日运行计划;然后结合实际运行时工况和超短期预测结果,考虑各不确定因素,基于概率潮流进行实时调度,对日前计划进行修正,降低运行成本并确保各不确定性变量在正常范围内波动时,ADN能够主动有效应对,提高系统安全裕度,实现安全经济运行。

1 ADN调度框架

1.1 调度机制与调度单元

ADN调度框架见附录A图A1,主要组成单元包括DG、虚拟微网(VMG)、负荷、储能系统等。

1)DG

DG分为可控电源和间歇式电源(IPS),前者主要有微型燃气轮机、燃料电池等,其出力大小完全受控,可提前确定发电计划,下面以微型燃气轮机为例进行讨论。后者主要为分布式风电和光伏,其最大出力受风速、光照等因素决定,具有很强的波动性,一般根据天气预报对其未来出力大小进行预测,难以精确控制。

2)VMG

VMG是指不参与ADN统一管理调度的配电区域,经营权往往属于第三方,能够独立控制调度其内部资源[5]。VMG是传统微网概念的延伸,具有专属的调度中心,根据自身内部DER信息、负荷预测以及电价等制定购售电计划,以区域作为整体与ADN进行功率交换,最大化自身收益。具有独立调控中心的微网、虚拟发电厂[12]等都属于此范畴。

从ADN角度看,VMG在不同情况下角色不同,既可能作为电源向电网售电,也可能作为负荷向ADN购电。且其内部DER、负荷的波动也使得VMG与ADN功率交换具有一定不确定性。

3)负荷

负荷包括常规负荷和柔性负荷。前者通常指弹性较小的刚性负荷,一般不参与需求响应;后者一般会主动参与源荷供需互动,根据激励或电价积极调整自身用电计划,能够有助于电网经济稳定运行。柔性负荷既含电动汽车、储能等具有“源荷”双重特征的新型负荷[13],也含有一定用电弹性的传统负荷。

1.2 不确定性分析

间歇式电源、负荷与VMG购售电受多种因素影响,预测结果均存在一定程度的不确定性。概率学上认为正态分布可近似分析目前大部分的概率分布,是最常用的一类分布函数。目前有部分文献应用正态分布对配电网中的不确定因素进行分析[9],各单元分布如表1所示。表中:f1(PPV,t),f2(PWT,t),f3(PVMG,t),f4(PIL,t)分别为超短期预测时段t内光伏、风机、VMG和柔性负荷的功率概率密度函数;PPV,t,PPVP,t,δPV,t分别为时段t内光伏出力预测最大值、期望值和标准差(其他变量同理,不一一叙述)。

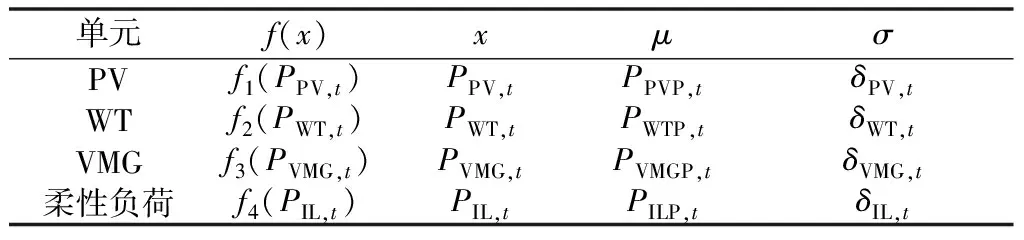
表1 正态分布模型参数Table 1 Model parameters of normal distribution

2 概率潮流

ADN中不确定单元使系统运行状态具有一定的不确定性。本文在实时调度中应用概率潮流,将各不确定单元功率作为随机变量,求出节点电压与支路功率概率分布[14],从而在确保运行时节点电压和支路功率不发生越限的前提下使目标函数最优,实现系统安全经济运行。式(1)为节点电压方程。

(1)

式中:Pi和Qi分别为节点i注入有功功率和无功功率;θij为节点i,j之间电压相角差;Vi和Vj分别为节点i,j的电压幅值;Gij和Bij为节点导纳矩阵对应元素;N为系统节点集。

可将式(1)写成矩阵形式:

S=f(X)

(2)

同理,支路功率方程如式(3)和式(4)所示。

(3)

(4)

式中:Pij和Qij分别为节点i向节点j所传输有功和无功功率;kij为线路i-j上变压器的变比;bij0为线路i-j容纳的一半。

可写成矩阵形式为:

Z=g(X)

(5)

对式(2)和式(5)进行泰勒级数展开,并忽略其中二次项及以上,可得:

(6)

式中:J0为雅可比矩阵;G0=∂Z/∂X|X=X0。

变换式(6)可得:

(7)

根据半不变量可加性[15]的特点,可通过输入功率半不变量求节点电压和支路功率半不变量,继而运用级数得到其概率分布。

3 优化调度模型

3.1 日前调度

3.1.1目标函数

基于负荷、分布式风光出力和VMG购售电日前预测结果,以ADN全周期内运行成本最小为目标函数进行日前调度,确定各时段DG发电功率、与主网和VMG购售电功率以及储能系统充放电功率。将一天24 h分为T个时段,假定每一时段内各组成单元功率基本保持不变,目标函数为:

(8)

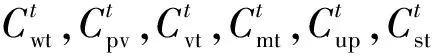
1)分布式风光发电成本

风光发电成本包括建设成本和运行成本,根据其全寿命内发电总量估计,折合到单位发电量里,如式(9)所示。

(9)

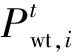
2)VMG购售电成本

(10)

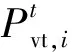
(11)

3)微型燃气轮机发电成本

(12)

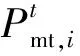
4)主网购售电成本

(13)

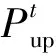
5)储能系统运行成本

储能系统运行成本包括安装费用与维护费用,即

(14)

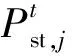
3.1.2不等式约束

1)功率平衡约束

(15)

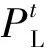
2)储能系统约束

(16)

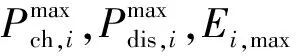
3)各调度单元均需满足的约束

(17)

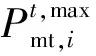
4)节点电压和支路功率约束

(18)

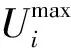
3.2 实时调度

3.2.1目标函数

实时调度充分考虑部分可调度单元的不确定性,结合ADN实际运行工况和超短期预测结果及概率分布进行计算分析,通过控制可中断负荷中断、调整各调度单元运行计划和变压器变比,使ADN在满足安全约束前提下实现调度成本最优。

对于ADN而言,上级主网和VMG是相对独立的利益主体。实时调度中ADN若要改变日前调度中同其确定的交互功率值,则主网和VMG须作出相应调整,会影响其自身收益,因此本文考虑违约惩罚。而ADN所属的DG为其自身资源,可以根据自身利益进行调整。目标函数见式(19)。

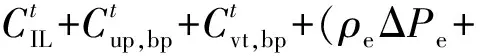
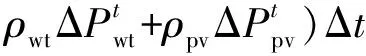
(19)

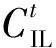
1)中断负荷补偿费用

可中断负荷通常提前和电力公司签订合同,当电网处于紧急状态下,可予以切除,保障电网安全,并按照合同获得经济赔偿。一般按照梯度补偿机制进行补偿[10],如附录A图A2所示,将可中断负荷量划分为K个等级,各等级中断单位负荷赔偿价格为CK,则补偿成本为:

(20)

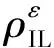
2)违约赔偿费用

当ADN向主网实际购售电量与日前调度确定电量偏差大于阈值时,超过部分收取违约成本,如式(21)所示。

(21)

式中:Pup,limit为主网偏差阈值;ΔPup为向主网实际购电量与计划购电量偏差;ρup,bp为超出阈值向主网单位电量赔偿成本。

同理,VMG违约补偿为:

(22)

式中:Pvt,limit为VMG偏差阈值;ΔPvt为VMG实际购电量与计划购电量偏差;ρvt,bp为超出阈值向VMG单位电量赔偿成本。

3.2.2不等式约束

为保证ADN安全运行,实时调度时需预留足够的安全裕度。为此应用概率潮流计算各不确定性单元引起的节点电压和支路功率概率分布,调度过程中使得节点电压与支路功率在3倍标准差内波动时满足约束条件。

(23)

式中:i，j∈N；δΔUi和δΔSij分别为节点电压与支路功率标准差。

此外,可中断负荷、储能系统和变压器变比满足以下约束:

(24)

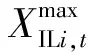
除此之外,实时调度仍需满足约束式(15)至式(17)。

3.3 模型求解

引力搜索算法(GSA)具有搜索能力强、收敛快等优点[16],但它只能基于本代粒子及其适应值进行下一时刻速度和位置跟新,易陷入局部最优。粒子群算法[17]具有记忆迭代过程中全局最优粒子和局部最优粒子的特点,因此可参照粒子群算法改进GSA中粒子记忆性,其速度和位置更新如式(25)所示。

(25)

式中:ai(t),Vi(t),Xi(t)分别为第t代粒子i加速度、速度和位置;pbest,i为粒子i迄今搜索到的最优位置;gbest为整个物质群迄今搜索到的最优位置;r1,r2,r3为0～1间随机数;c1和c2为学习因子。

图1为实时调度求解流程(日前调度求解流程见附录A图A3)。其中粒子是指优化模型的一个可能解,以向量x=[x1,x2, …,xn]表示,n表示解的维数,即所求变量个数。日前调度中解每一维分别为风机、光伏、VMG购售电,微型燃气轮机、主网购电和储能系统充放电功率期望值;实时调度解的每一维分别为各调度单元功率调整量和负荷中断量期望值以及变压器变比。

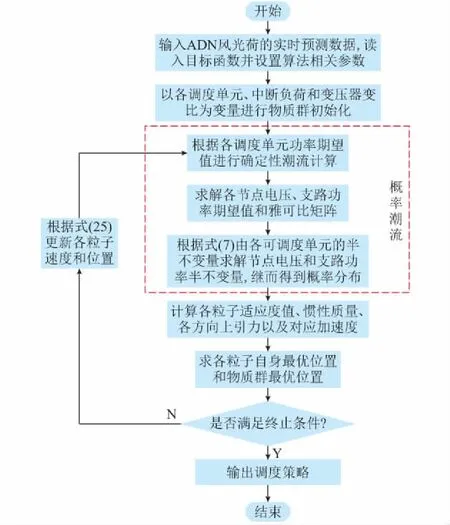
图1 实时调度计算流程Fig.1 Calculation process of real-time scheduling

适应度计算公式为:

(26)

式中:F为目标函数;Hi为第i个约束惩罚项,若约束i满足约束,Hi=0,否则Hi为越限值;λi为约束i的惩罚系数。

4 算例分析

本文利用改进的IEEE 14节点ADN验证调度策略的有效性,图2为其拓扑结构,ADN包含3条馈线,共14个节点,基础参数见附录B表B1。其中节点1通过变压器与主网相连,变压器变比范围为1±4×1.25%。分布式风电、光伏和微型燃气轮机分别通过节点7,9,14接入ADN,VMG通过节点10接入ADN,储能系统通过节点8接入ADN,节点3和节点11接有可中断负荷。负荷、分布式风电与光伏、VMG功率日前预测如附录A图A4和图A5所示。

参考文献[18],主网电价分为峰、谷、平,见附录A图A6,分别为0.55,0.488,0.33元/(kW·h)。设微型燃气轮机发电成本为0.51元/(kW·h),其夜间负荷低谷期处于停机状态,白天08:00—24:00处于运行状态,最大和最小输出功率分别为6 MW和3 MW;储能系统容量为4 MW,充放电功率限值为2 MW。各调度单元发电成本详见附录B表B2。

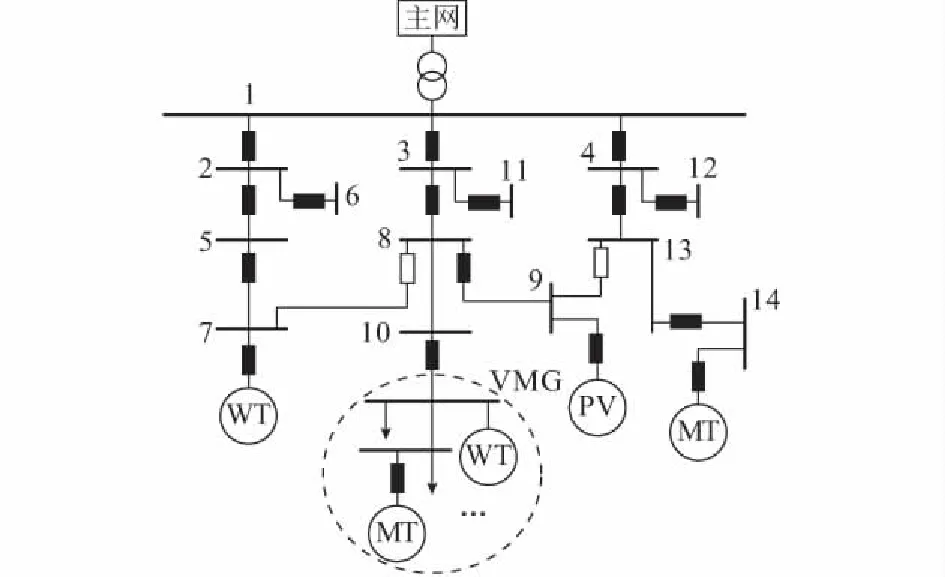
图2 ADN拓扑结构Fig.2 Topological structure of ADN

1)日前调度结果分析

图3为ADN日前调度结果。风光发电成本主要集中在建设投资时,运行成本较低且有政府补贴;VMG购售电价也较低。因此日前调度这三者在满足约束时尽可能以最大功率消纳,调度结果见附录B表B3。在00:00—08:00时段处于负荷低谷,主网电价低至0.33元/(kW·h),此时储能处于充电状态。时段08:00—12:00内,负荷逐渐增加,微型燃气轮机开始运行。此时段微型燃气轮机发电成本略高于主网电价0.488元/(kW·h),因此以最低功率运行,储能系统既不充电也不放电。在12:00—15:00时段和17:00—22:00时段内,负荷处于高峰期,主网的电价高达0.55元/(kW·h),此时微型燃气轮机满载运行,储能系统以较大的放电功率向电网供电。15:00—17:00时段内主网电价为0.488元/(kW·h),此时段微型燃气轮机低功率运行,而储能系统为应对即将到来的负荷高峰快速充电。

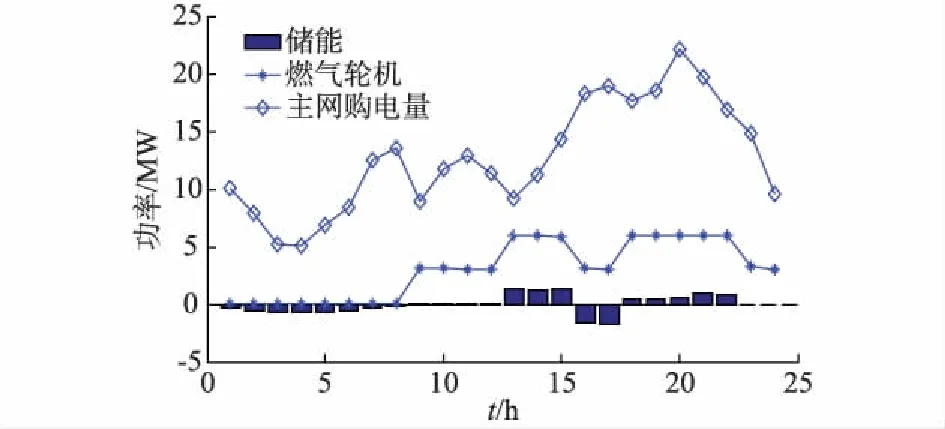
图3 日前调度各时段各单元功率值Fig.3 Power value of each unit dispatched by day-ahead scheduling

2)实时调度结果分析

以14:00—15:00时段为例进行实时调度。日前调度确定此时段同主网和VMG签约功率分别为14.31 MW和0.93 MW,前者实际购电功率与日前调度结果偏差不得超过1 MW,后者为实际功率与日前调度结果偏差不得超过0.5 MW。超过部分需支付违约赔偿,价格均为600元/(MW·h)。节点3和11负荷可中断量分别为1.5 MW和1 MW,中断赔偿价格见附录B表B4。超短期预测这一时段各节点负荷期望值、DER功率以及VMG最大交互功率见附录B表B5和表B6。对此时段设计3种场景进行分析。

场景1:风光功率波动分别为±10%与±8%,VMG功率波动±6%,节点3和11处负荷波动为±6%。

场景2:风光功率波动分别为±6%与±4%,VMG功率波动4%，节点3和11负荷波动±4%。

场景3:风光功率波动分别为±4%与2%,VMG功率波动±2%,节点3和11负荷波动±2%。

实时调度求得各调度单元功率期望值如表2所示。图4为三种场景下节点9和10的电压概率分布。

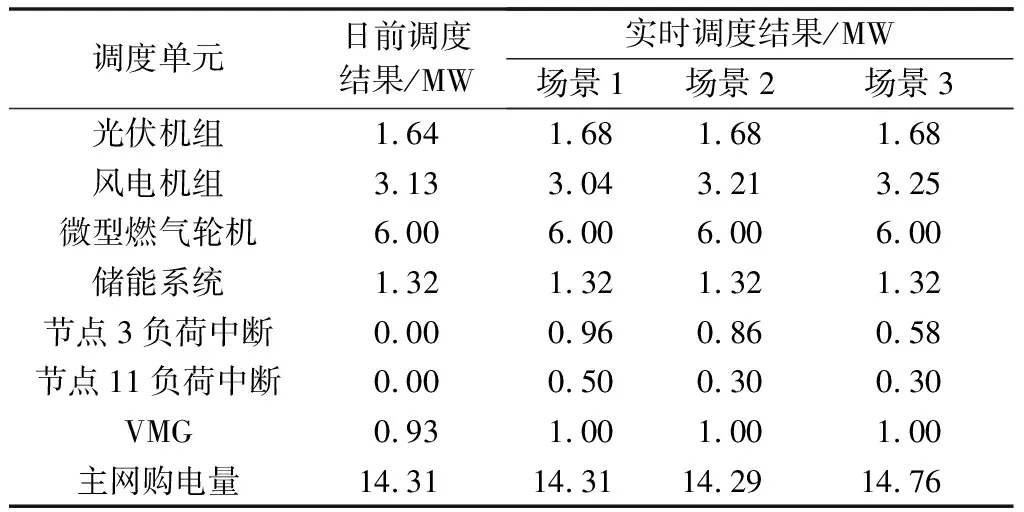
表2 某一时段不同场景可调度单元运行计划Table 2 Operation plans of scheduling units under different cases in a certain period

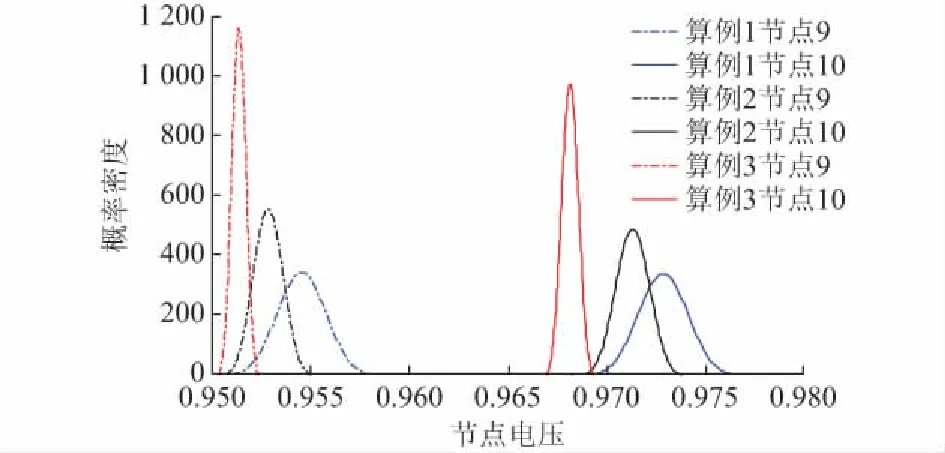
图4 不同场景下部分布节点电压概率密度分布Fig.4 Voltage probability density distribution of partial nodes under different cases

由附录B表B5可知:此时段馈线1负荷较轻而馈线2负荷很重。结合图4和表2可知,节点电压在场景1中波动性最大,须预留最多的安全裕度,防止越限,为此场景1中负荷中断量和弃风量均最大,同理场景2次之。3种场景下储能系统和VMG功率均已达到约束条件下的最大值,主网和VMG购售电量偏差均小于规定值,无需违约惩罚。各场景下节点电压波动范围见附录B表B7。

表3对比了3种调度模式下调度结果,调度模式分别为:①本文所提的基于概率潮流的实时调度;②不进行实时调度,遵守日前调度计划,功率差额由上级主网进行调节;③未考虑不确定单元功率波动,基于确定性潮流的实时调度。

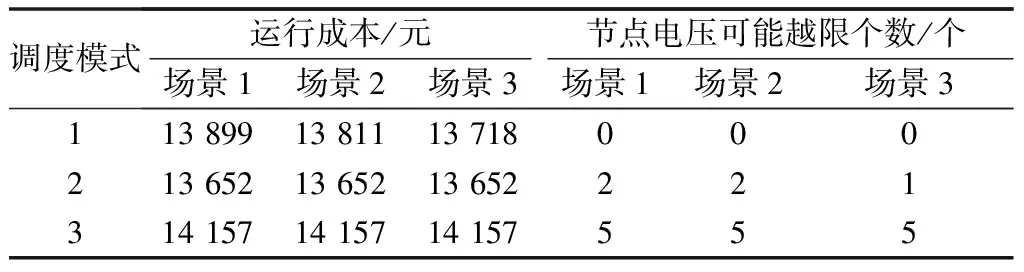
表3 某一时段不同调度方式运行结果对比Table 3 Comparison of operation results under different scheduling models in a certain period

调度模式2和3均未考虑不确定性单元波动性,因此在3个场景下调度方案和运行成本期望值均相同,但不同场景下节点电压越限个数可能不同,如调度模式2的场景2和3。由表3可知,调度模式3未进行实时调度,运行成本最高,且5个节点有可能发生电压越限,存在较大运行风险。调度模式1在3个场景下运行成本较调度模式3分别下降了1.86%,2.51%和3.20%,且节点电压不发生越限。因此调度模式1兼顾了系统运行的经济性和安全性,且随着不确定性单元波动性减小,运行成本能够稍有下降。调度模式2成本最低,但未考虑不确定性单元波动性,使得节点电压的安全裕度较低,可能会发生节点电压越限。ADN线路有足够的容量裕度,3种调度模式中均未发生支路功率越限。

5 结语

本文充分考虑ADN不确定单元功率波动性,提出了基于概率潮流的日前—实时两级优化调度策略。日前调度基于日前预测结果,确定次日ADN各时段向主网购售电电功率、与VMG交换功率大小以及DG、储能的运行计划;实时调度结合ADN实时运行工况和超短期预测结果,应用概率潮流计算计及不确定单元的波动性,优化调整日前调度安排和制定负荷中断计划。该调度模型兼顾了系统运行的经济性和安全性,能够有效应对ADN运行中的不确定因素,实现高效供电。

本文调度模型暂未计及无功补偿措施和电动汽车,概率潮流计算未考虑不确定变量之间的相关性。在接下来的研究过程中将予以考虑,为ADN优化调度和能量管理提供科学依据。

本文获得国网内蒙古东部电力有限公司“分布式新能源与配网协同发展体系建设及规划技术研究”项目支持,在此表示感谢。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参考文献

[1] 孙辉,沈钟浩,周玮,等.主动配电网源荷协调多目标阻塞调度[J].电力系统自动化,2017,41(16):88-95.DOI:10.7500/AEPS20170120015.

SUN Hui, SHEN Zhonghao, ZHOU Wei, et al. Multi-objective congestion dispatch of active distribution network based on source-load coordination[J]. Automation of Electric Power Systems, 2017, 41(16): 88-95. DOI: 10.7500/AEPS20170120015.

[2] 蒲天骄,陈乃仕,王晓辉,等.主动配电网多源协同优化调度架构分析及应用设计[J].电力系统自动化,2016,40(1):17-23.DOI:10.7500/AEPS20150520010.

PU Tianjiao, CHEN Naishi, WANG Xiaohui, et al. Application and architecture of multi-source coordinated optimal dispatch for active distribution network[J]. Automation of Electric Power Systems, 2016, 40(1): 17-23. DOI: 10.7500/AEPS20150520010.

[3] CALDERARO V, CONIO G, GALDI V, et al. Active management of renewable energy sources for maximizing power production[J]. International Journal of Electrical Power & Energy System, 2014, 57(5): 64-72.

[4] MOKRYANI G. Active distribution networks planning with integration of demand response[J]. Solar Energy, 2015, 122: 1362-1370.

[5] 黄伟,杨舒文,葛良军.基于概率潮流的主动配电网供需群体协同优化运行策略[J].电力系统自动化,2017,41(13):39-44.DOI:10.7500/AEPS20170116009.

HUANG Wei, YANG Shuwen, GE Liangjun. Source and load coordinated optimal operation strategy based on probabilistic load flow in ADN[J]. Automation of Electric Power Systems, 2017, 41(13): 39-44. DOI: 10.7500/AEPS20170116009.

[6] 庄慧敏,肖建.主动配电网的两阶段优化调度模型[J].西南交通大学学报,2015,50(5):928-934.

ZHUANG Huimin, XIAO Jian. Two-stage optimal schedule model for active distribution network[J]. Journal of Southwest Jiaotong University, 2015, 50(5): 928-934.

[7] 丁涛,孙宏斌,柏瑞,等.考虑最大风电容量接入的带禁止区间实时经济调度模型[J].中国电机工程学报,2015,35(4):759-765.

DING Tao, SUN Hongbin, BO Rui, et al. Real-time economic dispatch model with prohibited zones considering maximum wind power injection[J]. Proceedings of the CSEE, 2015, 35(4): 759-765.

[8] 黄伟,李宁坤,田羽洲,等.主动配电网日前-实时调度策略研究[J].现代电力,2017,34(3):52-59.

HUANG Wei, LI Ningkun, TIAN Yuzhou, et al. Research on day-head and real-time schedule strategy for ADN[J]. Modern Electric Power, 2017, 34(3): 52-59.

[9] 高雅静,李瑞环,梁海峰,等.考虑间歇性电源与负荷不确定性情况下基于多场景技术的主动配电系统两步优化调度[J].中国电机工程学报,2015,35(7):1657-1665.

GAO Yajing, LI Ruihuan, LIANG Haifeng, et al. Two step optimal dispatch based on multiple scenarios technique considering uncertainties of intermittent distributed generations and loads in the active distribution system[J]. Proceedings of the CSEE, 2015, 35(7): 1657-1665.

[10] 曾鸣,杨雍琦,向红伟,等.兼容需求侧资源的“源-网-荷-储”协调优化调度模型[J]. 电力自动化设备,2016,36(2):102-111.

ZENG Ming, YANG Yongqi, XIANG Hongwei, et al. Optimal dispatch model based on coordination between “generation-grid-load-energy storage” and demand-side resource[J]. Electric Power Automation Equipment, 2016, 36(2): 102-111.

[11] 胡泽春,王锡凡.基于半不变量法的随机潮流误差分析[J].电网技术,2009,33(18):32-37.

HU Zechun, WANG Xifan. Error analysis of the probabilistic load flow based on cumulant method[J]. Power System Technology, 2009, 33(18): 32-37.

[12] 张江林,夏榆杭,段登伟,等.基于WCVaR评估的虚拟发电厂能量市场收益——风险模型[J].电力系统自动化,2017,41(9):77-83.DOI:10.7500/AEPS20160716004.

ZHANG Jianglin, XIA Yuhang, DUAN Dengwei, et al. Benefit-risk model of virtual power plant in energy market based on WCVaR assessment[J]. Automation of Electirc Power Systems, 2017, 41(9): 77-83. DOI: 10.7500/AEPS20160716004.

[13] 曾丹,姚建国,杨胜春,等.柔性负荷与电网互动的系统动力学仿真模型[J]. 中国电机工程学报,2014,34(25):4227-4233.

ZENG Dan, YAO Jianguo， YANG Shengchun, et al. System dynamics simulation model of flexible load in intearactive power grid[J]. Proceedings of the CSEE, 2014, 34(25): 4227-4233.

[14] PRUSTY B R, JENA D. A critical review on probabilistic load flow studies in uncertainty constrained power systems with photovoltaic generation and a new approach[J]. Renewable and Sustainable Energy Reviews, 2017, 69: 1286-1302.

[15] 熊强,陈维荣,张雪霞,等.考虑多风电场相关性的场景概率潮流计算[J].电网技术,2015,39(8):2154-2159.

XIONG Qiang, CHEN Weiroong, ZHANG Xuexia, et al. Scenario probabilistic load flow calculation considering wind farms correlation[J]. Power System Technology, 2015, 39(8): 2154-2159.

[16] 李鹏,徐伟娜,周泽远,等.基于改进万有引力搜索算法的微网优化运行[J]. 中国电机工程学报,2014,34(19):3073-3079.

LI Peng, XU Weina, ZHOU Zeyuan, et al. Optimal operation of microgrid based on improved gravitational search algorithm[J]. Proceedings of the CSEE, 2014, 34(19): 3073-3079.

[17] 黄太安,生佳根,徐红洋,等.一种改进的简化粒子群算法[J]. 计算机仿真,2013,30(2):327-330.

HUANG Taian, SHENG Jiagen, XU Hongyang, et al. Improved simplified particle swarm optimization[J]. Computer Simulation, 2013, 30(2): 327-330.

[18] 尤毅,刘东,钟清,等.主动配电网优化调度策略研究[J].电力系统自动化,2014,38(9):177-183.DOI:10.7500/AEPS20130804001.

YOU Yi, LIU Dong, ZHONG Qing, et al. Research on optimal schedule strategy for active distribution network[J]. Automation of Electric Power Systems, 2014, 38(9): 177-183. DOI: 10.7500/AEPS20130804001.