电力系统运行调度中的高阶不确定性及其对策评述

周安平, 杨 明, 赵 斌, 韩学山, 刘增训

(1. 电网智能化调度与控制教育部重点实验室(山东大学), 山东省济南市 250061; 2. 国家电网有限公司, 北京市 100031)

0 引言

电力系统运行中存在着各种不确定因素,如负荷的随机扰动和发输电元件的意外停运等。近年来,随着新能源电源的广泛并网发电,其随机性、间歇性的特点进一步加剧了电力系统运行的不确定程度。电力系统调度中各类不确定问题的出现使得调度方法逐步由确定性向不确定性转变[1]。

针对确定性调度方法的不足,一方面,诸多学者通过对不确定变量的随机性建模,利用可靠性估计手段[2-3]、概率预测方法[4-9],获得不确定变量的概率分布函数,构建随机规划模型与算法,求得具有统计意义的优化调度结果[10-20]。另一方面,决策过程中仅需扰动边界信息[21-22]的鲁棒优化方法也被用来进行电力系统调度算法的设计。鲁棒优化以扰动集合表征变量的不确定性,意在制定最坏扰动情况下的最佳决策,并对多类扰动集合具有较好的计算性质。并且,通过对可接纳扰动范围边界的统筹优化,基于鲁棒优化的调度算法已可充分利用不确定变量的概率分布信息,以较小的计算代价得到与随机规划相媲美的决策效果[23-25]。上述预测、优化方法融入多时间尺度、多空间维度、多决策对象的电力系统调度实际,构成了不确定运行条件下电力系统调度理论研究的重要方向,目前仍然处于十分活跃的研究阶段。

然而,在电力系统的运行实际中,不确定变量的概率分布函数常常难以精确获取,由此,无论基于随机或是鲁棒优化方法,以精确概率为数据基础的决策理论,更多地表现为一种理性的指导思想,其决策结果对应的期望效用在现实中往往难以显现,决策的有效性受到质疑。

随着不确定运行条件下电力系统调度理论研究的不断深入,电力系统源、网、荷的动态平衡所呈现出的高阶不确定性逐步得到认识,其中不确定量概率分布自身的不确定性,即高阶不确定性(高阶指除了包括不确定量本体的不确定性,还包括对不确定量不确定规律掌握的不确定性)对于调度决策结果的有效性产生了极为重要的影响,尤其在近几年,一些针对调度理论中高阶不确定性问题的分析与决策方法,得到初步而快速的发展。

在上述背景下,本文围绕着高阶不确定性这一核心线索,针对电力系统运行调度中的源、网、荷(具体为新能源电源发电功率、负荷响应能力以及发输电设备运行可靠性)存在的高阶不确定性问题,介绍与评述目前已有的相关研究成果,并对这一研究方向中亟待解决的关键问题与未来的发展趋势进行总结与展望,以期为相关研究工作的进一步开展提供有益的参考。

1 调度决策中的高阶不确定性

理论上,高阶不确定性被定义为在一阶不确定性(不确定量自身的不确定性)基础上的、不确定量描述过程中产生的不确定性[26-27]。本文聚焦于电力系统运行调度中源、网、荷不确定量的概率描述,将上述高阶不确定性的定义具体化为对不确定量概率分布规律掌握的不确定性,其产生的原因主要包括如下两个方面。

一方面,对不确定量概率规律的挖掘,难免应用到各类统计或者预测模型,然而,任何模型在构建过程中的近似与简化都使模型难以尽善尽美,模型的不完备性是导致不确定量概率分布不确定性产生的重要因素。例如,对于风电功率的统计概率来说,从早期广泛应用的正态分布[28-29],到近期应用的β分布[30-31]、混合拉普拉斯分布[32]、柯西分布[33]、α-稳态分布[34]等,虽然采用这些预先假定的分布模型可以提高统计的效率,减少所需样本数量,但采用这些统计模型的合理性,在现实中却往往难以证明,实际上,风电功率是否服从一种已知的概率分布形式是很难回答的问题。

另一方面,数据作为不确定量分布估计或者预测的基础,其准确与否将直接关系到预测结果的有效性。然而,在电力系统的运行实际中,样本丢失、偏差、错位的情况十分普遍,数据的不准确将直接导致不确定量概率分布的高阶不确定性。风电功率的短期概率分布预测是数据导致高阶不确定性的一个很好的例子。概率预测模型通过训练建立了从输入量(解释变量)到输出量(待预测量)概率分布的映射函数,对于风电功率的概率预测来讲,风速预测值是一项很重要的输入变量,然而,风速的准确预测是不现实的,其本身就有很多可能的值,这些可能的风速将对应着不同的风电功率分布,从而导致了对风电功率概率分布预测的高阶不确定性。

上述两方面的因素往往同时存在、相互交织,导致了电力系统运行中高阶不确定性问题的普遍性。高阶不确定性会影响优化调度对于决策风险的把握,使其丧失决策的有效性,应给予必要的重视。从当前研究现状来看,在可再生能源、负荷高阶不确定性方面,现有研究主要关注于统计矩的不确定性问题,而在设备运行可靠性评估方面,当前研究则主要关注于设备故障区间概率、模糊概率的表达与获取。

2 可再生能源发电高阶不确定性研究现状

可再生能源发电的不确定性是电网调度人员关注的问题。在优化调度理论研究层面,现有方法主要针对可再生能源发电概率分布的矩不确定性问题,即随机变量矩信息,如统计均值(一阶矩)、方差(二阶矩)不确定导致的高阶不确定性问题。针对此问题的调度决策研究在模型建立、分布集合构建以及模型转换求解上的特点如下文所述。

2.1 决策模型

为更为真实地描述风力发电的统计规律,文献[35]在进行含风电电力系统最优潮流问题的研究时,考虑了风电功率概率分布的不确定性,其后发展形成了计及均值及方差(一阶矩、二阶矩)不确定性的矩不确定性机会约束最优潮流模型。其所建立的模型可泛化为[36]:

(1)

(2)

(3)

∀i∈G

(4)

∀(i,j)∈L

(5)

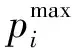
在上述模型中,目标函数式(1)表示优化的目标是使发电的期望成本最小;式(2)是限定各发电机组参与因子之和为1的约束;式(3)为系统有功功率平衡方程,保证在预期场景下发电与负荷有功功率的平衡;式(4)与式(5)为引入的鲁棒机会约束不等式,其中,式(4)是指发电机组输出功率应满足上、下限值的机会约束,式(5)为线路传输功率不超过允许限值的机会约束,其线路潮流采用直流潮流模型获得。需要特别说明的是,D表征一阶矩、二阶矩分别为μ和Σ的概率分布集合,此集合既可以假定随机向量满足某种具体的分布形式(如正态分布)而允许其矩在一定范围内变化,也可以给定矩的值而不对其分布形式做具体的假设(任何形式的分布,只要满足已知的矩条件,就包含在分布集合内,详见2.2节)。此集合描述了风电功率的不确定性程度,是此类高阶不确定性决策问题构建、分析与求解的关键。

在此之后,相继又出现了多种针对矩不确定性问题的优化调度模型。其中,文献[37]在目标函数中考虑了备用成本并给出了联合机会约束,其要求各个机会约束成立的概率下限值均相同。文献[38]在文献[35]模型的基础上,增加了发电机组输出功率调节能力的机会约束。文献[39]给出了含风电电力系统计及CO2排放的分布鲁棒经济调度模型,其在目标中考虑了CO2的排放成本。文献[40]在文献[37]单时段决策模型的基础上,发展了多时段的动态调度模型,并考虑了不同时间尺度备用间的协调问题。

2.2 分布集合的构成

基于矩不确定性机会约束规划的调度决策模型与基于机会约束规划的调度决策模型的根本区别在于引入了描述随机向量矩不确定性问题的分布集合。该集合的形式不仅会影响到分布鲁棒机会约束规划的转化与求解,更会影响到优化结果的保守程度,对解的有效性至关重要。

文献[38]假设风电功率预测误差服从独立正态分布,针对其均值与方差的不确定性,给出了多面体形式[41]的矩不确定集合,从而,对可能的误差分布集合进行了限定[42]。其矩不确定性集合表示为:

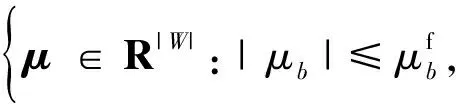
(6)

Ds=s∈R|W|:∃t:s=σ+t,|tb|≤σb,

(7)

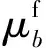
该集合在假定误差独立正态分布的前提下,将随机变量的均值与方差以区间的形式给出以表征其不确定程度,并通过设置保守系数对保守度进行限定。

文献[37,40,43-45]给出的风电功率预测误差分布集合为:

(8)

式中:f(w)为随机向量w的联合概率密度函数。

与式(6)、式(7)相比,该集合给出了风电功率预测误差均值向量与协方差矩阵的积分定义式,并赋予它们确定的值,但是,该集合设定时并不限定风电功率预测误差具体的分布形式。此集合的本质含义为:所有均值向量与协方差矩阵满足给定条件的联合概率分布都是分布集合内的元素。以此,表征了分布的不确定性。

文献[39,46-47]中随机向量的期望采用了椭球不确定集描述,协方差矩阵采用矩阵不等式限定的半定锥不确定集描述,对应表述如下:

D=

(9)

式中:γ1为期望的椭球不确定集半径的限制参数;γ2为协方差矩阵的半定锥不确定集范围的限制参数;E为期望值算子;μ0和Σ0分别为风电功率预测误差均值向量、协方差矩阵的统计值;S为随机变量的分布空间;P为求概率函数;≼为半负定符号。

不确定集合式(9)是不确定集合式(6)和式(7)与不确定集合式(8)的结合,其既没有对随机向量的具体分布形式进行限定,也允许一阶、二阶矩在一定范围内波动,因而是一种更普适的分布集合。

文献[36]给出的不确定集合为不确定集合式(8)的特殊形式,可表述为:

D={w∈S:E(w)=0,E(wwT)=Σ}

(10)

该不确定性集合要求风电功率预测误差的均值向量为0,协方差矩阵为Σ。

上述分布集合的构建主要专注于对不确定量一阶矩、二阶矩信息的描述,其概率密度函数、分布函数信息未被有效纳入决策过程,因而存在一定的保守性。而直接描述不确定量概率密度函数的分布集合往往能提供更多的信息,目前已初步应用于分布鲁棒机组组合问题[48-49],为控制调度决策模型的保守度提供了新的思路。

2.3 模型的转化与求解

对于计及矩不确定性优化调度模型的求解,其重点在于根据给定分布集合的特点,利用对偶、等价等转换方法,将原模型转化为确定性、易处理的数学优化问题。

文献[36]将模型中的鲁棒机会约束表示为如下一般形式:

(11)

式中:x为决策变量;a(x)和b(x)为x的线性函数;T为给定的常数；o为风险系数。

进而,结合式(10)给定的分布集合形式及相关数学推导,将式(11)等价转化为凸二阶锥约束形式,与之对应,原问题被转化为确定性的凸二阶锥规划(second order cone programming,SOCP)问题,从而得到快速的求解。

文献[37,40]针对多约束成立的联合概率,将模型中的鲁棒联合机会约束表达为如下所示的二次不等式形式:

(12)

式中:Lj(x)为x的线性函数;πj为常量;m为机会约束条件的数量。

而后,基于式(8)给定的不确定集合形式,采用对偶理论以及相应的数学引理,将式(12)所示约束等价转化为双线性矩阵不等式(bilinear matrix inequality,BMI)的形式,并通过求解转化后的BMI约束问题,实现了对原问题的求解,但计算效率相对较低。

文献[38]假定模型中的随机变量均满足正态分布,针对式(6)、式(7)所示的一阶矩、二阶矩的变化范围,将鲁棒机会约束转化为二次鲁棒区间约束,并通过松弛—约束检验的启发式方法,不断加入不满足的鲁棒区间约束的确定性线性化近似约束,由此,迭代求解,直到所有鲁棒区间约束均得到满足,实现对原问题的求解。模型中的各个鲁棒机会约束独立处理,算法具有较高的计算效率,但启发式算法的最优性难以得到保证。

文献[39]假设随机向量的期望与协方差符合式(9)所描述的一般性分布集合的形式,采用鲁棒优化思想构建了min-max优化模型,进而,基于拉格朗日对偶原理将决策模型转换为确定性的半定规划(semidefinite programming,SDP)问题进行求解,算法计算效率较慢。

文献[46]同样针对式(9)所示的一般性分布集合,通过数学推导,将模型中的鲁棒机会约束等价转化为确定性的一次或二次约束形式,从而,将整个模型转化为二次约束二次规划(quadratically constrained quadratic programming,QCQP)问题,再进一步,利用重构线性化技术(reformulation-linearization technique,RLT),将QCQP问题进行松驰线性化处理,转化为线性规划(linear programming,LP)问题进行求解,方法具有较高的计算效率。

不确定分布集合的选取、模型的转化与求解是构建针对矩不确定性问题的鲁棒机会约束规划方法的关键,其必将是未来研究与探讨的焦点与热点。

3 负荷响应容量高阶不确定性的研究现状

电力负荷,尤其是柔性负荷,如制热和冷却系统,可通过负荷控制技术为系统提供一定量的备用[50-55]。然而,由于负荷本身是时变且不确定的,导致了负荷响应容量的不确定。负荷响应容量概率分布的精确估计同样是难以实现的,故其亦具有高阶不确定性。当前,已有调度算法计及了负荷响应容量的高阶不确定性,其所主要应用的也是基于矩不确定性的鲁棒机会约束规划方法。从本质上讲,对于负荷响应容量高阶不确定性的处理方法与上一部分综述的对可再生能源发电高阶不确定性问题的处理方法具有相通性。

3.1 决策模型

在优化模型上,考虑负荷响应容量与风电功率高阶不确定性的决策模型是极其相似的,只在建模细节上有所区别。例如,文献[56-57]在目标函数中考虑了负荷备用成本:

(13)

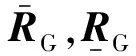
文献[56-57]在模型中定义了实时供需不平衡功率量Pm,其含义为系统中所有风电场出力预测偏差之和减去所有负荷响应功率预测偏差之和,并将该不平衡功率Pm以分配因子的形式分配至发电机和柔性负荷,以此,形成扰动后机组、柔性负荷功率调整满足允许调整范围的鲁棒机会约束不等式。同时,模型也基于直流潮流给出了线路潮流的鲁棒机会约束。值得指出的是,该文建模时同时考虑了联合鲁棒机会约束不等式和独立鲁棒机会约束不等式两种形式,即

(14)

(15)

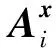
在上述鲁棒机会约束定义的基础上,文献[56-57]给出了考虑负荷响应容量矩不确定性的鲁棒机会约束最优潮流模型。

3.2 模型的转化与求解

无论是考虑负荷响应容量高阶不确定性的机会约束调度模型还是考虑新能源发电高阶不确定性的机会约束调度模型,其求解的关键均在于:针对给定的分布集合,实现鲁棒机会约束的确定性等价处理。文献[56-57]在求解考虑负荷高阶不确定性的调度模型时,除与文献[39]类似地给出了针对式(9)所示分布集合的SDP处理方法外,还介绍了几种不同思路的方法。

文献[56]针对独立机会约束,提出了一种求解半无限凸规划问题的场景采样法,该方法无需对不确定变量的概率分布形式做诸多假设,通过满足大量场景样本构造的运行约束,来保证优化结果能够以给定置信水平保证机会约束的成立。根据概率理论,参与优化的场景样本数需至少需满足[58]:

(16)

式中:Ωap为样本集合;|Ωap|为所需的样本数量;β为给定的常数,1-β为机会约束成立的置信水平[59];n′为模型中决策变量的维数。

然而,可以看到,该方法所需样本数较大,在实际应用中将受到数据及解算效率的限制。

文献[57]选取式(8)所示的分布集合形式,将式(15)所示的独立鲁棒机会约束等价转化为:

(17)

得到式(17)的等价形式后,整个模型便转换为SOCP问题进行求解。

上述基于优化技术形成的高阶不确定性处理方法,无论是对于新能源发电功率还是对于负荷响应容量的高阶不确定性,关注的重点均在于优化模型的构建和算法的设计,其分布集合的建立相对粗糙,尚缺乏对样本信息的充分挖掘及与预测过程的有机结合。因而,上述优化方法虽然给出了分布不确定条件下调度决策在优化算法层面的参考,但其决策结果仍可能处于保守与冒进的两难境地。

4 设备故障高阶不确定性的研究现状

电力设备作为电力系统构成的基本元素,其发生故障[60-61]将导致系统拓扑结构的改变,破坏系统功率平衡,引发潮流转移,降低系统运行的安全性与经济性,是电力系统调度运行中需要关注的重要不确定因素。传统上,电力设备故障概率通常被假定为固定值,并以长期统计平均值来替代。然而,恒定的平均故障概率指标难以有效描述设备故障概率随运行条件改变而变化的特性。实际上,对电力设备给定工况下停运概率指标的估计,可归纳为对状态离散随机变量条件概率分布函数的预测问题[62]。

在实际系统中,由于可用样本少、外部环境信息不完全等因素,对设备故障概率的估计存在较为明显的误差,导致设备故障呈现出高阶不确定性。当前,常用区间与模糊两类方法来描述设备故障概率的不确定性。

区间概率[63-64]是一类常用的高阶不确定性的描述方法,对于电力设备,其故障的区间概率可表示为:

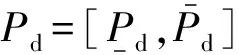
(18)

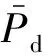
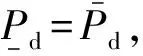
目前,对于设备故障的区间概率,已有了相当数量的研究。文献[65]考虑了不同天气状况对架空配电线路停运率及配电系统可靠性的影响,分别基于泊松回归模型及贝叶斯网络模型建立了架空配电线路的故障率模型,并运用中心极限定理估计得到了上述两种模型架空线路故障率的置信区间,然而,当样本数量过少时,该方法难以得到可靠的估计结果。文献[66]在电力设备故障样本缺失、不充足的情况下,以非精确概率理论中的伽马指数模型构造了设备无故障工作时间和故障修复时间的概率箱[67],对电力设备稳态可用度(即设备处于可用状态的概率)的区间进行了统计推断,取得了良好的效果。其基于伽马指数模型求取的稳态可用度区间表示为:

(19)

(20)

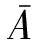
文献[66]研究针对设备长期运行可靠性问题,并没有体现短期内设备停运概率随运行工况变化而时变的特点。

文献[68]基于输电线路停运的历史统计数据和估计目标时段的运行工况,构建了处理非精确条件概率推断问题的信度网络,对输电线路停运的条件区间概率进行估计。其所构建的信度网络见图1。

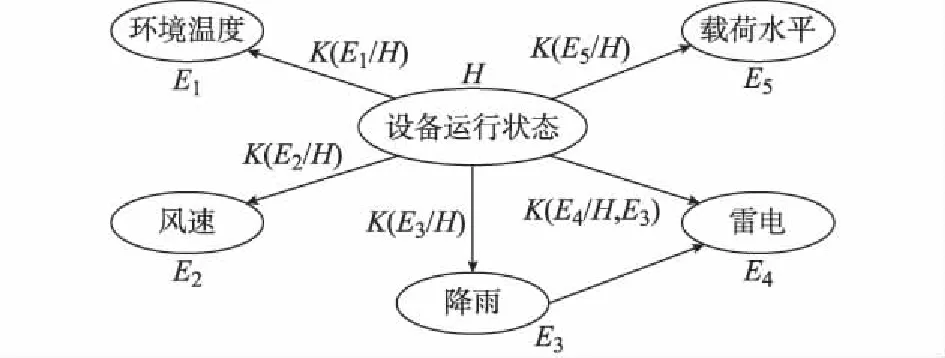
图1 设备停运概率估计信度网络Fig.1 Credal networks of component outage probability

在图1所示的信度网络中,E1,E2,E3,E4,E5为线路运行工况的随机(证据)变量;H为线路运行状态的随机变量;K(·)为条件信度集。该方法利用多状态随机变量的非精确狄利克雷模型,获得了信度网络节点的条件区间概率。其中,多状态非精确狄利克雷模型可表示为:

(21)

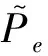
该方法体现了电力设备停运概率依其运行工况变化而时变的特点,为解决停运样本缺乏条件下的电力设备运行可靠性评估问题提供了新的思路。

在系统层面,文献[69-70]基于区间数运算法则建立了配电系统可靠性评估的区间估计模型,在已知设备各状态区间概率的基础上,对多种系统可靠性指标(如系统平均停电频率)进行了区间估计。

文献[71]采用非精确狄利克雷模型获得电力设备各状态的区间概率,进而,基于仿射运算法则[72]给出了系统可靠性的仿射区间估计方法。其所给出的系统可靠性指标的仿射形式可表示为:

(22)

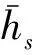
文献[71]利用式(22)得到多状态系统可靠性指标更为准确的区间估计结果,具有借鉴意义。

除了区间概率,模糊变量[73]也常被用来表征设备状态的高阶不确定性。文献[74]将架空线路处于某一状态的概率用模糊数表示,定义架空线路的故障风险指标为:

(23)

式中:Ri(t)为第i条线路t时刻的风险指标;s表示线路的运行状态,s=0为正常运行状态,s=1为瞬时故障状态,s=N为永久故障状态;Pis(t)为第i条线路t时刻处于状态s的概率;Sis(t)为对应的状态严重性指标(线路过载等)。

式(23)中,Pis(t)和Sis(t)均被设为三角模糊变量,其隶属度函数可表示为:

(24)

式中:u(x)为三角模糊变量x的隶属度函数;xmax,xavg,xmin分别为三角模糊变量x的上限值、平均值及下限值。

在得到上述架空线路故障的风险指标后,文献[74]基于随机过程停运模型[75]和可信性理论[76]建立了模糊故障率下的设备停运模型,为解决缺乏历史统计数据情况下的设备故障问题提供了思路。

文献[77]视线路修复时间、设备故障率为三角模糊变量,并依据标准正态分布置信区间估计方法、泊松分布均值置信区间估计方法得到上述两种指标的区间,进而,构建出相应的隶属度函数。文中同时考虑了不同天气情况对设备可靠性指标的影响。以设备故障率为例,电力设备在不同天气情况下的等效故障率可表示为:

λE=λNR+λA(1-R)

(25)

式中:λE为设备故障的等效故障率;λN和λA分别为在正常、不正常天气情况下估计得到的设备故障率;R为正常天气情况占总天气情况的概率估计值。λN,λA,R均为模糊变量。

文献[78]提出了一种模糊多状态系统的可靠性评估模型。其假定文中模糊变量均为三角模糊变量,介绍了模糊多状态系统的基本定义及假设,并通过定义相关性、一致性及等效性来表征此类模糊多状态系统的特征,取得了良好的效果。

设备故障概率隶属于离散型不确定量,由于样本数量的缺乏以及受设备运行可靠性内、外部运行工况的影响显著,其概率分布函数获取极为不易,区间数、模糊数方法能较为全面地描述设备故障的高阶不确定性,以此区别于新能源、负荷此类连续型不确定量以概率密度函数、矩信息(也即分布集合)表征其高阶不确定性;此外,就目前而言,设备故障概率的高阶不确定性研究多限于描述过程,在实际电力系统运行调度中还尚鲜有涉及。其中,文献[79]提出了一种针对机组故障导致高阶不确定性的分布鲁棒优化方法,构建了描述机组故障概率的不同模糊集合,并采用Benders分解算法对所提模型进行求解,值得关注。

5 问题及展望

安全、可靠与经济运行是电力系统调度所追求的目标。随着电力市场化改革的推进、可再生能源并网发电比例的提高,调度对于运行中的不确定性问题给予了极大的关注,计及运行中各类不确定因素的调度方法在理论与实践两个层面均得到了显著的发展。而随着研究的深入,研究焦点逐步从不确定量随机规律的挖掘、表达与利用,过渡到对随机规律自身高阶不确定性特征的挖掘、表达与利用,这是符合科学研究发展的客观规律的。与此同时,由于随机规律的高阶不确定性对于调度决策结果的有效性有着直接而显著的影响,相关研究也是现实中所迫切需要的,有着明显的工程应用价值。

然而,针对随机变量概率分布规律的高阶不确定性问题,其分析更为抽象、建模与求解更为困难,即使是在理论层面,当前也仍处于研究的初级阶段。根据相关研究经验,结合广泛的文献查阅、研读和思考,对于电力系统调度中高阶不确定性特征的挖掘、表达与利用,至少存在如下尚待解决的问题。

1)缺乏与源、荷功率预测技术相匹配的高阶不确定性规律的挖掘与利用方法。在源、荷的功率预测方面,针对预测误差规律挖掘的概率预测技术已经广为电力工作者所熟知。概率预测所得到的概率分布自身的误差即体现出高阶不确定性。然而,从当前概率预测的研究来看,虽然其在充分挖掘数据信息、提高概率分布预测精度方面有了显著的进步,但在分布预测结果误差的度量方面,相关指标还不能够与高阶不确定性的优化决策方法相融合。换言之,现有概率预测优劣的评价指标无法被高阶不确定性决策方法所直接利用,同时,高阶不确定性的决策方法,往往忽略了概率预测环节,未能给出结合概率预测偏差范围进行决策的有效途径。

2)电力设备故障的高阶不确定性未被有效计入电力系统调度的决策过程。考虑事故备用的概率调度方法目前已被广泛采纳,然而,不管是采用何种随机性优化决策方法(如期望值模型、机会约束规划模型),其均假设设备的故障概率可以精确获知。然而,正如前述研究所指出的,故障概率极难被准确地预测,因而,基于精确故障概率的概率性调度决策方法,往往会导致保守或冒进的决策结果,丧失决策的有效性。在现有设备故障区间概率、模糊概率估计的基础上,如何发展相应的调度决策方法,是目前尚待解决的问题。

3)计算困难仍是制约高阶不确定性问题解决的关键。从模型构建与求解的角度来讲,考虑可再生能源发电不确定性、设备故障不确定性的概率调度问题本身就已十分困难,当叠加上概率分布自身的不确定性,使得问题更加复杂,其模型转换与算法构建不仅对于电力工作者来讲十分困难,甚至在数学分析与优化领域,也是具有挑战性的问题。因此,结合电力系统优化调度本身特点,针对相应模型构建合适的转化与求解算法,使其具有问题求解上的可行性,是解决高阶不确定性问题的关键。

4)计及高阶不确定性的成本/风险分析尚待进一步深入开展。在不确定运行条件下,电力系统的决策必然是运行风险与风险防范代价的折中。在传统的概率调度中,风险被定义为事件发生概率与事件后果的乘积,其可以被估计出来并与风险防范成本相比较。然而,当概率分布类型、概率分布参数自身不准确时,上述比较必将发生改变。面对概率分布的高阶不确定性,如何选择需要考虑的分布集合、如何计算运行风险以及如何与风险防范成本相折中,都是需要进一步深入探讨的问题。

上述问题的解决必然是一个系统工程,无法诉诸单一环节、单一模型或者单一算法的独立进展。其解决必然需要基于数据,通过功率预测、功率分布预测、功率分布预测偏差估计等一系列的数据挖掘环节,实现对于可信分布集合的建立。进而,基于针对矩不确定性、概率分布集合、模糊概率分布的优化方法,结合电力调度的实际情况,建立相应的调度模型及其转化与求解方法,实现调度的优化决策。很显然,上述各个环节均是充满挑战的,需要大量的研究工作来完成与实现。

总之,在电力系统调度理论由确定性向不确定性转变的过程中,应现代电力系统运行特点与数据特征的需求,开展切实可行的预测、决策相协调的电力系统高阶不确定运行条件下的调度理论与方法研究,具有突出的必要性与紧迫性,必然会成为调度理论研究中重要的研究方向。

参考文献

[1] 杨明,韩学山,王士柏,等.不确定运行条件下电力系统鲁棒调度的基础研究[J].中国电机工程学报,2011,31(增刊1):100-107.

YANG Ming, HAN Xueshan, WANG Shibai, et al. Fundamental research for power system robust dispatch under uncertain operating condition[J]. Proceedings of the CSEE, 2011, 31(Supplement 1): 100-107.

[2] 何剑,程林,孙元章,等.条件相依的输变电设备短期可靠性模型[J].中国电机工程学报,2009,29(7):39-46.

HE Jian, CHENG Lin, SUN Yuanzhang, et al. Condition dependent short-term reliability models of transmission equipment[J]. Proceedings of the CSEE, 2009, 29(7): 39-46.

[3] 宁辽逸,吴文传,张伯明.电力系统运行风险评估中元件时变停运模型分析[J].电力系统自动化,2009,33(16):7-12.

NING Liaoyi, WU Wenchuan, ZHANG Boming. Analysis of a time-varying power component outage model for operation risk assessment[J]. Automation of Electric Power Systems, 2009, 33(16): 7-12.

[4] PINSON P, KARINIOTAKIS G. Conditional prediction intervals of wind power generation[J]. IEEE Transactions on Power Systems, 2010, 25(4): 1845-1856.

[5] 王松岩,于继来.风速与风电功率的联合条件概率预测方法[J].中国电机工程学报,2011,31(7):7-14.

WANG Songyan, YU Jilai. Joint conditions probability forecast method for wind speed and wind power[J]. Proceedings of the CSEE, 2011, 31(7): 7-14.

[6] YANG Ming, SHU Fan, LEE W J. Probabilistic short-term wind power forecast using componential sparse Bayesian learning[J]. IEEE Transactions on Industry Applications, 2013, 49(6): 2783-2792.

[7] 丁华杰,宋永华,胡泽春,等.基于风电场功率特性的日前风电预测误差概率分布研究[J].中国电机工程学报,2013,33(34):136-144.

DING Huajie, SONG Yonghua, HU Zechun, et al. Probability density function of day-ahead wind power forecast errors based on power curves of wind farms[J]. Proceedings of the CSEE, 2013, 33(34): 136-144.

[8] ZHANG Yao, WANG Jianxue, WANG Xifan, et al. Review on probabilistic forecasting of wind power generation[J]. Renewable and Sustainable Energy Reviews, 2014, 32(1): 255-270.

[9] WAN Can, XU Zhao, PINSON P. Probabilistic forecasting of wind power generation using extreme learning machine[J]. IEEE Transactions on Power Systems, 2014, 29(3): 1033-1044.

[10] GOOI H B, MENDES D P, BELL K R W, et al. Optimal scheduling of spinning reserve[J]. IEEE Transactions on Power Systems, 1999, 14(4): 1485-1490.

[11] BOUFFARD F, GALIANA F D. An electricity market with a probabilistic spinning reserve criterion[J]. IEEE Transactions on Power Systems, 2004, 19(1): 300-307.

[12] WANG M Q, GOOI H B, CHEN S X. Optimizing probabilistic spinning reserve using an analytical expected energy not supplied formulation[J]. IET Generation, Transmission & Distribution, 2011, 5(7): 772-780.

[13] 查浩,韩学山,杨朋朋.电网运行状态下的概率优化调度[J].中国电机工程学报,2008,28(28):54-60.

ZHA Hao, HAN Xueshan, YANG Pengpeng. Probabilistic optimal dispatching under operating condition of power network[J]. Proceedings of the CSEE, 2008, 28(28): 54-60.

[14] 杨明,韩学山,梁军,等.计及用户停电损失的动态经济调度方法[J].中国电机工程学报,2009,29(31):103-108.

YANG Ming, HAN Xueshan, LIANG Jun, et al. Novel solution to dynamic economic dispatch considering customer interruption costs[J]. Proceedings of the CSEE, 2009, 29(31): 103-108.

[15] WANG Jianxue, WANG Xifan, WU Yang. Operating reserve model in the power market[J]. IEEE Transactions on Power Systems, 2009, 20(1): 223-229.

[16] 杨明,韩学山,杨朋朋,等.求解概率动态调度问题的Benders分解算法[J].电力系统自动化,2011,35(6):34-39.

YANG Ming, HAN Xueshan, YANG Pengpeng, et al. A novel benders decomposition based algorithm for solving probabilistic dynamic dispatch problems[J]. Automation of Electric Power Systems, 2011, 35(6): 34-39.

[17] 孙元章,吴俊,李国杰,等.基于风速预测和随机规划的含风电场电力系统动态经济调度[J].中国电机工程学报,2009,29(4):41-47.

SUN Yuanzhang, WU Jun, LI Guojie, et al. Dynamic economic dispatch considering wind power penetration based on wind speed forecasting and stochastic programming[J]. Proceedings of the CSEE, 2009, 29(4): 41-47.

[18] 江岳文,陈冲,温步瀛.含风电场的电力系统机组组合问题随机模拟粒子群算法[J].电工技术学报,2009,24(6):129-137.

JIANG Yuewen, CHEN Chong, WEN Buying. Particle swarm research of stochastic simulation for unit commitment in wind farms integrated power system[J]. Transactions of China Electrotechnical Society, 2009, 24(6): 129-137.

[19] ZHOU Wei, PENG Yu, SUN Hui. Optimal wind-thermal coordination dispatch based on risk reserve constraints[J]. European Transactions on Electrical Power, 2011, 21(1): 740-756.

[20] FABBRI A, ROMAN T G S, ABBAD J R, et al. Assessment of the cost associated with wind generation prediction errors in a liberalized electricity market[J]. IEEE Transactions on Power Systems, 2005, 20(3): 1440-1446.

[21] 周松林,茆美琴,苏建徽.风电功率短期预测及非参数区间估计[J].中国电机工程学报,2011,31(25):10-16.

ZHOU Songlin, MAO Meiqin, SU Jianhui. Short-term forecasting of wind power and non-parametric confidence interval estimation[J]. Proceedings of the CSEE, 2011, 31(25): 10-16.

[22] 郭钰锋,孙頔,于继来,等.集对分析理论在风电场风速区间预测中的应用[J].电力系统自动化,2014,38(2):6-11.DOI:10.7500/AEPS201209037.

GUO Yufeng, SUN Di, YU Jilai, et al. Application of set pair analysis in wind speed interval prediction for wind farms[J]. Automation of Electric Power Systems, 2014, 38(2): 6-11.DOI: 10.7500/AEPS201209037.

[23] WANG Cheng, LIU Feng, WANG Jianhui, et al. Robust risk-constrained unit commitment with large-scale wind generation: an adjustable uncertainty set approach[J]. IEEE Transactions on Power Systems, 2017, 32(1): 723-733.

[24] 于丹文,杨明,韩学山,等.计及风电概率分布特征的鲁棒实时调度方法[J].中国电机工程学报,2017,37(3):727-737.

YU Danwen, YANG Ming, HAN Xueshan, et al. Robust real-time dispatch considering probabilistic distribution of wind generation[J]. Proceedings of the CSEE, 2017, 37(3): 727-737.

[25] LI Zhigang, WU Wenchuan, ZHANG Boming, et al. Adjustable robust real-time power dispatch with large-scale wind power integration[J]. IEEE Transactions on Sustainable Energy, 2015, 6(2): 357-368.

[26] WANG Pei. Confidence as higher-order uncertainty[C]// Proceedings of the Second International Symposium on Imprecise Probabilities and their Applications, May 26-29, 2001, Ithaca, USA.

[27] WEINSTEIN J, YILDIZ M. Impact of higher-order uncertainty[J]. Games & Economic Behavior, 2007, 60(1): 200-212.

[28] BOUFFARD F, GALIANA F D. Stochastic security for operations planning with significant wind power generation[J]. IEEE Transactions on Power Systems, 2008, 23(2): 306-316.

[29] ALBADI M H, EL-SAADANY E F. Comparative study on impacts of wind profiles on thermal units scheduling costs[J]. IET Renewable Power Generation, 2011, 5(1): 26-35.

[30] LUIG A, BOFINGER S, BEYER H G. Analysis of confidence intervals for the prediction of regional wind power output[C]// Proceedings of the European Wind Energy Association Conference, January, 2001, Copenhagen: 725-728.

[31] FABBRI A, ROMAN T G S, ABBAD J R, et al. Assessment of the cost associated with wind generation prediction errors in a liberalized electricity market[J]. IEEE Transactions on Power Systems, 2005, 20(3): 1440-1446.

[32] TEWARI S, GEYER C J, MOHAN N. A statistical model for wind power forecast error and its application to the estimation of penalties in liberalized markets[J]. IEEE Transactions on Power Systems, 2011, 26(4): 2031-2039.

[33] HODGE B, MILLIGAN M. Wind power forecasting error distributions overmultiple timescales[C]// IEEE Power and Energy Society General Meeting, July 24-29, 2011, Detroit, USA: 8p.

[34] BRUNINX K, DELARUE E. A statistical description of the error on wind power forecasts for probabilistic reserve sizing[J]. IEEE Transactions Sustainable Energy, 2014, 5(3): 995-1002.

[35] BIENSTOCK D, CHERTKOV M, HARNETT S. Chance-constrained optimal power flow: risk-aware network control under uncertainty[J]. SIAM Review, 2014, 56(3): 461-495.

[36] XIE Weijun, SHABBIR A. Distributionally robust chance constrained optimal power flow with renewables: a coic reformulation[J]. IEEE Transactions on Power Systems, 2018， 33(2)： 1860-1867.

[37] BIAN Qianyan, XIN Huanhai, WANG Zhen, et al. Distributionally robust solution to the reserve scheduling problem with partial information of wind power[J]. IEEE Transactions on Power Systems, 2015, 30(5): 2822-2823.

[38] LUBIN M, DVORKIN Y, BACKHAUS S. A robust approach to chance constrained optimal power flow with renewable generation[J]. IEEE Transactions on Power Systems, 2016, 31(5): 3840-3849.

[39] 周任军,闵雄帮,童小娇,等.电力环保经济调度矩不确定分布鲁棒优化方法[J].中国电机工程学报,2015,35(13):3248-3256.

ZHOU Renjun, MIN Xiongbang, TONG Xiaojiao, et al. Distributional robust optimization under moment uncertainty of environmental and economic dispatch for power system[J]. Proceedings of the CSEE, 2015, 35(13): 3248-3256.

[40] WANG Zhen, BIAN Qiaoyan, XIN Huanhai, et al. A distributionally robust co-ordinated reserve scheduling model considering CVaR-based wind power reserve requirements[J]. IEEE Transactions on Sustainable Energy, 2016, 7(2): 625-636.

[41] LI Zukui, FlOUDAS C A. Robust counterpart optimization: uncertainty sets, formulations and probabilistic guarantees[C]// Proceedings of the 6th Conference on Foundations of Computer-Aided Process Operations, 2012, Savannah, Georgia: 6p.

[42] BERTSIMAS D, SIM M. The price of robustness[J]. Operations Research, 2004, 52(1): 33-53.

[43] DELAGE E, YE Y. Distributionally robust optimization under moment uncertainty with application to data-driven problems[J]. Operations Research, 2010, 58(3): 595-612.

[44] JIANG Ruiwei, GUAN Yongpeng. Data-driven chance constrained stochastic program[J]. Mathematical Programming, 2016, 158(1/2): 291-327.

[45] ZYMLER S, KUHN D, RUSTEM B. Distributionally robust joint chance constraints with second-order moment information[J]. Mathematical Programming, 2013, 137(1/2): 167-198.

[46] ZHOU Anping, YANG Ming, WANG Zhaoyu. A linear solution method of generalized robust chance constrained real-time dispatch[J/OL]. IEEE Transactions on Power Systems[2018-01-11]. http://arxiv.org/abs/1801.03652.

[47] ZHANG Yiling, JIANG Ruiwei, SHEN Siqian. Distributionally robust chance-constrained bin packing[EB/OL]. [2016-09-30].http://paperuri:(ca025503be14b946d43dbe6155aa8630).

[48] CHEN Yuwei, GUO Qinglai, SUN Hongbin, et al. A distributionally robust optimization model for unit commitment based on Kullback-Leibler divergence[J/OL]. IEEE Transactions on Power Systems[2018-01-23]. http://ieeexplore.ieee.org/document/8267333/.

[49] DUAN Chao, JIANG Lin, FANG Wanliang, et al. Data-driven affinely adjustable distributionally robust unit commitment[J]. IEEE Transactions on Power Systems, 2018, 33(2): 1385-1398.

[50] CALLAWAY D. Tapping the energy storage potential in electric loads to deliver load following and regulation, with application to wind energy[J]. Energy Conversion and Management, 2009, 50(5): 1389-1400.

[51] BASHASH S, FATHY H. Modeling and control of aggregate air conditioning loads for robust renewable power management[J]. IEEE Transactions on Control Systems Technology, 2013, 21(4): 1318-1327.

[52] MATHIEU J, KOCH S, CALLAWAY D. State estimation and control of electric loads to man-age real-time energy imbalance[J]. IEEE Transactions on Power Systems, 2013, 28(1): 430-440.

[53] ZHANG Wei, LIAN Jianming, CHANG Chinyao, et al. Aggregated modeling and control of air conditioning loads for demand response[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4655-4664.

[54] BRASLAVSKY J, PERFUMO C, WARD J. Model-based feedback control of distributed air-conditioning loads for fast demand-side ancillary services[C]// Proceedings of IEEE Conference on Decision and Control, December 10-13, 2013, Florence, Italy: 6274-6279.

[55] MEYN S, BAROOAH P, BUSIC A, et al. Ancillary service to the grid using intelligent deferrable loads[J]. IEEE Transactions on Automatic Control, 2015, 60(11): 2847-2862.

[56] ZHANG Yiling, SHEN Siqian, MATHIEU J. Data-driven optimization approaches for optimal power flow with uncertain reserves from load control[C]// Proceedings of the American Control Conference (ACC), July 1-3, 2015, Chicago, USA: 5p.

[57] ZHANG Yiling, SHEN Siqian, MATHIEU J. Distributionally robust chance-constrained optimal power flow with uncertain renewables and uncertain reserves provided by loads[J]. IEEE Transactions on Power Systems, 2017, 32(2): 1378-1388.

[58] CAMPI M, CALAFIORE G, PRANDINI M. The scenario approach for systems and control design[C]// Proceedings of the World Congress, July 6-11, 2008, Seoul, Korea: 381-389.

[59] CAMPI M C, GARATTI S. The exact feasibility of randomized solutions of robust convex programs[J]. SIAM Journal on Control and Optimization, 2008, 19(3): 1211-1230.

[60] 刘海涛,程林,孙元章,等.基于实时运行条件的元件停运因素分析与停运率建模[J].电力系统自动化,2007,31(7):6-11.

LIU Haitao, CHENG Lin, SUN Yuanzhang, et al. Outage factors analysis and outage rate model of components based on operating conditions[J]. Automation of Electric Power Systems, 2007, 31(7): 6-11.

[61] 刘海涛,程林,孙元章,等.采用瞬时概率的运行可靠性短期评估[J].中国电机工程学报,2008,28(13):20-25.

LIU Haitao, CHENG Lin, SUN Yuanzhang, et al. Short-term operational reliability evaluation by using time dependent state probability[J]. Proceedings of the CSEE, 2008, 28(13): 20-25.

[62] YANG Ming, WANG Jianhui, DIAO Haoran, et al. Interval estimation for conditional failure rates of transmission lines with limited samples[J/OL]. IEEE Transactions on Smart Grid[2016-10-17]. http://paperuri:(dbbfce3a9b741982bbf ddf9ea830beee).

[63] 齐先军,汪兴强,黄祥玉.考虑区间概率的发输电系统非精确可靠性评估[J].电网技术,2014,38(5):1203-1209.

QI Xianjun, WANG Xingqiang, HUANG Xiangyu. Imprecise reliability assessment of composite generation-transmission system considering interval probability[J]. Power System Technology, 2014, 38(5): 1203-1209.

[64] QI Xianjun, CHENG Qiao. Imprecise reliability assessment of generating systems involving interval probability[J]. IET Generation Transmission & Distribution, 2017, 11(17): 4332-4337.

[65] ZHOU Yujia, PAHWA A, YANG S S. Modeling weather-related failures of overhead distribution lines[J]. IEEE Transactions on Power Systems, 2006, 21(4): 1683-1690.

[66] 齐先军,史新红,丁明,等.电力系统元件稳态可用度的非精确统计推断[J].中国电机工程学报,2014,34(13):2108-2115.

QI Xianjun, SHI Xinhong, DING Ming, et al. Imprecise statistical inference for steady-state availability of components in power systems[J]. Proceedings of the CSEE, 2014, 34(13): 2108-2115.

[67] UTKIN L V, KOZINE I. On new cautious structural reliability models in the framework of imprecise probabilities[J]. Structural Safety, 2010, 32(6): 411-416.

[68] 刁浩然,杨明,韩学山,等.电力设备停运概率的非精确条件估计[J].中国电机工程学报,2016,36(19):5134-5144.

DIAO Haoran, YANG Ming, HAN Xueshan, et al. Imprecise estimation for conditional outage probabilities of power components[J]. Proceedings of the CSEE, 2016, 36(19): 5134-5144.

[69] ZHANG Peng, WANG Haizhen. Interval mathematics based large-scale distribution system reliability analysis[C]// Proceedings of International Conference on Power System Technology, October 13-17, 2002, Kunming, China: 6p.

[70] 张鹏,王守相.大规模配电系统可靠性评估的区间算法[J].中国电机工程学报,2004,24(3):77-84.

ZHANG Peng, WANG Shouxiang. A novel interval method for reliability evaluation of large scale distribution system[J]. Proceedings of the CSEE, 2004, 24(3): 77-84.

[71] LI Chunyang, CHEN Xun, YI Xiaoshan, et al. Interval-valued reliability analysis of multi-state systems[J]. IEEE Transactions on Reliability, 2011, 60(1): 323-330.

[72] de GRAUWE D, LOMBAERT G, de ROECK G. Improving interval analysis in finite element calculations by means of affine arithmetic[J]. Computers and Structures, 2010, 88(3/4): 247-254.

[73] LI Wenyuan, ZHOU Jiaqi, XIE Kaigui, et al. Power system risk assessment using a hybrid method of fuzzy set and Monte Carlo simulation[J]. IEEE Transactions on Power Systems, 2008, 23(2): 336-343.

[74] 宁辽逸,吴文传,张伯明,等.运行风险评估中缺乏历史统计数据时的元件停运模型[J].中国电机工程学报,2009,29(25):26-31.

NING Yiliao, WU Wenchuan, ZHANG Boming, et al. Component outage modeling method for operation risk assessment with limited power components’ failure data[J]. Proceedings of the CSEE, 2009, 29(25): 26-31.

[75] 周孝信,郭剑波,孙元章.大型互联电网运行可靠性基础研究(II)[M].北京:清华大学出版社,2008:93-103.

[76] LIU Baoding. Uncertainty theory: an introduction to its axiomatic foundations[M]. Berlin: Springer-Verlag, 2004: 1-5.

[77] LI Wenyuan, ZHOU Jiaqi, XIONG Xiaofu. Fuzzy models of overhead power line weather-related outages[J]. IEEE Transactions on Power Systems, 2008, 23(3): 1529-1531.

[78] DING Y, ZUO M J, LISNIANSKI A, et al. Fuzzy multi-stage system: general definitions and performance assessment[J]. IEEE Transactions on Reliability, 2008, 57(4): 589-594.

[79] ZHAO Chaoyue, JIANG Ruiwei. Distributionally robust contingency-constrained unit commitment[J]. IEEE Transactions on Power Systems, 2018, 33(1): 94-102.