基于Pade近似的广域电力系统关键模态时滞轨迹分析

聂永辉， 张鹏宇， 马彦超， 张艺川， 方彬彬， 吕大朋

(1． 东北电力大学教务处， 吉林省吉林市 132012； 2． 东北电力大学电气工程学院， 吉林省吉林市 132012)

0 引言

随着电网的扩大和送电功率的增加，区间振荡问题已成为影响互联系统安全稳定运行的最重要的因素之一[1-2]。传统利用转子转速或有功功率等局部信息，传统的电力系统稳定器(PSS)反馈控制能有效地抑制局部振荡模态，但对区间振荡模态的控制效果大大降低甚至失效，那是由于发电机本地局部信号对区间振荡模态不可控或不可观测性造成的。随着相量测量单元(PMU)和广域测量系统(WAMS)的出现和发展，可为PSS控制获取区域间的发电机相对转子角和转子角速度等全局反馈信息，这些全局信息对区间振荡模态具有最大的可观测性，这为大规模电力系统区间低频振荡抑制创造了条件[3-5]。但广域信号具有高达几十毫秒到数百毫秒的传输时滞，广域信号传输时滞的引入在产生新模态的同时，其滞后相位特性将改变原有模态的阻尼比，使其可能进入右半平面，严重恶化控制器的阻尼性能[6-8]。文献[9]证明时滞控制系统分布在右半平面的特征值为有限个，因此探索时滞对电力系统关键模态和时滞相关模态的时滞影响规律，分析影响系统稳定的关键因素，对电力系统阻尼控制器设计具有重要的理论意义。

探究时滞对系统稳定性影响的方法主要包括三类[10]：时域仿真法、基于Lyapunov理论的方法和频域法的分析方法。其中第3种方法是将理论上已发展比较完善的线性系统稳定性分析理论推广到线性时滞系统。由于它可以深入揭示线性时滞系统的一些内在规律，在一定意义上指导时滞系统控制器设计，因此科技工作者对此做了一些研究工作，由此形成了诸多实用方法，包括Pade近似法[11-13]、扫频法[14-15]、基于纯虚特征根的多项式变换或转化法[16-17]。文献[10]给出了一种利用预测—校正思路的时滞电力系统全特征谱追踪算法；文献[13]采用Pade逼近法近似广域控制引进的时滞环节，进而分析了时延对其性能的影响规律，并最后应用线性最优方法确定了区间阻尼控制器控制参数；文献[16]利用Rekasius变换替换指数项，从而将时滞系统的特征方程由一个超越方程变换为普通多项式，之后利用Routh判据确定时滞系统稳定裕度；文献[17]利用共轭虚根所满足的特征方程消去该方程所含的指数项，无需中间的变量变换，从而将超越方程转化为多项式方程并求解系统的纯虚特征根，然后求解单时滞电力系统的时滞稳定裕度。

这些方法在时滞大小对大规模电力系统区间振荡模态的影响规律方面还缺乏有效的研究。本文在建立考虑时滞环节的大规模电力系统区间振荡广域控制模型的基础上，研究时滞大小对电力系统关键模态的影响规律，从而对大规模电力系统广域阻尼控制设计提供科学依据。

1 考虑时滞影响的多机系统线性化控制模型

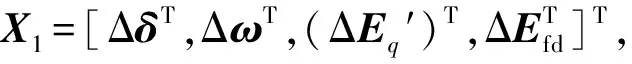
(1)

式中：ωs为同步电机角速度；ΔPm为发电机机械功率变化量，线性化后ΔPm=0；ΔPe为电磁功率变化量；D为阻尼系数；Td0′为d轴开路暂态时间常数；TJ为发电机惯性时间常数；Ka和Ta分别为励磁系统综合放大环节的增益和时间常数；ΔEq′为暂态电抗后的q轴电势变化量；Efd为同步机空载时的定子电压；Xd和Xd′分别为d轴同步、暂态电抗；Xq为q轴同步电抗；Vd和Vq分别为d轴、q轴电压；Id和Iq分别为d轴、q轴电流；Vt为发电机机端电压。

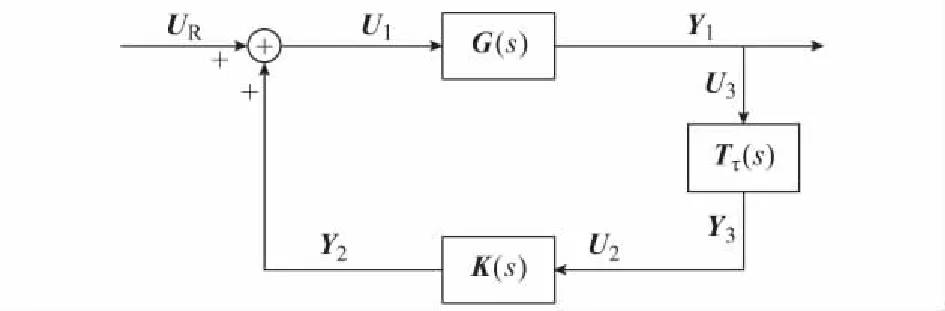
图1 计及时滞环节的闭环控制系统方框图Fig.1 Block diagram of closed-loop control system considering time delay

所有变量为适当维数的对角矩阵或向量且满足乘法运算规则，式(1)可整理为:

(2)

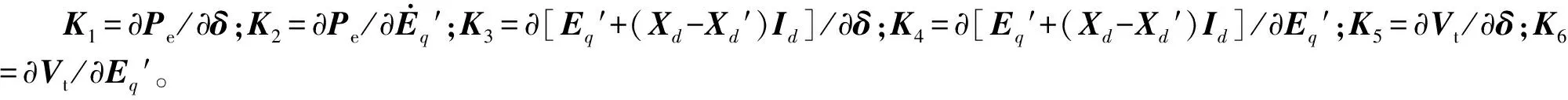
当利用发电机转速差作为广域反馈测量信号时，G(s)输出方程为：

Y1=Δω= [Δω1Δω2… Δωn]T=

[0E00]X1

(3)

式中：E为适维单位矩阵。

设控制器K(s)为广域反馈PSS，利用第i台机组的速度差信号Δωi对某台机组构成广域反馈回路时，控制器输入为速度差信号经时滞环节后的输出为Δωitd，控制器输出为ΔVs，当取广域反馈PSS状态变量为X2=[ΔV1,ΔV2,ΔV3,ΔVs]T时，可得广域反馈控制器的状态空间表达式为：

(4)

式中：KS为PSS放大倍数；T1至T6为时间常数。

电力系统采用广域测量信号构成反馈控制时,必然会产生一定数量大小的时滞。研究表明，当控制系统含有时滞时，控制效果将会急剧恶化甚至引起系统失稳。如图1中，U2与Y1间存在时延环节，在拉普拉斯域中，时延环节可用e-τs表示，而包含时滞环节e-τs的控制系统是一个无穷维系统，这给闭环系统特征值求解和控制器设计带来极大不便，本文采用Pade近似方法，将时滞项近似表达为有限维多项式[11-12]：

(5)

(6)

式中：l和k为Pade近似阶数，阶数越大，P(s)越接近于e-sτ，通常情况下，取l=k。

Pade近似过程相当于对纯时延环节进行滤波处理，传输时延数值越小，二者一致相位区间越大，即滤波频带越宽，时滞近似程度越高。对于实际电力系统，其频率特性呈低通性质，幅频穿越频率一般小于10 Hz，实测广域信号的传输时滞在0.1 s以内，对于0.1 s的时滞，为使在频带0～5 Hz范围内近似逼近，Pade近似阶数必须大于或等于2；而要保证在频带0～10 Hz范围内近似逼近，Pade近似阶数必须大于或等于3，因此在电力系统中可以采用3阶Pade近似逼近时滞[18]。

当选择第i台机组的速度差信号Δωi为广域反馈信号时，设X3=[x1，x2，…，xk]T为Pade近似表达状态变量，可得基于Pade近似的时滞环节状态空间表达式：

(7)

输出方程为：

(8)

前面分别推导了时滞环节、广域控制器和开环电力系统的线性化模型。由图1可见，对系统线性后参考输入为零，所以U1(t)=Y2(t)，联立式(2)至式(8)，可推导得到闭环电力系统线性化模型为：

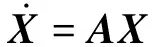
(9)

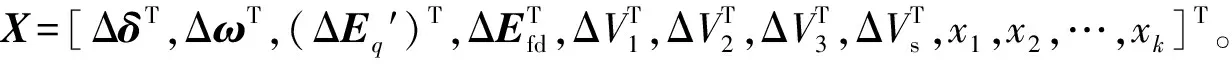
针对矩阵A研究时滞变化时对电力系统广域反馈背景下的区间振荡模态、局部振荡模态和时滞相关模态影响规律。电力系统低频振荡为发电机组间功率动态振荡，通过电气联系传递振荡能量，故称为机电振荡，包含区间振荡模态和局部振荡模态。区间振荡模态是指互联系统区域之间发电机转子间的相对摇摆，振荡频率在0.2～0.5 Hz之间；局部振荡模态指互联系统区域内部发电机转子间的相对摇摆，振荡频率在1～2.5 Hz之间，机电振荡模态和发电机转速有关；时滞相关模态是由于广域控制回路带来的控制模态，参与向量模值最大的分量与Pade近似状态变量有关，时滞对该控制模态影响显著。

2 时滞环节对电力系统区间振荡的影响分析及其实现

研究表明，利用PMU可以获取转子角和转子角速度等远方全局反馈信息，利用这些全局信息可形成广域反馈控制回路，这样可以提高系统阻尼，较好地抑制区间振荡模态，克服本地阻尼反馈对于区间振荡模态控制效果不甚理想的缺点。

本文采用留数矩阵法选择PSS安装位置及反馈信号。对式(2)代表的开环电力系统进行特征值计算，用λi表示第i个系统特征值，vi和ui分别为相应特征值对应的右、左特征向量，则传递函数矩阵可用留数矩阵表示：

(10)

(11)

式中：B和C分别为系统输入和输出矩阵；上标H表示共轭转置；Ri为特征值λi的留数矩阵。

Ri的第k行第l列元素为:

(12)

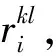
(13)

当广域PSS控制器的输入信号被延时τ时，包含时滞环节的广域PSS控制器变为：

(14)

因此，计及广域信号时延的广域PSS控制器构成的反馈控制对第i个模态的影响可以表示为：

(15)

设第i个机电模态为λi=σ+jω，则时滞环节带来的滞后相位φ和增益γ为：

(16)

由式(16)可以看出，时滞环节的相位是随时滞周期变化的，为机电模态λi带来周期变化的附加转矩，而其带来的附加增益随时滞呈指数规律变化，时滞环节的相位和幅值增益特性使机电模态的时滞变化轨迹呈旋转变化，后面仿真将验证这个结论。

下面事先指定PSS参数T2,T4,T5,T6，应用进化算法对PSS的其他参数Ks,T1,T3进行优化，以使具有最小阻尼比的机电振荡模态最大化。在此基础上，在控制回路引进时滞，从而研究时滞大小对电力系统区间振荡模态的影响规律。

时滞大小对电力系统区间振荡模态的影响规律的研究流程如下：①建立开环电力系统线性化模型，基于留数矩阵法选择广域反馈控制回路，建立广域闭环电力系统线性化模型；②利用智能进化算法对PSS的参数进行优化，以使具有最小阻尼比的机电振荡模态最大化；③引进广域信号通信时延，建立广域闭环电力系统线性化模型，利用稀疏特征值方法[19]，计算闭环电力系统的部分特征值，进而研究不同时滞对区间振荡模态、局部振荡模态和时滞相关模态的影响规律。

3 算例仿真

本文利用两区域四机系统和New England系统对所提方法进行仿真验证。系统参数分别见文献[2]和文献[20]。

3.1 两区域四机系统时滞影响规律分析

本文首先对两区域四机系统进行算例分析。采用留数矩阵法选择PSS安装位置为4号机组，反馈信号取自2号机组转速信号，建立无时滞电力系统广域反馈控制模型。本文PSS采用4阶模型，对PSS参数T2,T4,T5,T6指定为0.07，0.07，5，0.02，利用智能算法对Ks,T1,T3优化以使具有最小阻尼比的机电振荡模态最大化，区间模态和局部模态优化结果为-0.106±j3.347，-0.411±j7.00，-0.392±j6.709，系统稳定并且具有一定的阻尼比；在此基础上，采用上述参数构成计及时滞环节的广域反馈模型，研究时滞对电力系统区间振荡模态、局部振荡模态和时滞相关模态的影响规律。

当时滞环节采用3阶Pade近似模型，传输时滞在0～2 s之间变化时，研究时滞大小对区间振荡模态、局部振荡模态和时滞相关模态的影响规律，仿真结果如图2所示。由图2可以看出，即使对于0.02 s这样小的时滞，区间振荡模态具有0.000 17的正实部，从而使该模态动态响应特性变差，这说明时滞环节在该时滞情况下所提供的阻尼是负阻尼。随着时滞的变化，区间振荡模态的时滞变化轨迹按顺时针旋转变化，这是由于时滞环节具有周期相位特性和指数幅值增益特性，在励磁控制系统引入计及时滞环节的广域控制回路后，为区间振荡模态提供了周期变化的附加阻尼转矩，使该模态时滞变化轨迹旋转变化并部分越过虚轴，从而使该模态的阻尼比变负；对于两个局部振荡模态，时滞环节所带来的阻尼转矩使变化轨迹也呈顺时针变化，但时滞对局部振荡模态影响相对较小，依然具有负实部并且具有较大的阻尼比，从而没有影响系统的稳定性。另外，由于局部振荡模态比区间振荡模态的振荡频率高，这导致局部振荡模态旋转速度快；对于时滞相关模态，随着传输时滞的增加，实部从-0.725逐渐增大到0.060，其虚部由1.376下降到0.8，从而使时滞相关模态变化轨迹整体上向实轴正方向变化。可以看出，时滞相关模态实部变化范围比上述机电振荡模态的实部范围大很多，这表明时滞对时滞相关模态有显著的参与度，从而影响系统的稳定性。

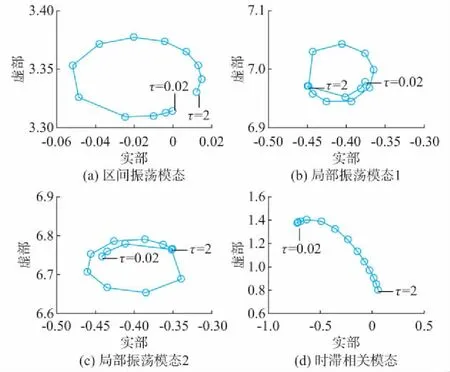
图2 3阶Pade近似的两区域四机系统时滞影响Fig.2 Time delay effect of third-order Pade approximation for two-area four-machine system

为验证Pade近似时滞模型阶数对各个模态计算结果的影响，其他仿真条件不变，采用10阶Pade近似时滞模型和牛顿精确特征值计算方法进一步验证上述的时滞影响规律。由图3可以看出，当采用10阶Pade近似时滞模型时，所有机电振荡模态的时滞变化轨迹依然有和上述3阶Pade近似时滞模型一样的变化趋势，但Pade近似时滞模型阶数对机电振荡模态旋转变化的速度有一定的影响。当时滞比较小时(小于1.0 s)，阶数对机电振荡模态基本没有影响；当时滞比较大时，采用高阶近似模型对机电振荡模态有一定的影响，加快时滞变化轨迹的旋转速度。这是因为Pade近似方法所产生的滞后相位小于实际时滞环节产生的滞后相位，而高阶近似模型逼近了实际时滞环节，从而加快了机电振荡模态周期变化速度，更加准确地刻画了时滞环节对机电振荡模态的影响规律。但时滞Pade近似阶数对于时滞相关模态变化趋势基本没有影响。

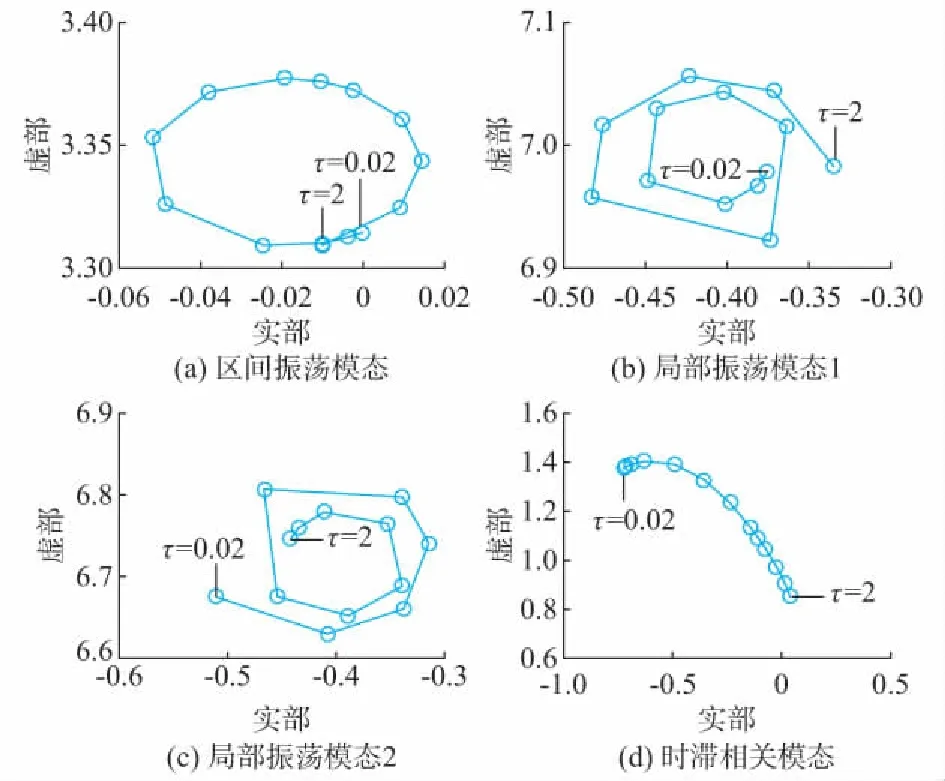
图3 10阶Pade近似的两区域四机系统时滞影响Fig.3 Time delay effect of tenth-order Pade approximation for two-area four-machine system

当采用Pade方法计算得到时滞0～2 s之间的系统区间振荡模态近似值后，进而以此作为牛顿法的初值计算得到相应的精确值。通过对比发现，在保留小数点后4位有效数字的情况下，所有模态的时滞变化轨迹和采用10阶Pade近似时滞模型计算的轨迹完全吻合，这进一步证明了Pade近似时滞模型阶数对上述各个模态时滞影响规律。

3.2 New England系统时滞影响规律分析

由于篇幅限制，New England系统时滞影响规律分析详见附录A。

4 结语

1)对于考虑时滞环节的广域反馈电力系统，时滞环节带来的附加周期相位特性和幅值特性使区间模态的时滞变化轨迹呈旋转变化趋势并可能越过虚轴进入右半平面，从而影响系统的稳定性。

2)时滞环节只对广域反馈安装机组参与的局部模态有一定的影响，使其时滞变化轨迹只在左半平面小范围旋转变化，不会影响系统的稳定性，但对其他局部模态基本没有影响。

3)对于时滞相关模态，其变化轨迹整体上向实轴正方向变化，时滞相关模态实部有比较明显的变化范围，从而影响整个系统的稳定性。

4)当时滞比较大时，高阶Pade近似模型更加准确地刻画了时滞环节对机电振荡模态的影响规律。

但广域电力系统关键特征值时滞轨迹变化趋势和控制器设计还存在较为复杂的关系，需要进一步加以研究。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参考文献

[1] 周涛,陈中,殷大朋,等.基于阻尼转矩分析法的时滞丢包统一建模及其应用[J].电力系统自动化,2017,41(5):53-57.DOI:10.7500/AEPS20160531010.

ZHOU Tao, CHENG Zhong, YIN Dapeng, et al. Damping torque analysis based unified modeling of time delay and data loss and its application[J]. Automation of Electric Power Systems,2017, 41(5): 53-57. DOI: 10.7500/AEPS20160531010.

[2] KUNDUR P.电力系统稳定与控制[M].北京:中国电力出版社,2002:465-552.

[3] LI Yong, LIU Fang, CAO Yijia. Sequential design and global optimization of local power system stabilizer and wide-area HVDC stabilizing controller[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(2): 292-299.

[4] 李宁,孙永辉,卫志农,等.基于Wirtinger不等式的电力系统延时依赖稳定判据[J].电力系统自动化,2017,41(2):108-113.DOI:10.7500/AEPS20160418002.

LI Ning, SUN Yonghui, WEI Zhinong, et al. Delay-dependent stability criteria for power system with Wirtinger-based integral inequality[J]. Automation of Electric Power Systems, 2017, 41(2): 108-113. DOI: 10.7500/AEPS20160418002.

[5] 马燕峰,周一辰,赵书强,等.考虑交互作用的多阻尼控制器独立设计的控制环选择[J].电工技术学报,2016,31(4):136-146.

MA Yanfeng,ZHOU Yichen,ZHAO Shuqiang,et al.Control loops selection for independent design of multiple damping controllers with interactions considered[J]. Transactions of China Electrotechnical Society, 2016, 31(4): 136-146.

[6] 王蕾,董朝宇,贾宏杰,等.电力系统时滞稳定判据保守性差异量化评估方法[J].电力系统自动化,2017,41(10):22-28.DOI:10.7500/AEPS20160721012.

WANG Lei, DONG Chaoyu, JIA Hongjie, et al. Diversity-based quantitative evaluation method of conservative property of time-delay stability criteria for power systems[J]. Automation of Electric Power Systems, 2017, 41(10): 22-28. DOI: 10.7500/AEPS20160721012.

[7] ZIRAS C,VRETTOS E,YOU S. Controllability and stability of primary frequency control from thermostatic loads with delays[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(1): 43-54.

[8] 张放,程林,黎雄,等.广域闭环控制系统时延的测量及建模:(一)通信时延及操作时延[J].中国电机工程学报,2015,35(22):5768-5777.

ZHANG Fang, CHENG Lin, LI Xiong, et al. Delay measurement and modeling in a wide-area closed-loop control system: Part Ⅰ communication delay and operational delay[J]. Proceedings of the CSEE, 2015, 35(22): 5768-5777.

[9] 王德进.时滞系统低阶控制器设计:参数空间法[M].北京:科学出版社,2013:28-45.

[10] 余晓丹,贾宏杰,王成山.时滞电力系统全特征谱追踪算法及其应用[J].电力系统自动化,2012,36(24):10-14.

YU Xiaodan, JIA Hongjie, WANG Chengshan. An eigenvalue spectrum tracing algorithm and its application in time delayed power systems[J]. Automation of Electric Power Systems, 2012, 36(24): 10-14.

[11] 王成山,石颉.考虑时间延迟影响的电力系统稳定器设计[J].中国电机工程学报,2007,27(10):1-6.

WANG Chengshan, SHI Jie. PSS designing with consideration of time delay impact[J]. Proceedings of the CSEE, 2007, 27(10): 1-6.

[12] 叶华,霍健,刘玉田.基于Pade近似的时滞电力系统特征值计算方法[J].电力系统自动化,2013,37(7):25-30.

YE Hua, HUO Jian, LIU Yutian. A method for computing eigenvalue of time-delayed power systems based on Pade approximation[J]. Automation of Electric Power Systems, 2013, 37(7): 25-30.

[13] 袁野,程林,孙元章.考虑时延影响的互联电网区间阻尼控制[J].电力系统自动化,2007,31(8):12-16.

YUAN Ye, CHENG Lin, SUN Yuanzhang. Inter-area damping control of interconnected power systems considering the time delay of feedback signal[J]. Automation of Electric Power Systems, 2007, 31(8): 12-16.

[14] 刘梅招,辛焕海,甘德强.计及广域阻尼控制的PSS均匀通信时滞极限计算[J].电力系统自动化,2007,31(22):16-20.

LIU Meizhao, XIN Huanhai, GAN Deqiang. Computing delay margin of PSS with commensurate communication delay considering wide-area damping control[J]. Automation of Electric Power Systems, 2007, 31(22): 16-20.

[15] 董存,余晓丹,贾宏杰.一种电力系统时滞稳定裕度的简便求解方法[J].电力系统自动化,2008,32(1):6-10.

DONG Cun, YU Xiaodan, JIA Hongjie. A simple method to determine power system delay margin[J]. Automation of Electric Power Systems, 2008, 32(1): 6-10.

[16] 贾宏杰,尚蕊,张宝贵.电力系统时滞稳定裕度求解方法[J].电力系统自动化,2007,31(2):5-11.

JIA Hongjie, SHANG Rui, ZHANG Baogui. Computation of delay stability margin of electric power systems[J]. Automation of Electric Power Systems, 2007, 31(2): 5-11.

[17] 刘兆燕,戚军,苗轶群,等.单时滞电力系统时滞稳定裕度的简便求解方法[J].电力系统自动化,2008,32(18):8-13.

LIU Zhaoyan, QI Jun, MIAO Yiqun, et al. A simple method to compute delay margin of power system with single delay[J]. Automation of Electric Power Systems, 2008, 32(18): 8-13.

[18] 陆超,张俊勃,韩英铎.电力系统广域动态稳定辨识与控制[M].北京:科学出版社,2015:281-309.

[19] 杜正春,刘伟,方万良,等.小干扰稳定性分析中按阻尼比递增的关键特征值子集计算[J].电网技术,2006,30(3):7-12.

DU Zhengchun, LIU Wei, FANG Wanliang, et al. Calculation of critical eigenvalues with increasing damping ratios in small signal stability analysis[J]. Power System Technology, 2006, 30(3): 7-12.

[20] PBD A, LCZ J. Pole placement method using the system matrix transfer function and sparsity[J]. Electrical Power and Energy Systems, 2001, 23(3): 173-178.