用于迭代法潮流计算的改进Jacobi预处理方法

唐 灿, 董树锋, 任雪桂, 尹 璐, 鞠 力

(1. 浙江大学电气工程学院, 浙江省杭州市 310027; 2. 北京电力经济技术研究院, 北京市 100055)

0 引言

牛顿—拉夫逊法是常见的电力系统交流潮流计算方法之一。这一方法需要多次迭代运算,每一次迭代过程中都需要求解线性方程组。当方程组的规模较大时,求解方程组非常耗时,潮流计算的效率受到较大影响。

直接法[1]和迭代法[2-5]是求解线性方程组的两类方法。其中直接法主要利用矩阵分解技术求解,例如LU分解法等,虽然直接法能通过有限步骤算出精确解,但计算复杂度较高,且计算过程不利于并行处理,不适合求解大规模的线性方程组。相较于直接法,迭代法易于并行计算,在求解大规模线性方程组时具有明显的优势[6]。随着图形处理器(GPU)的飞速发展,中央处理器(CPU)与GPU异构协同的计算体系使得串行计算与并行计算协调运作,显著提高了计算能力[7-10],因此可以考虑利用这一计算体系实现迭代法的潮流计算方法。

但是,迭代法也有不足,相比于直接法具有不稳定性。迭代法的收敛速度与系数矩阵的条件数和谱分布紧密相关,当谱分布较为分散时,迭代法的收敛速度明显降低甚至会发生不收敛的情况。为保证迭代法线性方程组求解时的稳定性,提高求解速度,需要将原方程组转换为等价的、易于求解的线性方程组。针对这一问题,通常采用预处理技术,即通过对系数矩阵进行预处理,改善系数矩阵的谱分布,使其分布地更为集中,从而提高迭代法的稳定性及收敛速度。

在进行预处理时,往往存在预处理效果与预处理时间的矛盾,要想取得较好的预处理效果往往需要耗费更多时间。本文提出了一种适合于超大规模电力系统潮流计算中Jacobi矩阵的预处理方法,这一方法基于适于并行的Jacobi预处理法,并充分利用Jacobi矩阵自身特点对传统预处理方法进行改进。并行求解其预处理子,不仅拥有高效的求解速度,同时拥有超过其他轻量级预处理子的效果。经算例测试,所提的预处理方法能有效集中谱分布,改善条件数,提高方程组求解速度。

1 Krylov子空间迭代法的预处理

Krylov子空间迭代法是一种高效求解大型稀疏线性方程组的有效方法[11-13]。利用Krylov子空间迭代法求解线性方程组时,其收敛速度取决于其谱分布[14-15]。谱分布越集中,其收敛速度越快。

为了提高收敛速度,可以对系数矩阵进行预处理。一般来说,预处理包括以下三种形式。

M-1Ax=M-1b

(1)

(2)

(3)

式中:A为线性方程组的系数矩阵;b为常数项;x为待求向量;y为中间向量;M为预处理子,M1和M2由预处理子分解得到。

式(1)中分别对Ax和b左乘M-1,然后求解新的线性方程组,其结果与原方程的解相等；式(2)中对A右乘M-1y,可看作是AM-1(Mx)=b,求解得到Mx,对结果左乘M-1即可得到与原方程相同的解；式(3)是式(1)和式(2)的结合,同样可以得到与原方程同样的解。对于本文所选取的预处理子M,既可以使用式(1)与式(2)进行预处理,也可以将M分解为M1M2,并采用式(3)进行预处理。

预处理子的选择除了应当使得处理后的方程组更易求解外,也要注意保证原系数矩阵的稀疏性,尽可能控制非零元注入的数量。此外,所选的预处理子的构造过程的计算开销应尽可能低。

常用的预处理方法包括不完全分解预处理[16-21]、近似逆预处理[22-23]和多项式预处理[24-26]等。不完全分解方法的实现过程难以并行,不适用于系数矩阵规模较大的情形;近似逆预处理容易破坏稀疏矩阵逆矩阵的稀疏性;多项式预处理方法虽具有自然可并行性,但是这一方法得到的预处理子的预处理效果较差。

在实际计算中,Jacobi预处理法是较为常用的预处理方法。Jacobi预处理法直接取矩阵的对角元作为预处理子,其主要优势在于其预处理的速度非常快,缺点是仅适用于对角元占主导的矩阵。电力系统的潮流计算的Jacobi矩阵是一种类对角元占主导的矩阵,采用Jacobi预处理法能够在一定程度上提高潮流计算的速度。但是,潮流计算的Jacobi矩阵并非真正意义上的对角元占主导的矩阵,为了进一步提高预处理的效果,本文基于适于并行的Jacobi预处理,充分利用Jacobi矩阵自身特点,设计了新的预处理子。

2 改进Jacobi预处理方法

在潮流计算中,极坐标表示的节点功率方程为[27]:

(4)

式中:Pi和Qi分别为节点i注入的有功功率和无功功率；Ui和Uj分别为节点i和节点j的电压幅值；δij为节点i和j的相角差;Gij和Bij分别为节点i和节点j间的互电导与互电纳。

由此可得到描述电力系统的非线性方程。根据牛顿—拉夫逊算法,线性化潮流方程可以得到修正方程组[27]为:

(5)

式中:ΔP和ΔQ分别为节点实际注入功率与迭代过程中值的差额;H,N,J,L分别为迭代过程中Jacobi矩阵的4个子矩阵;ΔV和Δθ分别为相邻两次迭代中电压幅值与相角之间的差值。其中,H为n-1阶方阵；N为(n-1)×(n-1-r)阶矩阵;J为(n-1-r)×(n-1)阶矩阵；L为n-1-r阶方阵。H,N,J,L这4个子矩阵都可以通过补充若干全零元素组成的行和列得到n阶方阵。

若系统的节点数为n,其中PV节点数为r，则修正方程组的系数矩阵为n-r-1阶的结构对称矩阵。

Jacobi矩阵中各元素的计算表达式为[27]:

(6)

(7)

(8)

(9)

式中:Hii=∂ΔPi/∂θi,Hij=∂ΔPi/∂θj,Nii=∂ΔPi/∂Vi,Nij=∂ΔPi/∂Vj,Jii=∂ΔQi/∂θi,Jij=∂ΔQi/∂θj,Lii=∂ΔQi/∂Vi,Lij=∂ΔQi/∂Vj；i和j分别为系统的节点编号,而不表示元素在矩阵中的行列号。

由式(6)至式(9)可知,Hii,Nii,Jii,Lii分别在H,N,J,L这4个子矩阵中占优。因此,利用这些元素,可以构造预处理子。即

(10)

取H,N,J,L中占主导的元素,分别得到Aij,Bij,Cij,Dij并满足式(11)至式(14)。即

(11)

(12)

(13)

(14)

预处理子M具有以下性质。

1)M为高度稀疏矩阵,其子矩阵A,B,C,D每行的非零元和每列的非零元数量均不超过1个。同时,A和D为(n-1)×(n-1)阶对角矩阵,BT和C为(n-1-r)×(n-1)阶矩阵,且非零元的位置相同。

2)对M进行求逆无非零元注入,证明过程如下。

令

(15)

则

(16)

当H,L,H-NL-1J,L-JH-1N都可逆时, 解得:

(17)

以M-1的子矩阵X1为例。由于D为n-1阶对角矩阵,而BT和C为(n-1-r)×(n-1)阶矩阵,且具有相同的非零元素分布,故BD-1C为对角矩阵。则X1=(A-BD-1C)-1与A同为(n-1)×(n-1)阶对角矩阵。同理,X2,X3,X4分别与子矩阵B,C,D具有相同的非零元位置。故M-1不引入任何非零元注入。

在计算方面,由于A,D,A-BD-1C，D-CA-1B均为对角矩阵,B与C的非零元位置互为转置且每行至多只有一个非零元。可以采用特殊的方法快速求解:①稀疏矩阵求逆时,只需对每个对角元分别求逆;②稀疏矩阵相乘时,将其中一个矩阵转置,转置后矩阵的非零元与另一个矩阵中对应的非零元分别相乘即可。这一过程具有自然可并行性,可以利用GPU通用计算加速实现。

3 算例分析

3.1 Jacobi矩阵谱分布的改善效果分析

为验证本文所提出的预处理方法能够有效改善系数矩阵的谱分布,选取IEEE标准系统和PSS/E软件自带的BENCH算例测试,对比不同预处理方法下在预处理前后的特征值分布。由表1可知,利用本文方法进行预处理后,各算例谱分布集中于0～2之间,相比较于优化前有明显改善。Jacobi预处理也能改善矩阵谱分布,但效果不如本方法。

由图1可知,IEEE 39,IEEE 118,IEEE 300算例和BENCH算例经预处理后,特征值分布变得集中。相比于Jacobi预处理,本文所提方法效果更为显著,尤其是虚轴方向上的特征值分布,处理后的最大特征值的虚部约为0。

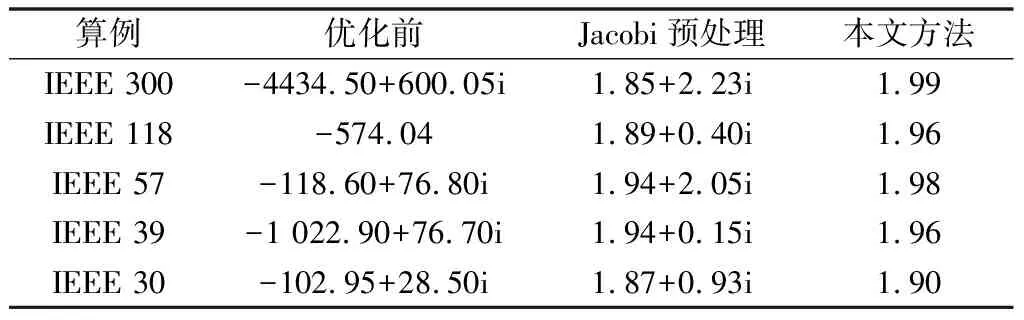
表1 预处理前后Jacobi矩阵最大特征值Table 1 Maximum eigenvalue of Jacobi matrix before and after pre-treatment

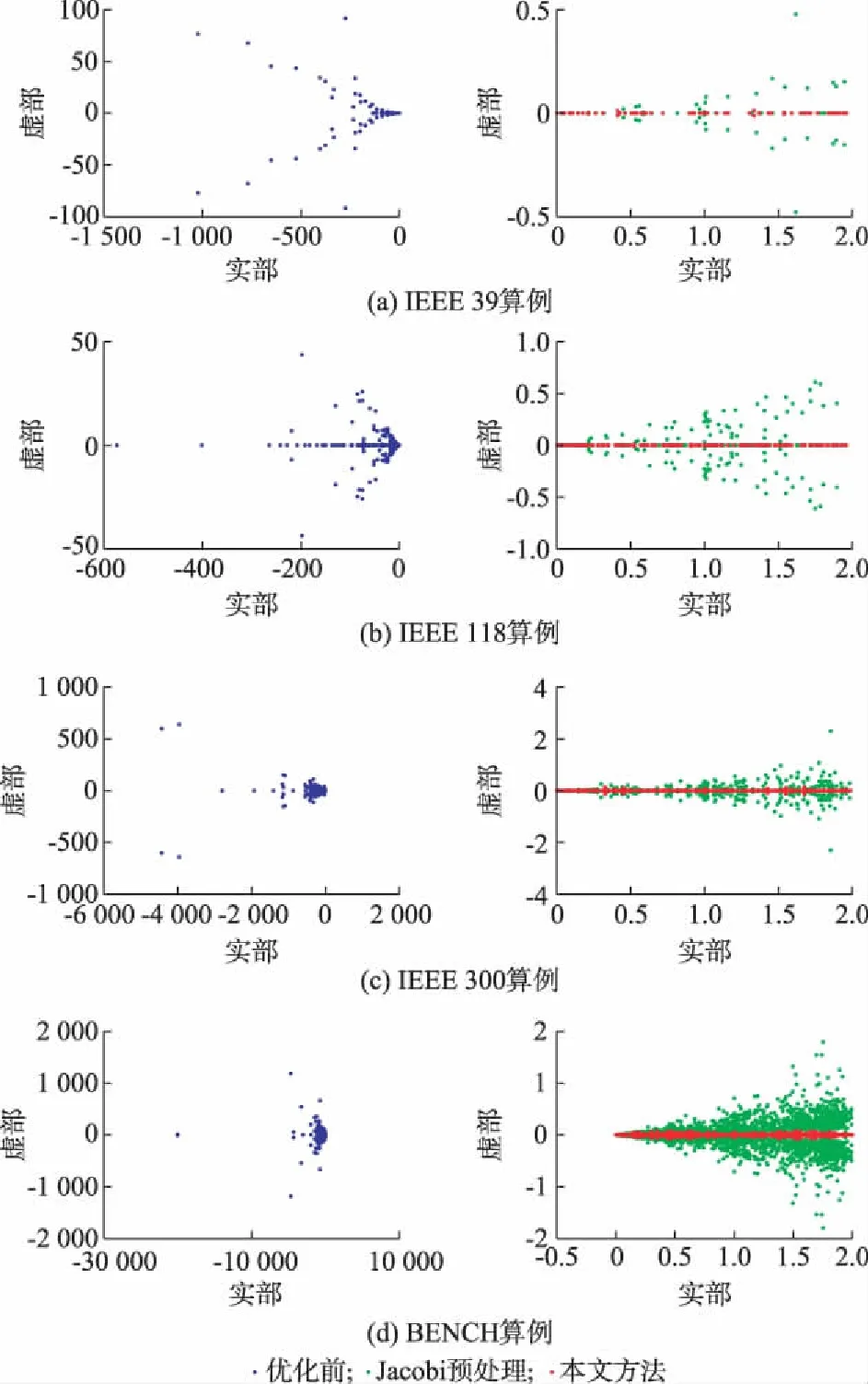
图1 预处理前后Jacobi矩阵特征值分布Fig.1 Distribution of eigenvalue of Jacobi matrix before and after pre-treatment

3.2 M-1与A-1的近似程度

为了比较采用上述方法求取预处理子时A-1和M-1的近似程度,选取‖Err‖F/n2,‖Err‖1/n,max(Err)作为参考标准。其中Err为误差矩阵,等于A-1和M-1差值的绝对值；‖Err‖F为Err的Frobenius范数,‖Err‖1为Err的1-范数。‖Err‖F/n2为A-1与M-1每个元素的平均偏差,‖Err‖1/n为A-1与M-1每行平均值的最大偏差,max(Err)为A-1与M-1每个元素之间的最大差值。表2统计了用不同算例时，A-1和M-1的近似程度。

表2 预处理后A-1和M-1的近似程度Table 2 Degree of approximation of A-1 and M-1 after pre-treatment

从表2的结果可以看出,采用该方法进行预处理后,M-1和A-1在数值上十分接近；从‖Err‖F/n2的值可以看出，预处理后每个元素的平均偏差小于0.001；从‖Err‖1/n可以看出，预处理后每行平均值最大偏差小于0.1；从max(Err)可以看出,预处理后对应元素之间差额小于1.96。由此可见,该预处理方法拥有较好的效果。

3.3 预处理方法的有效性验证

为了进一步验证本文提出的预处理方法的有效性,选取多个算例测试预处理方法对迭代法迭代次数的影响。其中,IEEE 8971算例由30个完全相同的IEEE 300系统拼接平衡节点得到。迭代法采用了稳定化的双共轭梯度(BiCGSTAB)法、双共轭梯度(BiCG)法、共轭梯度平方(CGS)法、最小残差法共准(QMR)这4种常用的Krylov子空间迭代法。表3 对比了无预处理、Jacobi预处理和本文预处理3种情形下求解线性方程组所需的平均迭代次数。其中,迭代法的计算精度取0.001。

从表3可以看出,将本文的预处理方法应用于不同的迭代法进行线性方程组求解均可以大幅减少迭代次数,从而减少计算时间。当系统规模较大时,如BENCH迭代法,预处理效果更加明显,能够减少90%以上的迭代次数。相比较于常见的Jacobi预处理方法,具有显著的优势。

采用预处理时能够减少潮流计算中求解线性方程组时的迭代次数与迭代时间,但预处理过程本身需要占据时间。为了权衡预处理方法本身计算的耗时和提升迭代收敛性带来的计算效率提升之间的关系,同时考虑到ILU0预处理子也是商业软件常用的预处理方法,表4统计了本文方法、Jacobi预处理方法和 ILU0预处理方法应用于计算潮流时所需要的预处理时间及总时间。计算采用的CPU型号为Intel i7-4710MQ,主频为2.5 GHz,内存为16 GB,线性方程组求解部分采用CULA计算包中的BiCGSTAB方法求解,采用的显卡为NVDIA GTX860M。其中IEEE 8971算例和IEEE 1496算例由多个IEEE 300算例系统拼接平衡节点得到。

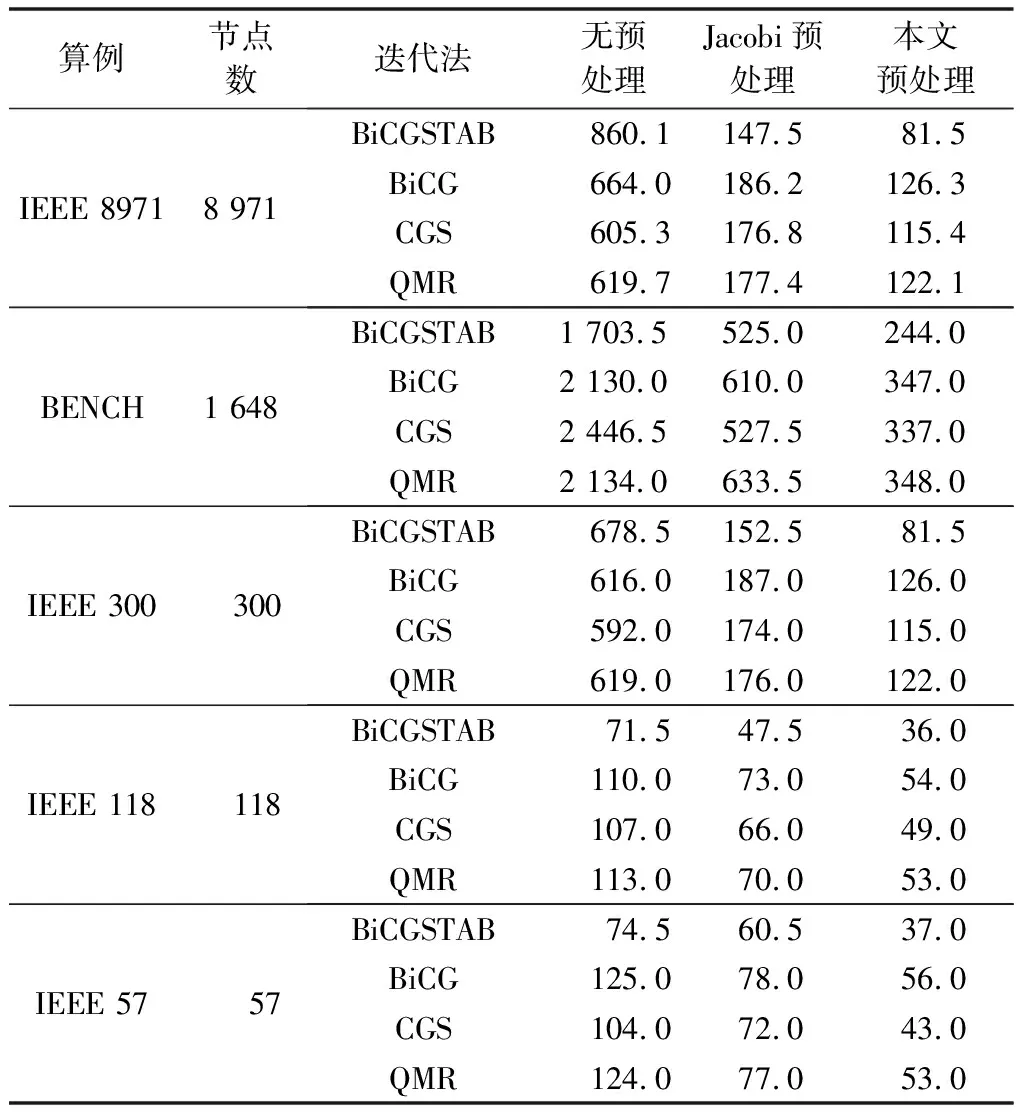
表3 预处理与无预处理时潮流计算中求解线性方程组时的迭代次数Table 3 Iterations of solving linear equations when doing power flow calculation with and without pre-treatment

由表4可以看出,采用本文的预处理方法可以大大减少线性方程组的求解时间,并增加求解的稳定性。在以上算例中,Jacobi预处理子耗时均小于1 ms,可忽略不计；ILU0预处理子耗时相对较大,占总耗时的6.6%～16%；本文方法耗时介于二者之间,小于总耗时的3%。从总耗时来看本方法远好于Jacobi预处理子,与ILU0预处理子耗时接近。

3.4 算法总体效率测试

本文的预处理方法能够有效地加速潮流计算,本文选取了CULA软件包进行对比测试。在采用CULA软件包进行潮流计算线性方程组求解时,很多求解器与预处理子的组合都不能有效地收敛,其中较为稳定的组合是BiCGSTAB求解器与ILU0预处理子或Jacobi预处理子,但是由于ILU0预处理子速度更快,于是CULA的数据采用了BiCGSTAB+ILU0进行计算。具体数据见附录A表A1。本文提出的预处理方法应用于潮流计算,总体性能优于CULA软件包,可满足在线计算要求。

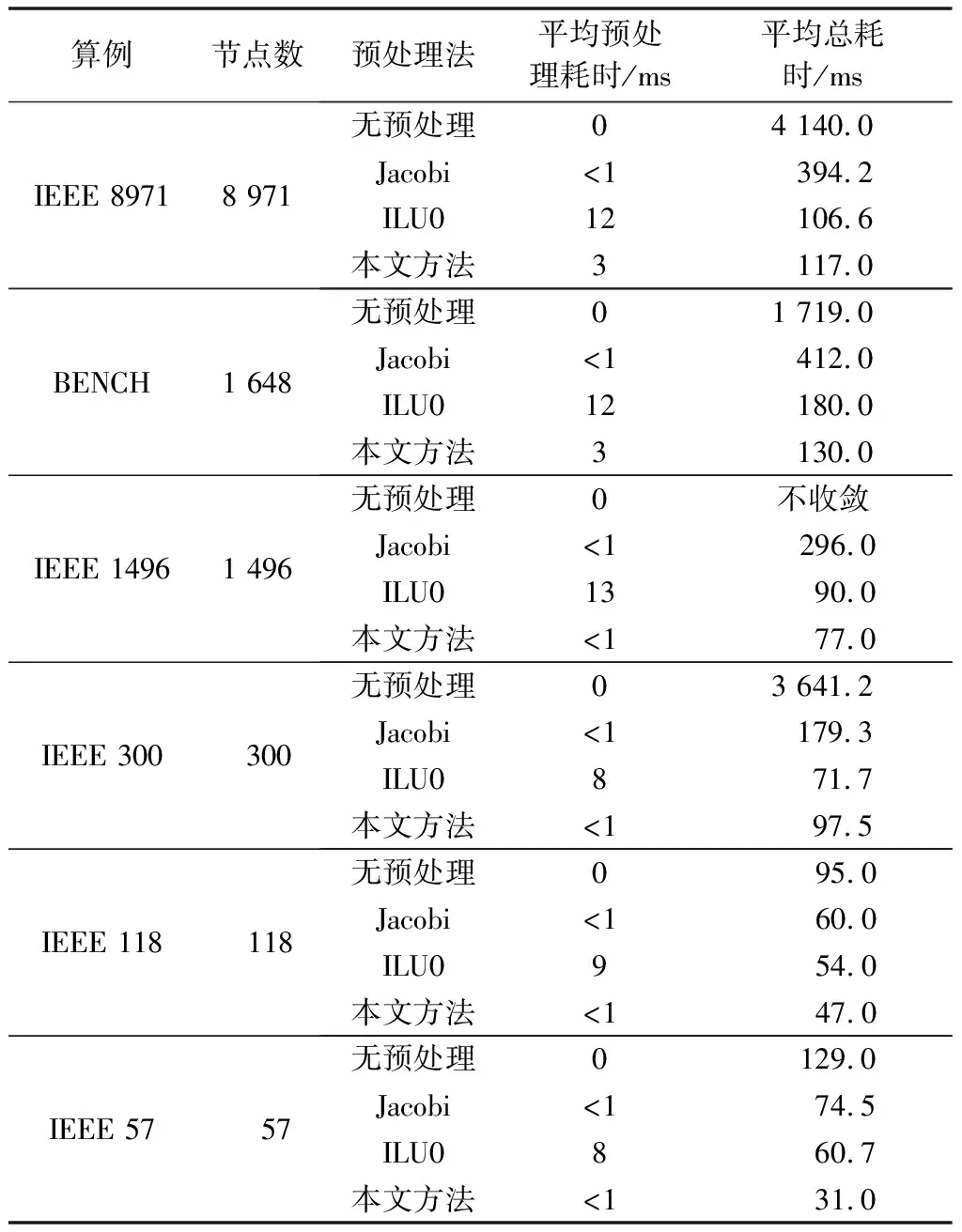
表4 不同预处理方法下进行潮流计算时求解线性方程组耗时Table 4 Time of solving linear equations when doing power flow calculation with different pre-treatment methods

4 结语

本文提出了一种用于迭代法潮流计算的改进Jacobi预处理方法。经算例测试表明,所提的预处理方法构建预处理子速度快,同时能够有效地集中特征值分布、改善条件数、显著减少迭代次数,满足大规模电网在线潮流计算的需求,具有工程应用的潜力和价值。

由于本方法基于牛顿—拉夫逊法潮流计算中的Jacobi矩阵的特性来构建预处理子,尚无法直接应用于其他的电力系统计算,在今后的研究中,应当考虑在其他领域的应用。另一方面,改进Jacobi预处理法预处理后的系数矩阵仍有优化空间,可考虑多个预处理子结合的多步预处理,进一步加速Krylov子空间法的收敛速度。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参考文献

[1] 徐晓飞,曹祥玉,姚旭,等.一种基于Doolittle LU分解的线性方程组并行求解方法[J].电子与信息学报,2010,32(8):2019-2022.

XU Xiaofei, CAO Xiangyu, YAO Xu, et al. Parallel solving method of linear equations based on Doolittle LU decomposition[J]. Journal of Electronics & Information Technology, 2010, 32(8): 2019-2022.

[2] HOU G, WANG L. A generalized iterative method and comparison results using projection techniques for solving linear systems[J]. Applied Mathematics and Computation, 2009, 215(2): 806-817.

[3] AHAMED A C, MAGOULES F. Iterative methods for sparse linear systems on graphics processing unit[C]// 2012 IEEE 14th International Conference on High Performance Computing and Communications & 2012 IEEE 9th International Conference on Embedded Software and Systems, June 25-27, 2012, Liverpool, United Kingdom: 836-842.

[4] LEON F D, SERNLYEN A. Iterative solvers in the Newton power flow problem: preconditioners, inexact solutions and partial Jacobi updates[J]. IEEE Proceedings: Generation, Transmission and Distribution, 2002, 149(4): 479-484.

[5] KULKARNI A Y, PAI M A, SAUER P W. Iterative solver techniques in fast dynamic calculations of power systems[J]. International Journal of Electrical Power & Energy Systems, 2001, 23(3): 237-244.

[6] 蔡大用,陈玉荣.用不完全LU分解预处理的不精确潮流计算方法[J].电力系统自动化,2002,26(8):11-14.

CAI Dayong, CHEN Yurong. Solving power flow equations with inexact newton methods preconditioned by incomplete LU factorization with partially fill-in[J]. Automation of Electric Power Systems, 2002, 26(8): 11-14.

[7] 王海峰,陈庆奎.图形处理器通用计算关键技术研究综述[J].计算机学报,2013,36(4):757-772.

WANG Haifeng, CHEN Qingkui. General purpose computing of graphics processing unit: a survey[J]. Chinese Journal of Computers, 2013, 36(4): 757-772.

[8] 郭春辉.基于GPU的电力系统并行计算的研究[D].济南:山东大学,2013.

[9] 张逸飞,严正,赵文恺,等.基于GPU的分块约化算法在小干扰稳定分析中的应用[J].电力系统自动化,2015,39(22):90-97.DOI:10.7500/AEPS20150126012.

ZHANG Yifei, YAN Zheng, ZHAO Wenkai, et al. Application of block reduction algorithm in power system small-signal stability analysis[J]. Automation of Electric Power Systems, 2015, 39(22): 90-97. DOI: 10.7500/AEPS20150126012.

[10] 周挺辉,赵文恺,严正,等.基于图形处理器的电力系统稀疏线性方程组求解方法[J].电力系统自动化,2015,39(2):74-80.DOI:10.7500/AEPS20131119005.

ZHOU Tinghui, ZHAO Wenkai, YAN Zheng, et al. A method for solving sparse linear equations power systems based on GPU[J]. Automation of Electric Power Systems, 2015, 39(2): 74-80. DOI: 10.7500/AEPS20131119005.

[11] ZHANG J. Preconditioned Krylov subspace methods for solving nonsymmetric matrices from CFD applications[J]. Computer Methods in Applied Mechanics and Engineering, 1998, 189(3): 825-840.

[12] SAAD Y, VORST H. Iterative solution of linear systems in the 20th century[J]. Journal of Computational and Applied Mathematics, 2000, 123(1): 1-33.

[13] 陈颖,沈沉,梅生伟,等.基于改进Jacobi-Free Newton-GMRES(m)的电力系统分布式潮流计算[J].电力系统自动化,2006,30(9):5-8.

CHEN Ying, SHEN Cheng, MEI Shengwei, et al. Distributed power flow calculation based on an improved Jacobian-free Newton-GMRES(m) method[J]. Automation of Electric Power Systems, 2006, 30(9): 5-8.

[14] AXELSSON O, LINDSKOG G. On the eigenvalue distribution of a class of preconditioning methods[J]. Numerische Mathematik,1986, 48(5): 479-498.

[15] JIA Z. The convergence of Krylov subspace methods for large unsymmetric linear systems[J]. Acta Mathematica Sinica, New Series, 1998, 14(4): 507-518.

[16] ZHANG J. A grid-based multilevel incomplete LU factorization preconditioning technique for general sparse matrices[J]. Applied Mathematics and Computation, 2001, 43(4): 483-500.

[17] SAAD Y, ZHANG J. Enhanced multi-level block ILU preconditioning strategies for general sparse linear systems[J]. Journal of Computational and Applied Mathematics, 2001, 130(1): 99-118.

[18] WILLE S O, STAFF O, LOULA A. Block and full matrix ILU preconditioners for parallel finite element solvers[J]. Computer Methods in Applied Mechanics and Engineering, 2002, 191(13): 1381-1394.

[19] SHEN C, ZHANG J. Parallel two level block ILU preconditioning techniques for solving large sparse linear systems[J]. Parallel Computing, 2002, 28(10):1451-1475.

[20] LEE J, ZHANG J, LU C. Incomplete LU preconditioning for large scale dense complex linear systems from electromagnetic wave scattering problems[J]. Journal of Computational Physics, 2003, 185(1): 158-175.

[21] 柳建新,蒋鹏飞,童孝忠,等.不完全LU分解预处理的BICGSTAB算法在大地电磁二维正演模拟中的应用[J].中南大学学报(自然科学版),2009,40(2):484-491.

LIU Jianxin, JIANG Pengfei, TONG Xiaozhong, et al. Application of BICGSTAB algorithm with incomplete LU decomposition preconditioning to two-dimensional magnetotelluric forward modeling[J]. Journal of Central South University (Science and Technology), 2009, 40(2): 484-491.

[22] KAEBI A, KERAYECHIAN A, TOUTOUNIAN F. Approximate inverse preconditioner by computing approximate solution of Sylvester equation[J]. Applied Mathematics and Computation, 2005, 170(2): 1067-1076.

[23] ZHANG J. A sparse approximate inverse preconditioner for parallel preconditioning of general sparse matrices[J]. Applied Mathematics and Computation, 2002, 130(1): 63-85.

[24] NOTAY Y. Polynomial acceleration of iterative schemes associated with subproper splittings[J]. Journal of Computational and Applied Mathematics, 1988, 24(1): 153-167.

[25] CERDAN J, MAR N, MART N A. Polynomial preconditioners based on factorized sparse approximate inverses[J]. Applied Mathematics and Computation, 2002, 133(1): 171-186.

[26] ZHANG J, ZHANG L. Efficient CUDA polynomial preconditioned conjugate gradient solver for finite element computation of elasticity problems[J]. Mathematical Problems in Engineering, 2013(6): 1-12.

[27] 陈德扬,李亚楼,江涵,等.基于道路树分层的大电网潮流并行算法及其GPU优化实现[J].电力系统自动化,2014,38(22):63-69.DOI:10.7500/AEPS20131014009.

CHEN Deyang, LI Yalou, JIANG Han, et al. A parallel power flow algorithm for large-scale grid based on stratified path trees and its implementation on GPU[J]. Automation of Electric Power Systems, 2014, 38(22): 63-69. DOI: 10.7500/AEPS20131014009.