基于两组对称开口环结构的可开关双频段左手材料

张效雄， 杨荣草

(山西大学 物理电子工程学院， 山西 太原 030006)

0 引 言

左手材料是一种人工亚波长结构， 继Veselago对左手材料的理论预测[1]和Pendry等人对金属线-开口环结构的研究之后[2-4]， 人工合成的左手材料得到广泛发展， 左手材料能够表现出许多奇异的特性， 包括： 负折射效应[4]、 人工磁性[2]、 波长选择性吸收[5]、 完美透镜效应[6]等. 负介电常数和负磁导率是描述左手材料的两个本构参数， Smith等人实验证明负介电常数和负磁导率可通过电场作用在金属线阵列和磁场作用在开口环结构来实现， 当同一频段内同时出现负介电常数和负磁导率时， 金属线-开口环结构能够表现出左手特性[3]. 后续的研究者采用相似的方法设计出多频段的负折射材料， 例如Sarkhel等人提出了一种双频段小型化负介电常数材料[7]， 该结构的优点在于它的单元结构小， 可利用谐振耦合机制产生双频段， 但是其内部结构较复杂； 他们还提出了一种多频段负折射材料， 相比于传统的多频段负折射材料， 该结构没有采用相同结构不同尺寸的谐振器排列或嵌套的方式， 而是结合了电谐振器和混合型环状谐振器， 避免了谐振器之间的相互作用[8]； Faruque等人设计并分析了由两个C型结构组成的小型化多频段超材料[9]. 虽然以上结构在带宽和频率的选择性方面均有改善， 但是它们的研究范围局限于固定参数的无源媒质， 无法实现谐振频率的可调谐或者可开关， 这在一定程度上限制了左手材料的实际应用. 可调谐或者可开关的左手材料是当前的研究热点. 基于液晶、 变容二极管、 RF MEMS等可调谐元件， 研究者们设计出许多可调谐超材料， 将以上元件加载到谐振结构或介质当中， 通过外加光信号或电信号改变可调谐元件电压来控制其电磁响应. 例如G.Isi等人提出了基于向列型液晶的可调谐太赫兹超材料吸收器[10]； Kim等人设计了一种加载变容二极管的渔网型可调谐超材料吸收器[11]； Bensafieddine等人提出了一种可调谐微波传输线， 在单元结构的不同开口位置处加载RF MEMS开关， 通过改变其状态来控制不同位置处的磁谐振， 实现频率可调谐的微波传输线[12]. 磁谐振响应是实现左手通带的关键特性之一， 改变左手材料的磁谐振频率为实现可调谐左手材料提供了一个新途径.

目前， 为了能够将左手材料应用在具有复杂表面的特殊领域， 灵活多样的左手材料得到广泛发展. 随着技术的发展与进步， 新型聚合物由于具有灵活性及稳定性而被用来实现柔性左手材料[13,14]， 在众多聚合物当中， 聚酰亚胺层可与沉积在其上面的金属层之间很好地粘合， 除了具有良好的机械延展性和拉伸强度， 还具有较低的介电常数和低损耗等， 使其非常适合作为介质层.

本文采用聚酰亚胺聚合物作为介质层， 设计了一种基于两组对称开口环结构的可开关双频段左手材料， 能够通过改变对应环的开口状态来实现低频-高频响应的可开关特性， 并且分析了不同开口位置处开关状态对双频段特性的影响.

1 单元结构

本文提出的单元结构由两组对称的开口环、 3条金属线和介质基板组成， 如图 1～图 3 所示.

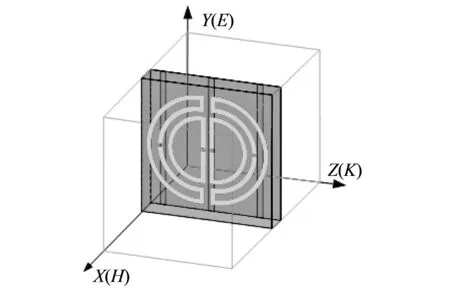
图 1 单元结构示意图Fig.1 Configuration of a unit cell

在微波频段， 为了实现可调谐左手材料， 把RF MEMS集成在单元结构中是一种重要手段[15,16]. 由于RF MEMS开关能够在截止状态表现出良好的绝缘性以及在导通状态时拥有较小的阻抗等优良性能， 在开口间隙处加载RF MEMS开关， 通过控制其状态来实现不同的电磁响应. 两组对称的开口环结构刻蚀在介质基板的一侧， 3条相同的金属线刻蚀在另一侧， 采用聚酰亚胺材料作为介质基板， 相对介电常数为=3.5， 厚度d=0.5 mm， 对称开口环和金属线均采用金属铜， 铜线的电导率m=5.88 107s/m， 铜线厚度dm=0.018 mm， 开口环线宽均为 0.15 mm， 开口间隙均为0.1 mm， 单元结构的详细参数如图 2 和图 3 所示. 在用高频电磁仿真软件HFSS对该结构进行仿真时， 平面电磁波电场、 磁场极化方向如图 1 中所示， 为了在XOY平面模拟无限周期结构， 与Y轴垂直的两个平面设置为理想电边界(PEB)， 与X轴垂直的两个平面设置为理想磁边界(PMB)， 电磁波矢沿着Z轴平行于单元结构入射， 垂直于Z轴的两个面分别设置为输入与输出端口. 由于仿真过程存在限制， 这里采用相同大小的铜块作为理想开关来模拟导通状态[12,17]， 以此来研究所提出的结构在不同开关状态下仿真得到的电磁特性.

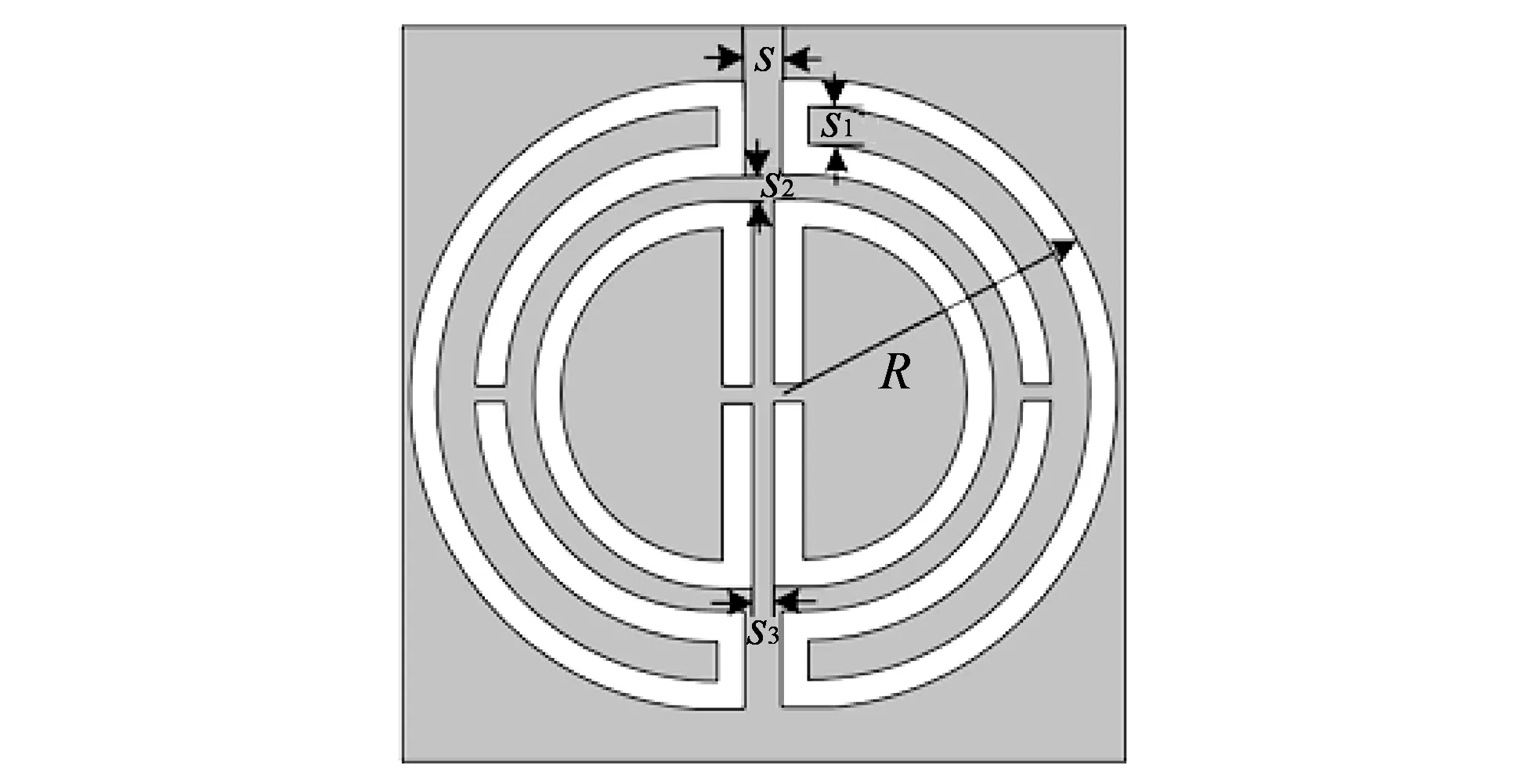
图 2 对称开口球结构图及其参数： s=s1=0.2 mm, s2=0.15 mm, s3=0.14 mm, R=1.7 mmFig.2 Sketch of symmetry SRRs with parameter markers: s=s1=0.2 mm, s2=0.15 mm, s3=0.14 mm, R=1.7 mm

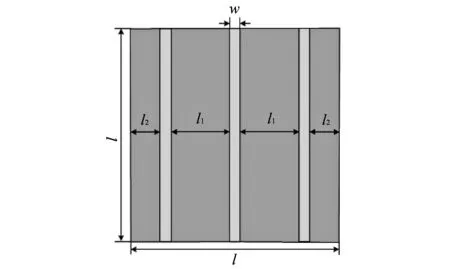
图 3 金属线结构示意图及其参数： w=0.2 mm, l=4 mm, l1=1.3 mm, l2=0.4 mmFig.3 Sketch of the thin-wires with parameter markers: w=0.2 mm, l=4 mm, l1=1.3 mm, l2=0.4 mm

2 可开关的双频段特性

磁谐振器由两组对称的开口环组成， 两个开口间隙对称地分布在每组开口环. 每个开口间隙处加载RF MEMS开关来控制其状态， 根据开口间隙处开关状态的不同， 结构可以分为多种不同的组合. 对全部的组合结构进行仿真之后发现3种组合形式0110， 1001， 0000(0代表开关处于截止状态， 1代表开关处于导通状态)分别能够实现低频、 高频和双频谐振， 3种结构如图 4 所示.

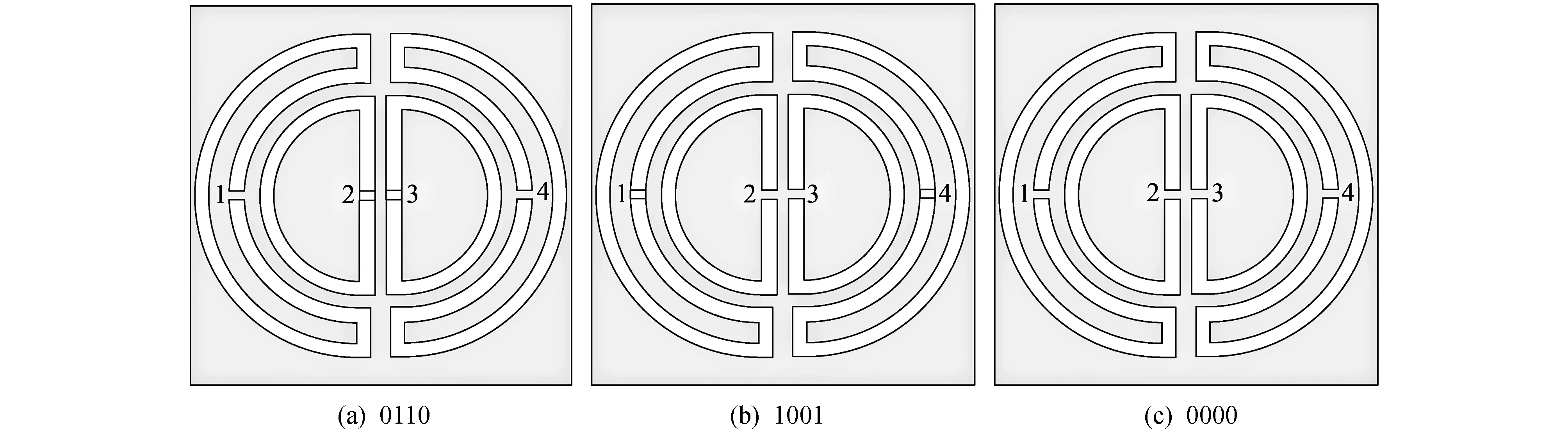
图 4 3种开关组合的结构示意图Fig.4 Topologies of the structure with three combinations of switches

2.1 低频谐振

当开关2和3处于导通状态， 开关1和4处于截止状态时， 研究此状态下的电磁特性： 在对该结构进行仿真之后， 得到了其传输特性曲线， 如图 5(a) 和图 5(b) 所示. 从图 5(a), 图 5(b) 中可以看出在 9～15 GHz 的频率范围内只存在一个电磁谐振， 并且在S21相位曲线的下陷点附近存在负折射频段， 这与Smith等人提出的推论相一致[18]. 采用文献[18]提出的方法从散射参数S11和S21提取出相应的介电常数、 磁导率和折射率， 结果如图5(c)～图5(e)所示. 从图5(c)～图5(e)中发现在 10.6～ 11 GHz 的频段范围内， 介电常数和磁导率同时为负， 折射率在10～11.1 GHz频段内为负值， 该结构能够在10.6～11 GHz范围内表现为左手特性. 为了进一步分析该谐振产生的原因， 提取了该结构在10.75 GHz处的表面电流图， 如图5(f)所示. 内环电流强度十分微弱， 外环出现很强的感应电流， 这说明入射波与外环在10.75 GHz附近相互作用产生了强的电磁谐振.

另外， 与经典的左手材料单元结构采用背面放置一条金属线不同[18]， 本文结构背面有3条金属线. 这是因为， 通过将金属线的数目从1条逐次增加到3条， 可以扩大负介电常数的频段范围， 在较宽的频段内实现负介电常数， 使得介电常数为负的频段和磁导率为负的频段重合， 从而出现负折射率， 实现左手特性.

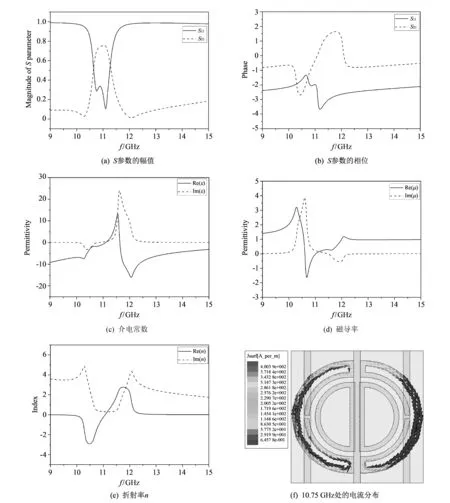
图 5 S参数及本构电磁参数随频率变化曲线Fig.5 Retrieved S-parameters and constitutive EM parameters

2.2 高频谐振

当开关2和3处于截止状态， 开关1和开关4处于导通状态时， 仿真得到的散射参数的幅值和相位曲线如图6(a)和图6(b)所示， 从传输谱来看， 该结构能够在14 GHz附近产生电磁响应. 从S参数提取的本构参数如图6(c)～图6(e)所示， 从图中我们发现在13.8～14.5 GHz的频段范围内， 介电常数和磁导率同时为负， 在13～14.6 GHz频段内折射率为负值， 在13.8～14.5 GHz范围内该结构表现为左手特性. 图4(f)给出了14.3 GHz附近的表面电流分布， 从中可以看出： 当开关1和4处于导通状态时， 外环原来的谐振特性被破坏， 电流强度十分微弱， 而内环仍然存在一定强度的感应电流， 由此表明14.3 GHz附近的电磁谐振是由入射波与内环相互作用产生的.

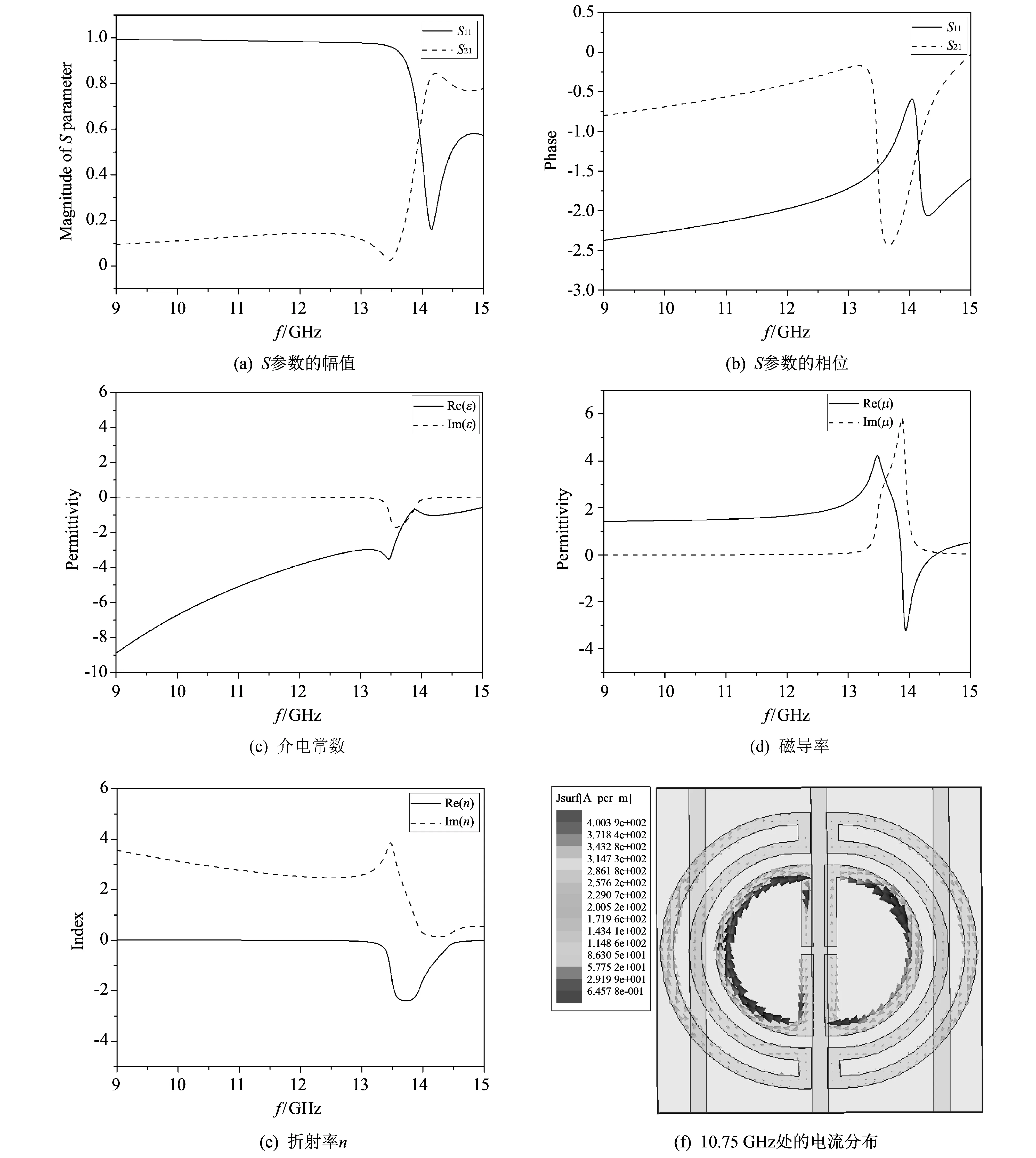
图 6 S参数及本构电磁参数随频率变化曲线Fig.6 Retrieved S-parameters and constitutive EM parameters

2.3 双频谐振

进一步研究了当所有开关均处于截止状态时所提出结构的传输谱曲线， 如图7(a)和图7(b)所示. 从图7(a)和图7(b)中可以看出， 该结构分别在10.6 GHz和14.3 GHz两个频率附近产生了谐振. 而且发现这两个谐振频段相比于之前结果发生略微移动， 这是由于当电磁波平行于单元结构入射时， 内外环之间存在着耦合作用. 图7(c)～图7(e)给出了此状态下的本构参数图， 从图7(c)和图7(d)中可以看出在频率范围10.5～10.8 GHz和14.2～14.4 GHz内， 介电常数和磁导率同时为负. 图7(e)表明折射率在9.8～10.9 GHz 和13.6～14.7 GHz范围内为负值， 该结构在10.5～10.8 GHz和14.2～14.4 GHz频段范围内表现为左手特性. 另外， 我们提取了10.75 GHz和14.3 GHz处的表面电流分布， 如 图8(a) 和图8(b)所示. 图8(a)中清楚地看到： 在10.75 GHz处外环中电流强度要比内环电流强度大， 外环发生强电磁谐振； 在图8(b)中14.3 GHz处的结果与图8(a)的情况正好相反， 外环电流强度十分微弱， 而内环产生强电磁谐振.

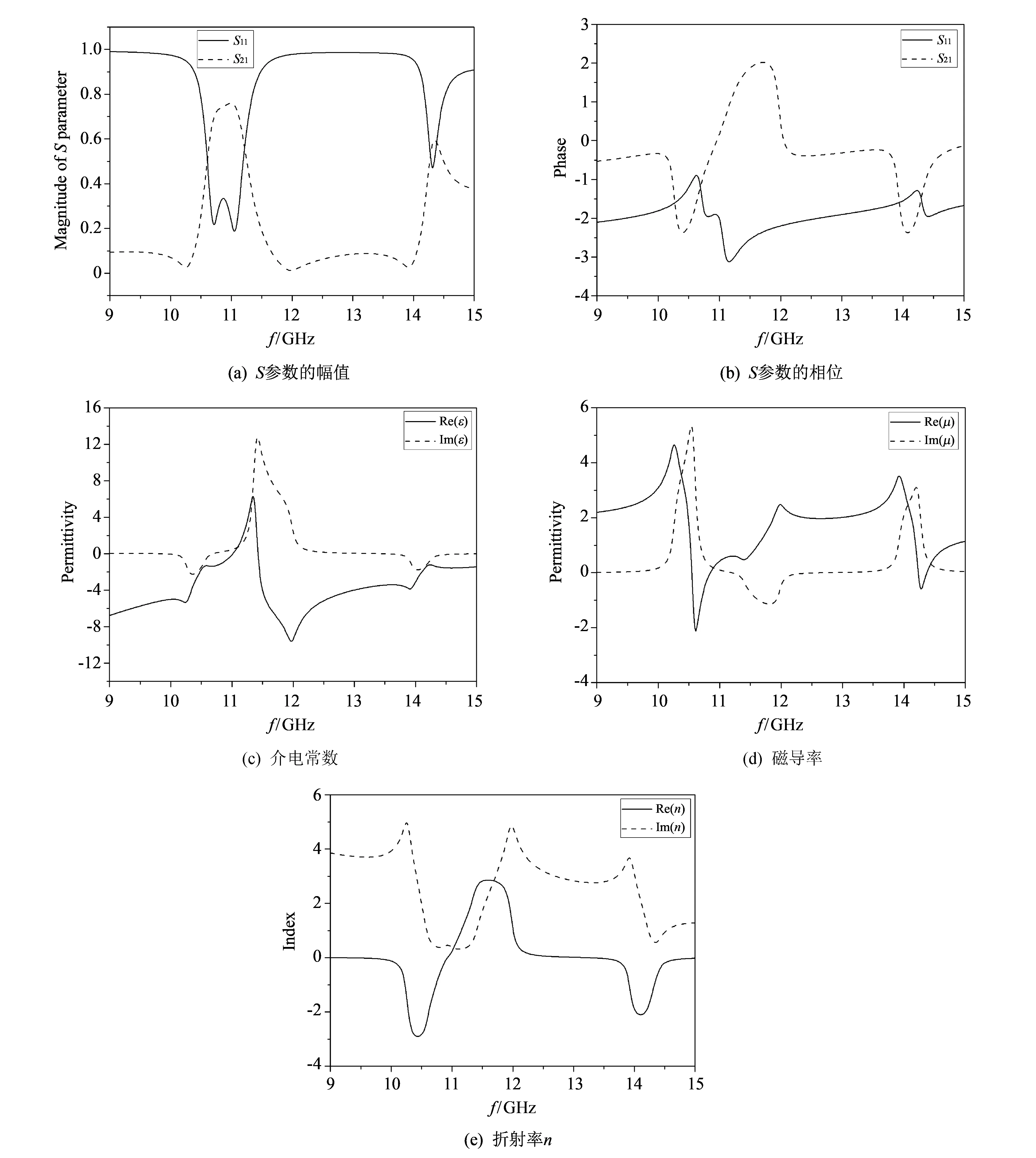
图 7 S参数及本构电磁参数随频率变化曲线Fig.7 Retrieved S-parameters and constitutive EM parameters

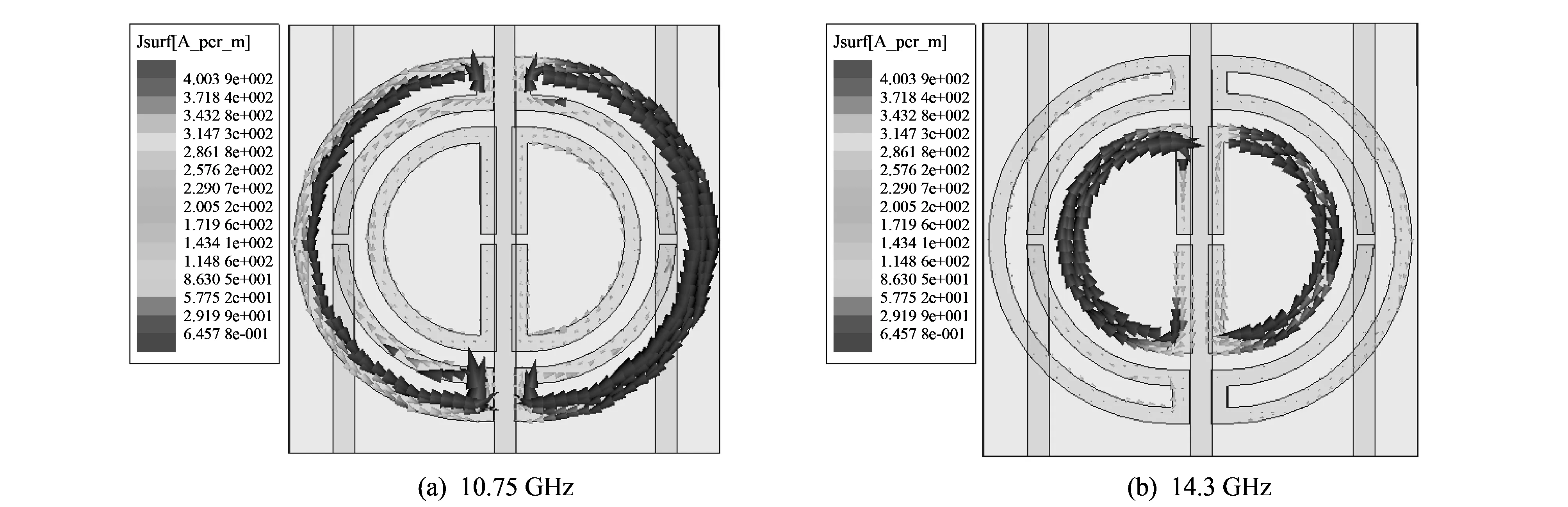
图 8 电流分布图Fig.8 Surface current distributions

3 结 论

本文设计了一种由两组对称开口环和3条金属线为单元结构的可开关双频段左手材料， 在内外开口环的开口处间隙处加载了4个RF MEMS开关， 通过控制4个开关的状态可以实现低频、 高频或高低频两个不同的频段的电磁响应. 研究发现： 当开关2和3处于导通状态， 开关1和4处于截止状态时， 该结构可以在10～11.1 GHz频段出现负的折射率， 在10.6～11 GHz范围内表现为左手特性. 当开关2和3处于截止状态， 开关1和4处于导通状态时， 该结构在13～14.6 GHz频段内折射率为负值， 在13.8～14.5 GHz范围内表现为左手特性. 当4个开关都处于截止状态时， 该结构在9.8～10.9 GHz和13.6～14.7 GHz范围内出现双频段的负折射， 在10.5～10.8 GHz和14.2～14.4 GHz GHz频段范围内表现为左手特性. 结果表明： 通过控制内环开关或外环开关状态能够相应地控制高频和低频谐振， 当两组开关全部处于截止状态时， 可以同时在内外环中产生强的磁响应， 同时实现高频和低频两个频段的负折射特性.

参考文献：

[1] Veselago V G. The electrodynamics of substances with simultaneously negative values ofεandμ[J]. Sov. Phys. Usp, 1968, 10(4)： 509-514.

[2] Pendry J B, Holden A J, Robbins D J, et al. Magnetism from conductors and enhanced nonlinear phenomena[J]. IEEE Trans. Microw. Theory Tech,1999, 47： 2075-2084.

[3] Smith D R, Padilla W J, Vier D C, et al. Composite medium with simultaneously negative permeability and permittivity[J]. Phys. Rev. Lett， 2000， 84(18)： 4184-4187.

[4] Shelby R A， Smith D R， Schultz S. Experimental verification of a negative index of refraction[J]. Science， 2001， 292(5514)： 77-79.

[5] Landy N I， Sajuyigbe S， Mock J， et al. Perfect metamaterial absorber[J]. Phys. Rev. Lett， 2008， 100， 207402.

[6] Pendry J B. Negative refraction makes a perfect lens[J]. Phys. Rev. Lett， 2000， 85(18)： 3966-3969.

[7] Sarkhel A， Mitra D， Paul S， et al. A compact meta atom for dual band negative permittivity metamaterial[J]. Microw. Opt. Technol. Lett， 2015， 57： 1152-1156.

[8] Sarkhel A， Mitra D， Chaudhuri R B. A compact metamaterial with multi-band negative-index characteristics[J]. Appl. Phys. A， 2016， 122： 471

[9] Faruque M R I， Hossain M J， Islam S S， et al. Design and analysis of a new double C-shaped miniaturized metamaterial for multiband applications[J]. Appl. Phys. A， 2017， 123： 310.

[10] Isi′c G， Vasi′c B， Zografopoulos D C， et al. Electrically tunable critically coupled terahertz metamaterial absorber based on nematic liquid crystals[J]. Phys. Rev. Appl， 2015， 3(6)： 064007.

[11] Kim H K， Lee D， Lim S. Frequency tunable metamaterial absorber using a varactor-loaded fishnet-like resonator[J]. Appl. Opt. ， 2016， 55(15)： 4113-4118.

[12] Bensafieddine D， Djerfaf F， Chouireb F， et al. Design of tunable microwave transmission lines using metamaterial cells[J]. Appl. Phys. A， 2017， 123： 248.

[13] Gui Yan， Yang Bin， Zhao Xiaoqing， et al. Angular and polarization study of flexible metamaterials with double split-ring resonators on parylene-C substrates[J]. Appl. Phys. Lett， 2016， 109： 161905.

[14] Geng Zhaoxin， Guo Xiangbin， Cao Yapeng， et al. Flexible， low-loss and large area metamaterials with high Q value[J]. Microelectron. Eng， 2015， 135： 23-27.

[15] Pitchappa P， Manjappa M， Chong Pei Ho， et al. Active control of near-field coupling in conductively coupled microelectromechanical system metamaterial devices[J]. Appl. Phys. Lett， 2016 ， 108： 111102.

[16] Pradhan B， Gupta B. Ka-band tunable filter using metamaterials and RF MEMS varactors[J]. J. Microelectromech. Syst， 2015， 24(5)： 1453-1461.

[17] Ekmekci E， Topallil K， Tayfun Akin， et al. A tunable multi-band metamaterial design using micro-split SRR structures[J]. Opt. Express， 2009， 17(18)： 16046-16058.

[18] Smith D R， Vier D C， Koschny Th.， et al. Electromagnetic parameter retrieval from inhomogeneous metamaterials[J]. Phys. Rev. E， 2005， 71： 036617.