基于BP-RBF组合神经网络的废气监测盲区SO2浓度预测

李晓云， 王晓凯

(山西大学 物理电子工程学院， 山西 太原 030006)

0 引 言

近年来， 工业园区作为工业企业的聚集地和各级区域工业发展的起动机， 在各地兴盛建立起来. 园区的空气质量不仅直接影响园区自身环境水平， 而且影响着所在区域甚至整个城市的大气环境. 2016年全国338个地级及以上城市中， 254个城市环境空气质量超标[1]， 全国范围内环境污染问题仍十分突出. 如何对工业园区内的大气进行有效监测， 对不同类型企业进行废气排放方面的有效管理， 已经成为园区环境管控乃至城市环境治理的重点工作. 目前， 国际上对污染气体排放的监测工作主要是对气体扩散模型的研究， 气体扩散模型分为环境模型和动态模型[2]， 最被广泛采用的静态环境模型包括高斯(Gaussian)模型、 BM模型、 Sutton模型和FEM3模型[3]. 不同的模型各有利弊， 在不同的场景中得到了广泛的应用[4-7]. Gaussian模型适用于非重气云扩散， 由于其提出时间较早， 研究较为全面， 因而得到了广泛应用. 高梦等[8]基于高斯模型对京津冀地区的空气污染问题进行研究， 得出了影响京津冀地区空气质量状况的主要污染源及污染参数； 何宁[9]等通过引入一种时间因子,对现有高斯烟团模型进行了改进,建立了以时间函数为动态变换基点的有毒气体扩散模型； 梁俊丽等[10]针对复杂地形条件， 基于传统大气扩散的高斯烟羽模型结合空间插值对原有算法进行了改进. 高斯扩散模式适用于均一的大气条件， 以及地面开阔平坦的地区， 适用于点源的扩散模式， 模拟精度相对不高， 无法模拟动态变化过程， 遇到复杂地形以及精度要求高的情况并不能很好的适用. 神经网络作为近年来的热点研究领域， 由于其具有很强的鲁棒性和容错性， 许多学者对气体扩散的研究由扩散模型转向神经网络的研究， 由此做了大量的研究工作. 冯樷[11]等人基于BP神经网络对天津市PM2.5浓度做了预测研究； 龚雪飞[12-14]等搭建了一种基于传感器阵列和BP神经网络相结合的多元有害气体检测系统； 陈洋[15]等基于无线传感器和BP神经网络对有毒气体检测提供了新的方法和思路； 薛宇[16]等提出运用径向基函数(RBF)神经网络方法实现对传感器检测过程中因环境温度变化所带来的测量误差进行补偿,提高了系统的检测精度. 神经网络由于其具有很强的学习能力， 在处理动态和突变数据方面相比扩散模型具有很大的优势， 因此近年来得到了较为广泛的应用. 本文基于BP-RBF组合神经网络建立了废气浓度预测模型， 该模型可以利用企业边界监测数据， 对监测盲区的SO2浓度进行精确的预测.

1 BP-RBF组合神经网络原理

图 1 BP-RBF组合神经网络结构图 Fig.1 BP-RBF combined neural network structure diagram

本文结合人工神经网络模型中最经典的误差反向传递(BP)模型[17]和径向基函数(RBF)模型[18]， 构建BP-RBF组合神经网络模型. 如图 1 所示， BP-RBF组合神经网络由BP神经网络和RBF神经网络两个子网构成.

1) BP 网络的学习分解为正向和反向学习两个过程： 正向传播过程， 给出输入信息， 通过输入层经隐含层逐层计算每个单元的实际输出值， 如若输出层未能得出期望输出， 即转入反向传播； 反向传播过程， 逐层递归地计算实际输出与期望输出之差， 并依据此差值来调节各层权值. 反复上述两个过程， 直至误差调整至误差满足要求时停止学习.

对于BP网络第i个样本输入， 隐含层有

ωjp*xp.

(1)

输出层有

ωoj*f(netj),

(2)

式中：ωjp为输入层与隐含层之间的连接权值；ωoj为隐含层与输出值之间的连接权值.

若期望输出为t， 当网络输出与期望输出不相等时， 存在误差

(3)

可以看出， 误差是权值ωoj,ωjp的函数， 权值修正公式为

(4)

(5)

式中：η为学习步长， 是一个常数， 0<η<1.

2) RBF网络与BP 网络在结构上基本相同， 区别在于RBF 网络隐含层节点传输函数为径向基函数， 即隐含层节点对输入产生局部响应. RBF网络有多种学习方法， 如随机选取中心法、 自组织学习中心法、 正交最小二乘法等， 学习过程分两个阶段： 一是自组织学习阶段， 求解隐含层基函数的中心与方法； 二是有导师学习阶段， 此阶段求解隐含层到输出层之间的权值.

径向基函数表现为多种形式， 常见的为高斯函数， 如式(6)所示

(6)

式中： ‖xp-ci‖为欧式范数;ci为高斯函数的中心;σ为方差.

隐含层到输出层的权值

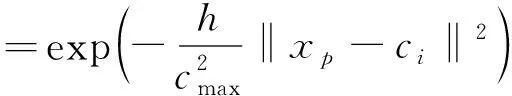
(7)

网络输出

(8)

2 监测盲区的SO2浓度预测

2.1 问题描述

图 2 园区边界布点简图Fig.2 Park boundary point sketch map

对工业园区进行废气监测， 首要问题就是进行监测布点， 通过对园区实地考察之后发现有些企业出于自身企业利益考虑， 对废气排放源头长期布点监测有很大抵触， 由此提出了通过企业边界布点监测数据来预测企业排放盲区SO2浓度的解决方案. 如图 2 所示， 为监测企业废气监测盲区SO2浓度， 在企业周围进行监测布点， 采用相同的时间间隔T对盲区周围监测点采集样本数据， 采集到的数据设为D(x1,x2,x3,…,xk)，xk表示采样数据， 废气源排放点(盲点)SO2浓度设为O， 本文要解决的问题就是找到这样一种映射关系f:D(x1,x2,x3,…,xk)→0， 本文提出的BP-RBF多层神经网络为寻找f找到了解决办法.

2.2 BP-RBF组合神经网络预测模型

根据通过边界监测数据预测推理盲区废气分布的总体解决思路， 建立BP-RBF组合神经网络预测模型. 在网络结构方面， 如前面图1所示， BP-RBF组合神经网络总体以5个边界监测点监测指标数据和当前时刻浓度作为输入， 以工业园区监测盲区的SO2浓度预测值作为输出. 具体来讲网络共分为两层， 第一层网络采用5个独立的BP网络， 分别以各个边界采集到的数据作为网络输入， 输出边界点的SO2预测浓度； 第二层网络采用RBF神经网络， 以第一层网络输出的5个边界点SO2浓度作为输入， 输出盲区的SO2预测浓度.

图 3 算法流程图Fig.3 Flow chart of algorithm

在网络结构选取方面， 第一层网络主要解决单点监测点的SO2浓度预测问题， 由于BP网络结构简单， 隐含层节点数目随着训练样本的增长变化不大， 在训练样本较多时， BP网络在复杂度和计算量上具有较大优势， 因此第一层网络选取BP网络. 第二层网络解决盲点SO2浓度数据监测问题， 因为输入数据来源于第一层网络的输出， 不可避免地引入了第一层网络的误差， 在进行第二层网络预测时误差相比于实际浓度会二次扩大， 再者， 在实际问题中由于盲点数据后期并不能实时监测， 网络参数并不能实时校正， 所以对误差提出了更高的要求， RBF网络是一种性能优良的前馈型神经网络， RBF网络可以以任意精度逼近任意的非线性函数， 具有全局逼近能力， 从而从根本上解决了BP网络的局部最优问题， 而且拓扑结构紧凑， 收敛速度快， 逼近精度高， 所以第二层网络采用RBF神经网络.

2.3 BP-RBF组合神经网络预测模型算法

对应的算法流程如图 3 所示， 算法描述如下：

1) 5个监测点独立采用5个BP神经网络对各监测点SO2浓度值进行预测， 然后对每个监测点做误差分析， 调整相关参数使之达到预期效果.

2) 以5个监测点SO2预测浓度值作为输入， 采用RBF神经网络预测盲区的SO2浓度值， 对监测盲区的SO2浓度预测值做误差分析， 总体误差分析效果不理想时还需要返回BP子网进行参数调整.

3 实验与结果

3.1 实际问题与数据准备

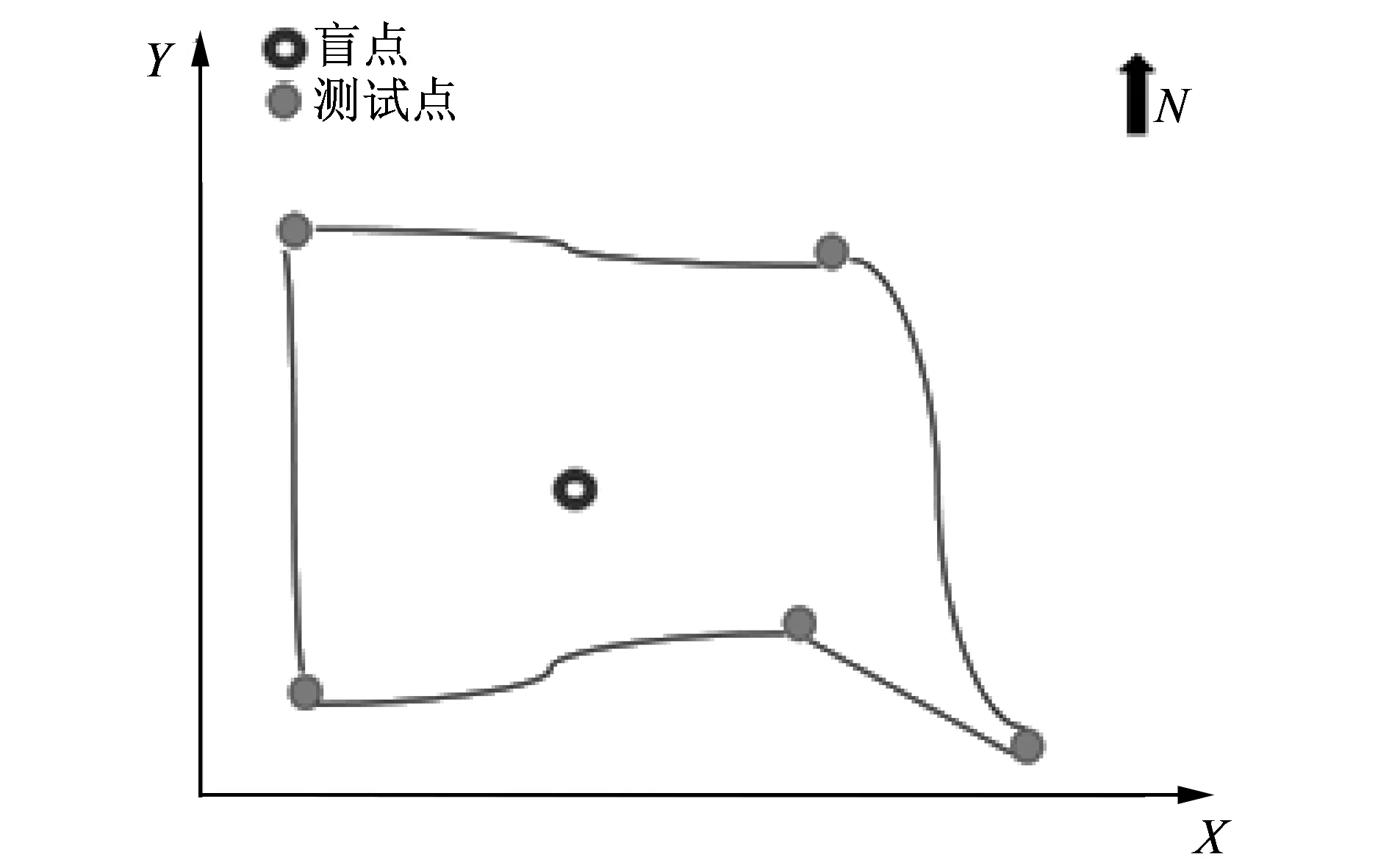
图 4 实际监测布点平面图Fig.4 Actual monitoring layout plan

本文以某市循环经济园区为研究目标， 选取某化工企业所排放SO2气体浓度为研究对象， 为了保证预测的准确性， 前期在监测盲区外围进行多点布点确定废气排放主导风向， 然后根据主导风向原则， 在监测盲点的上风向布置一个监测点， 在下风向布置两个监测点， 在下风向偏向45°方向各布一个监测点. 监测点布设情况如图 4 所示.

实验阶段实时监测了3月份连续15 d(每1 h记录一次)的变化数据， 在5个企业外围监测点采集湿度、 风速、 风向和大气稳定度4项指标数据和SO2浓度数据， 共有1 650 (330*5=1 650)组.

3.2 网络训练与测试

网络训练与测试分3步进行， 首先进行5个边界监测点BP神经网络的初步训练与预测， 不断优选最终确定14个隐含层节点数， 然后进行RBF神经网络的训练与预测， 最后进行BP-RBF神经网络的总体测试， 反复调节参数以达到预期预测效果. 每一步都以前220组数据作为训练， 后110组数据作为预测.

3.3 实验结果与分析

为衡量BP-RBF网络模型的稳定性和准确性， 选取平均绝对误差(MAE)、 平均绝对误差率(MAER)、 最大绝对误差(Emax)、 最小绝对误差(Emin)和预测准确度5个指标对网络进行评价， 规定Oi为真实值，Pi为预测值， 则各评价指标定义为：

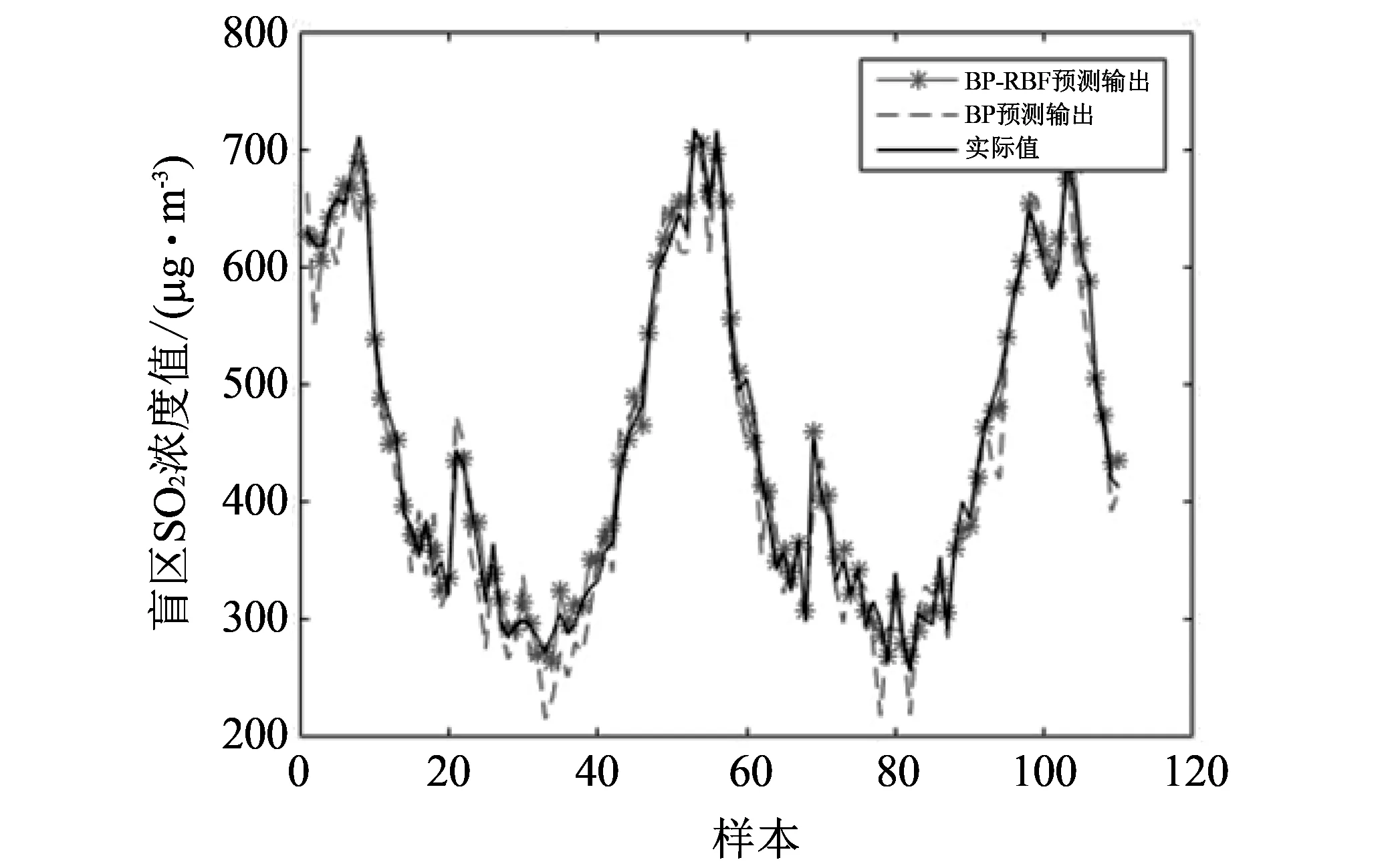
图 5 预测输出与实际值对比Fig.5 Comparison between predictive output and actual value

平均绝对误差

(9)

平均绝对误差率

(10)

本文对所提出的BP-RBF组合神经网络模型的预测结果与单一BP神经网络模型作了对比， 如图 5～图 7 所示， 可以看出BP-RBF多层神经网络比单一BP神经网络具有更好地跟随效果， BP-RBF网络预测值和实际值非常接近， 误差对比可以看出BP-RBF多层神经网络预测误差率控制到了0.1以下， 预测准确率达到了90%以上， 相比单一BP神经网络更好地达到了预测效果.

图 6 预测误差对比Fig.6 Comparison of error contrast

图 7 预测误差率对比Fig.7 Comparison of prediction error rate

表 1 给出了BP-RBF网络与单一BP网络评价指标对比， 由表 1 可以看出， 在预测准确性5项评价指标上， BP-RBF多层神经网络均优于单一BP网络预测， 预测误差率降到了4.167%， 预测准确度提高了5个百分点以上， 达到了95.833%， 达到了预期改进效果， 符合工业园区园区实际监测要求.

表 1 BP-RBF神经网络与单一BP神经网络评价指标对比

4 结束语

本文综合某市循环经济园区盲区无法直接监测的实际情况， 提出了在企业边界布点监测、 盲区废气浓度预测的BP-RBF组合神经网络模型. 出于计算量和复杂度考虑， 该模型第一层采用BP网络； 出于准确度考虑， 第二层采用RBF网络. 实验表明： 模型的预测准确度达到了95%以上， 为解决工业园区废气监测与管理问题提供了新的解决方案.

参考文献：

[1] 中华人民共和国. 2016年中国环境状况公报[S]. 2016.

[2] 顾子玲. 面向工业园区的污染气体排放监测系统设计[D]. 北京： 北京交通大学, 2016.

[3] 丁信伟， 王淑兰， 徐国庆. 可燃及毒性气体泄漏扩散研究综述[J]. 化学工业与工程， 1999， 16(2)： 118-122.

Ding Xinwei， Wang Shulan， Xu Guoqing. A review of studies on the discharging dispersion of flammable and toxic gases [J]. Chemical Industry and Engineering， 1999， 16(2)： 118-122. (in Chinese)

[4] Pan Xuhai, Jiang Juncheng, Wang Zhirong. Numerical analysis of diffusion process of flammable and toxic gases discharging accident[C]. International Symposium on Safety Science and Technology， Beijing: Chemical Industry Press, 2000: 297-301.

[5] 何宁. 有毒气体扩散模型在事故救援中的应用[J]. 自然灾害学报， 2009， 18(5)： 197-200.

He Ning. Application of poisonous gas diffusion models to rescue of chemical accidents [J]. Journal of Natural Disasters， 2009， 18(5)： 197-200. (in Chinese)

[6] Fero J， Carey S N， Merrill J T. Simulation of the 1980 eruption of mount St. Helens using the ash-tracking model PUFF[J]. Journal of Volcanology & Geothermal Research， 2008， 175(3)： 355-366.

[7] Pullen J， Boris J P， Young T， et al. A comparison of contaminant plume statistics from a Gaussian puff and urban CFD model for two large cities [J]. Atmospheric Environment， 2005， 39(6)： 1049-1068.

[8] 高梦， 朱家明， 刘新， 等. 基于高斯模型对空气污染扩散问题的研究[J]. 阜阳师范学院学报(自然科学版)， 2016， 33(2)： 12-16.

Gao Meng， Zhu Jiaming， Liu Xin， et al. Research of air pollution diffusion problem based on Gaussian model [J]. Journal of Fuyang normal University (Natural Science Edition)， 2016， 33(2)： 12-16. (in Chinese)

[9] 何宁， 吴宗之， 郑伟. 一种改进的有毒气体扩散高斯模型算法及仿真[J]. 应用基础与工程科学学报， 2010， 18(4)： 571-580.

He Ning， Wu Zongzhi， Zheng Wei. Simulation of an improved Gaussian model for hazardous gas diffusion [J]. Journal of Basic Science and Engineering， 2010， 18(4)： 571-580. (in Chinese)

[10] 梁俊丽， 孔维华， 费文华， 等. 基于复杂地形的高斯烟羽模型改进[J]. 环境工程学报， 2016， 10(6)： 3125-3129.

Liang Junli， Kong Weihua， Fei Wenhua， et al. Improvement of Gaussian plume model in complex terrain [J]. Chinese Journal of Environmental Engineering， 2016， 10(6)： 3125-3129. (in Chinese)

[11] 冯樷， 刘戈， 黄勇， 等. 基于BP神经网络的天津市PM2.5浓度预测研究[J]. 环境科学与管理， 2016， 41(6)： 121-125.

Feng Cong， Liu Ge， Huang Yong， et al. Research on Prediction of PM2.5 Concentrations in Tianjin Based on BP Neural Networks [J]. Environmental Science and Management， 2016， 41(6)： 121-125. (in Chinese)

[12] 龚雪飞， 徐景， 孙寿通， 等. PSO-BP神经网络在多元有害气体检测中的应用[J]. 传感器与微系统， 2015(2)： 154-156.

Gong Xuefei， Xu Jing， Sun Shoutong， et al. Application of PSO-BP neural network in multiple harmful gas detection [J]. Transducer and Microsystem Technologies， 2015(2)： 154-156. (in Chinese)

[13] 龚雪飞， 刘萍， 简家文. 基于PSO算法集成神经网络的多元有害气体检测系统[J]. 传感技术学报， 2015(6)： 938-942.

Gong Xuefei， Liu Ping， Jian Jiawen. Based on the integrated neutral-network optimized by PSO multiple harmful gas detection system[J]. Chinese Journal of Sensors and Actuators， 2015(6)： 938-942. (in Chinese)

[14] 龚雪飞. 基于集成神经网络的多元有害气体定量检测方法研究[D]. 宁波： 宁波大学， 2015.

[15] 陈洋， 张伯虎， 余缘敏. 基于无线传感器和BP神经网络的有毒气体检测[J]. 移动信息， 2015(2)： 19-20.

Chen Yang, Zhang Bohu, Yu Yuanmin. Toxic gas detection based on wireless sensor and BP neural network [J]. Mobile information， 2015(2)： 19-20. (in Chinese)

[16] 薛宇， 常建华， 徐曦. 基于RBF神经网络温度补偿的非色散红外SF_6气体传感器[C]. 全国集成光学学术会议, 2015.

[17] Ito Y. Representation of functions by super positions of a step or sigmoid function and their applications to neural network theory[J]. Neural Networks， 1991， 4(3)： 385-394.

[18] Park J， Sandberg I W. Universal approximation using radial-basis-function networks[J]. Neural Computation， 2014， 3(2)： 246-257.