应变扭矩的测量不确定度分析

张永祥， 明廷锋， 张 帅

(海军工程大学 动力工程学院， 湖北 武汉 43003)

应变扭矩测量就是将应变片粘贴在被测量的轴上(或安装于轴的夹具上)， 通过测量轴的扭转变形来测量转轴的扭矩. 对于扭矩测量， 国内外开展了广泛的研究， 提出多种测量方法[1-3]； 吴永烽[4]等提出了基于环形球栅扭矩测量原理的扭矩测量方法； 张海涛[5]提出了基于表面声波的动态扭矩测量系统； 吴素艳[6]提出了基于光纤光栅的扭矩测量系统； 吴召剑[7]提出了基于弹性联节器变形量检测的扭矩测量系统. 尽管这些方法新颖， 原理可行， 但至今尚未广泛推广使用. 目前， 国内外广泛使用、 性能稳定的扭矩测量是基于应变测量的扭矩测量系统. 对于应变扭矩的误差或不确定度， 已有很多学者开展了研究， 但主要是针对实验室中标准扭矩装置的不确定度分析. 姚明[8]开展了扭矩标准机测量结果的不确定度评定研究； 禹精达[9]开展了传动轴扭矩测量误差的影响因素分析； 陈永培[10]在研制高精度扭矩标准机的同时， 分析了标准机的测量不确定度. 对于工程上应变扭矩的测量不确定度， 还没有系统定量地进行分析研究. 本文从应变扭矩测量原理入手， 对影响扭矩测量不确度的因素及测量不确度进行了深入的研究.

1 应变扭矩测量原理

应变扭矩测量时， 首先将应变片粘贴于被测扭矩的转轴上， 应变片布片的方式很多， 常见的粘贴方式由如图 1 所示， 有3种方式， 3种方式各有特点. 将4片应变片构成差动全桥， 如图 2 所示. 图 2 中R1,R2,R3,R4为4片应变片的电阻，E0为桥压，u为应变电桥的输出电压. 输出电压u经调理后由发射电路无线发射(信号调理和发射安装于转轴上)， 地面接收装置实时接收转轴上的应变信号， 经处理后得到扭矩信号.

图 1 转轴应变片粘贴形式Fig.1 Rotating axis strain measurement paste form

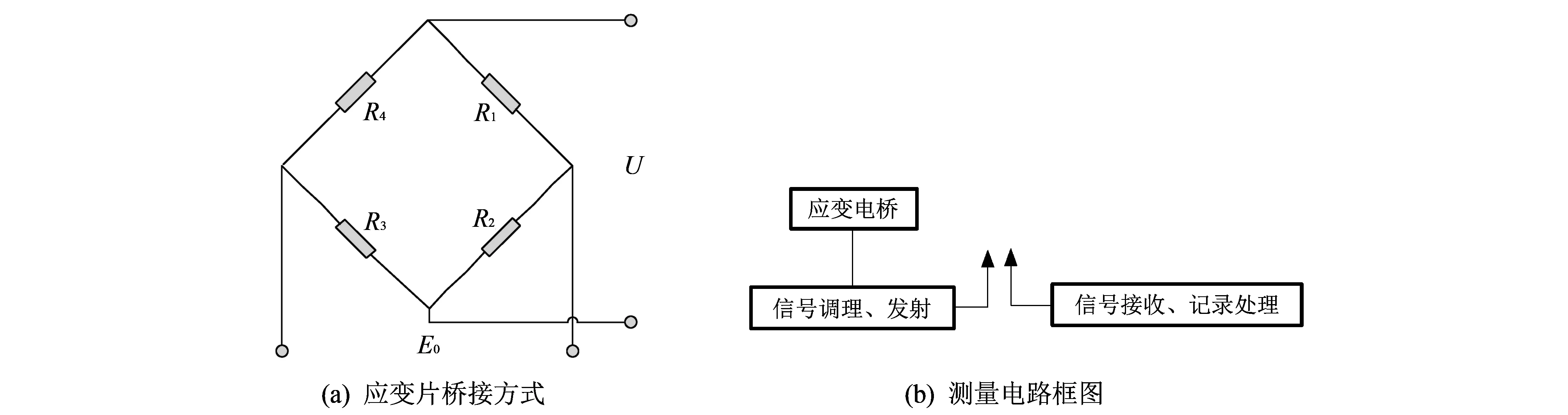
图 2 应变遥测原理Fig.2 Strain telemetry principle

对于被测转轴， 当受到一定的扭矩作用时， 必然会产生扭转变形， 其主应力方向与轴线呈45°. 假设4片应变片受到的应变分别为ε1,ε2,ε3,ε4， 由受力分析可知ε1=-ε2=ε3=-ε4=ε. 则应变电桥的输出电压

ε1-ε2+ε3-ε4)=E0Ksε,

(1)

式中：Ks为应变片的灵敏度.

电桥输出电压经调理， 无线发射、 接收到的电压

U=K1u=E0KsK1ε,

(2)

式中：K1为调理发射接收的增益. 由式(2)得

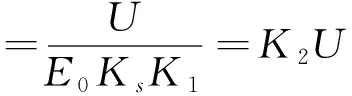
(3)

式中：K2为应变测试的应变灵敏度系数.

假设转轴的抗扭截面模量为Wn； 轴材料的弹性模量为E； 泊松比为μ； 则转轴的扭矩

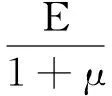
(4)

因此应变扭矩的测量原理是： 通过应变片测量转轴的应变， 经电桥变换及放大滤波等调理得到随应变变化一致的电压， 标定后得到以之对应的应变， 根据扭矩应变式(4)， 计算得到转轴扭矩.

2 扭矩的测量不确定度分析

从式(3)， 式(4)可以发现， 应变扭矩测量的不确定度可分为两部分进行分析， 一是应变测量引起的不确定度； 二是由式(4)计算扭矩时，E，μ，Wn，ε引起的扭矩测量不确定度.

2.1 应变的测量不确定度

应变的测量不确定度主要来自以下几个方面： ① 应变本身的不确定度； ② 粘贴应变片引起的不确定度(包括贴片方式、 应变电桥构成)； ③ 测量仪器引起的不确定度.

2.1.1 应变片引起的应变测量不确定度

应变片由于制造的原因， 其灵敏度存在不确定性. 目前国内常给出应变片的灵敏度最大允许误差为±α%， 假设灵敏的不确定度呈均匀分布， 由式(3)， 灵敏度造成的应变测量不确定度为

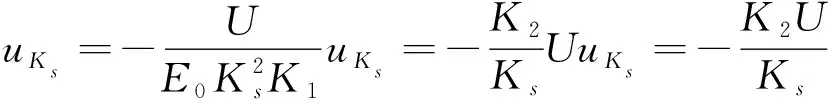
(5)

2.1.2 测量仪器引起的应变测量不确定度

根据JJG623-2005电阻应变仪检定规程， 用于测量扭矩的动态应变仪所引起应变测量不确定的主要有： 应变仪的示值误差、 非线性误差、 零点漂移、 示值稳定性. 如 0.2 级动态应变仪， 示值误差为±( 0.2%读数±2 με)、 非线性误差(FS)为±0.05%、 零点漂移为(2 h)±2 με， 示值稳定性为(2 h)±0.05%， 则仪器引起的应变测量不确定度为

(6)

2.1.3 贴片引起的应变测量不确定度

对于第1种贴片方式(如图 1(a))， 由式(1)电桥输出的电压

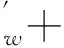
(7)

对于第2种贴片方式(如图 1(b)， 由式(1)电桥输出的电压

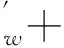
(8)

对于第3种贴片方式(如图1(c))， 由式(1)， 电桥输出的电压

ε+εl+εw+εt)-(-ε+εl+εw+εt)+(ε+εl-εw+εt)-

(-ε+εl-εw+εt)]=E0Ksε.

(9)

从上述3种贴片方式可以发现： ① 具有温度补偿功能， 不管环境温度如何变化， 由应变片本身及贴片引起的附加温度εt会自动消除； ② 能自动消除转轴受到位压、 弯曲力作用， 只测量扭矩产生的应变.

尽管按上述3种方式贴片具有温度补偿、 消除轴受拉压和弯曲的影响， 但贴片误差还是会引起应变测量不确定度. 实际粘贴应变片时， 不可能完全将应变片丝毫不差地贴在±45°方向， 假设偏离β度， 贴片按图 1(b)， 则产生的应变测量不确定度

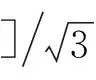
(10)

由以上分析可知， 应变的测量不确定度

(11)

2.2 扭矩的测量不确定度

由式(4)可知， 扭矩测量不确定度由Wn,E,μ,ε4个因素组成.

2.2.1 抗扭截面模量Wn引起的扭矩不确定度

根据材料力学， 对于一根外径为D， 内径为d的转轴， 其抗扭矩截面模量

πD3(1-α4),

(12)

式中：α=d/D. 如果转轴的尺寸能精确确定， 则Wn不会引起扭矩测量的不确定度. 反之， 如果仅给转达轴内径、 外径的加工尺寸及公差， 则由Wn引起的不确定度

(13)

式中：Wnmax,Wnmin为由尺寸公差计算得到的最大和最小抗扭截面模量.

2.2.2 转轴材料弹性模量和泊松比引起的扭矩测量不确定度

扭矩测量的合成不确定度

(14)

式中：uE为转轴材料弹性模量引起的扭矩测量不确定度；uu为泊松比引起的扭矩测量不确定度.

扭矩测量扩展不确定度

u=K·uc(k=2).(15)

3 扭矩测量不确定度实例分析

1) 应变的测量不确定度

根据已知条件可得Wn=4.454 9×10-4m3，Wnmax=4.532 9×10-3m3，Wnmin=4.454 9×10-4m3

.532×10-6,

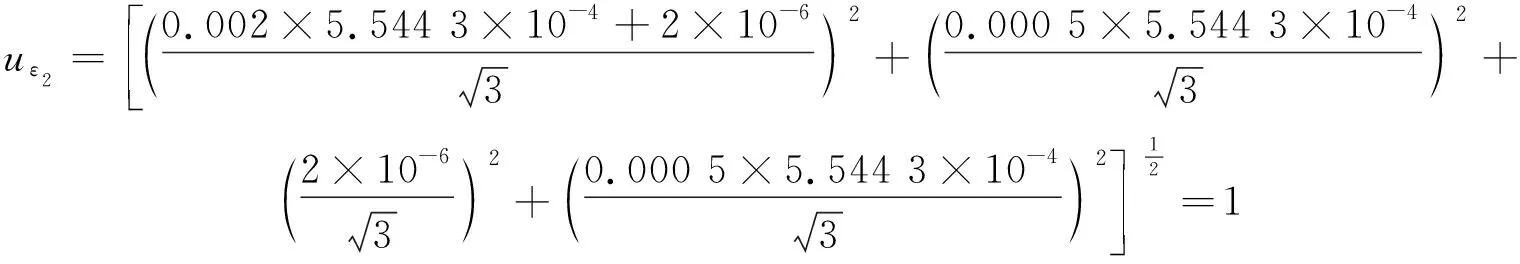
假设应变片的最大贴片误差为5°， 则

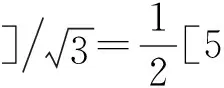
应变的测量不确定度为

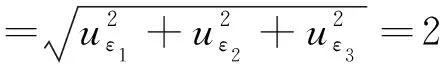
2) 扭矩的测量不确定度

.251 66×10-6m3,

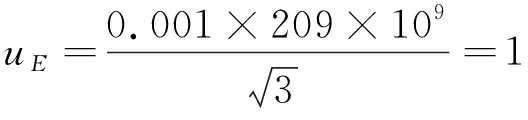
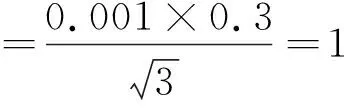
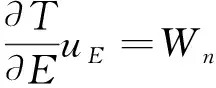
扭矩的合成不确定度

3) 扭矩的扩展不确定度

U=Kuc=2×351.47=702.93 N·m.

扭矩

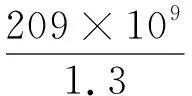
扭矩的测量结果为(39 708.88±702.93) N·m， (k=2).

4 结 论

从上面的实例和理论分析可以发现， 引起扭矩测量不确定度的主要因素有：

1) 应变片灵敏度、 测量仪器准确度以及贴片不准确都会引起应变测量不确定度， 其中最主要的是应变片灵敏度和仪器准确度， 贴片引起的不确定度要小得多.

2) 转轴尺寸测量不准是引起扭矩测量不确定度的主要因素之一， 该因素可通过准确获得尺寸而消除.

3) 转轴材料弹性模量的不确定度也是引起扭矩测量不确定度的主要因素， 而泊松比的不确定度对扭矩测量影响相对较小. 提高材料弹性模量的测量准确度， 可显著降低扭矩测量的不确定度.

4) 消除转轴尺寸不确定度， 降低材料弹性模量的不确定度， 可显著降低扭矩测量的不确定度.

参考文献：

[1] 王登泉, 杨明, 叶林， 等. 非接触式旋转轴扭矩测量现状[J]. 电子测量技术, 2010， 33(6)： 8-12.

Wang Dengquan， Yang Ming， Ye Lin， et al. Study of non-contact torque measurement of rotating shanft[J]. Electronic Measurement Technology， 2010， 33(6)： 8-12.(in Chinese)

[2] 黄兴伟. 具有无线传输功能的数显扭矩测量系统的研究与开发[D]. 浙江： 浙江大学， 2012.

[3] 吕华溢， 杨军， 宋娜. 轴系扭矩测量方法与发展趋势[J]. 计测技术， 2017， 37(2)： 6-10.

Lv Huayi， Yang Jun， Song Na. The methods and development trend of torque measurement for transmission shafting[J]. Metrology & Measurement Technology， 2017， 37(2)： 6-10.(in Chinese)

[4] 吴永烽， 喻洪麟， 何安国. 环形球栅扭矩测量原理研究[J]. 仪器仪表学报， 2010， 31(11)： 2580-2584.

Wu Yongfeng， Yu Honglin， He Anguo. Research on the measuring principle of torque based on ring ball gratings[J]. Chinese Journal of Scientific Instrument， 2010.31(11)： 2580-2584.(in Chinese)

[5] 张海涛， 唐敦兵， 许芹. 基于声表面波的车辆驱动轴动态扭矩测量系统研究[J]. 农业机械学报， 2014， 45(10)： 29-33.

Zhang Haitao， Tang Dunbing， Xu Qin. Measurement system of vehicle drive Shaft dynamic torque based on SAW[J]. Transactions of the Chinese Society for Agricultural Machinery， 2014， 45(10)： 29-33.(in Chinese)

[6] 吴素艳， 黄银国， 赵美蓉等. 基于光纤光栅的扭矩测量系统设计[J]. 纳米技术与精密工程， 2017， 15(2)： 135-139.

Wu Suyan， Huang Yinguo， Zhao Meirong， et al. Design of torque measurement system based on FBG[J]. Nanotechnology and Precision Engineering， 2017， 15(2)： 135-139.(in Chinese)

[7] 吴召剑， 吴定祥， 龚金成， 等. 基于弹性联轴器形变量检测的电机扭矩测试系统[J]. 传感器与微系统， 2016， 35(4)： 116-122.

Wu Zhaojian， Wu Dingxiang， Gong Jincheng, et al. Motor torque measurement system based on elastic couplings deformation detection[J]. Transducer and Microsystem Technologies， 2016， 35(4)： 116-122. (in Chinese)

[8] 姚明， 费跃. 扭矩标准机测量结果的不确定度评定[J]. 价值工程， 2014(2)： 319-320.

Yao Ming， Fei Yue. Uncertainty evaluation for the measurement results of torque standard machine[J]. Value Engineering， 2014(2)： 319-320. (in Chinese)

[9] 禹精达， 朱晖. 传动轴扭矩测量误差分析[J]. 机械研究与应用， 2011(4)： 4-5.

Yu Jingda， Zhu Hui. Measurement error anaysis of shaft torque[J]. Mechanical Research & Application， 2011(4)： 4-5. (in Chinese)

[10] 陈永培， 林杰俊， 倪晋权， 等. 1 kN·m 高精度扭矩标准机的研制[J]. 机电一体化， 2016(9)： 63-67.

Chen Yongpei， Lin Jiejun， Ni Jinquan， et al. The develop of 1 kN·m high torque standard device[J]. Mechatronics， 2016(9)： 63-67. (in Chinese)