基于改进的三段式永磁同步电机启动方法

陶 鑫， 庄哲民， Alex Noel Josephraj， 黄慕斌， 高 伟

(1. 汕头大学 电子工程系， 广东 汕头 515063； 2. 汕头杰泰电子科技有限公司， 广东 汕头 515041)

0 引 言

永磁同步电机(permanent magnet synchronous motor， PMSM) 具有功率密度大、 控制性能好、 功率因数高、 动态响应快等优点， 在家用电器、 工业伺服、 电动汽车、 4旋翼无人机等领域得到了广泛的应用[1]. 对于PMSM控制系统， 启动过程的动态响应对电机系统性能有重要影响， 特别是在低速、 零速启动等关键环节. 为了实现平滑无冲击的启动过程， 需要精准的转子位置和速度信息. 这些信息通常由光电编码器、 旋转变压器、 霍尔传感器等位置传感器获取， 但这类位置传感器的存在增加了系统的成本和复杂性， 也使得系统对机械振动和温度等环境因素的抗干扰能力降低， 从而降低了系统的可靠性， 因此PMSM的无位置传感器控制方案成为了电机控制领域的研究热点之一.

对于基于无位置传感器的PMSM启动， 研究人员提出了多种位置估测算法. 文献[5]提出了稳定V/f 控制方法， 通过探测无功功率的快速变化对频率进行反馈实现稳定控制， 但在大转矩快速启动场合中， 电流无法得到有效控制， 启动过程中可能出现过流的情况； 文献[3]提出高频注入法， 向电机定子绕组中注入高频正弦信号， 通过检测定子电流中的高频信号成分获取转子位置信息. 这种方法信号处理过程复杂， 对硬件要求高， 并且需要使用滤波器， 会带来时间延迟和幅值畸变； 为了解决这一问题， 文献[8]提出使用高频方波信号代替高频正弦波信号注入到电机中， 并且给出了几种可以注入的方波类型. 但是高频注入对信号检测精度要求较高， 计算过程复杂， 需要多个滤波器且时延较长， 并且高频电流的存在也会对控制性能造成一定的影响.

本文针对上述启动问题， 提出一种改进的基于电流幅值变斜率递减的3段式控制方法. 采用电流闭环预定位法获得转子初始位置信息； 在加速阶段采用I/F速度开环、 电流闭环的控制方法， 实现带载情况下的快速启动； 在状态转换过程中提出采用基于电流幅值变斜率递减的方法， 可以让电机平滑地完成从I/F控制至Luenberger观测器[6]控制的切换. 仿真实验表明： 该方案有效可行， 具有一定的实际应用价值.

1 启动过程分析

为了更好地分析PMSM的启动过程， 有必要建立PMSM电机数学模型对相关过程加以描述， 在电机同步d-q坐标系下， PMSM的电压方程可表示为

(1)

PMSM的磁链方程可表示为

(2)

式中：RS为定子每相绕组的等效电阻；p为微分算子；ωs为转子角速度；ψjM为转子磁链幅值；ud,uq,id,iq,Ld,Lq,ψd,ψq分别为同步坐标系d-q下的电压、 电流、 电感和定子磁链.

由式(1)， 式(2)可得表贴式永磁同步电机电磁转矩方程为

ψfMiq,

(3)

式中：n为电机极对数， 由式(3)可知， 电机磁阻转矩与电磁转矩可由d-q坐标轴下电流id,iq分别控制. 基于同步坐标系的启动过程主要对d,q轴电流进行控制， 而采用电流闭环的方式可以有效地避免过流现象发生.

一般而言， PMSM的启动过程分为基于电流闭环预定位、 I/F加速启动、 状态切换3个阶段.

1.1 基于电流闭环预定位

在PMSM启动初期的零速以及低速区域， 由于观测器精度不够导致转子的位置和速度信息估算偏差过大， 因此需要先将电机转速提升至观测器观测范围内， 然后切换到Luenberger观测器控制.

图 1 转子预定位示意图Fig.1 Sketch map of rotor pre-positioning

假设初始时刻电机静止， 转子转速为零且转子位置信息无法得知， 需要对转子进行预定位， 将转子牵引到设定位置获取初始位置信息. 预定位法是向PMSM的定子施加一个固定方向的电压矢量， 电压矢量会在该矢量方向上产生磁势. 转子永磁体本身存在一个转子磁势， 该磁势方向为电机同步坐标系d轴方向. 由于定子磁势与转子磁势存在夹角， 因此会产生作用力将转子拖动到电压矢量的方向， 从而实现转子初始位置估计. 为了防止出现过流现象， 采用电流闭环的转子预定位法. 由于已经进行了电流闭环， 矢量电流id能够跟踪给定值idref，idref为一个常数，q1轴电流i1保持为零， 转子预定位示意图如图 1 所示.

由图1(a)所示， 定位前转子位置随机， 通过控制矢量电流id来产生一个方向为d2、 幅值可控的定子磁势. 由于定子磁势与转子磁势存在夹角α， 将产生相互作用力使转子N极定位于定子磁势方向d2. 为了让电机能够快速启动， 我们使d1-q1坐标系的初始位置滞后于电机d-q坐标系初始位置90°， 即预定位阶段将电流矢量id定位在d1-q1坐标系的交轴q1的位置， 转子定位后的位置如图1(b)所示.

1.2 I/F加速启动

转子定位成功后开始加速启动过程， 为了满足不同负载都能平滑启动， 这里采用I/F流频比控制方法. I/F启动的基本思想是在电枢绕组中施加一个旋转的电流矢量， 通过该电流矢量在力矩轴的投影分量产生电磁转矩拖动电机运行直至电机转子位置与电流矢量之间保持一个相对静止的稳定运行状态.

I/F控制运行在速度开环、 电流闭环状态下， 设定d1轴电流id保持为零，q1轴电流iq跟踪给定值iqref，iqref为常数. 电机转速采用斜率给定方式， 将转子速度积分就可以得到转子位置θ， 经过控制系统运算后更新电压矢量， 从而牵引转子平滑启动， 加速启动阶段给定d1-q1坐标系与电机d-q坐标系位置关系示意图， 如图 2 所示.

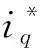
(4)

由式(4)可以看出， 电机在I/F控制阶段能在一定范围内进行转矩自调整. 当θr∈[0,π/2]时， 若电磁转矩Tem过小， 则电机转子会滞后，θr变小， 而iq保持不变， 根据式(4)可知Tem会增大， 电机加速至期望位置达到新的平衡. 若Tem过大， 调整过程类似. 因此， 当给定电流iq足够大时，θr会在[0,π/2]之内变化以调整电磁转矩大小， 保证电机在不同负载情况下都能顺利地快速启动. I/F控制具有转矩-功角自平衡特性， 因此具有一定的抗负载扰动能力.

1.3 状态切换

当转子转速升高到一定程度后， 观测器可以较为精准地观测转子转速和位置信息， 此时可以从I/F控制切换到Luenberger观测器. 但是电机转子实际位置角与I/F给定位置角之间存在角度偏差θr， 如果直接进行切换， 在切换时刻必然导致q轴给定电流与q轴反馈电流不匹配， 会造成电机转速振荡和电流突变， 从而可能导致电机启动失败.

为了实现平滑过渡， 需要采取合适的切换方法. 文献[10]设计出一种iq调节器使θr趋向于零， 当θr小于设定的阈值时进行状态切换. 根据转矩-功角自平衡特性， 当减小给定q1轴电流时， 投影在电机q轴的电流也会减小， 导致电机速度减小， 相角差θr减小， 当给定电流与新的相角差在力矩轴上产生的投影与负载转矩平衡时调整过程结束. 相角差θr减小到设定阈值时， 给定坐标系d1-q1与电机实际坐标系d-q基本重合， 此时电机可以平滑地从I/F控制切换到Luenberger观测器.

上述方法系统运行在转矩-功角自平衡的边缘区域， 电流调节器若设置不合理对相角差θr有很大影响， 并且θr如果变成负值， 电机会有失步风险. 其次， 这种方法需要较长的电流调节过程， 实用性和可靠性并不十分理想.

针对上述方法存在的问题， 本文提出一种基于电流幅值变斜率递减的方法， 让电机可以平滑无冲击地过渡到Luenberger观测器.

2 基于电流幅值变斜率递减的状态切换

由式(4)可知， 电磁转矩的大小决定于给定电流矢量在电机q轴上的分量， 在恒定速度运行状态下， 如果减小q轴给定电流， 在减小电流的瞬间， 电机的自调整过程会使得θr减小， 直到电机达到新的平衡状态. 假设切换开始时刻为t0， 完成时刻为t1， 电流矢量变化函数与角度差函数的斜率分别为ki,kθ， 则在t0到t1时间间隔中， 电流矢量和角度差变化方程为

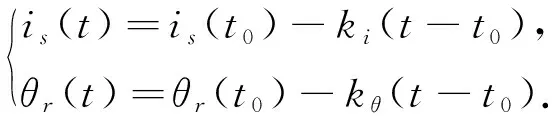
(5)

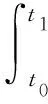
(6)

由式(5)， 式(6)可得ki与kθ关系表达式为

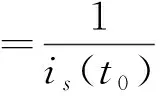
(7)

由式(7)可知， 在相位差初始角θr(t0)与电流初始值is(t0)一定的条件下，kθ与ki成正比， 增大ki可以使θr更快趋近于零. 为了让电机快速启动， 电流变化斜率ki值应设置很大， 但由于机械系统的响应速度远慢于电流下降的速度， 可能导致电机在调节过程中还未重新达到新的平衡位置便进入下一个调节周期. 这样会产生很大的电流脉动， 使得电机转速有很大抖振， 严重的甚至会影响观测器估算， 导致启动失败. 为了兼顾快速启动和切换过程平滑， 本文提出一种变斜率的电流幅值递减方法， 即斜率采用二次函数K(ωs)来实现.

电流递减斜率函数

(8)

式中：km为常量；ωmin,ωmax为设定观测器估算速度收敛的上下限值. 电流矢量方程可以表示为

is(t)=is(t0)-K(ωs)(t-t0).

(9)

在过渡开始时，ωs较小， 电流变化率大， 电流下降快； 在过渡后期，ωs较大， 电流变化率小， 电流下降缓慢， 电流调节过程中不会出现较大的电流脉动. 采用变斜率的电流递减法可以让状态切换过程时间大大缩短， 在切换瞬间不会出现较大的电流脉动对电机运行造成影响， 系统控制原理框图如图 3 所示.

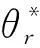
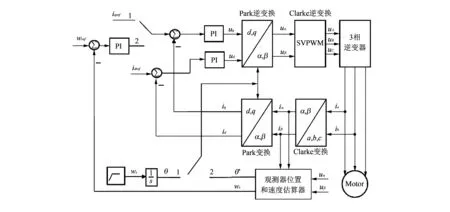
图 3 系统控制原理框图Fig.3 Block diagram of system control principle

3 实验结果

本控制系统实验选取STM32F103ZET6作为主控， 搭建低成本的32 b ARM硬件控制平台， 芯片主频为72 MHz， 有512K闪存、 64 Kb RAM， 能够满足实现无位置传感器算法的要求. 电机启动时采用电流闭环预定位法， 定位成功后I/F控制电机加速启动， 从观测器检测速度收敛到状态切换过程， 采用电流幅值变斜率递减的方式让电流快速下降并且在切换点不会产生较大电流脉冲. 实验仿真所采用电机参数如表 1 所示.

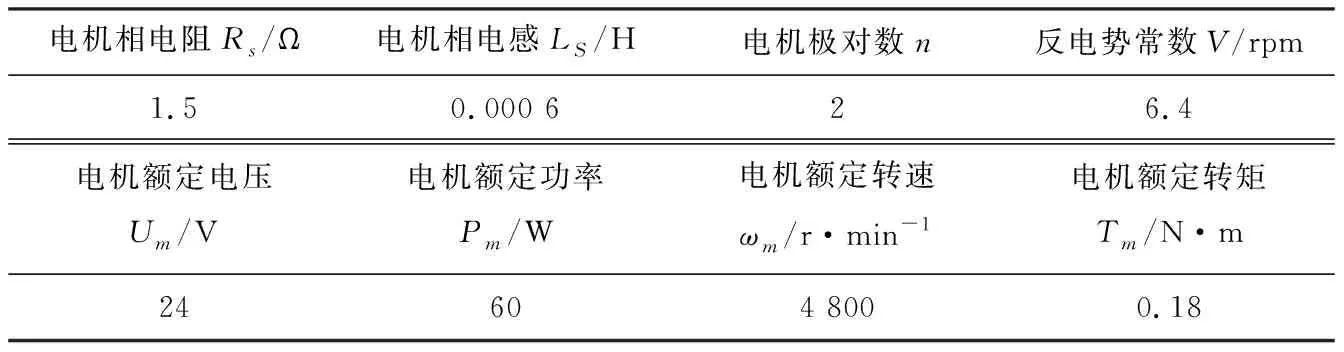
表 1 电机参数

实验采取两种方案， 改进前方案观测器速度收敛时直接切换到Luenberger观测器， 改进后采用电流幅值变斜率递减方法对切换过程进行处理. 电机带载转速曲线如图 4 所示， 转速值由观测器测得， 在状态切换过程中，q轴电流变化波形如图 5 所示.

由前述所知， PMSM启动过程由预定位、 I/F加速启动、 状态切换3个部分构成. 在预定位阶段， 通过图4的转速曲线可知， 预定位需要大约0.3 s的时间. 由于采用电流闭环的预定位法牵引电机转子到设定位置， 得到初始转子位置信息， 所以在定位过程中电流可控不会产生过流现象.

定位完成后进入加速阶段， 由图4可以看出在0.3～0.9 s期间， 两种方法由观测器观测到的PMSM转速有一定的波动， 速度增长趋势与斜坡给定速度基本吻合， 加速度基本恒定. 由此可见， 在I/F加速启动阶段带载情况下能顺利地快速平滑启动， I/F自稳定特性具有一定的抗负载扰动能力. 在0.9s处观测器观测速度收敛， I/F加速启动阶段完成， 此时进入状态转换阶段.

在状态转换阶段中， 由图4可见， 改进前直接切换方案在转速控制上出现超调与抖动， 而采用基于电流幅值变斜率递减的改进方案后， 切换后转速基本控制在800 r/min附近， 没有出现较大的速度振荡， 具有较高的鲁棒性. 同样从图5的轴电流波形可以看出， 在状态切换的0.9～1.2 s区间内， 改进前方案电流变化波动较大， 产生了较大的电流脉冲使得电流出现震荡， 进而使得PMSM的转速出现震荡； 而改进后方案前期电流依然保持较大的变化率及较快的电流下降速度， 但后期电流变化率小， 电流冲击几乎被消除， 切换过程平滑.

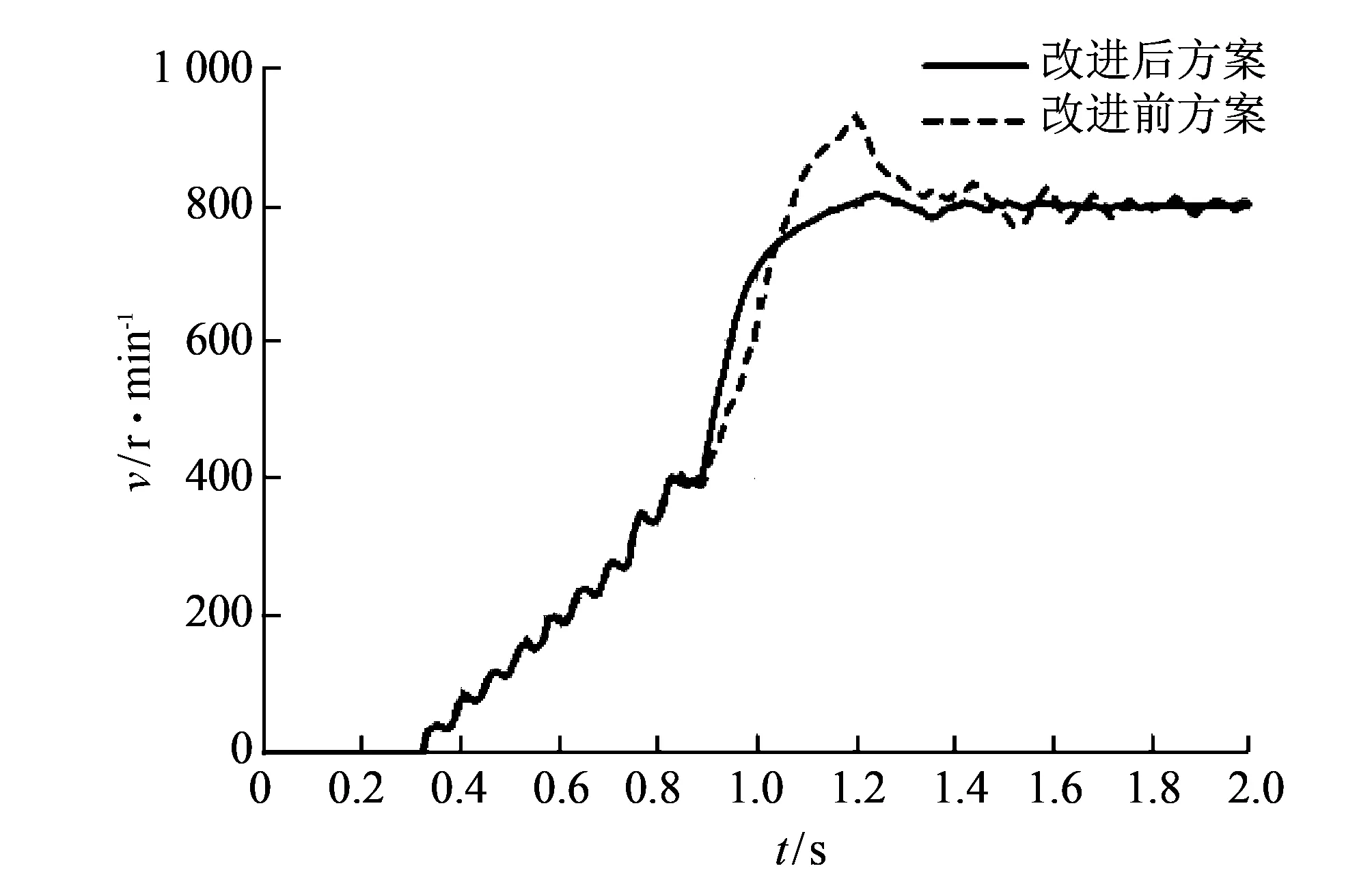
图 4 转速观测曲线Fig.4 Speed observation curve

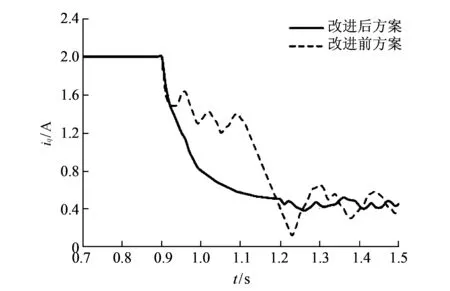
图 5 q轴电流波形Fig.5 q axis current waveform

实验结果表明： 采用变斜率电流幅值递减3段式启动方案能够实现带载快速启动. 预定位阶段能够精准定位， 不会出现过流现象， 在加速启动阶段能够抵抗负载扰动， 在状态切换阶段实现电流下降快速无冲击， 大大提高了PMSM系统的启动的可靠性与稳定性.

4 结 语

本文在对PMSM无位置传感器启动过程中进行模型机理分析的基础上， 研究了PMSM启动存在的问题， 提出基于电流幅值变斜率递减的改进3段式启动方法， 即采用电流闭环预定位法获得初始转子位置信息， 采用I/F速度开环、 电流闭环控制方法让电机转子平稳加速， 在状态转换过程中采用基于电流幅值变斜率递减的方法来使相位差值快速收敛， 使得PMSM电机能够按照预期的性能平滑启动.

无位置传感器PMSM的带载启动实验硬件平台采用意法半导体公司的中低端的32 b ARM微控制器STM32F103， 实验结果表明： 本文提出的改进3段式启动方法可靠性较高， 能保证PMSM带载情况下快速启动， 在整个启动过程中运行稳定， 无启动失败的现象产生.

参考文献：

[1] 朱军, 韩利利, 汪旭东. 永磁同步电机无位置传感器控制现状与发展趋势[J]. 微电机, 2013, 46(9)： 11-16.

Zhu Jun， Han Lili， Wang Xudong. Status and trends of sensorless control algorithm for PMSM[J]. Micromotors， 2013, 46(9)： 11-16. (in Chinese)

[2] 王萌， 杨家强， 张翔， 等. 一种表贴式永磁同步电机电流矢量闭环I/f控制方法[J]. 中国电机工程学报， 2015， 35(10)： 2513-2521.

Wang Meng， Yang Jiaqiang， Zhang Xiang， et al. An I/f control method with closed-loop regulation of current vector for surface permanent magnet synchronous motor drives[J]．Proceedings of the CSEE， 2015， 35(10)： 2513-2521. (in Chinese)

[3] 金光哲， 徐殿国， 高强， 等. 高频注入电压预估同步电机转子位置检测方法[J]. 中国电机工程学报， 2014， 34(9)： 1376-1383．

Jin Guangzhe， Xu Dianguo， Gao Qiang， et al. Synchronous motor rotor position detection method based on high-frequency injection voltage prediction[J]. Proceedings of the CSEE， 2014， 34(9)： 1376-1383. (in Chinese)

[4] 王高林， 杨荣峰， 李刚， 等. 基于高频信号注入的 IPMSM 无位置传感器控制策略[J]. 电工技术学报， 2012, 27(11)： 62-68.

Wang Gaolin， Yang Rongfeng， Li Gang， et al. Position sensorless control strategy of IPMSM based on high frequency signal injection[J]. Transactions of China Electrotechnical Society， 2012， 27(11)： 62-68. (in Chinese)

[5] 林东， 彭惠. 永磁同步电机开环V/F稳定控制方法[J]. 机电工程技术， 2012(10)： 33-35， 52.

Lin Dong， Peng Hui. A stable open-loop V/F control method for PMSM[J]. Mechanical and Electrical Engineering Technology， 2012(10)： 33-35， 52. (in Chinese)

[6] 陈卫兵， 宗蔚， 张凯泉， 等. 基于龙伯格观测器的内埋式永磁同步电机无位置控制算法 [J]. 湖南工业大学学报， 2016， 30(2)： 21-25.

Chen Weibing， Zong Wei， Zhang Kaiquan， et al. A sensorless control algorithm for interior permanent magnet synchronous motor based on luenberger observer[J]. Journal of Hunan University of Technology， 2016， 30(2)： 21-25. (in Chinese)

[7] 王子辉， 叶云岳. 反电势算法的永磁同步电机无位置传感器自启动过程[J]. 电机与控制学报， 2011， 15(10)： 36-42.

Wang Zihui， Ye Yunyue. Research on self-startup states process of back-EMF based sensorless vector control of PMSM[J]. Electric Machines and Control， 2011， 15(10)： 36-42. (in Chinese)

[8] Yoon Y D, Sul S K, Morimoto S, et al. Highbandwidth sensorless algorithm for AC machines based on square-wave-type voltage injection[J].IEEE Transactions on Industry Applications, 2011,47(3)： 1361-1370.

[9] 李彪, 李黎川. 基于高性能磁链算法的永磁同步电动机无位置传感器控制[J]. 电工技术学报, 2016, 31(11)： 59-67.

Li Biao， Li Lichuan. Position sensorless control of permanent magnet synchronous motor based on high performance flux EST[J]. Transactions of China Electrotechnical Society, 2016, 31(11)： 59-67. (in Chinese)

[10] 王子辉， 叶云岳. 反电势算法的永磁同步电机无位置传感器自启动过程[J].电机与控制学报， 2011， 15(10)： 36-42.

Wang Zihui， Ye Yunyue. Research on self-startup states process of back-EMF based sensorless vector control of PMSM[J]. Electric machines and control， 2011， 15(10)： 36-42. (in Chinese)

[11] 邓建国， 蔡亚辉， 黄守道， 等. 压缩机用永磁同步电机无传感器全速度运行策略研究 [J]. 中国机械工程, 2016, 27(6)： 767-771.

Deng Jianguo， Cai Yahui， Huang Shoudao， et al. Study on sensorless control strategy of PMSM for compressor at full speed range[J]. Chinese Journal of Mechanical Engineering， 2016， 27(6)： 767-771. (in Chinese)

[12] 刘海东, 周波, 郭鸿浩, 等. 脉振高频信号注入法误差分析[J]. 电工技术学报, 2015, 30(6)： 38-44.

Liu Haidong, Zhou Bo, Guo Honghao, et al. Error analysis of high frequency pulsating signal injection method[J]. Transactions of China Electrotechnical Society， 2015， 30(6)： 38-44. (in Chinese)

[13] Paulus D, Landsmann P, Kennel R. Sensorless field oriented control for permanent magnet synchronous machines with an arbitrary injection scheme and direct angle calculation[C]. Sensorless Control for Electrical Drives. IEEE, 2011： 41-46.

[14] Qiao Z, Shi T, Wang Y, et al. New sliding-mode observer for position sensorless control of permanent-magnet synchronous motor[J]. Industrial Electronics, IEEE Transactions on, 2013, 60(2)： 710-719.