Fock型空间中指数函数系的循环性与完备性
2018-06-19李夌,杜磊
李 夌, 杜 磊
(昆明理工大学 理学院, 云南 昆明 650093)
随着近年来分析学的发展和创新,概率理论与函数论结合的方法被越来越多的人应用。指数函数系的完备性问题也得到了更好的发展[1-2],其结果也被广泛应用。
在文献和中,令α(r)为一个定义在R上的非负连续函数,并且满足
(1)
那么与α有关的Fock空间Fα,p(1 其中dm2(z)记为Lebesgu面积测度,C为整个复平面。 如果f在Fα,p中满足 CloseL({znf,n≥0})=Fα,p, 就称f在Fα,p中是循环的。其中L是E的线性闭包[3-4]。 在文献中,Phragm⊇n-Lindelöf的论点表明在一定条件下如果多项式倍数pnf收敛到Fα,p中的一个元素,那么多项式不能足够大到逼近Fα,p中的每一个元素,其中f∈Fα,p,pn是多项式。由文献和,我们可以考虑指数函数系{eλz}(λ>0)在Fα,p(1 在这篇文章中将准解析的方法作为证明的基础,讨论函数系在右半平面是否解析[6],进而是否完备。这是和文献和完全不同的方法。同时在这里也会考虑在Fα,p(1 CloseL({znif,ni-ni-1≥1,ni∈N})=Fα,p。 最后,通过文献,再结合使用文献和中的Carleman公式来研究指数函数系{eλnz}(λn∈C)和缺项多项式{zni}在Fα,p(1 为了更方便的介绍我们的结论,先对一些必要的术语进行说明。 定义1[10]给定一个区间I⊂R和一个数列Mn>0,若C和ρ与f有关,且满足 |f(n)(x)|≤CpnMn,x∈I;n=1,2,…, 我们就说f在I上无穷可微,属于ΨI(Mn)类。 定义2[10]一个ΨI(Mn)类被称为准解析的,若任给一个x0∈I,仅有唯一的f∈ΨI(Mn)满足 fn(x0)=0,n=1,2,…, 则有f(x)≡0,x∈I。 引理1[10]如果 在以下的证明中,用A表示正常数,它在每次出现时可能不同。 引理2 若f(x)在任意区间I⊂R是无限可微的,且满足 |f(n)(x)|≤AK(n),n=0,1,2,3,…, (2) 其中K(n)是一个关于n的递增函数。那么就存在一个函数g(z)在右半平面C+={x=Rz>0,z=x+iy}解析,且满足 (3) 和 |g(z)|≤Ae2π|y|+K(x+1)。 (4) 证明不失一般性,我们可以假设[0,1]⊂I和b=1。定义 其中 那么由Taylor定理有 这说明存在一个函数g(z)在x>0的右半平面解析,所以对于在带形区域n 因此式(3)也是满足g(z)的。另外从 和式(2)及K(n)的增长性,可以得到当x>0时式(4)成立。 引理3[11]令β(x)为一个在R上满足式(1)的非负凸函数,假定 β*(t)=sup{xt-β(x):x∈R},t∈R 是函数β(x)的Young变换[12]。再假设λ(r)是一个在[0,+∞)上的增函数,且满足 λ(R)-λ(r)≤A(logR-logr+1)(R>r>1), 那么存在一个在C+上的非零解析函数f(z),满足 |f(z)|≤Aexp{Ax+β(x)-xλ(|z|)},z=x+iy∈C+, 使得当且仅当存在a∈R时, (5) 成立。 定理1 如果α(|z|)(|z|=r)满足式(1),α*(t)在任意有限区间I⊂R上有界,其中 α*(t)=sup{t|z|-α(|z|):t∈R+}, (6) 是Legendre变换或者是文献中α(|z|)(|z|=r)的Young对偶函数。同时如果 (7) 其中, α*(n)=sup{nlog|z|-α(|z|)}, (8) 那么对于任意的λ>0,函数eλz在Fα,p(1 证明如果对于一些λ>0,函数系{zneλz}在Fα,p(1 (9) |P(z)| ≤e-α*(|z|+N+1) 和Fubini定理及Morera定理,可以得到P(z)在x>0的右半平面解析。那么P(n)(λ)=0,n=0,1,2,…,另外,对于x>0有 因此,选择适当的A使得A>p2,A>q,可以得到 因为α*(x)在任意有限区间上有界,我们有 (10) 在任意有限区间I⊂R都成立。当λ>0时,可以选取适当的有限区间I⊂R满足λ∈I。因此若P(n)(λ)=0,n=0,1,2,3,…,和式(9)、(10)成立,可以得到在I上P(x)≡0。再根据P(z)的解析性,我们可以得到P(z)≡0,所以L≡0,这与L是非零函数矛盾。 定理2 令 (11) (12) 证明如果存在一些λ>0使得函数系{znieλz}在Fα,p(1 |P(z)| ≤eα*(|z|+N+1) 和Fubini定理及Morera定理,我们可以得到P(z)在x>0的右半平面解析。P(ni)(λ)=0,n=0,1,2,3,…,另外,对于x>0我们有 根据定理1的证明,我们有 因为α*(x)在任意有限区间上有界,我们可以得到在任意有限区间I⊂R上有 (13) 当λ>0时,我们可以找到一些有限区间I⊂R满足λ∈I。因此,若P(ni)(λ)=0,n=0,1,2,3,…,再根据引理2可知存在一个函数|g(z)|在x>0的右半平面解析,并且满足g(ni)=0和 |g(z)| ≤Ae2πy+α*Ax。 (14) 定义 其中 是文献中的Fuchs乘积。在这里已知 |G(z)| ≥exλ(r)-Ax,x≥0,z∈ΩΛ, (15) |g1(z)| ≤AeAx+α*Ax+2πx2-xλ(r), 也就是说 |g1(z)| ≤AeAx+β(x)-xλ(r) (16) 是成立的,其中β(x)如式(11)所定义。再根据式(12)和引理3,可以得到结论g1(z)≡0。因此g(z)≡0,进而有L≡0,这与L是非零函数矛盾。 定理3 若α(|z|)(|z|=r)满足式(1),α*(|z|)是递增的,而且对于某些Δ={z:Θ1 (17) 其中 则函数系{eλnz}在Fα,p(1 证明若函数系{eλnz}在Fα,p(1 |P(z)| ≤eα*(|z|+N+1), (18) 和Fubini定理及Morera定理,可以得到P(z)是一个整函数。对于Δ={z:Θ1 F(z)=P(zeiΘ0), 其中Θ0是常数且满足 类似文献[8-9],对在x>0右半平面的F(z)应用Carleman公式,不失一般性,可以假设|λn|>1,则下式 成立,其中d(1,r)是一个关于r的函数,并且当r→+∞时,d(1,r)趋向于一个常数。由α*(|z|)的增长性和式(18)可以得到 这与式(17)矛盾。 定理4 若α(|z|)(|z|=r)满足式(1),并且 (19) 其中 ni是不同的正整数,则缺项多项式{zni}在Fα,p(1 证明若缺项多项式{zni}在Fα,p(1 那么可以得到 因此, |P(z)| ≤Aeα*Ax, (20) 其中d(1,r)是一个关于r的函数,并且当r→+∞时,d(1,r)趋向于一个常数。由式(18)可以得到 这与式(19)矛盾。 1998年,A.A.Borichev和Bernard Beauzamy研究了在Fock型空间中函数的循环性条件,也研究了一些多项式的循环性和完备性。2010年,杨向东、易才凤两位教授讨论了在推广的Bergman-Fock空间中一种随机指数系的完备性,还对实轴上的加权Banach空间讨论了类似的问题。本文则是在Fock型空间中对所提出的几种指数函数系与缺项多项式的循环性和完备性同时进行了讨论。该研究是对Fock型空间的一些性质进行了补充和完善,也为相关问题的研究提供了新的思路和方法。 [ 参 考 文 献 ] [1] 杨向东,易才凤.Fock型空间中随机指数函数系的完备性.数学物理学报,2010,30(2):411-416. [2]柯思宇.指数系与随机指数系的完备性.北京:北京师范大学,2010:49-55. [3]BORICHEV A A.Estimates from below and cyclicity in Bergman-type spaces.Imm International Mathematics Research Notices,1996(12):603-611. [4]BEAUZAMY B.Introduction to Operator Theory and Invariant Subspaces.Amsterdam:Elsevier Science Publishers,1988:148-152. [5]BORICHEV A A.The polynomial approximation property in Fock-type spaces.Mathmatica Scandinavica,1998,82(2):256-264. [6]杨向东,邓冠铁.半平面中解析函数的积分表示及在逼近中的应用.数学物理学报,2008,28A(6):1242-1250. [7]DENG G T.Incompleteness and closure of a linear span of exponential system in a weighted Banach space.Journal of Approximation Theory,2003,125:1-9. [8]BOAS R P.Entire Functions.New York:Academic Press Inc,1954:351-362. [9]LEVIN B Y.Lectures on Entire Functions.Providence:American Mathematical Society,1996:196-223. [10] KOOSIS P.The Logarithmic Integral,Vol. I.Cambridge:Cambridge University Press,1988:15-77. [11] MALLIAVIN P.Sur quelques procedes d’extrapolation.Acta Math,1995,83:179-255. [12] ROCKAFELLAR R.Convex Analysis.Princeton:Princeton University Press,1970.1 一些定义及引理
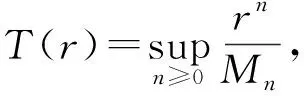
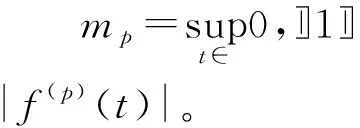
2 定理及证明





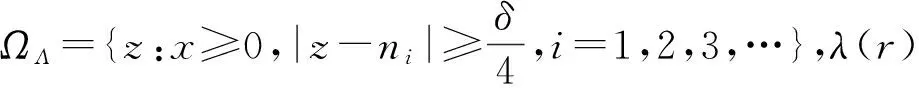



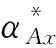
3 结束语
