以汽车电路为例浅析电路常用的3种分析方法
2018-06-18李佳倩
李佳倩
苏州工业园区职业技术学院 江苏省苏州市 215123
1 引言

图1 汽车发电机、蓄电池与用电电路
对于同一电路,我们可以用不同的电路分析方法对其分析求解,但每种电路方法都有适用范围,也就是说根据电路的特点我们可以选择合适的求解方法,下面以汽车电路为例如图1,分别用基尔霍夫分析法、电源等效变换法和叠加定理对其进行求解,并总结出每种方法适用的范围。
2 基尔霍夫分析法
图1是某汽车在某一工况下的等效电路图,已知汽车发动机的直流电动势E1=14V,内阻R1=0.15Ω;蓄电池的电动势E2=12V,内阻R2=0.1Ω。
(1)当负载是小负荷时,负载等效电阻R3=2.5Ω,求各支路电流。
(2)当负载是大负荷时,负载等效电阻R3=0.5Ω,求各支路电流。
根据基尔霍夫电流定律

方程(1)(2),只有一个是独立的。一般情况,具有N个结点的电路,只能列出N-1个独立的电流方程。
根据基尔霍夫电流定律

方程(3)(4)(5)只有两个是独立的,方程是否独立与选择的回路有关,在选择独立方程时,不要选择被包含的回路。一般情况,独立方程的个数等于网孔数。
将已知量代入(1)(3)(5),可得I1=10A,I2=-5A,I3=5A
I2=-5A,说明I2的方向与标定方向相反,发电机在向负载供电的同时还在向蓄电池充电,充电电流为5A。
(2)当负载是大负荷时,负载等效电阻R3=0.5Ω,依然用上述方法求解,可得
I1=17.143A,I2=5.714A,I3=22.857A
从表1可以看出,树木受害的情况和分布地点有一定的关系,火车站附近及国道两边过往车辆频繁,为害虫侵入提供了条件,单株林木有害虫3—14个,平均11个,国道边,单株林木有害虫2—12个,平均为8个,农田林网单株林木有害虫2—7个,平均为5个。由此看出,火车站附近黄斑星天牛危害严重,109国道边中等,农田林网危害比较轻。
I2=5.714A为正值,与标定方向相同,说明蓄电池向负载供电,也就是说发电机和蓄电池同时向负载供电。
3 电源等效变换法
用电源等效变换法来求解图1电路,将图1简化为图2,汽车发电机的直流电动势视为电压源US1=14V,内阻R1=0.15Ω;蓄电池的电动势视为电压源US2=12V,内阻R2=0.1Ω;负载电阻R3=2.5Ω,求各支路电流。
解:先将图2中的两个电压源分别等效为电流源,如图3所示,再将IS1和IS2、R1与R2分别合并,化成一个简单电路,如图4所示,根据电压源与电流源的等效变换条件,可得


图2

图3

图4
IS1与IS2合并得

R1与R2合并得

由图4可以看出,R12与R3是并联电路,可得
对于同一电路,我们用电源等效变换分析法和基尔霍夫分析法求出的结果是一样的,I3的电流大小和方向是一样的,对于I1和I2不再赘述,计算方法和I3相同。
4 叠加原理法
用叠加原理的方法求解图1的电路,如图5所示,将汽车直流发电机视为电压源US1=14V,内阻R1=0.15Ω;蓄电池的电动势视为电压源US2=12V,内阻R2=0.1Ω;负载电阻R3=2.5Ω,求I3。
解:US1单独作用时,将US2短接视为零,如图6所示:
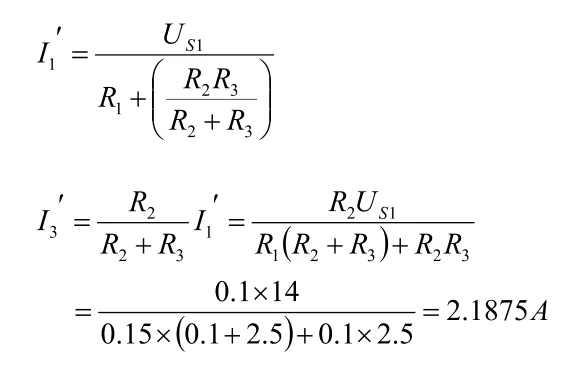
US2单独作用时,将US1短接视为零,如图7所示:


图5

图6

图7

当US1和US2共同作用时,根据叠加定理,可得

应用叠加定理对该电路进行分析,所得结果和基尔霍夫定理及电源等效变换结果完全相同,所以说对于这一电路三种方法都适合求解。
5 结语
电路分析方法有很多,基尔霍夫分析法、电源等效变换法、叠加定理、戴维南定理、诺顿定理等。本文对于同一个汽车电路,我们用三种电路分析方法分析该电路,并且得出的结果是一样。也就是说对于同一电路我们可以选择不同的分析方法,但是每一种方法也有其适用范围,不同的电路,我们可以选择最简单最适合的方法求解。基尔霍夫分析法不仅适用于直流电阻电路,也适用于交流电路及各种不同性质的元件所构成的电路,该方法适用于电路有3个支路以上求解支路电流;电源等效变换,电压源电流源都是实际电源的电路模型,它们之间可以互相等效变换,变换前后它们具有相同的外特性时可以等效变换,电源等效变换适用于有较多电源的电路;叠加原理是分析和计算线性电路的基本原理,它可以把一个复杂电路分解成几个简单电路来计算。叠加原理只适用于线性电路的电压、电流计算,不能用于功率计算。叠加定理适用于电路中存在多个电源(电压源和电流源)。
