顶部空隙存在时的“流动泄露”模型验证

杨 颖，刘 宁，黄 迎

（重庆大学动力工程学院，重庆 400044）

现代科技的发展，促使电子器件向着微型化、高性能的方向发展，这导致电子器件的热流密度越来越高，换热压力越来越大。水冷作为一种高效的散热方式，近年来越来越被重视，而平板肋片则是换热器中使用最为广泛的模型之一，因此对平板肋片的结构，如肋片间距，肋片高度，肋片厚度等进行优化以达到最佳的换热性能一直是研究者们的重点，但对平板肋片中顶部空隙的研究则非常少，且大多数都是以空气为工质展开的研究。所谓顶部空隙，即肋片顶端与水冷通道盖板之间的间隙。

E.M.Sparrow［1］最早等利用数值方法研究了当流动为层流时，矩形肋片换热器中存在顶部空隙时的换热表现，他们发现当存在顶部空隙时，肋片顶端的换热强度最高，而没有间隙时，肋片中间部分的换热最强。当顶部空隙较大时，特别是肋间距较小时，肋片的大部分位置换热强度几乎为0。他们也实验研究了湍流时的顶部空隙影响［2］，实验结果显示空隙的存在会降低换热系数，而存在空隙与不存在空隙时的充分发展换热系数之比仅与空隙与肋片高度之比有关。

夏国栋等［3］针对微针肋顶端间隙对流动和传热的影响，利用计算流体力学软件进行了三维数值模拟。通过定义无量纲间隙比t=Cg/D，其中Cg为顶端空隙高度，D为针肋直径，模拟结果发现，流动为层流时，存在着最优无量纲间隙比使热沉的热阻最小：定流量与定泵功率下的最优无量纲间隙比分别为0.3与0.5。M.Reyes［4］等人通过实验研究了以水为工质的微通道换热器的换热与压降，发现顶部空隙的存在能很大程度上减小换热器的压力损失，而对换热效率的影响却相对较小。

C.Liang［5］等人也通过实验研究了顶部空隙对微通道换热器的影响，其结果显示当工质为水时的研究成果能很好的应用到非牛顿流体工质上。Han-Taw Chen［6］等人结合CFD模拟、实验以及逆解法，对风道中的平板肋片的换热与压降表现进行了研究，结果表明在模拟过程中，流动模型的选择，近壁的处理以及软件版本都对结果有着很大的影响。

Krishna Kota 等［7-8］通过理论分析介绍了以空气为介质的平板肋片热沉中存在旁流时的换热与压降性能，为了简化理论模型，文献忽略了肋片通道与旁流交界面的空气质量交换，并将空气假设为无粘、不可压流体。理论分析结果发现：当旁流存在时，旁流通道中的低流阻会导致更多的工质从旁通流过而不与肋片进行热交换，因此增加肋片的紧凑度，或者增加肋间通道的沿程阻力系数均会导致旁流对平板肋片热沉换热与压降性能的影响加大。

为了预测顶部空隙存在时肋间的平均流速，学者们［9-11］通过实验或模拟研究的方式提出了各自的数学模型，且模型均在特定的条件下与实验或数值结果吻合。有两种物理模型被广泛研究，一种是独立模型，即将空隙与肋间通道看做相互独立的流动通道，另一种则是“流动泄露”模型，即在空隙与肋间通道之间存在着质量交换。本研究的目的是结合模拟与实验，通过研究顶部空隙的存在对平板肋片换热性能的影响，来验证“流动泄露”模型的合理性。

1 实验系统与实验过程

1.1 实验台构造

实验装置如图1，整个实验系统主要包括四个部分：测试区、流量计、水循环功能部件以及数据测量与采集系统。根据实验期间的当地平均温度，入口水温选择为26.3 ℃，使用一台恒温水箱来保证入口水温的恒定。在实验过程中，水箱中的水被泵驱动流经测试区，与测试区中的平板肋片发生对流热交换来带走加热片提供的热量，最后流经流量计回到水箱，水的体积流量由阀门控制为固定值，并通过流量计直接显示。两个微型压力传感器分别放置在测试区的进出口来测量整个测试区的压降。

图1 实验装置图

1.2 测试区构造

测试区构成如图2，主要由5个部件组成。陶瓷加热片作为热源，被放置在肋片底部提供恒定的热流密度，它的尺寸与肋片底板一致，为50 mm* 50 mm。加热片实际的加热功率可以通过直流电源上显示的电压与电流值通过欧姆定理得出，且加热功率可以通过改变直流电源的电压值来非常方便的改变。肋片的材料选用导热系数为160 W/m2的6061铝合金，并通过整体加工的方式加工，这样可以消除接触热阻的影响。在肋片底部与加热片之间也涂有一定厚度的导热硅脂，来减少接触热阻。本实验共使用了15种不同结构的平板肋片，包括5种高度（10 mm，15 mm，20 mm，25 mm，30 mm）和3种肋间距（1 mm，2 mm，3 mm），每一种结构的肋片均研究了6个不同高度顶部空隙的影响（0 mm～5 mm）。为了区别不同结构的换热器，本文采用了一种较方便的编号，以10-3-2为例，10代表肋片高度，3代表肋间距，2代表顶部空隙高度。

图2 测试区构成图

除了加热片以及肋片外，整个测试区由亚克力板加工而成，图3中tip clearance板用来改变实验过程中的顶部空隙高度，当不放置此板时，肋片顶端与盖板之间的距离固定设计为5 mm，即此时的顶部空隙为5 mm，当在盖板下粘上厚度为3 mm的此板时，顶部空隙被改变为2 mm，此板厚度为5 mm，时，此时无顶部空隙。

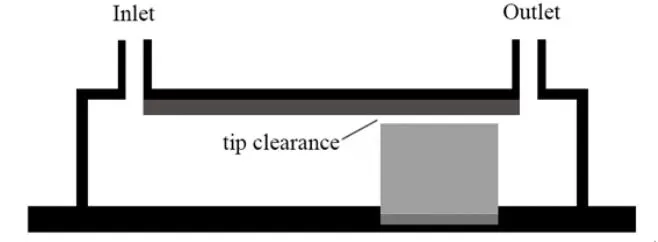
图3 测试区整体图

如图3所示，肋片左端设置有进口段以使进口流动均匀。两个热电偶被分别布置在测试区的进口与出口，测量进出口水温。而在肋片底板与加热片间布置了如图4所示的4个热电偶来测量平板肋片底板平均温度。在实验前，所有热电偶均使用二级标准温度计校核。

图4 热电偶位置

1.3 实验不确定性分析

实验过程中用到的T型热电偶的精度为±1 ℃，而实验过程中的最高温度为39 ℃，因此温度相对不确定性为2.56%。压力传感器的精度为5 pa，实验中的最大压力为105.42 pa，因此压力相对不确定性为4.7%。流量计的精度为6 L/h，整个实验过程的体积流量为94.05 L/h，因此其相对不确定性为6.38%。平板肋片的加工精度为0.1 mm，因此其尺寸的相对不确定性为2%。根据文献［12］可知，复合参数的不确定度可以表示为：

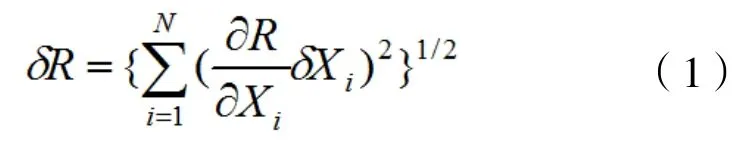
因此在整个实验过程中，Nu数与Re数的相对不确定度分别为13.4%和6.38%。

2 CFD模型

在散热器的设计与性能优化过程中，计算流体力学（CFD）软件有着实验无法比拟的时间优势与经济优势，因此正越来越广泛的被应用。

首先利用CFD软件对14组不同结构的模型进行模拟，将得到的结果与实验结果进行对比验证模拟结果的可靠性，随后对不方便进行实验的模型结构进行模拟研究。

图5为模拟过程中所用到的模型之一，因为整个模型区域是对称的，因此可将整个模型的一半作为计算域，这有利于减少计算时间，且与整体域的计算结果之间的误差仅为±0.2%［13］。在整个计算过程中，选用层流模型作为流动模型，因为与湍流模型得出的结果相比较，层流模型与实验结果的吻合度更高。为了与实验条件保持一致性，热源设置为体积热源。

图5 CFD对称模型

3 数据处理

为了研究顶部空隙对平板肋片换热性能的影响，实验数据与模拟计算数据按如下的过程进行处理：

考虑到肋片高度方向上的温度变化，在数据处理过程中引入肋片效率ηf，因此整体的对流换热量可以表示为

hm是模型平均对流换热系数，Ab和Afin分别为肋片底端板面以及肋片表面积。Ab=L（W-Nft），Afin=LNf（2Hf+t）·Tb为肋片底端板面平均温度，可以根据傅里叶导热定律计算得到：

Tbp为平板肋片与加热片接触处底板的平均温度，由4个T型热电偶直接测量得到。

流体平均温度Tm为测试区域进出口的平均水温，

由于亚克力板的导热系数与铝合金相比非常小，水箱的热损失量相比肋片的对流换热量非常小，可以忽略不计。因此在实验过程中，可以近似认为热源产生的热量全部由水与平板肋片的对流换热带走。

对一维问题，肋片的肋片效率可以表示为

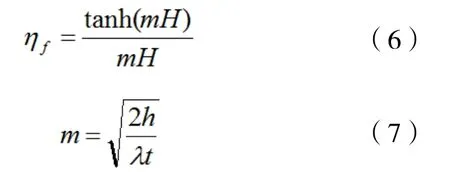
H的取值与模型的结构有关：当无顶部空隙时，H=Hf，而顶部空隙存在时

因为ηf的计算公式中包含了未知量hm，因此在整个计算过程中需要用到迭代法。首先将ηf取值为1，根据公式（2）计算得到hm，其次将得到的hm代入到公式（6）和（7）中得到一个新的ηf。重复上述过程，直到结果收敛，得到最终的ηf与hm。

结构整体热阻（TTR）描述了某一换热量下肋片底端板面与流体的温度差，因此是衡量换热器换热能力的重要参数之一。

Nu定义为为水的导热系数。Re定义为为水的动力粘度，在实验过程中平均水温为26.4 ℃，因此μ的取值为0.000 861 9 。

所有准则数均取无顶部空隙时的肋间通道水力直径为特征长度，即，其中Ac为肋间通道截面面积，Pc为截面湿周。

4 结果分析

4.1 模拟可靠性验证

图6通过对比实验与数值计算的TTR值来验证CFD模拟结果的可信度。图6a表示了肋片15-1 与15-3 在不同顶部空隙时的TTR值与无顶部空隙时的TTR值的比值，结果表明模拟结果与实验结果有着相同的变化趋势，即模型总热阻随着顶部空隙的增大而增大。其中肋片15-3的模拟与实验结果吻合度非常好。而对肋片15-1，两个结果存在着偏差（20%）。

图6 实验与模拟TTR值对比

图6b显示了模拟计算结果与实验结果中，不同结构参数的肋片在顶部空隙为5 mm与无顶部空隙下的TTR比值。可以发现实验结果与模拟结果的吻合度良好，最大的偏差（15%）出现在肋片10-3。

通过以上的对比可以发现，虽然实验与模拟结果存在着一些偏差，但整体结果是吻合的，考虑到肋片表面粗糙度的影响，以及实验测量的误差，因此在本文顶部空隙对换热影响的研究中，利用CFD软件计算的结果是可接受的。

4.2 “流动泄露”的验证

4.2.1 顶部空隙对换热性能的影响

图7与图8通过对比顶部空隙存在与不存在时的整体热阻，显示了顶部空隙的存在对换热器换热性能的影响：随着顶部空隙的增大，平板肋片换热器的换热性能也随之单调的减小。因为尽管当存在顶部空隙时，肋片顶端的面积参与换热增加了整体换热面积，但旁流导致的流量减少会大幅减小平均对流换热系数，最终导致肋片的整体温升增大，即换热能力减小。

从图7中还可以看出，当肋片高度固定时，肋间距越大，顶部空隙对平板换热的影响越小。因为肋片底板尺寸固定时，肋间距越大，意味着肋片数目越少，肋间的水流通道截面积也越大，因此对于固定的顶部空隙高度，增加的相对过流面积更小，对换热的影响也更小。而且当肋片数目越少时，通道中的流阻也越小，旁流量也越小。

图7 固定H与不同S下顶部空隙影响

图8比较了固定的肋间距情形下，不同高度的肋片的整体热阻随顶部空隙高度的变化，结果显示当顶部空隙高度与肋间距都固定时，肋片高度越小，顶部空隙的影响越明显，这个现象也可以用前面所描述的相对过流面积增加量来解释。

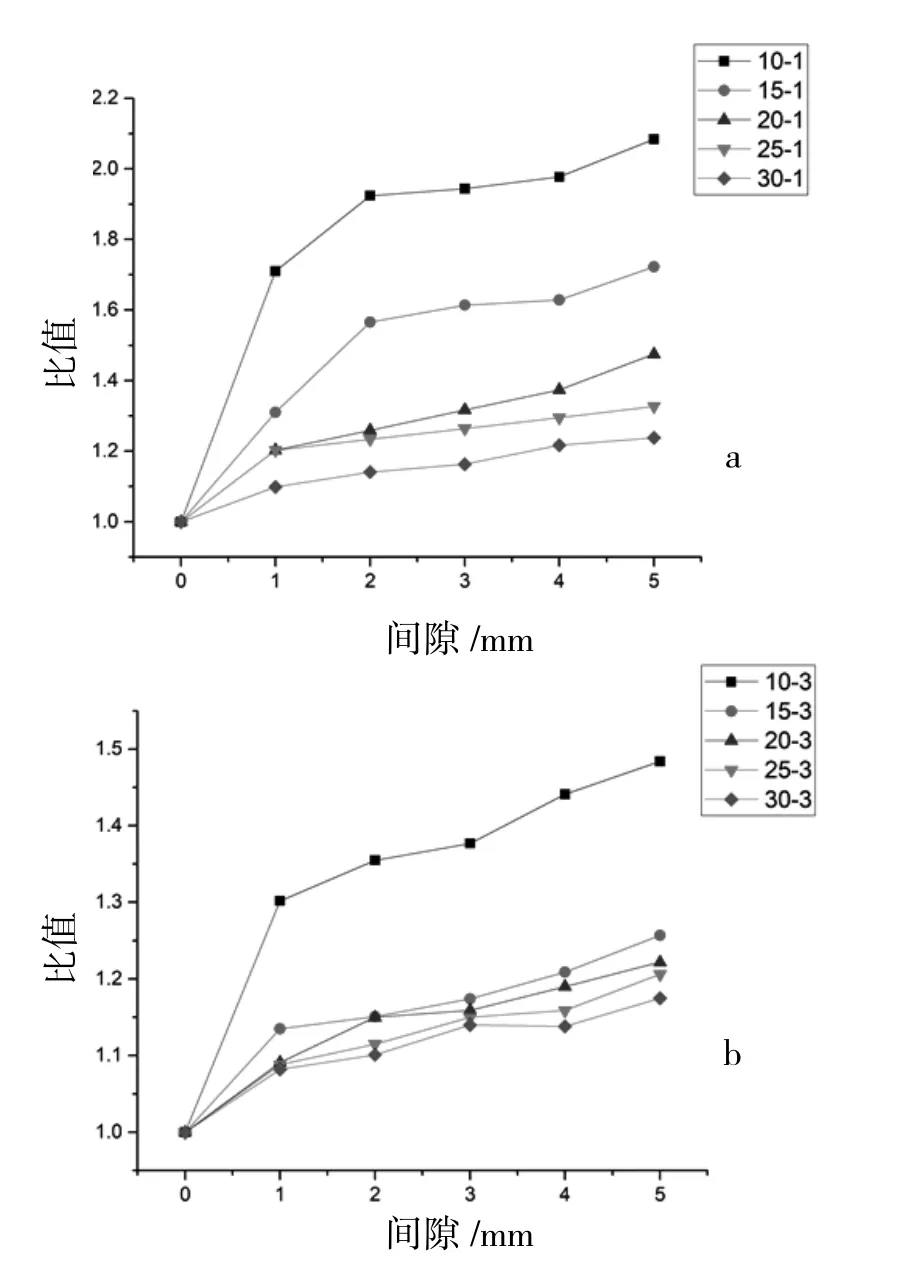
图8 固定S与不同H下顶部空隙影响

4.2.2 肋片温度分布

表1 与表2为模拟计算结果得到的肋片表面温度分布情况，其中ΔTHeight为肋片高度方向的温度变化，即肋片底部与顶端的温差；ΔTflow为肋片表面径向温度变化，即进出口肋片表面温差。

从表1中可以发现，当肋间距一定时，ΔTHeight随着肋片高度的增加而增加，而当平板肋片的尺寸，如肋间距与肋片高度等均固定时，ΔTHeight随顶部空气高度的改变非常小。这个现象可以用傅里叶导热定律解释：对于固定的肋片结构，肋片高度方向的温度变化越大，意味着通过热传导传递的热量越大；而对固定的导热量，肋片高度越高，则肋片底部与顶端的温差也越大，即ΔTHeight越大。这也可以解释另外一个现象：当肋片高度与顶部空隙高度固定时，当肋间距为3 mm时的ΔTHeight大于肋间距为1 mm的情况。因为总的传热量固定，因此肋间距越大，肋片数目越少，单片肋片的传热量也就越大，当肋片高度一定时，ΔTHeight也就越大。

表1 S=1 mm时的肋片温度分布

表2 S=3 mm时的肋片温度分布

对不同的肋片高度，当肋片顶部空隙为0时，肋片径向均存在温度变化，因此在本文的研究中，流动入口段的影响不可忽略。另外，当肋片高度与肋间距固定时，ΔTflow随着顶部空隙的增加而增大，且当S=1 mm时，这个变化对比S=3 mm的肋片更明显。因为当整体的换热量与平板肋片尺寸固定时，肋片径向温度变化越大，代表着流动方向的局部换热系数变化越大，而影响流动方向局部换热系数的因素有两个：流速以及入口效应。而当顶部空隙高度增加时，会减弱入口段的影响，因此ΔTflow随着顶部空隙高度的变化主要影响因素是径向流速的变化。这也能证明当顶部空隙存在时的“流动泄露”模型的合理性：当肋片顶端存在空隙时，因为空隙中的流阻较小，因此一部分流体会从肋片之间的通道流向顶部空隙，导致肋片之间流动方向的流速减小，顶部空隙越大，流向其中的流体占比越大。当肋片高度固定时，肋间距为3 mm时，流阻远小于肋间距为1 mm的情形，“流动泄露”在不同的顶部空隙高度下均非常小，因此不同空隙高度下的ΔTflow差别不大，但肋间距为1 mm时却与之刚好相反。

5 关联式

Elshafei［14］在一维换热的假设下，给出了Nu数与雷诺数Re以及其他结构参数包括肋片顶部空隙高度直接的经验关联式

这个关联式的验证范围是3 000＜Re＜38 000，而本文的研究范围为层流，且需考虑入口段效应的影响，因此依据层流换热Sieder-Tate 关联式对式（9）进行了一些修正，修正后的关联式为：

为了验证修正后的关联式适用性，图9 将式（10）计算得到的Num与模拟计算得到的Nu进行对比，发现当S=3 mm时，Num/Nu值均接近于1，即模拟结果与关联式结果吻合；当S=1时，顶部空隙为0时，两者的结果也是吻合的，但是当存在顶部空隙时，关联式计算结果与模拟计算结果存在着较大的偏差，且偏差随着顶部空隙的高度增大而增大。

图9 模拟与关联式结果对比

这个结果能进一步证明“流动泄露”模型，当顶部空隙为0，或肋间距为3 mm时，换热器流阻非常小，因此肋片间的流体流向顶部空隙的部分非常小，因此关联式能比较准确的计算换热器的换热效率，而当肋间距为1 mm，且存在顶部空隙时，此时的“流动泄露”较大，使得平板肋片内的流动变得非常复杂难以预测。

6 结论

本文结合实验与模拟的方式，研究了平板肋片顶部空隙对其流动与换热的影响，得出以下结论：1）顶部空隙的存在会减小平板肋片换热器的换热效率；2）对肋片表面温度分布的分析验证了顶部空隙存在时，“流动泄露”模型的合理性，因此在研究换热器中流体流动时，不能忽略“流动泄露”的影响；3）低Re条件下，存在顶部空隙时的Nu数计算经验关联式，它适用于流阻较小的情形，在流阻较大时与实际结果存在偏差，因此更准确，适用条件更广的关联式需要后续更深入的研究。

［1］ SPARROW E M，BALIGA B R，PATANKAR S V.Forced Convection Heat Transfer from a Shrouded Fin Array with and without Tip Clearance［J］.Journal of Heat Transfer，1978，100（4）：572.

［2］ SPARROW E M，KADLE D S.Effect of Tip-to-Shroud Clearance on Turbulent Heat Transfer From a Shrouded，Longitudinal Fin Array［J］.Journal of Heat Transfer，1986，108（3）：519-524.

［3］ 夏国栋，周利军，周明正，等.肋端间隙对微针肋热沉流体流动和传热的影响［J］.工程热物理学报，2011，32（12）：2086-2089..

［4］ REYES M，ARIAS J R，VELAZQUEz A，et al.Experimental study of heat transfer and pressure drop in micro-channel based heat sinks with tip clearance［J］.Applied Thermal Engineering，2011，31（5）：887-893.

［5］ LIANG C，ARIAS J R，VELAZQUEZ A.Tip Clearance Effects on Microchannel-Based Heat Sink with Polymeric Fluid［J］.Journal of Thermophysics & Heat Transfer，2015，30（2）：1-9.

［6］ CHEN H T，TSENG H C，JHU S W，et al.Numerical and experimental study of mixed convection heat transfer and fluid flow characteristics of plate-fin heat sinks［J］.International Journal of Heat & Mass Transfer，2017，111：1050-1062.

［7］ KOTA K，AWAD M M.Understanding the impact of Flow Bypass on the overall pressure drop of air cooled heat sinks［J］.IMECE，2014：826-832.

［8］ KOTA K，AWAD M M.Understanding the Impact of Flow Bypass on the Thermal Performance of Air Cooled Heat Sinks［C］.Thermal and Thermomechanical Phenomena in Electronic Systems.IEEE，2014：826-832.

［9］ HOSSAIN R，CULHAM J R，YOVANOVICH M M.Influence of bypass on flow through plate fin heat sinks［C］.Annual IEEE Semiconductor Thermal Measurement & Management Symposium，2007，220-227.

［10］ KEISUKE，HORIUCHI，ATSUO，et al.Experimental Verification of Model for Liquid-Cooled Staggered Pin Fin Heat Sinks with Top Bypass Flow［J］.能源与动力工程：英文版，2013（8）：1487-1495.

［11］ DOGRUOZ M B，ORTEGA A，WESTPHAL R V.A model for flow bypass and tip leakage in pin fin heat sinks［J］.Journal of Electronic Packaging，2006，128（1）：53-60.

［12］ MOFFAT R J.Describing the Uncertainties in Experimental Results［J］.Experimental Thermal & Fluid Science，1988，1：3-17.

［13］ PRSTIC S，IYENGAR M， BAR-COHEN A.Bypass effect in high performance heat sinks［C］.Proceedings of the International Thermal Science Seminar Bled，2008，1：255-262.

［14］ ELSHAFEI E A M.Effect of flow bypass on the performance of a shrouded longitudinal fin array［J］.Applied Thermal Engineering，2011，27（13）：2233-2242.