一个奇异值不等式的推广

刘俊同，刘 越

（1. 阜阳师范学院 数学与统计学院，安徽 阜阳 236041；2. 阜南县 第五小学，安徽 阜南 236000）

奇异值不等式和奇异值分解是矩阵理论的一个重要研究领域，在科学计算、优化问题、最佳逼近等实际应用中有着重要应用。关于矩阵酉不变范数不等式和奇异值不等式问题是矩阵不等式的研究热点之一，近年来受到国内外专家学者的广泛关注[1-10]。Zou证明了如下奇异值不等式[5]

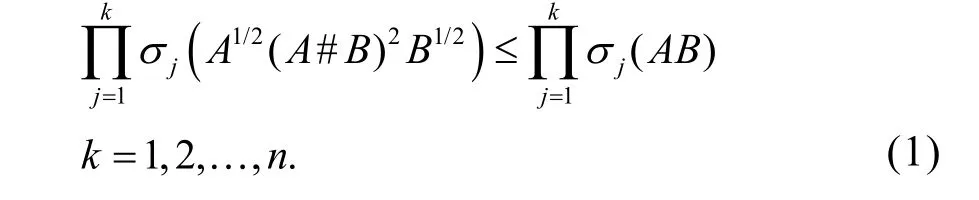
对n阶半正定矩阵A和B成立。

本文尝试对奇异值不等式(1)进行推广，我们将证明如下奇异值不等式

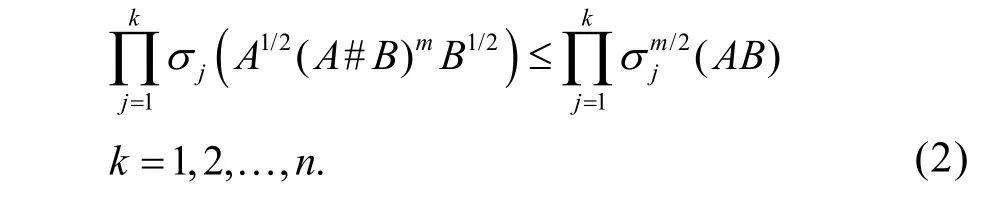
对n阶半正定矩阵A和B成立。

1 预备知识

为了叙述方便，对符号作如下约定：Mn表示复数域上n× n矩阵的集合，A*表示A的共轭转置矩阵，A的奇异值记为

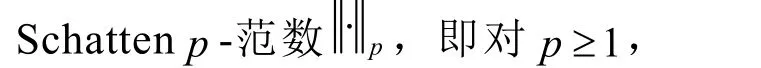
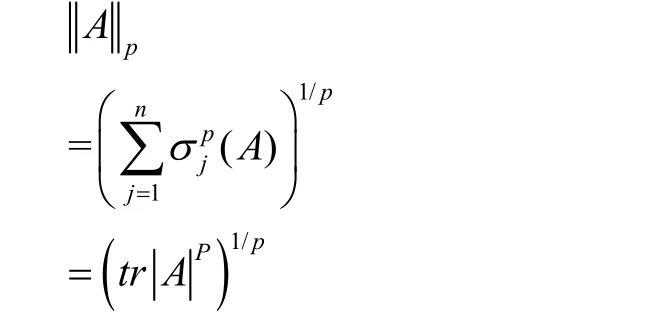
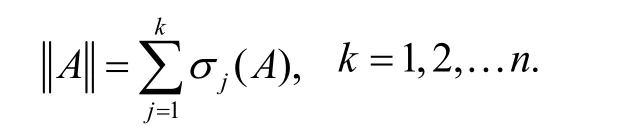
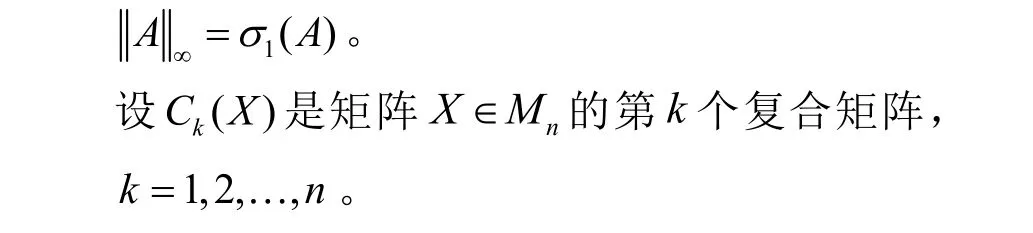
对于两个正定矩阵

通过矩阵函数的连续性，两个矩阵A与B的几何平均可以推广到对任意两个半正定矩阵。

为了证明奇异值不等式(2)，需要如下几个引理。其中引理1和引理2是矩阵分析的两个经典结果，而引理 3描述的是复合矩阵的两个重要性质。

引理 1[11,p94]设 ,n A B∈M，且矩阵A和B是半正定的，对任意的

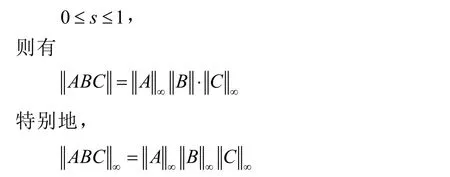
引理 2[11,eoremIX2.1]设A,B∈M，且矩阵An和B是半正定的，对任意的

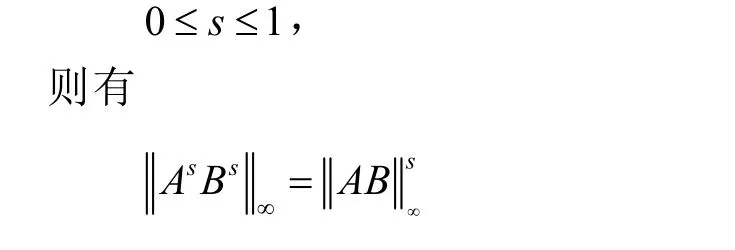
引理3[12,p123]设A,B∈M，则有

n

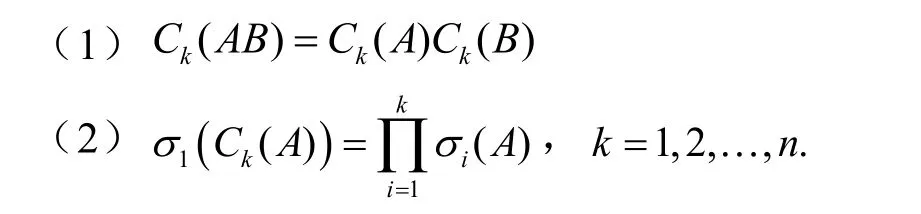
2 定理及证明

定理1设A,B∈Mn，且矩阵A和B是半正定的，则有

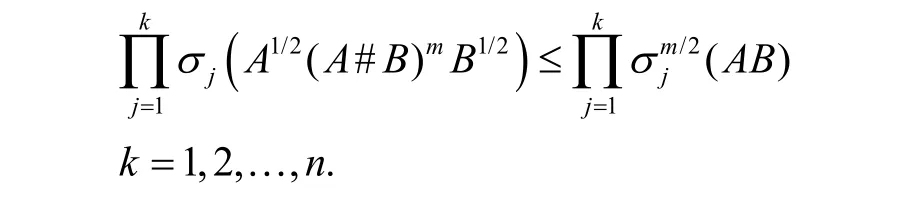
证明首先假定矩阵A和B是正定的，一般情形可以通过连续性论证证明。从文献可知

设Ck(X)是矩阵X∈Mn的第k个复合矩阵，

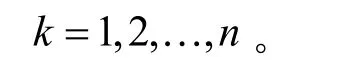
于是，有

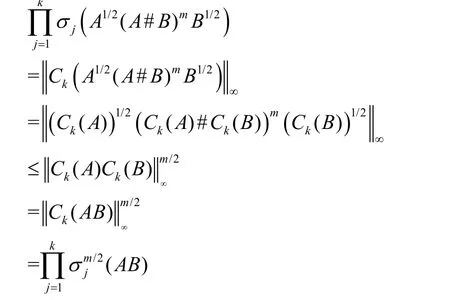
当m=2时，得到不等式(1)，即推论1。

推论1设A,B∈Mn，且矩阵A和B是半正定的，则有

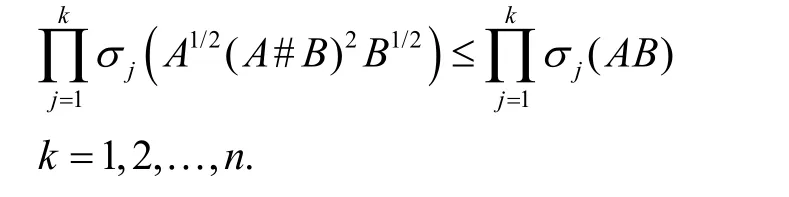
由于弱Log-majorization蕴含弱majorization，

通过推论1，有推论2。

推论2设 A, B ∈Mn，且矩阵A和B是半正定矩阵，则有

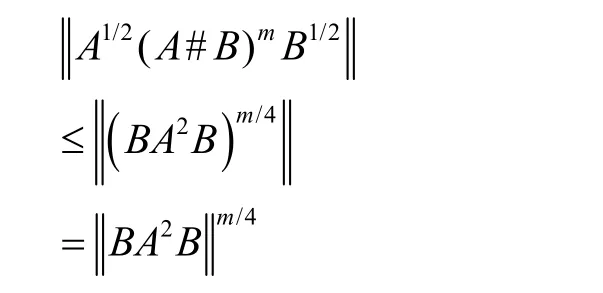
特别的，当m=2时，有推论3。

推论3设 A, B ∈Mn，且矩阵A和B是半正定矩阵，则有

[1] R. A. Horn, C. R. Johnson. Matrix Analysis[M].Cambridge： Cambridge University press, 1985： 279-372.

[2] R. A. Horn, C. R. Johnson. Topics in Matrix Analysis[M].Cambridge： Cambridge University press, 1991： 134-238.

[3] X. Zhan. Matrix inequalities[M]. Berlin： Spinger-Verlag,2002： 17-109.

[4] 王松桂,吴密霞,贾忠珍.矩阵不等式[M].北京：科学出版社,2006：222-288.

[5] L. Zou. A arithmetic-geometric mean inequality for singular values and its applications[J]. Linear. Algebra.Appl, 2017, 528： 25-32.

[6] 邹黎敏.矩阵的几个不等式[J].数学通报,2012,55(4)：715-720.

[7] 宫琴,任芳国.关于矩阵奇异值的不等式[J].纺织高校基础科学学报,2016,29(1)：1-7.

[8] Y. Tao. More results on singular inequalities of matrices[J]. Linear Algebra Appl, 2006, 416(2)： 724-729.

[9] 陶云星.关于矩阵酉不变范数和奇异值的两个问题[D].北京：北京师范大学,2005：1-38.

[10] A. Ilyas. Studies of singular value inequalities about matrix and inequalities of norms[D]. Chongqing：Chongqing University, 2014： 1-61.

[12] F. Zhang. Matrix theory： basic results and techniques[M]. New York： Springer-Verlag, 2012.

[11] R. Bhatia, Matrix Analysis[M]. GTM 169, New York：Springer-Verlag, 1997.