思考力、批判力和表达力:自主学习的核心动力——“平行四边形的面积”教学新思考

◇彭永新

在“适合的教育”视域下，应如何实施学生的自主学习？教师应具备“人”的视角，从学生的学出发，关注“教育的适切性”，即自主学习是否适合所有的孩子、是否适合他们的发展需要，学生是否具有必备的学习策略等。因此，教学中教师要努力创设“适合的环境”，做到因材施教、教学相长；为学生提供“适合的脚手架”，实现在“适合的教育”视域下学生自主学习意识的觉醒和能力的提升。于是，对于“平行四边形的面积”一课，我进行了如下的教学设计。

1.提出问题：星海小学有一个著名的四叶草农场，大家去过吗？现在我们去看看。

出示：颜阿姨用栅栏围了两块地，准备种植不同的蔬菜。（如图1）

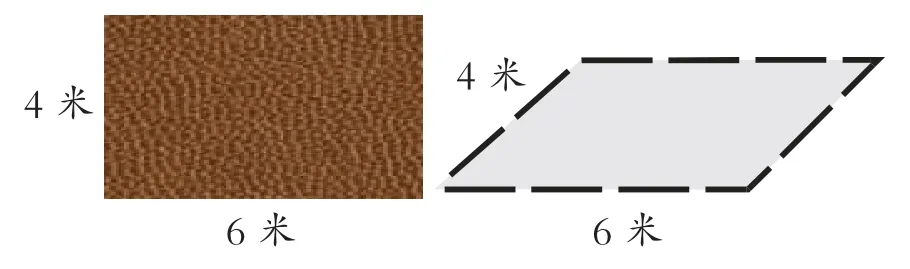
图1

提问：比一比，你能看出这两块地哪一块的面积大一些吗？（板书：面积）

（1）声音一：面积不相等，长方形面积大，平行四边形面积小。

提问：面积不一样大吗？为什么？（有人可能根据预习已经知道平行四边形面积计算不是看两条邻边的乘积，而是看底和高，明显地看出右边平行四边形的高要小一些）高在哪里？你能比画一下高的位置吗？（课件移动两个图形使其重合，如图2）这样的说法有没有道理呢？（让其他人发表看法质疑刚才的想法）

图2

引导：平行四边形的面积是不是用底乘高来计算，我们先不忙回答这个问题，我想还是回到刚才的问题上：请大家先观察一下这两个图形，重叠在一起的时候，各有一部分露出来，你们能不能通过剪剪拼拼，来证明平行四边形的面积确实比长方形小？

（2）声音二：面积相等。

提问：为什么？（估计有人会这样想：这两个图形的栅栏长度一样长——提示：可形状不一样啊！重合图形如图2）

引导学生提出平行四边形通过变形就能变成长方形（提问：怎么变成长方形？引发拉动框架想法），这时平行四边形（长方形）的面积只要用两条邻边相乘就可以了。

2.探究问题：现在老师给每人准备了这样的平行四边形和长方形，请四人一组讨论一下，怎样把平行四边形剪拼，就能比出大小来？

（学生小组讨论，并动手实践，教师巡视指导）

展示学生操作想法，重点提问：沿着哪条线剪？分成哪两块？怎么补？有没有不一样的剪法？并进行电脑演示。（沿着中间一条高操作，也能拼成）

师生一起探究面积变小的原因。请大家再次比一比：剪拼后变成一个什么图形？图形面积有没有改变？（板书：等积变形）这个长方形还是原来那个长方形吗？怎么小了一点呢？

在学生介绍后，教师引导观察：平行四边形经过割补后，它的一条边也就是现在这个长方形的宽，为什么变小了？（高比斜边短）

3.类推：通过刚才的研究，我们发现平行四边形可以通过等积变形，变成一个新的长方形。请说说看，下面的平行四边形（图略）分别与怎样的长方形面积一样大？

要求学生将课本后面的平行四边形纸片进行剪拼操作，并进行现场演示汇报，发现所有的平行四边形都能通过等积变形转化为相应的长方形。在此基础上再次进行观察讨论：

（1）剪拼后长方形的面积与平行四边形的面积相等吗？

（2）剪拼后长方形的长和宽与平行四边形的底和高有什么关系？

（3）根据长方形的面积公式，怎样求平行四边形的面积？

通过讨论推导出平行四边形面积计算公式。

4.练习：

（1）直接口算图形面积。（图略）

（2）选择列式。（题略）

（3）拓展：画两个等积平行四边形（画在格子图上）。

（4）回到四叶草农场：颜阿姨又用同样的栅栏围了一个平行四边形（如图3）。

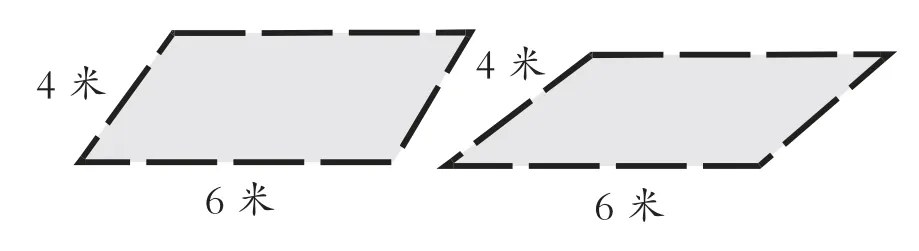
图3

比一比：这两个平行四边形，哪个面积大一些？为什么左边要高一些呢？谁能发现高的变化是因为什么的变化引起的？（角度）

显然，这个角度越大，平行四边形的面积就越大，角度越小，平行四边形的面积就越小。这就是说，平行四边形的面积不仅仅与两条邻边的长度有关系，还跟角度的大小有关。因此，我们计算平行四边形的面积还有一种新的算法“S＝a×b×？”，这个问号就是跟角度有关的一个量。这个知识，我们到初中再研究。