基于QMC-IPF-JPDA的多目标无源协同定位算法*

陈明淑，李 盛，赵 婧

（西京学院理学院，西安 710123）

0 引言

无源协同定位［1］指的是雷达本身不发射电磁波，借助非合作外辐射源（如手机通信基站，数字电视信号基站等［2］）发射的电磁波来检测跟踪目标。与传统的有源雷达［3］相比，无源协同定位系统具有反侦察、抗干扰、反隐身和防反辐射导弹等优点。除此之外，无源协同定位系统利用双、多基站的空间分布性大幅提高了系统对低空和隐身目标的探测性能，受到了国内外学者的广泛关注［1-2，4-5］。

由于无源协同定位系统中目标信号被杂波所淹没，并且同一时刻可能存在多个目标，如何利用无源协同定位系统实现多目标的检测与跟踪，成为亟待解决的关键问题之一。文献［6］提出一种基于粒子滤波概率数据关联的单目标检测跟踪方法，该方法利用跟踪门对回波进行预处理，筛选出有效回波，并利用粒子滤波对关联概率中的残差协方差阵进行修正，通过关联概率得到融合测量实现目标状态更新。文献［7］为解决杂波环境下多机动目标的数据关联难题，提出一种将粒子滤波器和联合概率数据关联相结合的数据关联算法，仿真结果表明所提算法能较好地解决杂波环境下跟踪多机动目标的数据关联问题。文献［8］研究了有源雷达系统下多传感器多目标的检测跟踪问题，并通过仿真验证了所提算法能克服JPDA算法在多传感器多目标跟踪中的缺陷，提高跟踪精度。为了有效解决杂波条件下的多目标检测跟踪问题，本文提出一种基于拟蒙特卡罗智能粒子滤波联合概率数据关联［9-12］（Quasi Monte Carlo Intelligent Particle Filter-Joint Probabilistic Data Association，QMC-IPF-JPDA）的无源协同定位算法。该算法首先建立双基站无源协同定位系统目标检测跟踪的数学模型。其次，通过拟蒙特卡罗技术使粒子分布更加均匀，并对更新阶段的粒子进行交叉变异以提高粒子多样性。最后，结合测量信息，利用联合概率数据关联算法实现多目标检测跟踪。

1 系统模型

1.1 目标运动模型

假定在双基站无源雷达探测区域内存在M个目标，则记目标在第k帧的运动状态为，其中和分别表示目标t第k帧在x，y方向的位置和速度。在雷达探测周期内，目标近似做匀速直线运动，其运动方程可表示为：

其中，为目标状态转移矩阵，I2为二阶单位阵，⊗为Kronecker积，△为测量周期，为服从均值为零，方差为高斯分布的过程噪声，G为输入噪声矩阵：

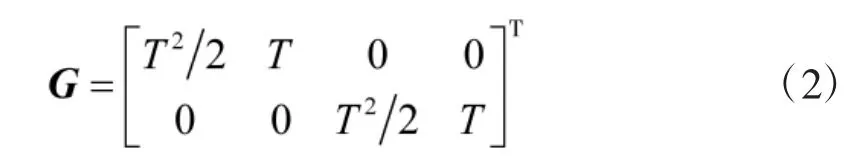
1.2 双基站外辐射源雷达测量模型

双基站无源协同定位系统如图1所示，其中Tx表示外辐射源，Rx表示接收站，Ox表示目标，dOR表示Ox与Rx间的距离，dOT表示Ox与Tx间的距离，dRT表示Rx与Tx间的距离。

双基站无源协同定位系统中目标的测量模型为：

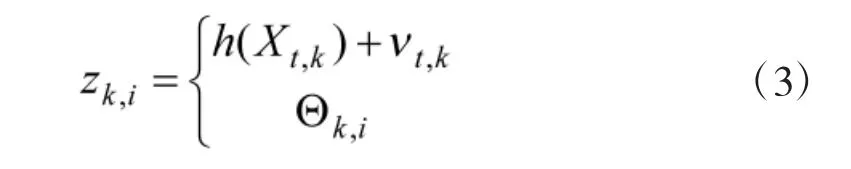
图1 双基站外辐射源雷达目标定位示意图

其中，zk，i为第 k 帧第 i个测量；Θk，i为杂波；vt，k为测量噪声，满足均值为零，协方差为Rt，k的高斯分布，且与相互独立；为目标状态 Xt，k在测量空间中的非线性映射：

其中，和分别表示Rx和Tx的位置，表示目标位置。假设第k帧测量个数为mk，则第k帧测量集合。

2 QMC-IPF-JPDA算法

2.1QMC-IPF算法

QMC-IPF算法的基本思想是：通过拟蒙特卡罗技术改善IPF中粒子的分布特性，快速实现粒子多样化，降低粒子数量提高算法的实时性。假设粒子初始分布概率密度p（X0）已知，粒子数为N。首先采用QMC技术根据低偏差Halton序列产生粒子样本，获取区间［0，1］内的低偏差点集和。其次，第0帧时根据p（X0）进行采样得到粒子数为N的粒子集，根据将粒子集映射到探测区所对应的位置并计算粒子权重。根据粒子权重高低归类粒子状态。将上述步骤产生的按照权重降序排列，可得小于门限权重和大于门限权重的粒子状态集合。最后通过交叉、变异和重采样得到新的粒子集。

2.2 JPDA算法

假设第k帧M个目标的候选回波个数为mk，则候选回波与目标的隶属关系可用确认矩阵表示，其中为二进制变量，表示测量落入目标的确认门内，=0表示测量没有落入目标的确认门内。t=0时表示没有目标，此时ωi，0的列元素全为1，所有测量都为杂波或虚警。记表示测量源自目标的事件，表示测量源自杂波或虚警，则条件概率为：

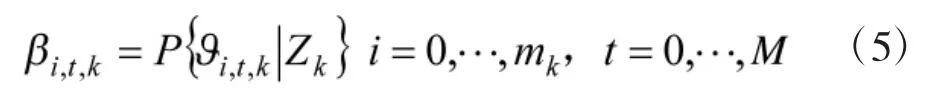
其中，表示测量源自目标的互联概率，，则可分解为：。其中表示第s个联合事件，nk表示联合事件的个数。在联合事件中，当测量源自目标为1，否则为0。则由贝叶斯理论可得：

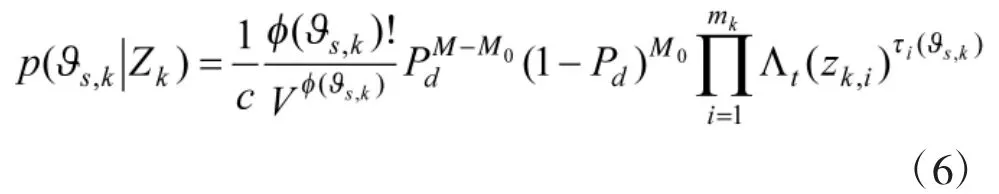
其中，M0表示未检测到的目标数量，V表示目标有效门的体积，Pd表示目标检测概率，表示测量 zk，i对目标 t的似然。

2.3 QMC-IPF-JPDA算法

QMC-IPF-JPDA算法基于联合概率数据关联算法基本框架，结合拟蒙特卡罗智能粒子滤波算法，通过粒子来表示每个目标的边缘分布，处理非线性非高斯模型下的多目标跟踪问题。QMC-IPF-JPDA基本算法流程如下所示：

步骤1：已知第k-1帧目标t的样本及第k帧测量Zk。

步骤2：采集新样本，，并计算样本似然。

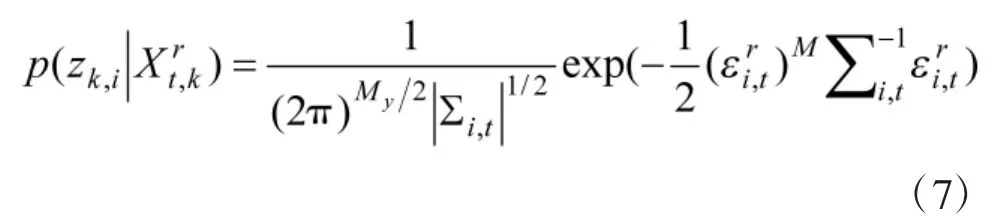
其中，My表示测量的维数，表示测量 zk，i与样本的新息，∑i，t表示目标t的样本以最小均方估计的形式得到的新息协方差矩阵。

步骤3：计算关联事件的后验概率。

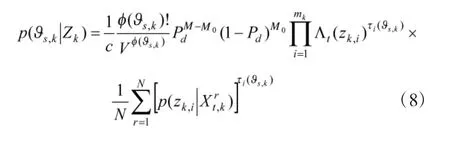
步骤5：各个目标样本独立重采样，，其中分别为第k帧目标t重采样前的第h个样本及对应的权重。

步骤6：估计目标状态：。

步骤7：转入步骤2进行迭代。

3 仿真分析

为了说明所提算法的有效性和性能优势，本节通过两个典型场景并采用QMC-IPF-JPDA和PF-JPDA两种算法实现多目标的检测跟踪。场景参数如下：目标个数为2，探测时间为100 s，测量周期为1s，Rx的位置为［0km，0km］，Tx的位置为［0km，12 km］。算法参数：蒙特卡罗仿真50次，正确量测落入跟踪门内的概率为0.99，检测概率为1，关联波门门限为9.21，每个单位面积内产生3个杂波。计算机参数如下：Intel i5 CPU M480，内存2 GB，32位操作系统，仿真软件为MATLAB2013a。

3.1 场景1：目标分离运动

目标A的初始运动状态矩阵为［3 km，0.3 km/s，5 km，0.2 km/s］T，目标B的初始运动状态矩阵为［5 km，0.3 km/s，1 km，0.15 km/s］T。图 2 给出了原始测量数据和跟踪效果图，从图中可以看出目标原始测量分布密集，无法直接区分测量为杂波还是源自目标的测量表明目标信号弱，受到强杂波干扰，从目标估计状态可知QMC-IPF-JPDA算法能有效检测跟踪目标。

图2 目标分离运动时原始测量与跟踪效果图

下页图3（a）和（b）分别给出了两目标分离运动时，QMC-IPF-JPDA算法和PF-JPDA算法分别对目标A和目标B状态估计的RMSE，通过对比两种算法得到的目标跟踪RMSE可知，所提算法能降低跟踪误差，提高目标跟踪精度。

表1给出了不同参数对QMC-IPF-JPDA算法目标跟踪精度的影响，从表1可知，随着单位面积内杂波个数的增加，算法跟踪误差随之增大，降低了算法跟踪精度。

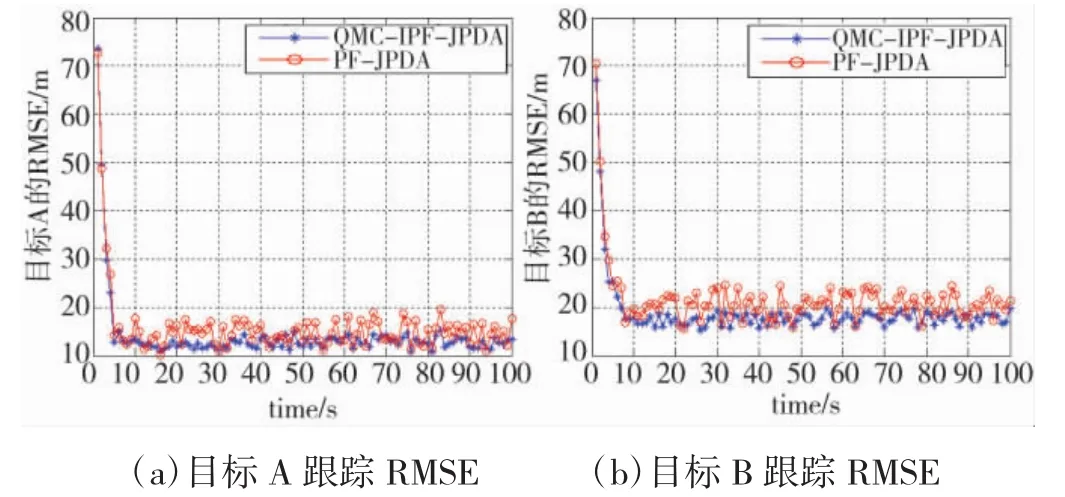
图3 两种算法目标跟踪RMSE

3.2 场景2：目标交叉运动

当两个目标相距较近时，源于目标的测量会相互干扰，导致误跟现象的发生。为了验证所提算法对相距较近两个目标的跟踪有效性，假设目标A的初始运动状态矩阵为［3 km，0.3 km/s，5 km，0.1 km/s］T，目标B的初始运动状态矩阵为［5km，0.2km/s，1 km，0.15 km/s］T。图4给出了两目标交叉运动时雷达的原始测量数据与算法跟踪效果图，从图中可知，本文所提算法QMC-IPF-JPDA能有效处理杂波环境下的多目标交叉运动的检测跟踪问题。

表1 不同单位面积内杂波个数对算法跟踪精度影响（米）

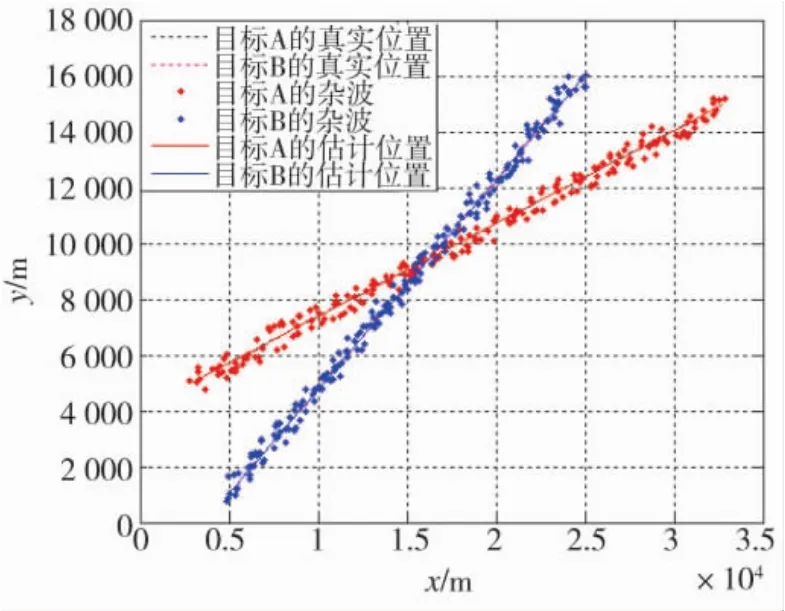
图4 目标交叉运动时原始测量与跟踪效果图

图5（a）和（b）分别给出了两目标交叉运动时，QMC-IPF-JPDA算法和PF-JPDA算法分别对目标A和目标B状态估计的RMSE，通过对比两种算法得到的目标跟踪RMSE可知，所提算法能降低跟踪误差，提高目标跟踪精度。

表2给出了不同粒子数下两种算法单帧处理时间，结合表2、图3和图5可以看出，所提QMC-IPF-JPDA算法相比PF-JPDA牺牲少量的实时性，较大地提高了对目标的跟踪精度，该算法适用于对跟踪精度较高的场景。

4 结论

本文针对复杂环境下多目标的检测跟踪问题，提出一种基于QMC-IPF-JPDA的多目标无源协同定位算法。仿真结果表明，本文所提算法能有效解决杂波条件下多目标的检测跟踪问题，降低跟踪误差，提高检测跟踪性能。后续将重点研究目标个数未知的检测跟踪问题。

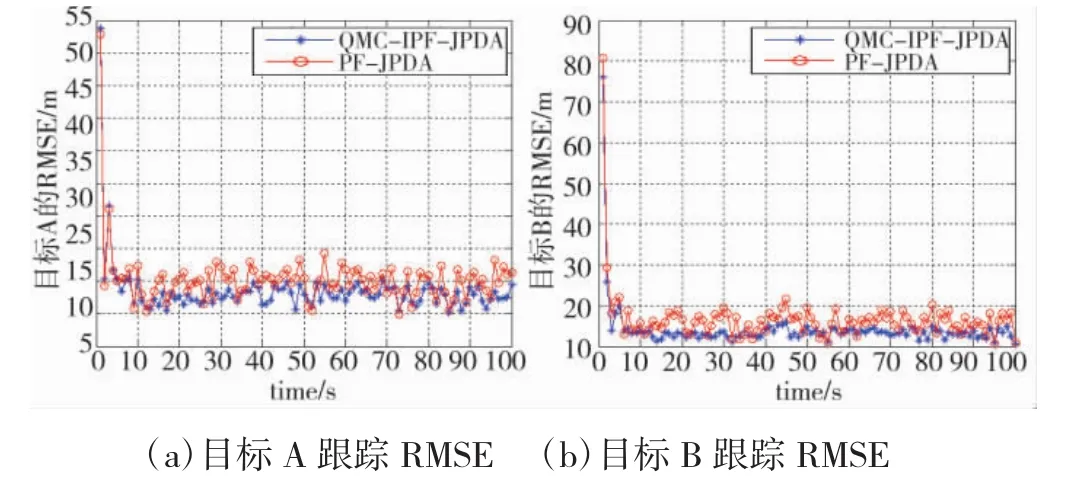
图5 两种算法目标跟踪RMSE

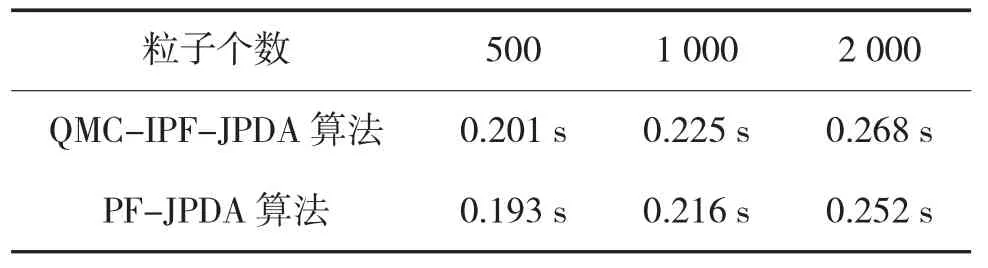
表2 不同粒子数时算法的单帧处理耗时（s）

［1］COLONE F，LOMBARDO P.Polarimetric passive coherent location［J］.IEEE Transactions on Aerospace and Electronic Systems，2015，51（2）：1079-1097.

［2］RADMARD M，KARBASI S M，NAYEBI M M.Data fusion in MIMO DVB-T-based passive coherent location ［J］.IEEE Transactions on Aerospace and Electronic Systems，2013，49（3）：1725-1737.

［3］吴兆平，朱凯然，苏涛.采用改进粒子滤波的雷达扩展目标检测前跟踪［J］.西安电子科技大学学报（自然科学版），2011，38（2）：99-104.

［4］关欣，胡东辉，仲利华.一种高效的外辐射源雷达高径向速度目标实时检测方法［J］.电子与信息学报，2013，35（3）：581-588.

［5］COLONE F，O'HAGAN D W，LOMBARDO P.A multistage processing algorithm for disturbance removal and target detection in passive bistatic radar［J］.IEEE Transactions on Aerospace and Electronic Systems，2009，45（2）：698-722.

［6］郭云飞，杜巍，林岳松.一种基于粒子滤波的概率数据关联方法［J］.火力与指挥控制，2010，35（10）：28-30.

［7］朱志宇，皇丰辉，姜长生.杂波环境下的粒子滤波器数据关联方法［J］.电光与控制，2008，15（2）：50-54.

［8］耿峰，祝小平.一种改进的多传感器多目标跟踪联合概率数据关联算法研究［J］.系统仿真学报，2007，19（20）：4671-4675.

［9］JIN N G，LI F M，LI Z X.Quasi-Monte carlo gaussian particle filtering acceleration using CUDA ［J］.Applied Mechanics and Materials，2011：3311-3315.

［10］YIN S，ZHU X.Intelligent particle filter and its application to fault detection of nonlinear system［J］.IEEE Transactions on Industrial Electronics，2015，62（6）：3852-3861.

［11］耿利祥，陈钱，钱惟贤.改进的联合概率数据关联算法对红外目标与诱饵的辨别［J］.红外与激光工程，2013，42（2）：305-310.

［12］BOJILOV L V，ALEXIEV K M，KONSTANTINOVA P D.An accelerated IMM JPDA algorithm for tracking multiple manoeuvringtargetsin clutter ［C］//5th International Confererence on Numerical Methods and Application，2002，2542：274-282.