基于AM-LFM与BOMP的ISAR成像算法*

卢丁丁 ，张智军 ，杨博楠 ，马 赢 ，2，肖冰松

（1.空军工程大学航空航天工程学院，西安 710038；2.解放军95662部队，拉萨 850000）

0 引言

逆合成孔径雷达（Inverse Synthetic Aperture Radar，ISAR）微动目标成像具有成像时间内目标姿态不断变化的特点，姿态不断运动引起微动目标的多普勒频率和成像平面的不断变化［1-4］，会对微动目标的成像造成散焦，使得传统成像方法难以获得目标清晰像。微多普勒信号的频谱将随时间在一个较大范围内变化，因而目标的微多普勒效应可能会遮挡目标的大部分主体部分的图像，即在成像过程中会污染目标主体部分的成像，使得目标难以被识别出来［5-6］。针对含微动目标的稀疏孔径ISAR成像问题，文献［7］提出了一种基于 Chirplet［8］变换和 CS重构的含旋转部件目标稀疏孔径ISAR成像算法（以下简称Chirplet-CS算法）。该算法在Chirplet基下，将目标回波信号展开为函数加权的形式，通过微动目标回波中主体部分和旋转微动部分在Chirplet基下的差异性，将分别分离出目标主体部分的信号和微动部分的信号，再引入CS理论，利用微动目标的方位向回波在频域具有的稀疏性进行目标主体部分的稀疏成像。

基于Chirplet分解和CS微动目标稀疏孔径成像算法，对含微动运动的目标进行ISAR成像取得了较好的成像效果。但该算法存在两个方面的不足，一是算法使用的Chirplet函数分解，Chirplet分解存在运算量大的缺点；二是在缺少先验信号稀疏度信息的条件下，为不丢失信号，正交匹配追踪［9-12］（Orthogonal Matching Pursuit，OMP）重构算法需要预设一个比稀疏度真值大得多的算法支撑集，这会导致算法重构结果的稀疏度高于真实值，加剧了算法的计算量，并且会分散真实信号能量，使得重构精度与鲁棒性变差。针对算法存在的不足，提出基于调幅-线性调频（Amplitude Modulation-Linear Frequency Modulation，AM-LFM）分解和贝叶斯正交匹配追踪（Bayesian Orthogonal Matching Pursuit，BOMP）的改进微动目标成像算法。

本文围绕稀疏采样下的微动目标聚焦成像问题展开研究，引入CS技术用于处理所引起的成像困难。针对基于Chirplet分解和CS的微动目标稀疏孔径成像算法存在计算量大和重构精度、鲁棒性差的缺点，引入AM-LFM分解与BOMP重构方法，提出改进成像算法。最后对比两种仿真算法，证明了改进算法的有效性。

1 调幅-线性调频分解与分离

文献［13］提出，一系列的调幅-线性调频（AMLFM）可以拟合成目标多普勒信号，如图1所示。

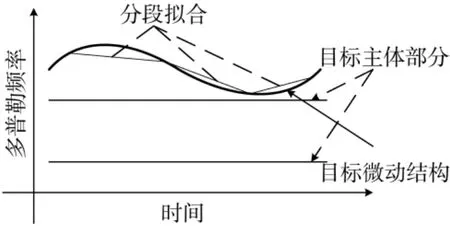
图1 目标多普勒信号拟合图

在传统的目标ISAR成像中，含微动部件的目标雷达回波可以分解成：

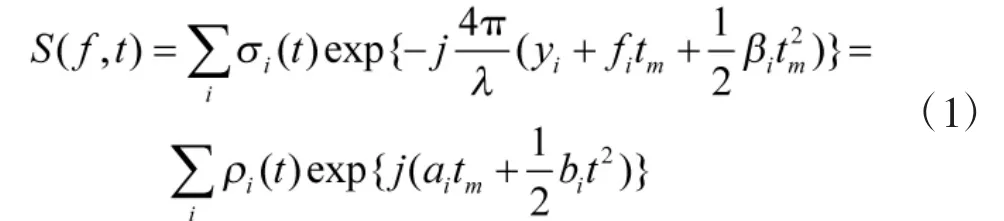
其中，ai为起始调节频率，βi为调节频率，ρi（t）称为调幅函数。文献［11］提出，雷达对目标主体的回波可以近似为βi≈0，而微动结构的回波则为βi≠0。因此，能够根据各信号分量调频率的值，采用基于CLEAN的思想对经过AM-LFM分解后的表示目标散射点信号的原子集进行分离，从而实现微动目标主体回波信号和微动结构回波信号的分离。目标信号AM-LFM分解与分离的流程如图2所示。

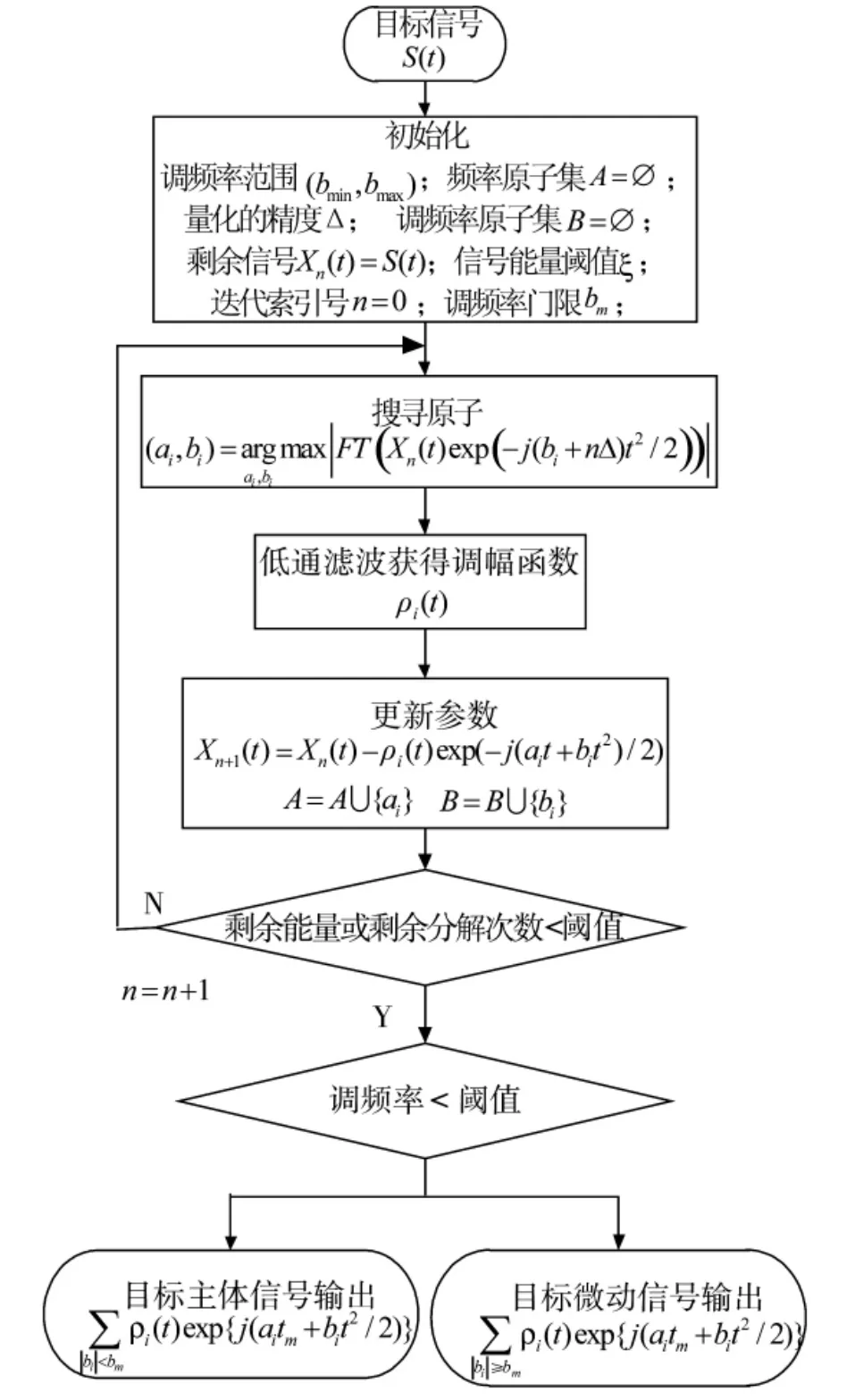
图2 目标信号AM-LFM分解与分离流程图

2 贝叶斯正交匹配追踪（BOMP）算法

BOMP算法是在OMP算法重构输出支撑集的基础上，将其留作候选集，并使用Bayesian检验模型筛选该集中的原子，以剔除掉其中的冗余原子部分，再基于迭代筛选后保留下来的原子集作为新支撑集进行重构。该算法可有效减少计算量，增强重构精度和抗噪性［14-16］。

在CS理论中，对信号，存在稀疏变换基，使信号x满足稀疏性，可通过测量矩阵得到信号的量测值（考虑信号在噪声条件下）为：

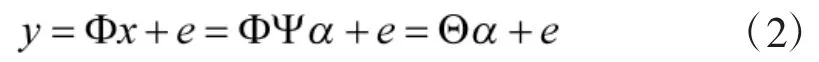
当Θ满足RIP时，求解：

可将信号x从降维观测y恢复出来。

在式（2）中，假定噪声向量e满足高斯分布（I表示单位矩阵），可用贝努利高斯模型［17］分析信号α，若信号中的元素αi为零的概率为p，则不为零的概率为1-p，且该元素不为零时其幅值满足高斯分布，即。其中qi在αi≠0 时为 1，其余为 0，记。那么α可以表示为，得到信号的贝努利高斯模型后采用Bayesian检验模型对信号支撑集中的原子进行筛选如下：

假设概率参数p值已给出，依据经验设定信号粗略估计的稀疏度为K0（K0仅是初步设定的冗余值，并不等于信号的真实稀疏度）。就可构造信号的Bayesian检验模型来不断消去粗略估计稀疏度K0的多余成分。由于，可知q的条件概率密度函数为：

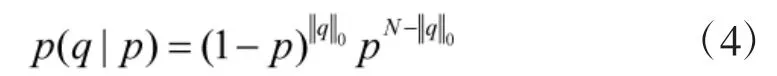
若将信号α中的非零元素组建一个新的向量w，则有，若已知，则w的概率密度函数可以表示为：

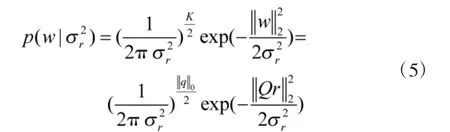
则在已知的条件下，量测值y的概率密度函数可表示为：

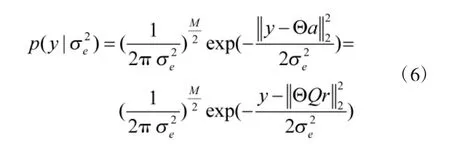
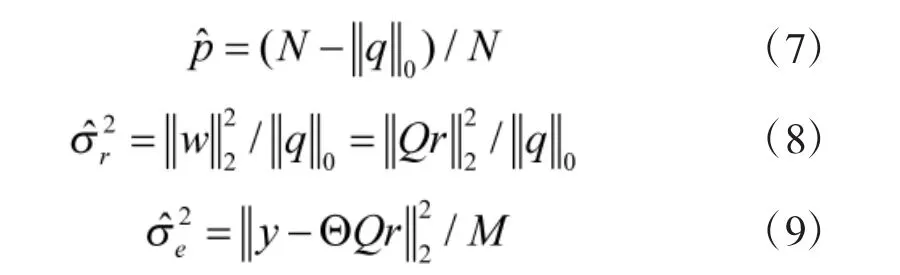
以上3个公式即为基于Bayesian模型的参数估计表达式。

根据Bayesian假设检验模型组成似然比函数筛除掉通过OMP算法输出的候选集中的冗余元素，详细推导过程可参阅文献［18］，依据该文献的结论可得似然比检验公式为：

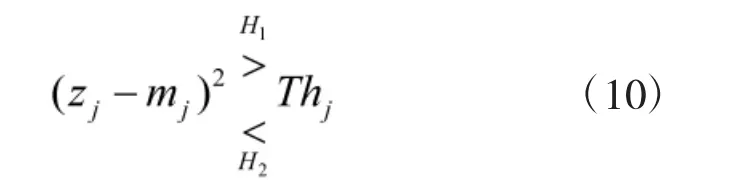
其中，

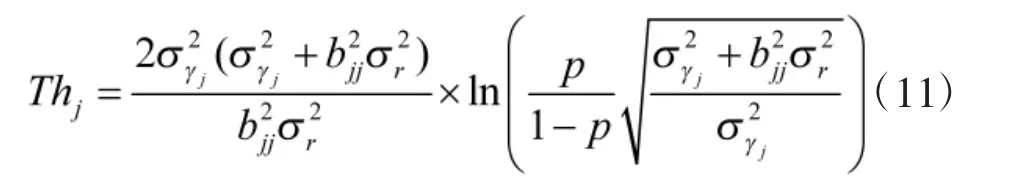
依据式（10）中的判别准则，在的条件下，事件 H1（信号 αi≠0）成立，保留候选支撑集中的元素αi并更新支撑集；相反的，在的条件下，事件H0（信号αi=0）成立，剔除候选支撑集中的元素αi并更新支撑集。这样对候选集中的元素进行筛选剔除处理后就可估计出信号的最终支撑集，最后可采用最小二乘法重构出信号。

综合上述分析，BOMP算法的具体流程可归纳总结为：

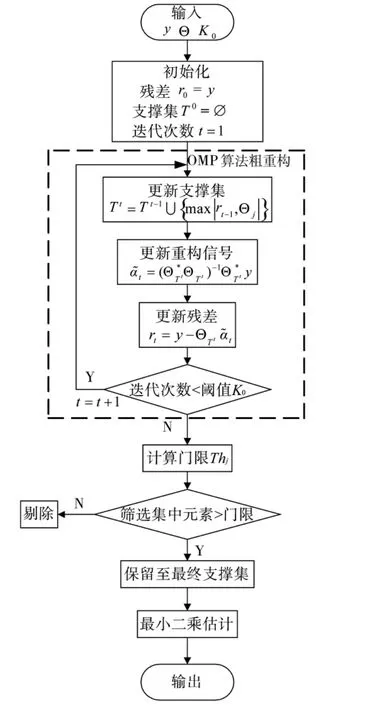
图3 BOMP追踪算法流程图

3 改进微动目标成像算法流程

基于上述的讨论分析，提出基于AM-LFM和BOMP的改进微动目标成像算法，算法流程示意图如图4所示。

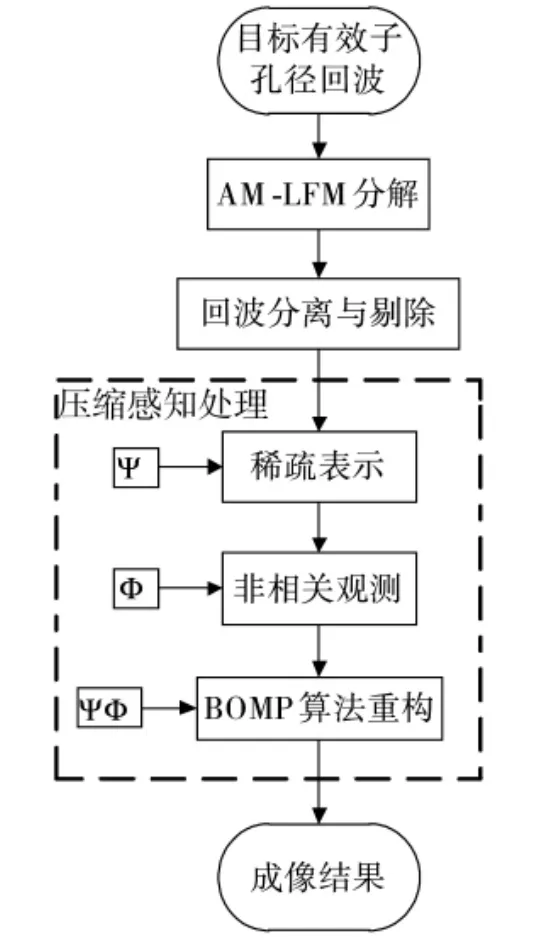
图4 基于AM-LFM和BOMP的改进算法流程图

基于AM-LFM和BOMP的改进微动目标成像算法详细步骤如下：

步骤1和步骤2：AM-LFM分解与回波分离与剔除。AM-LFM分解与回波分离与剔除具体步骤如图1，此处不再重复说明。

步骤3：稀疏表示。目标方位向回波信号在频域满足稀疏性，因此，可以运用CS理论对微动目标的主体部分成像。算法中选用逆离散傅立叶变化（IDFT）作为稀疏基构建稀疏变化矩阵，对经过步骤2中分离剔除掉目标微动部分散射点回波后的距离单元信号进行稀疏表示，并得到信号稀疏度。

步骤4：非相关观测。该算法根据有效子孔径的稀疏结构构建有效测量矩阵Φ，用于获得微动目标的主体部分散射点回波信号低维的观测值，即压缩测量数据。测量矩阵Φ可表示为：

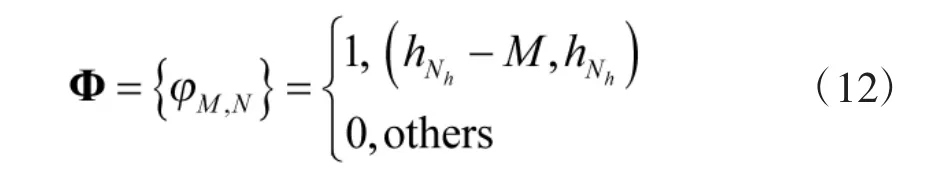
式中，是第h段子孔径回波中第Nh个脉冲的序号，M为第h段子孔径前回波缺失的脉冲总数。

步骤5：BOMP算法重构。信号经过上述步骤处理后可得到回波信号稀疏度K、压缩测量数据y，然后再经过BOMP重构算法就可得到稀疏信号的最终估计。BOMP重构算法在OMP重构算法的基础上将OMP算法中的支撑集留作候选集，利用Bayesian检验模型筛选该集中的所有原子以剔除掉其中的冗余部分，再基于筛选后的新支撑集进行信号重构。详细实现流程如下：

1）初始化：剩余信号为r=y，支撑集，迭代次数k=1；

2）OMP算法粗重构：先对信号使用OMP重构算法，就可得到初步的支撑集和初步的重构回波信号，用于后续Bayesian检验模型的筛选与剔除，详细处理过程可参照OMP算法的具体实现流程；

3）筛选与剔除：以初步的支撑集作为候选集，将其维度作为‖q‖0的估值，初步的重构信号作为Qr的估值，可计算出门限值Thj，然后筛选出候选集中大于门限的元素并保留作为最终支集；

4）最小二乘法估计：使用最小二乘法对信号估计取得其最终的估计值，进而获得目标最终成像。

4 实验仿真及分析

4.1 算法定性对比仿真实验

为了便于直观对比实验效果，采用欧洲直升机公司制造的AS350直升机模型仿真数据对算法进行仿真验证。AS350直升机的旋翼由3片直径为10.69 m的旋转叶片组成，转速约为6.6 r/s；尾翼由2片直径为1.86 m的旋转叶片组成，转速为34.8 r/s；假设每个旋转叶片等效于中部和顶端散射点组成的点散射模型，其中雷达发射线性调频（LFM）信号，脉宽为 Tp=1 μs，信号载频 fc=10 GHz，带宽B=600 MHz，脉冲重复频率PRF=1000 Hz。直升机散射点模型的运动参数与成像雷达取孔径稀疏度为50%，在上述条件下进行仿真实验。这里主要对比Chirplet-CS算法与改进CS（基于AM-LFM和BOMP改进）微动目标成像算法以及传统傅里叶ISAR成像效果获得的目标ISAR像效果图，如下页图5所示。

对比改进CS算法得到的ISAR像（图5（c））、Chirplet-CS算法得到的ISAR像（图5（b））的成像与传统傅里叶ISAR算法得到的图像（图5（a））。由图5的结果可知：传统傅里叶ISAR算法图像中微动部分的回波信号与其主体部分回波信号重叠，严重干扰了直升机主体回波信号，获得的目标直升机ISAR图像聚焦性较差，难以从图像中识别和分辨出目标；而稀疏条件下基于CS的两种方法则可重构出目标较好的成像，将图5（b）和图5（c）加以对比可知改进CS算法得到的目标像（图5（c））在细节处成像效果要好于Chirplet-CS算法得到的成像（图5（b）），实验结果符合理论分析中的结论（BOMP重构精度优于OMP重构精度）。

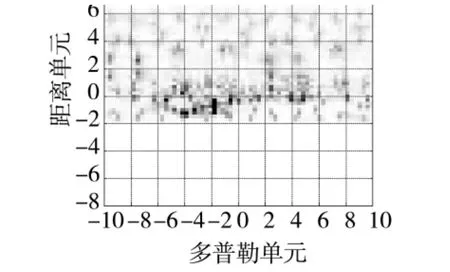
图5（a） 传统傅里叶ISAR成像效果图

图5（b） Chirplet-CS算法得到的ISAR像

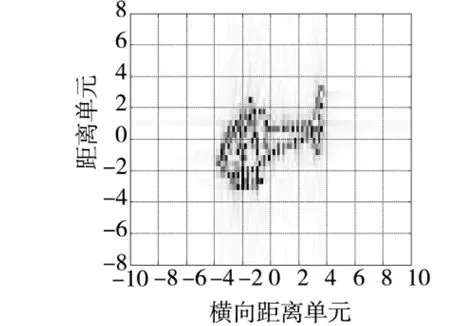
图5（c） 改进CS算法得到的ISAR像

4.2 算法定量对比仿真实验

为了定量分析提出的改进CS算法微动目标成像的算法性能，仿真从算法的重构精度、鲁棒性与计算效率3方面展开，对比分析了改进算法与原算法的性能。

仿真1：重构精度与鲁棒性分析

算法的重构性能可以由实际成像结果的重构误差与最终估计矢量â的克拉美罗下界（Cramer-Rao lower bound，CRLB）进行对比分析可得，鲁棒性可由不同信噪比条件下算法的重构误差对比可得，仿真中输入不同信噪比的信号，设定信噪比SNR=0∶2∶12 dB，蒙特卡罗仿真次数取500次，实验结果如图6所示。

由图6分析可知，随着输入信噪比值的不断增大，两种算法的重构误差均表现出不断减少的趋势，且不断趋近于理论的CRLB值。输入信噪比值较低时，改进算法的重构误差低于原算法，更靠近CRLB值，且由图6可以看出改进算法受噪声的影响小于原算法。因此，改进算法在低信噪比的重构精度与鲁棒性要优于原算法。这符合算法的原理分析（因为原算法采用OMP重构，改进算法采用BOMP重构）。

仿真2：计算效率分析

从算法的原理分析可知，改进算法与原算法的计算量差异主要由两部分组成，一部分是在信号分解时产生的，原算法使用Chirplet分解而改进算法采用AM-LFM分解，Chirplet分解运算量大，因此，可知信号分解中改进算法的计算量将明显小于原算法；另一部分计算量差异是在CS重构中产生的，主要来源是因为改进算法的BOMP重构中需要在原算法OMP粗重构的基础上筛选支撑集，此计算量为部分矩阵的加与乘，可忽略不计。在缺少先验信号稀疏度信息的条件下，OMP重构算法要预设一个冗余稀疏度支撑集，加剧了算法的计算量。运算时间如图7所示。

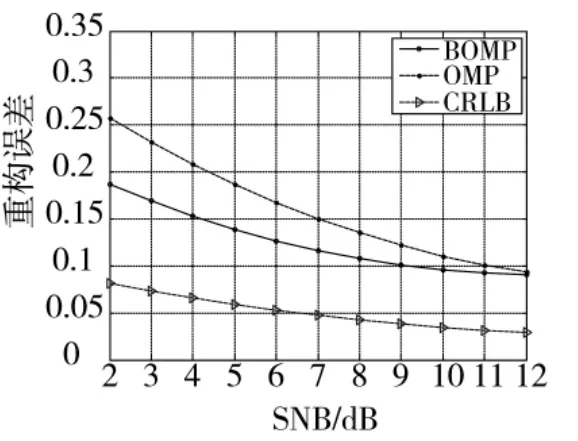
图6 重构误差与鲁棒性对比分析仿真结果图

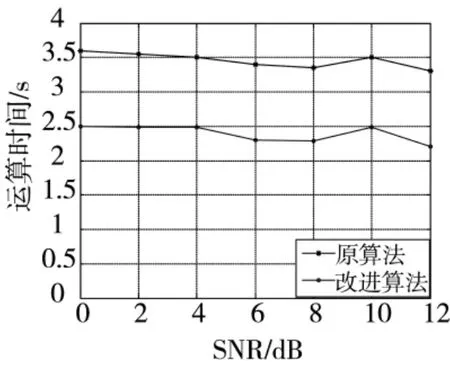
图7 仿真运行时间比较图

从仿真运行时间对比中可以看出，改进算法的计算量要明显少于原算法，仿真验证了BOMP算法具有重构速度快的优势。

5 结论

本文针对稀疏采样下微动目标的ISAR成像问题展开研究，针对基于Chirplet变换和CS技术的含旋转部件目标稀疏孔径ISAR成像算法存在的运算量大、重构精度与鲁棒性差的缺点，引入了基于AM-LFM分解和BOMP重构的算法。这种改进CS算法可以有效消除微多普勒效应，并生成聚焦良好的主体部分二维像；最后进行仿真对比，实验验证该改进CS算法在稀疏采样条件下的有效性与其成像优势，结果表明针对目标成像的改进算法在计算量、重构精度、鲁棒性优于原算法，且其运算效率得到明显提高。

［1］CHEN V C，LI F，HO S，et al.Micro-doppler effect in radar：phenomenon，model，and simulation study［J］.IEEE Transactions on Aerospace and Electronic Systems，2006，42（1）：2-21.

［2］RICHARDS M A，SCHEER J A，HOLM W A.Principles of modern radar［M］.Chennai：SciTech Publishing，2010.

［3］SPARR T，KRANE B.Micro-Doppler analysis of vibrating targets in SAR ［J］.Proc.Inst.Electr.Eng，Radar Sonar Navig，2003，150（4）：277-283.

［4］CHEN V C，LING H.Time-frequency transforms for radar imaging and signal analysis［M］.Boston：Artech House，USA，2002.

［5］WANG Q，XING M D，LU G Y，et al.High resolution three-dimensional radar imaging for rapidly spinning targets［J］.IEEE Trans Geosci Remote Sens，2008，46（1）：22-31

［6］BAI X R，XING M D，ZHOU F，et al.High-resolution three-dimensional imaging of spinning space debris［J］.IEEE Trans on Geoscience and Remote Sensing，2009，47（7）：2352-2362.

［7］徐艺萌，管桦，罗迎，等.含旋转部件目标稀疏孔径ISAR成像方法［J］.空军工程大学学报（自然科学版），2013，14（4）：57-61

［8］尉宇，孙德宝，岑冀刚.高斯线调频小波变化及参数优化［J］.电子与信息学报，2005，27（9）：1398-1403.

［9］JAIN A.K.Fundamental of digital image processing［M］.New Jersey：Prentice Hall，1989.

［10］TIPPING M E，FAUL A.Fast marginal likelihood maximization for sparse Bayesian models［C］//Proceedings of the Ninth International Workshopon Artificial Intelligence and Statistics，Key West，Florida，2003：1-13.

［11］FIGUEIREDO M.Adaptive sparseness using Jeffreys prior［C］//Advances in Neural Information Processing Systems 14th，Vancouver，2002：697-704.

［12］DAVENPORT M A，WAKIN M B.Analysis of orthogonal matching pursuit using the restricted isometry property［J］.IEEE Trans.on on Information on Theory，2010，56（9）：4395-4401.

［13］贺思三，周剑雄，赵会宁，等.基于AM-LFM分解的微动信号提取［J］.电子学报，2010，32（3）：554-558.

［14］方红，杨海蓉.贪婪算法与压缩感知理论［J］.自动化学报，2011，37（12）：1413-1421.

［15］CAI T T，WANG I.Orthogonal matching pursuit for sparse signal recovery with noise ［J］.IEEE Trans.on Information Theory，2011，57（7）：4680-4688.

［16］李少东，杨军，马晓岩.基于压缩感知的ISAR高分辨成像算法［J］.通信学报，2013，34（9）：150-157.

［17］ZAYYANI H，BABAIE-ZADEH M，JUTTEN C.An iterative bayesian algorithm for sparse component analysis in presence of noise［J］.IEEE Trans.on Signal Processing，2009，57（11）：4378-4390.

［18］甘伟，许录平，苏哲，等.基于贝叶斯假设检验的压缩感知 重 构 ［J］. 电子与信息学报，2011，33（11）：2640-2646.