对于转向梯形的一种新的设计方法

2018-06-13李龙飞李龙强龚利全

时代汽车 2018年11期

李龙飞李龙强龚利全

河南速达电动汽车科技有限公司技术中心河南省三门峡市 472000

1 引言

转向梯形机构的作用是通过分配内外轮转角来保证汽车的转向性能。通过对大部分的乘用车进行分析和研究，传统的转向梯形机构运动简图并不够理想，因此在本文提出了一种新的转向梯形机构的设计和分析方法。本文为了使转向梯形机构问题得到更加清晰的描述和对两种方法之间进行对比，所以对传统的方法也进行了简单地阐述。

2 汽车转向梯形的概述

为保证车轮尽可能作纯滚动而减少滑动，由图1可知，实际的内外车轮转角关系应尽可能接近理论内外转角关系，理论特性应尽可能满足阿克曼公式：

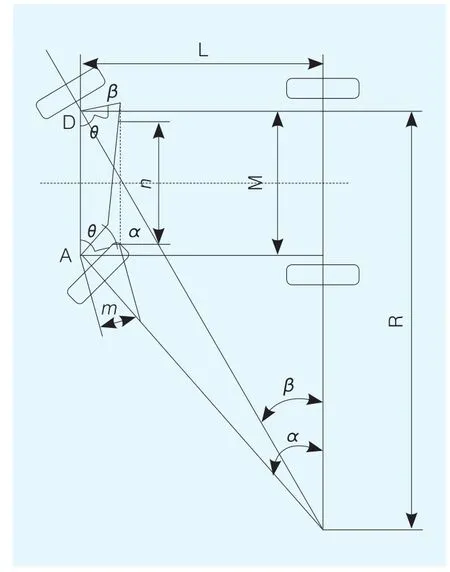
图1 汽车转向运动分析图

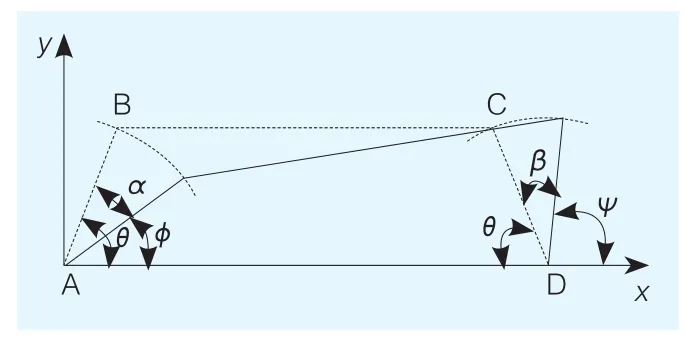
图2 转向梯形坐标系

汽车转向梯形是由转向器的齿条、左右转向横拉杆、左右转向节臂和前桥等部分组成的以实现良好转向性能为目的的运动机构，转向梯形设计的好坏直接影响转向系统的两个运动特性：第一个就是最小转弯半径，第二个就是阿克曼公式的契合度。最小转弯半径是汽车机动性的主要指标之一，它反映了汽车通过小曲率半径弯曲道路和狭窄路面、场地上调头的能力。阿克曼公式的高契合度可以保证汽车内外轮尽可能作纯滚动运动，以使轮胎在很大程度上减少与地面发生的相对滑动而带来的胎面磨损。

由图1可知，最小转弯半径Rmin主要取决于最大外轮转角βmax、轴距L和主销偏置距rs，其关系为：

3 传统的设计方法介绍

目前工程设计人员大多都是按经验数据选择转向梯形机构的各几何参数，然后将转向梯形机构简化为平面四杆机构来进行分析，最后通过传统的图解法进行分析校核，其主要步骤如下。

首先建立坐标系（见图2），然后通过解析几何的方法求解出其内外轮转角关系的方程式：

然后根据经验给出各几何参数，接着采用第一种作图法进行分析校核，解出若干个实际点并将其绘制在图3中，例如若实际点i的α和β已求出，则∠iAD=α，∠iDA=β，即可求出点i在图3中的位置。接着用作图法在图3中将若干实际的点连接成一个实际特性曲线GE。接着按同样的道理绘制理想特性曲线，由平面几何知识可推出理想特性曲线实际上是一条直线（证明：从第i点和第i+1点分别做垂线Hi和Hi+1垂直于AD，得到cotβi-Lβi和ΔH的比值始终为定值

或者采用第二种作图法进行分析校核，见图4。

最后将实际特性曲线GE同理想特性曲线GF（阿克曼曲线）进行比较，若Δβmax小于允许偏差则满足设计要求，否则重新选择梯形参数，重新作图。

3 新的机构运动简图及其设计分析方法

3.1 对传统方法的评价

对于传统方法有以下不足：

首先是机构简图与实际有出入，一般乘用车上的转向器是齿轮齿条式的，而且转向器是固定在副车架上的，基本上在汽车转向运动时转向器与主销连线平行，其机构运动应简化为图5来分析较为合理。

其次是传统的作图法设计虽然直观方便，但作图过程较为麻烦，数据的全面性也存在不足。随着计算机技术发展，可以将目前的技术成果运用到工程实际当中，建立起一种新的设计方法。该方法可以使设计者感到直观方便，也可以减少设计者的设计校核的工作量。

图3 第一种作图法实际特性曲线同理想特性曲线对比

图4 第二种作图法实际特性曲线同理想特性曲线对比

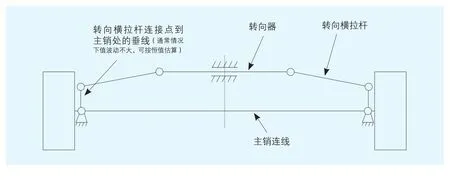
图5 新的转向机构运动简图

图6 初始简图

图7 第一步等效简图

3.2 新的机构运动简化模型

为了能够得到新的机构运动简图的分析方程，需要将该简图做进一步简化。

a.初始简图见图6。

b.将初始简图分解成等效简图，这里简称第一步等效简图，见图7。

c.从本页纸的背面看，可以发现汽车转向时右侧的简图与左侧简图运动轨迹正好相反，见图8。图8在这里简称第二步等效简图，建立第二步等效简图的目的是为了方便建立运动方程。

d.对第二步等效简图进行运动分析，将各参数进行标注，即可得到最终简图（见图9），即本文所指的新的转向梯形机构运动简化模型。

说明：

θ——初始角度；

m——转向横拉杆长度；

n——转向横拉杆连接点到主销的垂线，这里简称转向节臂长度；

α——内轮转角；

β——外轮转角；

H——转向器到主销连线的距离；

Δx——转向器平移距离。

3.3 建立新的机构简化模型的方程

首先为最终简图建立坐标系，通过解析几何的方法分析图10可建立下列方程组。

上式即为最终转向梯形机构运动简图的运动方程式。

3.4 最终简图的运动方程式的求解

对于最终简图的方程式，采用Mathematic软件进行求解。这里只需将阿克曼公式和最终简图的方程式进行输入，可得到实际特性曲线与理想特性曲线的矢量图。在设计过程中，首先建立阿克曼曲线上下平移曲线cot（β-1）-cotα=和cot（β+1）-cotα= 以设定允许偏差Δβmax，然后将参数θ、m、n和H设为互动模式，拖动鼠标即可得到与各变量对应的实际特性曲线，将实际特性曲线控制在允许偏差内即可满足设计要求。图11所编写的为Mathematic求解程序。

在Mathematic软件中将程序生成图像（图12），拖动鼠标（或者输入相关参数数值）即可进行参数选取，最后将实际曲线与理论曲线对比即可确定参数值是否满足设计要求。

图8 第二步等效简图

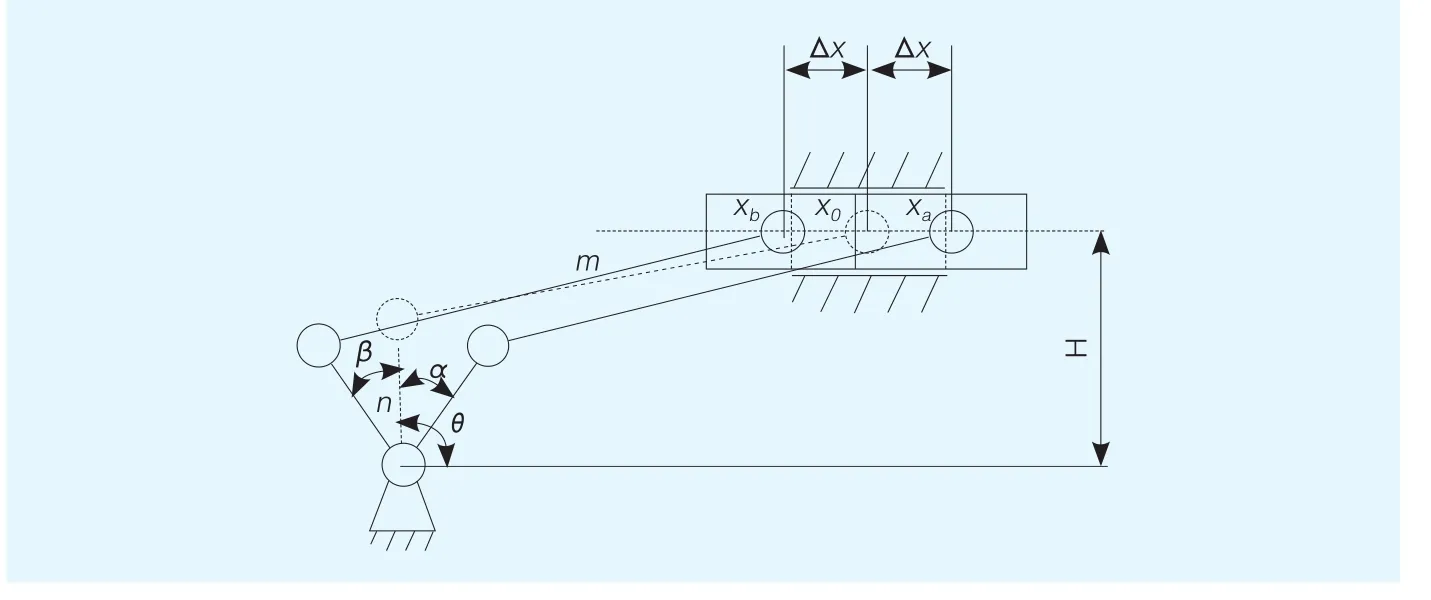
图9 最终简图

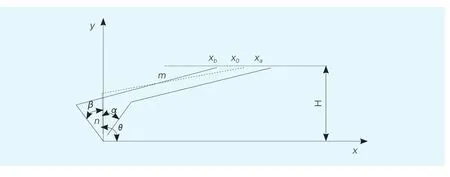
图10 最终简图的坐标系

4 传统方法与新方法的对比

4.1 运动简图

新的转向梯形机构运动简图相比传统机构运动简图更加逼近实际情况。

图11 输入Mathematic软件的程序

4.2 设计方法

新方法和传统方法在图解方面都具备直观易懂的优点，但是新方法在数据上更具有全面性。相比逐个找点然后过渡圆滑成曲线的传统方法，计算机技术的优势很明显就显示出来了，新方法工作效率相比传统方法要高很多，同时工作量也大大减少（拖动拖动鼠标即可完成设计）。在Mathematic软件所生成的图形上，点击鼠标右键还可选择获取坐标值，这样可以先插入较合理的网格线条，然后对具体的某个点进行分析，相比传统方法分析上更为全面一些。还有，Mathematic软件所生成的图即可保存为位图也可保存为矢量图，这样设计者在做技术交流时可以将其设计的转向梯形机构性能得到很好的转述，有利于技术深入地探讨。