Thermodynamics of de Sitter Black Holes in Massive Gravity∗

Yu-Bo Ma(马宇波),Si-Xuan Zhang(张思轩),Yan Wu(邬岩),Li Ma(马立),and Shuo Cao(曹硕),†

1Department of Physics,Shanxi Datong University,Datong 037009,China

2Department of Astronomy,Beijing Normal University,Beijing 100875,China

3Beijing Aerospace Petrochemical Technology and Equipment Engineering Corporation,Beijing 100166,China

1 Introduction

The study of the thermodynamic characteristics of de Sitter space-time has arouse extensive attention in the recent years.[1−17]At the stage of cosmological inflation in the early time,our universe behaves like a quasi-de Sitter space-time,in which the cosmological constant takes the form of vacuum energy.Moreover,if the dark energy is simply a cosmological constant,i.e.,a component with constant equation of state,our universe will evolve into a new stage of de Sitter space-time in this simplest scenario.Therefore,a better knowledge of de Sitter space-time(especially its classical and quantum characteristics)is very important to construct the general framework of cosmic evolution.In the previous works,the black hole horizon and the cosmological horizon are always treated as two independent thermodynamic systems,[4−7,13]from which the thermodynamic volume of de Sitter space-time as well as the corresponding thermodynamic quantities satisfying the first thermodynamics law were obtained.[3]It is commonly recognized that the entropy of de Sitter space-time is the sum of that for the two types of horizons,[7,14]however,such statement concerning the nature of de Sitter space-time entropy still needs to be checked with adequate physical explanation.

Considering the fact that all thermodynamic quantities related to the black hole horizon and the cosmological horizon in de Sitter space-time can be expressed as a function of mass M,electric charge Q,and cosmological constant Λ,it is natural to consider the dependency between the two types of thermodynamic quantities.More specifically,the discussion of the following two problems is very significant to study the stability and evolution of de Sitter space-time:Do the thermodynamic quantities follow the behavior of their counterparts in AdS black holes,especially when the black hole horizon is correlated with that of the cosmological horizon?What is the specific relation between the entropy of de Sitter space-time and that of the two horizons(the black hole horizon and the cosmological horizon)? The above two problems also provide the main motivation of this paper.

On the other hand,to the present,massive gravity has already proven its potential to alleviate the naturalness problem of the cosmological constant[18−20]even in the limit as the graviton mass approaches zero,which can be clearly seen both in the framework of linear gravity theories[21−22]and nonlinear massive gravity theories.[23−24]The ghostlike instability in the latter,which is well known as the Boulware-Deser ghost,has also been extensively discussed in many previous works.[25−26]Moreover,different from the traditional way of simply adding a mass term to the GR action,the new idea of constructing massive gravity theories was fi rstly studied in the context of a charged BTZ black hole,[27]and further well developed in the presence of Maxwell and Born-Infeld electrodynamics in asymptotically AdS space-times.[28]Details of the derived thermodynamic quantities(the corrected entropy,etc.)as well as the corresponding phase transitions may be found in Refs.[29–33].In this paper we expect to provide complementary results on the thermodynamics of dS black hole in massive gravity.

Following this direction,in our analysis we obtain the effective thermodynamic quantities of de Sitter black holes in massive gravity(DSBHMG),based on the correlation between the black hole horizon and the cosmological horizon. Our results show that the entropy of this type of space-time takes the same form as that in Reissner-Nordstrom de Sitter space-time,which lays a solid foundation for deeply understanding the universal thermodynamic characteristics of de Sitter space-time in the future.This paper is organized as follows.In Sec.2,we briefly introduce the thermodynamic quantities of the horizons of black holes and the Universe in DSBHMG,and furthermore obtain the electric charge Q when the two horizons show the same radioactive temperature.In Sec.3,taking the correlation between the two horizons into consideration,we will present the equivalent thermodynamic quantities of DSBHMG satisfying the first thermodynamic law,and perform a quantitative analysis of the corresponding effective temperature and pressure.Finally,the main conclusions are summarized in Sec.4.Throughout the paper we use the units G=~=kB=c=1.

2 Thermodynamics of Black Holes in Massive Gravity

In the framework of(3+1)-dimensional massive gravity with a Maxwell field(denoting Fµνas the Maxwell field-strength tensor),the corresponding action always expresses as[34−37]

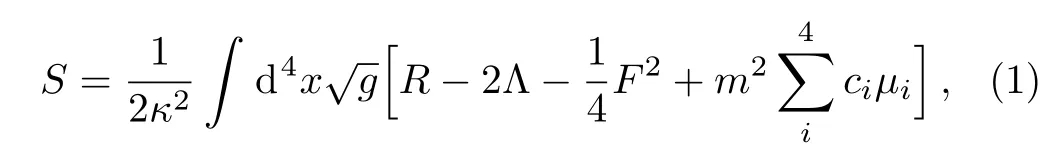
where Λ is the cosmological constant,g and R are respectively the determinant of the metric and the Ricci scalar.The last term in the right hand side denotes the massive potential associate with graviton mass m,whereµiare symmetric polynomials of the eigenvalues representing the contribution of the matrixwith fixed symmetric tensor fµν.Generated form the above action,the space-time metric of static black holes(denoting hijas Einstein space with constant curvature)can be written as

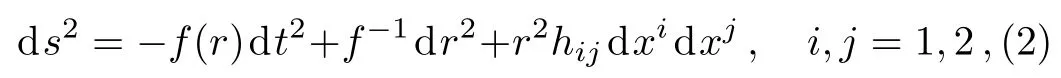
with the metric function expressed as[38−39]

Here k=+1,0,−1 respectively correspond to the sphere,Ricci flat,and hyperbolic symmetric cases.Note that the positions of black hole horizon r+and cosmic horizon rcare determined when f(r+,C)=0.

In Fig.1 we display the behavior of the metric function f(r),where the parameters are chosen as Λ=1,m0=30,m=2.12,c1=2,c2=3.18,q=1.7,while k is fixed at 1,0,and−1.It is obvious that there are two intersection points between f(r)and the axis of r,which respectively correspond to the positions of black hole horizon r+and cosmological horizon rc.Thus,the mass m0can be expressed in terms of r+,cas

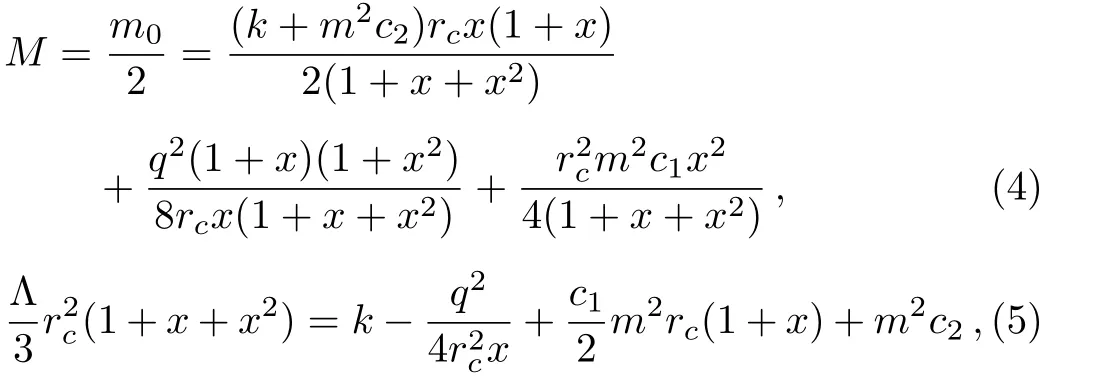
where x=r+/rc.The temperature of the black hole horizons and cosmic horizon can be written as[40]

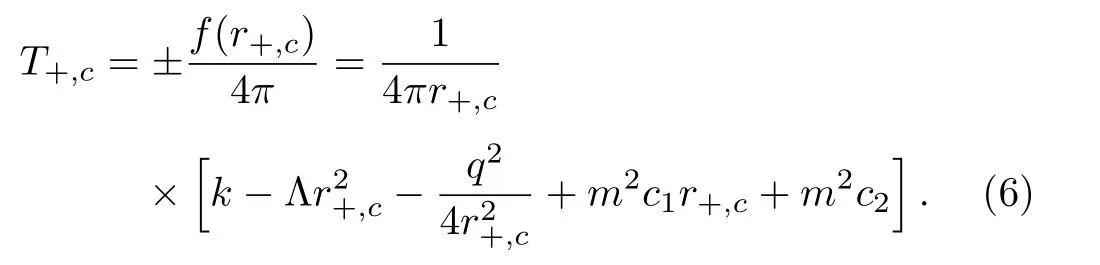
Turning to the contribution of the electrical charge q,it will also generate a chemical potential as

According to the Hamiltonian approach,we have the mass M and electric charge Q as

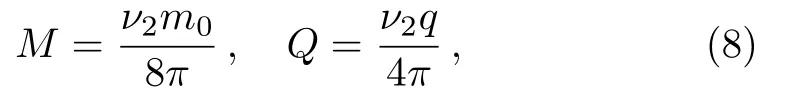
and the entropy of the two horizons respectively express as

where ν2is the area of a unit volume of constant(t,r)space(which equals to 4π for k=0).

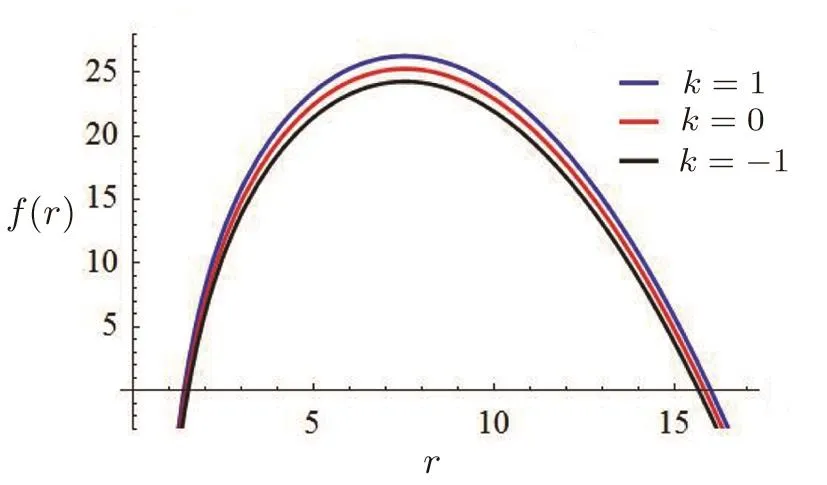
Fig.1 The metric function f(r)varying with r.

It is apparent that the thermodynamic quantities corresponding to the two horizons satisfy the first law of thermodynamics

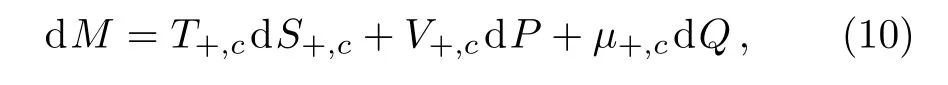
where

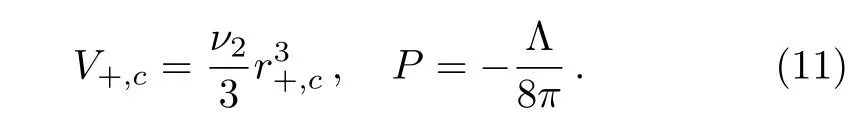
When the temperature of the black hole horizon is equal to that of the cosmological horizon,the electric charge Q and the cosmological constant Λ are related as

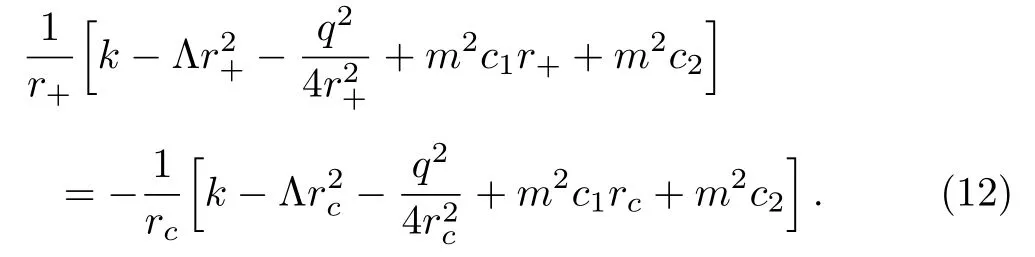
As can be seen from Eqs.(5)and(12)the electric charge of the system satisfies the following expression

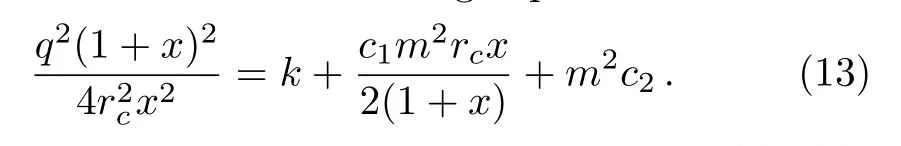
When taking T+=Tc,the combination of Eqs.(5),(6),and(13)will lead to the temperature T as

3 Effective Thermodynamic Quantities

Considering the connection between the black hole horizon and the cosmological horizon,we can derive the effective thermodynamic quantities and corresponding first law of black hole thermodynamics as

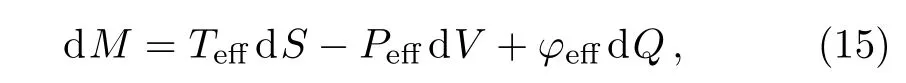
where the thermodynamic volume is defined by[3,5−6,41]

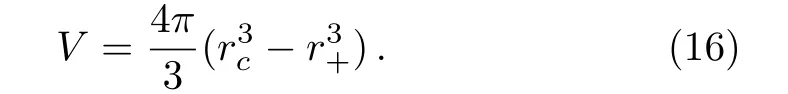
It is obvious that there exit three real roots for the equation f(r)=0:the cosmological horizon(CEH)r=rc,the inner(Cauchy)horizon of black holes,and the outer horizon(BEH)r=r+of black holes.Moreover,the de Sitter space-time is characterized by Λ >0,while Λ <0 denotes the anti-de Sitter scenario.

Here the undefined function f(x)represents the extra contribution from the correlations of the two horizons.We remark here that,when the black hole horizon and the cosmological horizon are treated as one thermodynamic system,the function f(x)could quantify the corresponding correction in the total entropy of the system.From Eq.(15),we can obtain the effective temperature Teffand pressure Peff

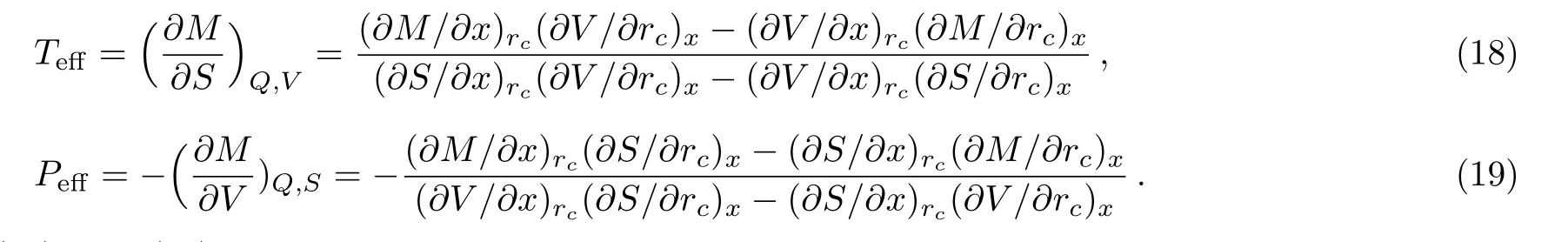
Combining Eqs.(4),(16),and(17),one can obtain

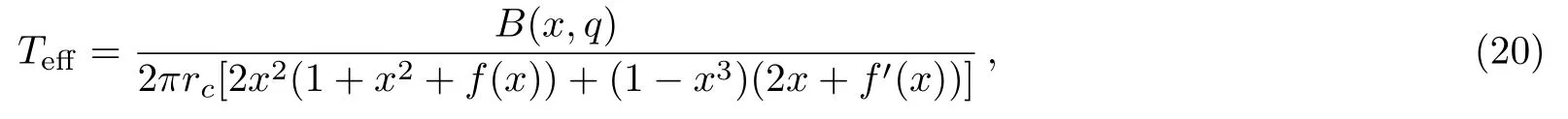
where

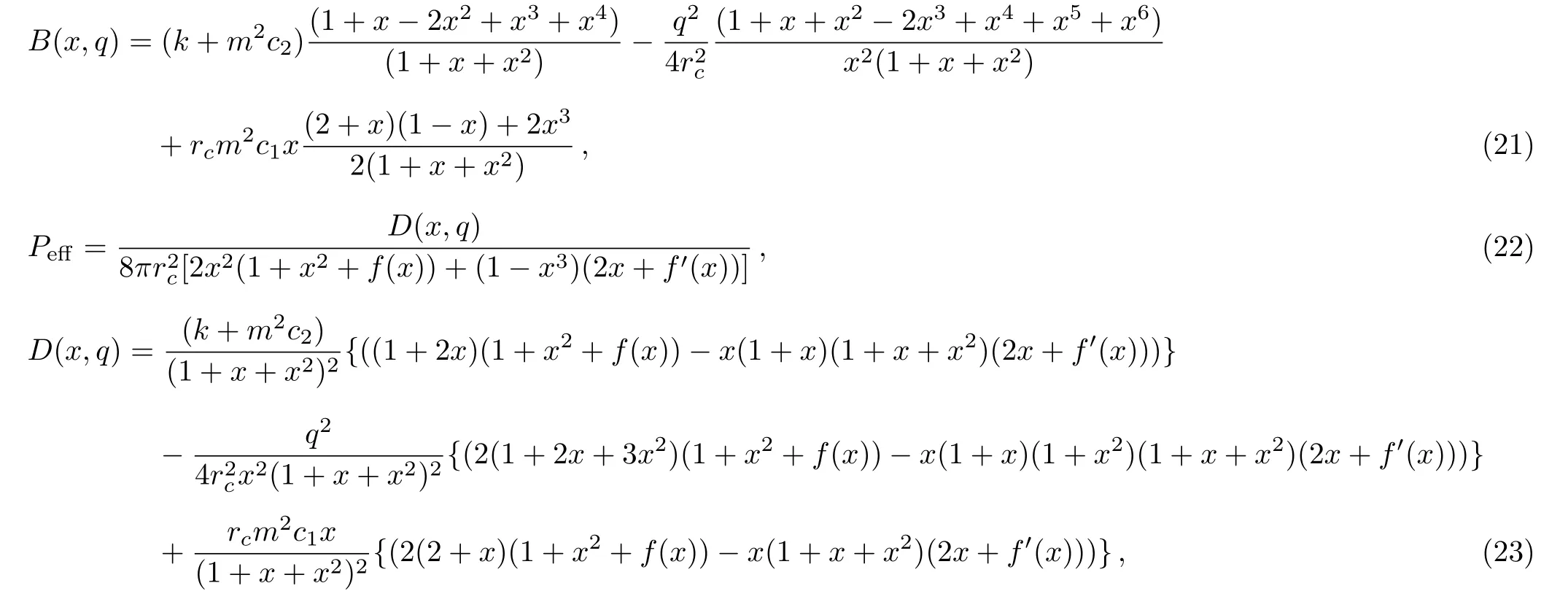
When the temperature of the black hole horizon is equal to that of the cosmological horizon,the effective temperature of the space-time should be

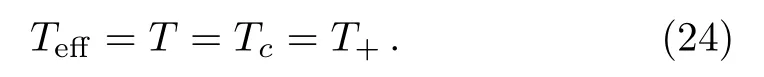
Then substituting Eq.(14)into Eq.(20),we get

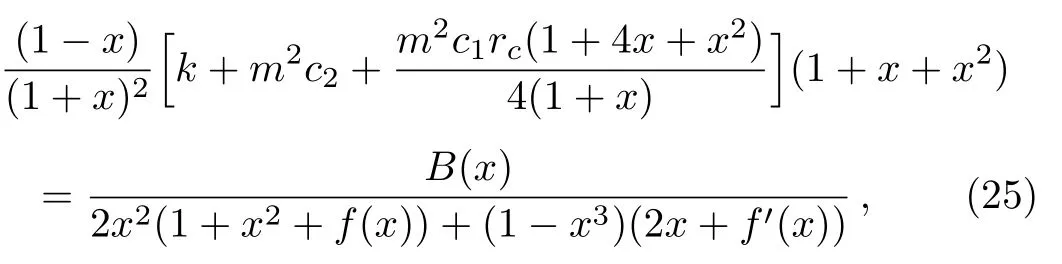
where

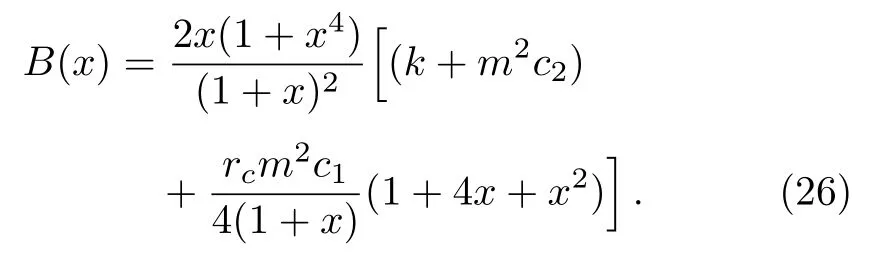
Then Eq.(25)will transform into

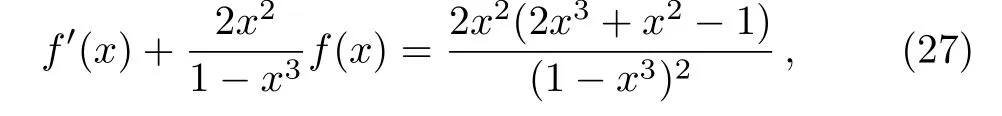
with the corresponding solution as

主动脉-二尖瓣结合部(aortomitral continuity，AMC)，为左冠状动脉窦及二尖瓣前叶之间的三角纤维区域，属于summit区域。AMC起源室早最具特征性的心电图表现是V1导联呈qR型，原因在于该位置的初始除极向量向左；其他心电图特征还包括V6导联呈R型，Ⅰ导联呈R或Rs型。由于AMC起源室早的具体起源部位和范围的差异，室早有时表现为胸前导联QRS主波呈一致正向的右束支阻滞图形；V6导联无S波，而没有前述典型的图形表现。

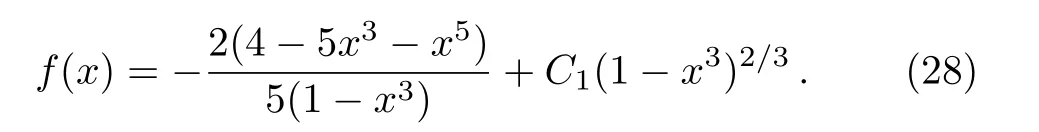
Considering the initial condition of f(0)=0,we can obtain

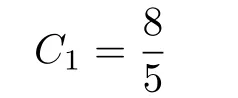
and inserting Eq.(25)into Eqs.(20)and(22)will lead to

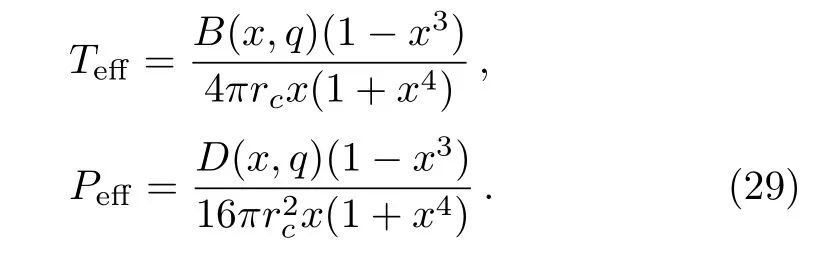
Moreover,the effective chemical potential in the first law of black hole thermodynamics can be rewritten as

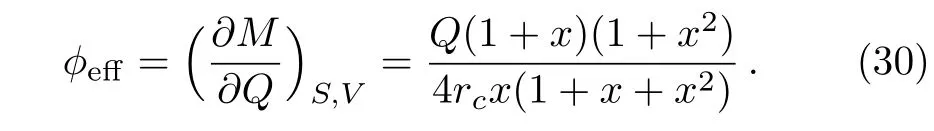
One could note that the effective chemical potential,ϕeff,is not directly related to m2c1and m2c2,which was noted in the previous work discussing the entropy of RNdS black hole.[33]Based on the above equations,the Peff-x and Teffx diagrams could be derived by taking different value of k,q,m,c1,and c2(when taking rc=1).

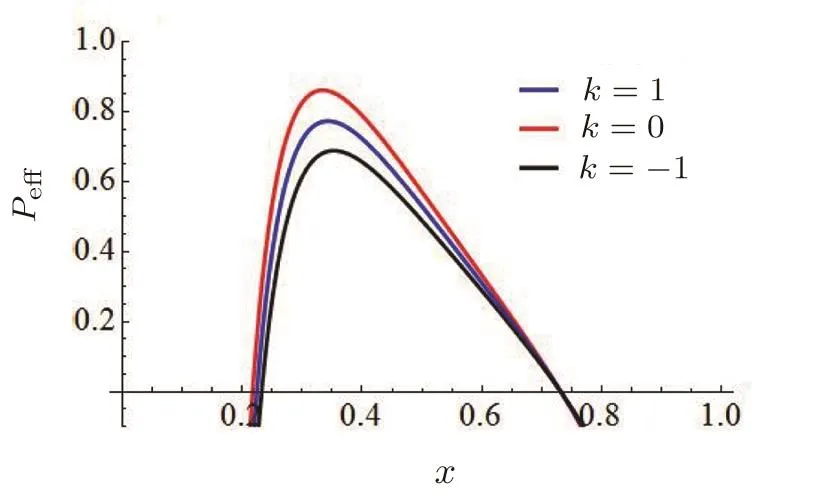
Fig.2 The Pe ff-x diagram when the parameter k is fixed at 1,0 and−1,respectively.The other parameters are fixed at m=2.12,c1=2,c2=3.18,q=1.7.

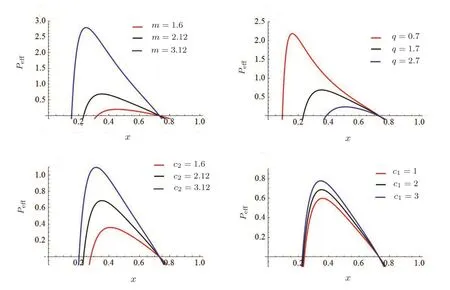
Fig.3 The Pe ff-x diagram varying with the parameters of m,c1,c2,and q,while the other two parameters are fixed at k=−1,rc=1.

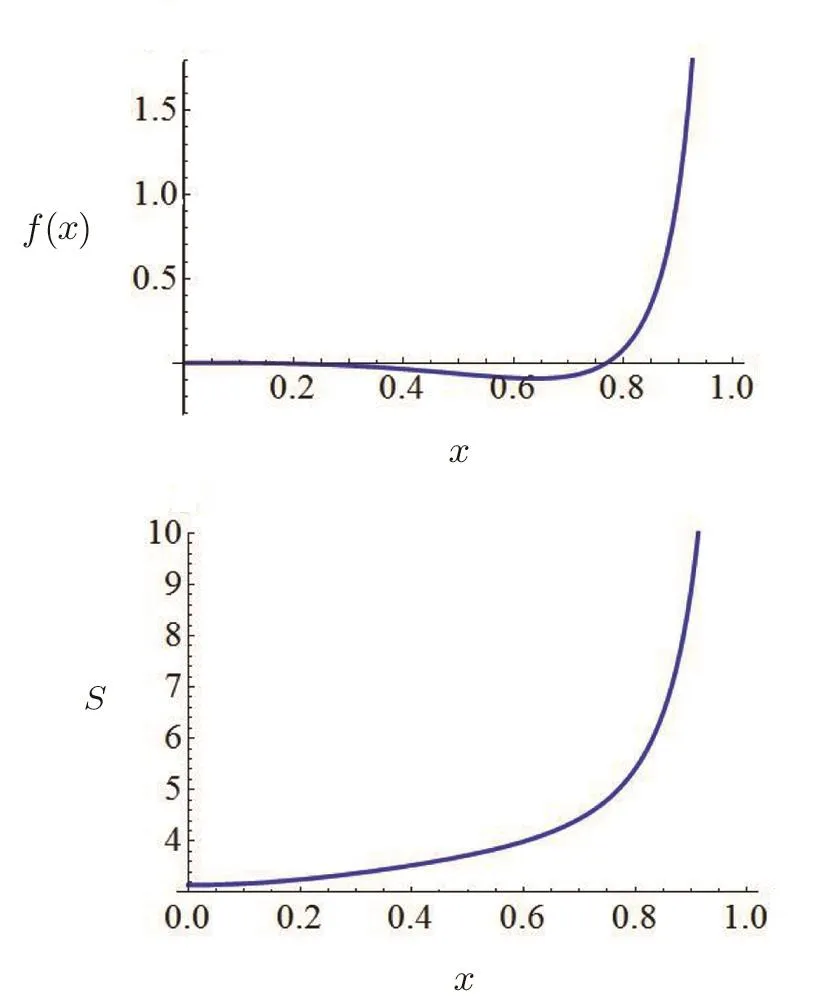
Fig.4 The S(x)-x and f(x)-x diagrams with rc=1.

In Figs.2 and 3,we illustrate an example of the Peff-x diagram with different value of relevant parameters,from which one could clearly see the effect of these parameters on the effective pressure of RN-dSQ space-time.Following the same procedure by inserting Eq.(28)into Eq.(17),we can also obtain the S(x)-x and f(x)-x diagrams with rc=1,which are explicitly shown in Fig.4.Similarly,in Figs.5 and 6,we show the evolution of the Teff-x diagram with different value of relevant parameters,from which one could perceive the effect of these parameters on the effective temperature of RN-dSQ space-time.As can be seen from Eq.(29),the special term m2c1and m2c2included in the expression of Teffand Peff,could have significant effects in the evolution of the globally effective temperature and pressure.More specifically,it is shown in Figs.3 and 6 that,the space-time considered in our analysis will recover to the well-known RNdS spacetime when m2c1and m2c2approach zero.Such conclusion is well consistent with that obtained in the previous literature.[33]

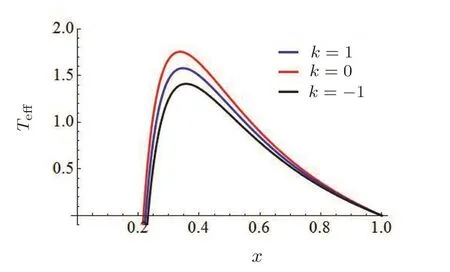
Fig.6 The Te ff-x diagram varying with the parameters of m,c1,c2and q,while the other two parameters are fixed at k=−1,rc=1.

Table 1 Summary of the highest effective temperature and the corresponding xcfor different curves in Fig.5.The value of x0when the effective temperature reaches zero is also listed.

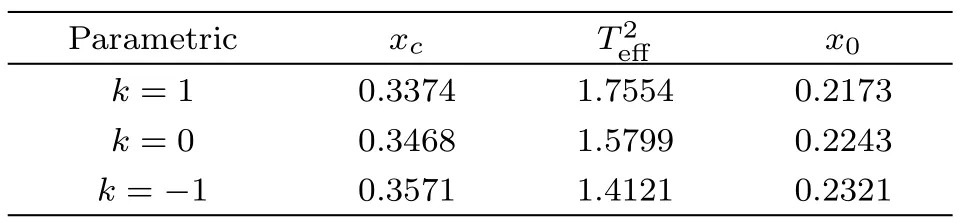
Table 1 Summary of the highest effective temperature and the corresponding xcfor different curves in Fig.5.The value of x0when the effective temperature reaches zero is also listed.

Parametric xc T2e ff x 0 k=1 0.3374 1.7554 0.2173 k=0 0.3468 1.5799 0.2243 k=−1 0.3571 1.4121 0.2321

Table 2 Summary of the highest effective temperature and the corresponding xcfor different curves in Fig.6.The value of x0when the effective temperature reaches zero is also listed.

Table 2 Summary of the highest effective temperature and the corresponding xcfor different curves in Fig.6.The value of x0when the effective temperature reaches zero is also listed.

Parametric xc T2e ff x0 q=1.0 0.222 69 2.922 26 0.134 98 k=−1 q=1.7 0.357 10 1.412 10 0.232 10 q=2.7 0.531 08 0.568 70 0.380 43 m=1.6 0.465 46 0.439 60 0.321 08 k=−1 m=2.12 0.357 10 1.412 10 0.223 10 m=3.12 0.249 46 5.611 53 0.153 24 c1=1.0 0.363 73 1.231 66 0.238 98 k=−1 c1=2.0 0.357 10 1.412 10 0.232 10 c1=3.0 0.351 14 1.595 04 0.225 99 c2=2.18 0.417 92 0.757 68 0.279 26 k=−1 c2=3.18 0.357 10 1.412 10 0.232 10 c2=4.18 0.316 77 2.224 55 0.202 18

4 Conclusion and Discussion

In this paper,by taking de Sitter space-time as a thermodynamic system,we study the effective thermodynamic quantities of de Sitter black holes in massive gravity,and furthermore obtain the effective thermodynamic quantities of the space-time.Here we summarize our main conclusions in more detail:

(i)In the previous analysis without considering the correlation between the black hole horizon and the cosmological horizon,i.e.,the two horizons are always treated as independent thermodynamic systems with different temperature,the space-time does not satisfy the requirement of thermodynamic stability.In this paper,we find that the establishment of the correlation between the two horizons will generate the common effective temperature Teff,which may represent the most typical thermodynamic feature of RN-dSQ space-time.

(ii)As can be clearly seen from the S(x)-x and Teff-x diagrams,RN-dSQ space-time in unstable under the condition of x>xcand x

(iii)We find that the interaction term f(x)in the entropy of RN-dSQ space-time takes the same form of that in RN-dS space-time.Considering that the entropy in the two types of space-time is the function of the position of the horizon,which has no relation with other parameters including the electric charge(Q)and the constant(Λ),the entropy in the two types of space-time should take the same form.This finding may contribute to the deep understanding the universal thermodynamic characteristics of de Sitter space-time in the future.

Acknowledgments

The authors declare that there is no conflict of interest regarding the publication of this paper.

[1]R.G.Cai,Nucl.Phys.B 628(2002)375

[2]B.D.Koberlein and R.L.Mallett,Phys.Rev.D 49(1994)5111

[3]B.P.Dolan,D.Kastor,D.Kubiznak,et al.,Phys.Rev.D 87(2013)104017.

[4]Y.Sekiwa,Phys.Rev.D 73(2006)084009.

[5]D.Kubiznak and F.Simovic,Class.Quant.Grav.33(2016)245001.

[6]J.McInerney,G.Satishchandran,and J.Traschen,Class.Quant.Grav.33(2016)105007.

[7]M.Urano,A.Tomimatsu,and H.Saida,Class.Quant.Grav.26(2009)105010.

[8]X.Y.Guo,H.F.Li,L.C.Zhang,and R.Zhao,Phys.Rev.D 91(2015)084009.

[9]X.Y.Guo,H.F.Li,L.C.Zhang,and R.Zhao,Class.Quant.Grav.33(2016)135004

[10]H.H.Zhao,M.S.Ma,L.C.Zhang,and R.Zhao,Phys.Rev.D 90(2014)064018.

[11]M.S.Ma,R.Zhao,and Y.Q.Ma,Gen.Relativ.Gravit.49(2017)79.

[12]T.Katsuragawa and S.Nojiri,Phys.Rev.D 91(2015)084001.

[13]F.Mellor and I.Moss,Class.Quant.Grav.6(1989)1379.

[14]D.Kastor and J.Traschen,Phys.Rev.D 47(1993)5370.

[15]H.F.Li,M.S.Ma,and Y.Q.Ma,Mod.Phys.Lett.A 32(2017)1750017.

[16]M.Azreg-A¨ınou,Phys.Rev.D 91(2015)064049.

[17]M.Azreg-A¨ınou,Eur.Phys.J.C 75(2015)34.

[18]K.Hinterbichler,Rev.Mod.Phys.84(2012)671.

[19]M.Fierz,Helv.Phys.Acta.12(1939)3.

[20]M.Fierz and W.Pauli,Proc.R.Soc.A 173(1939)211.

[21]H.V.Dam and M.J.G.Veltman,Nucl.Phys.B 22(1970)397.

[22]V.I.Zakharov,JETP Lett.12(1970)312.

[23]D.G.Boulware and S.Deser,Phys.Rev.D 6(1972)3368.

[24]D.G.Boulware and S.Deser,Phys.Lett.B 40(1972)227.

[25]C.de Rham and G.Gabadadze,Phys.Rev.D 82(2010)044020.

[26]C.de Rham,G.Gabadadze,and A.J.Tolley,Phys.Rev.Lett.106(2011)231101.

[27]S.H.Hendi,S.Panahiyan,S.Upadhyay,and B.E.Panah,J.High Energy Phys.11(2015)157.

[28]S.H.Hendi,B.Eslam Panah,and S.Panahiyan,J.High Energy Phys.05(2016)029.

[29]B.R.Majhi and S.Samanta,arXiv:gr-qc/1609.06224

[30]R.G.Cai,Y.P.Hu,Q.Y.Pan,and Y.L.Zhang,Phys.Rev.D 91(2015)024032.

[31]J.Xu,L.M.Cao,and Y.P.Hu,Phys.Rev.D 91(2015)124033.

[32]M.Cvetic,G.W.Gibbons,D.Kubiznak,and C.N.Pope,Phys.Rev.D 84(2011)024037.

[33]L.C.Zhang,R.Zhao,and M.S.Ma,Phys.Lett.B 761(2016)74.

[34]M.S.Ma,R.Zhao,and Y.S.Liu,Class.Quan.Grav.34(2017)165009.

[35]M.S.Ma and R.H.Wang,Phys.Rev.D 96(2017)024052.

[36]S.Upadhyay,B.Pourhassan,and H.Farahani,Phys.Rev.D 95(2017)106014.

[37]H.F.Li,M.S.Ma,L.C.Zhang,and R.Zhao,Nucl.Phys.B 920(2017)211.

[38]S.F.Hassan and R.A.Rosen,J.High Energy Phys.07(2011)009.

[39]A.Adams,D.A.Roberts,and O.Saremi,Phys.Rev.D 91(2015)046003.

[40]A.Dehyadegari,M.Kord Zangeneh,and A.Sheykhi,arXiv:hep-th/1703.00975.

[41]D.C.Zou,R.H.Yue,and M.Zhang,Eur.Phys.J.C 77(2017)256.

[42]P.Boonserm,T.Ngampitipan,and P.Wongjun,arXiv:grqc/1705.03278.

[43]S.H.Hendi,R.B.Mann,S.Panahiyan,and B.Eslam Panah,Phys.Rev.D 95(2017)021501.