Electrical Properties of an m×n Hammock Network∗

Zhen Tan(谭震),Zhi-Zhong Tan(谭志中), and Ling Zhou(周玲)

1School of Electronics and Information,Nantong University,Nantong 226019,China

2Department of Physics,Nantong University,Nantong 226019,China

Electric circuit theory has become the basic theory of modern electronic science and automation industry,which if rst studied by Kirchho ff[1]more than 170 years ago,is the calculation of effective resistances in the resistor networks.The development of natural science raises many complex new problems and requires people to fi nd the basic method to resolve them.It was found that many problems could be resolved by building a resistor network model.Nowadays,the resistor networks can not only be used in electrical field but also in non-electrical systems,and the numerical analysis and simulation research by modeling resistor network has become a good technique to work out a series of complicated problems.[2−3]

The main problem studied in the resistor network model is the calculation of effective resistance and node potential. Researchers have made great progress in the field of resistor networks,and made a lot of applications. Such as,classical transport,[2]electromigration phenomena,[3]lattice Greens functions,[4]graph theory,[5]resistance distance,[6]infinite network,[7−8]finite network,[9]and impedance network,[10]corner-to-corner resistance,[11−12]and so on.As you know,the calculation of node potential is relevant to many important problems,such as the transmission line,electrostatic field,IC design,and Laplace equation.In real life,the two-dimensional difference equations are common problems,such as the second order discrete equationis called Poisson equation,when kx the equation reduces to the discrete Laplace equationThese

1 Introduction

questions may be resolved by modelling resistor networks.Thus,many practical problems of calculation of potential can be resolved by modelling resistor network.[13−14]In fact,the Laplace equation is important in many fields of science and physics,which involves multiple disciplines such as electromagnetism,astronomy,and fl uid dynamics,and heat conduction,and so on.

Reviewing the history of resistor networks,we find that several good methods for calculating the effective resistance of resistor networks have been found.Such as Cserti[7]and Giordano[8]derived the resistance formulae of the infinite network by the Green function technique,Wu[9]formulated a different approach by Laplacian matrix,and derived the explicit expressions for the resistance in both finite and infinite lattices.Later the Laplacian method extended to the complex impedance network,[10]and to the network with zero resistor boundary[15−17]and to the other resistor networks.[18−19]In recent years,a new Recursion-Transform(RT)method was proposed by Tan,[20−22]which is different from the Laplacian method since the RT method just depends on one matrix along one directions(Wu’s method needs two matrices along two directions).With the applications of the RT method,many resistance formulae were discovered.[21−33]

According to the above analysis the computation of effective resistance have made great progress.However,the calculation of the nodal potential has been a difficult problem and does not be resolved until the recent research of literature,[34]which gives the precise potential formulae of the fan and cobweb networks by the RT method with potential parameters for the first time.Due to the complex structure of the resistor networks,there are still many potential of the resistor networks needs to derive.As a summary,the RT method includes two types,namely RT-I method and RT-V method,where the RT-I method is shorthand for the recursion-transform method with current parameters,[20−22]and the RT-V method is shorthand for the recursion-transform method with potential parameters.[34]Reference[28]had ever calculated the effective resistance of the hammock network as shown in Fig.1,but the electric potential of the hammock network has not been resolved before.In this paper we are going to study the electrical properties(involves potential formula,branch currents,and equivalent resistance)of the arbitrary hammock network by the RT-I method,and made a new research progress.

2 Potential Formula of Hammock Network

We study an arbitrary m×n hammock network as shown in Fig.1,where r0and r are the resistors along vertical and horizontal directions,and m and n are,respectively,the numbers of resistors along vertical and horizontal directions.Assuming the pole O is the origin of coordinate system,and the Y axis is selected on the left edge.Using coordinate{x,y}to denote nodes of the network,and denote potential function of node d(x,y)by Um×n(x,y).

Fig.1 A 7×8 hammock network in which 7 and 8 are the resistor numbers along the vertical and horizontal directions.Resistors in the vertical and horizontal directions are,respectively,r0and r.

Theorem:Assuming the current J goes from d1(x1,y1)to d2(x2,y2),and selecting the reference potential Um×n(0,0)=0,the potential of node d(x,y)in the m×n hammock network is

where we define

with b=r/r0.

In particular,when n→∞but m is finite,Fig.1 is called a semi-infinite network,the potential formula of node d(x,y)in the m×n hammock network can be written as

Equations(1)and(6)are the potential formulae of any point in an arbitrary hammock network,which are discovered by this paper for the first time.

3 A General Theory and Approach

3.1 A General Idea

Fig.2 Segment of resistor network with current directions and parameters.

To compute the node potential of an arbitrary node in the m×n hammock network,we inject a current J into the network at d1(x1,y1)and exit the current at d2(x2,y2).Denoting the branch currents in all segments of the network as shown in Fig.2.Assuming the branch currents passing through all n+1 column resistors of r0,respectively,areand U(0,0)=0.By Ohm’s law the potential at node d(x,y)relative to the O(0,0)can be written as

Obviously,to find the explicitis important.How to solve the branch currentis the key to the problem.We are going to resolve the question by the RT-I method.

3.2 Modelling Recurrence Relations

A segment of the hammock network is shown in Fig.2.Using Kirchho ff’s law to analyze the resistor sub-network,we can get the meshes voltage equations and the nodes current equations.Thus,we obtain the following equation of only containing current parameters along vertical direction by eliminating the current parameters along horizontal direction,

where b=r/r0.When considering the input and output of current J,Eq.(8)can be rewritten as a matrix form,

where Ikis an m×1 column matrix,

where the delta function δi,ymeans: δi,y(y=i)=1,δi,y(yi)=0,and

Next,according to the RT-I method that we need to build the equations of boundary conditions by the left and right edges.Similar to Eq.(9)to establish the constraint equation,we get

where E is the m×m identity matrix,matrix Bmis given by Eq.(12).

So far,we achieved all Eqs.(9)–(14)needed to calculate the branch current and the node potential of the m×n hammock network.However,according to the investigation,it is impossible for us to obtaindirectly by Eqs.(9)–(14).Thanks for the RT-I method was proposed,[20−22]which can solve this question indirectly.

3.3 Matrix Transform Method

By RT-I method we rebuild a new difference equation to solveindirectly.To realize the idea,we multiply Eq.(9)from the left side by an m×m undetermined square matrix Qm,yields

For making QmBm=TmQm,we must work out the eigenvalues of matrix Bm.Taking

Solving Eq.(16)we obtain the eigenvalues

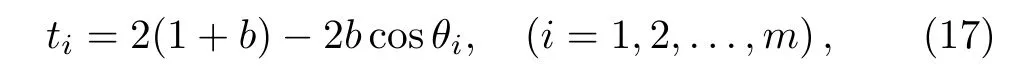
where θi=(i− 1)π/m.Thus,we can obtain the matrix of eigenvectors by following identity

where Tm=diag{t1,t2,...,tm},solving Eq.(18),we therefore obtain the eigenvectors

with the inverse matrix

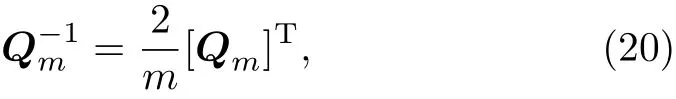
where[]Tdenotes matrix transpose.By RT-I method,we define

where Ymis an m×1 column matrix,namely

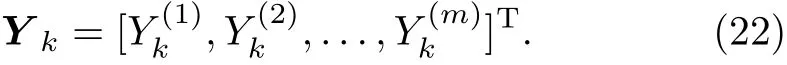
Thus,applying Eqs.(18)and(21)to(15)we therefore obtain a main equation

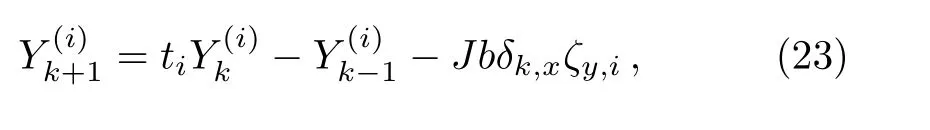
where

Next,we transform Eqs.(13)and(14)by multiplying Qmon the left-hand side,we get

At this point,we have constructed the matrix transform.Obviously,we can already resolve Eq.(23)because it has become a simple linear equation.

3.4 General Solutions of Matrix Equations

In this section,we are going to derive the exact solution ofby Eq.(23)and Eqs.(25)–(26).Assuming the λiandare the roots of the characteristic equation for Yk,we therefore obtain Eq.(5).

When i=1,there be θ1=0,from Eq.(17)we have the eigenvalue t1=2.So we need to consider the additional solution of Eq.(23).From Eq.(23)and Eqs.(25)–(26),we obtain

Using Eqs.(19)and(21),we have

According to Fig.1 and the current fluxes in all network,we have

Putting Eqs.(27)and(29)into Eq.(28)yields

When i≥2,we need to consider the piecewise solutions of Eq.(23)with the input and output of current J,we get

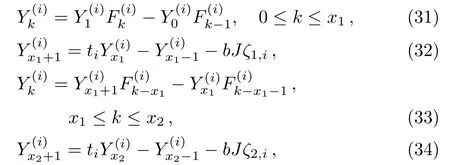
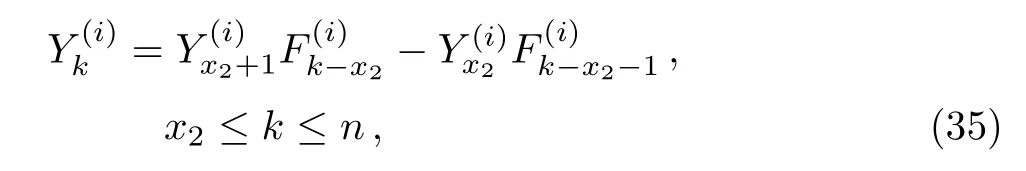
whereis defined in Eq.(3).Solving Eqs.(31)–(35)together with Eqs.(25)–(26),we get(i≥2)

whereare defined in Eqs.(3)and(4),and ζ1,i,ζ2,iare given by Eq.(24).

Thus the key parameters have been completely expressed by Eqs.(30)and(36),and Eq.(36)together with Eq.(30)are all general solutions of matrix Eqs.(23),(25),and(26).

3.5 Derivation of Potential Function

According to the require of Eq.(7),we need to derive the solutions of branch currents by using the above results.From Eq.(21),we can obtainby making use of the inverse transform matrix.Using Eqs.(19),(20),and(21)we get

Formula(37)is a key current function,in the following all the calculations will depend on this equation.Further,we obtain its summationsin Eq.(7),such as summing Eq.(37)over k from k=1 to y yields

whereis given by Eqs.(30)and(36),and the following equation is used,

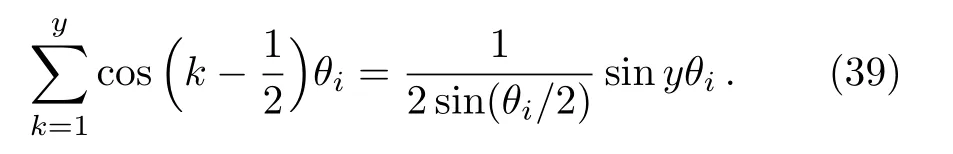
Substituting Eqs.(30)and(36)into Eq.(38),we get

whereis defined in Eq.(4).

Next,we are going to derive the potential function based on the above results.Because formula(40)is a general solution which is suitable to any conditions,thus substituting Eq.(40)into Eq.(7),we obtain

Putting Eq.(24)into Eq.(41),we therefore achieve formula(1).

In addition,we consider the condition of n → ∞ with m finite.By Eqs.(3)–(5),we get

Applying Eq.(42)to Eq.(1),we get

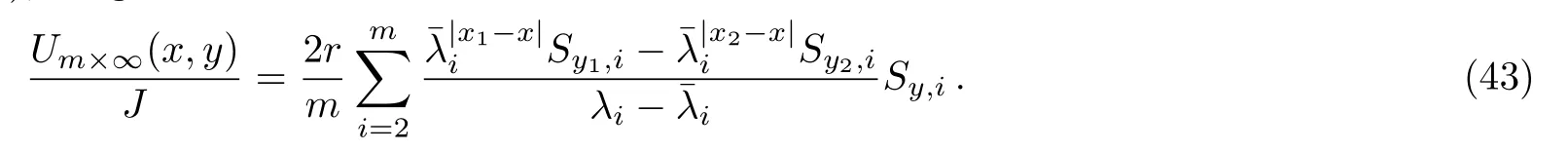
By Eq.substitute to Eq.(43)we therefore achieve Eq.(6).

So far,the main results proposed in Sec.2 have been verified.Equations(1)and(6)are discovered for the first time by this paper.

4 Applications of Potential Formula

Owing to Eq.(1)is a general potential formula of hammock network,that is to say,the parameters in formula(1)are arbitrary,we can get a series of special and interesting results when we take some special conditions in formula(1).In the following,we always assume U(0,0)=0.

Application 1 Consider an arbitrary m×n hammock network as shown in Fig.1.Assume the outputted current J meets d2(x2,y2)=O(0,0),and the current J is inputted in the network at the node d1(x1,y1),from Eq.(1)with Sy2,i=S0,i=0,the potential of node d(x,y)is

whereis defined in Eq.(4).

Application 2 Consider an arbitrary m×n hammock network of Fig.1.When inject current J at node d1(x1,y1)and exit the current J at node d2(x1,y2)(x2=x1),the potential function of node is

where Sk,iis defined in Eq.(2),and β(i)x1∨xis defined in Eq.(4).

Application 3 Consider an arbitrary m×n hammock network of Fig.1.When the current J goes from node d1(0,0)to node d2(x2,m),we have y1=0,y2=m,from Eq.(1),we have

When the current J goes from node d1(x1,m)to node d2(0,0),from Eq.(1),we get

Eqs.(46)and(47)tell us that the input and output place of current J affects the expression of the potential.

Application 4 Consider an arbitrary m×n hammock network of Fig.1.When the current J goes from node d1(x1,y1)to node d2(x2,y1),from Eq.(1)with y1=y2,the potential of node d(x,y)can be written as

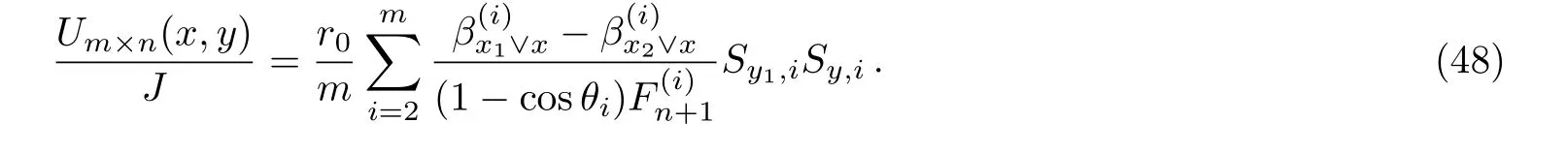
Application 5 In Fig.1,assuming the current injected at node di(xi,y1)(i=0,1,...,k)on the same horizontal axis is k/J,and the current exited from the pole O(0,0)is J.From Eq.(44),we have the potential function

In particular,if the node di(xi,y1)is evenly distributed on the same horizontal axis of the n+1 nodes,then the potential at node d(x,y)is

Proof of Eq.(50):

Due to the potential is a scalar,each current source will produce a potential independently,when the n+1 currents input to the network,any node potential is the summations of n+1 potentials.By Eq.(49)we get the potential

Next we calculate the sums of.From Eq.(4)we have)

Because xk,x are the natural numbers,and 0≤|xk−x|≤n,thus

Putting Eq.(53)into Eq.(51),we immediately obtain formula(50).

5 Resistance of Hammock Network

Consider an arbitrary m×n hammock network as shown in Fig.1.The effective resistance between d1(x1,y1)and d2(x2,y2)in an m×n hammock network can be written as

where we simply callis defined in Eq.(2).

Proof of Eq.(54):

Assuming the potentials at d1(x1,y1)and d2(x2,y2)are U(x1,y1)and U(x2,y2),using Ohm’s law we get By Eq.(1),setting(x,y)=(x1,y1)and(x,y)=(x2,y2)respectively,we get

Substituting Eqs.(56)and(57)into Eq.(55),we therefore obtain formula(54).

Please note that Ref.[28]has studied the equivalent resistance of the m×n hammock network,and gave out the formula is as Eq.(54).But our approach is based on the potential function which is different from Ref.[28].Clearly using potential function to derive the equivalent resistance is more easy than the other method.

6 Conclusion and Comment

It is important for us to search for the explicit potential formula of an arbitrary resistor network because researchers are used to simulating many problems by means of resistor network model,but it has been a difficult thing to find the potential formula of the resistor network.In this paper,we obtained a series of exact potential formulae of an m×n hammock network by the RT-I method for the first time.In academic research,from ancient to present there are only two papers proposed the precise potential formula,the first article is Ref.[34]which first find the potential formulae of the fan and cobweb networks by the RT-V method,the second article is this paper which first find the potential formula of the hammock network by the RT-I method.Please note that RT-I method is different from RT-V method because the RT-I method relies on current parameters other than the RT-V method relies on potential parameters.Thus our research is a theoretical innovation since we first use the RT-I method to compute the potential of the network.

As applications of the potential function in an arbitrary m×n hammock network,many interesting results are produced such as Eqs.(44)–(50),and naturally the equivalent resistance formula is deduced by the potential formula such as Eq.(54).A review of the Laplace method used in Ref.[28]that,when applied to the hammock network,gives the result in terms of a double summation.Compared to the actual method,the RT-I method offers a direct and somewhat simpler approach since the RT-I method applied to the hammock network gives the result in terms of a single summation,such as the results of Eqs.(1)and(54).In additional,the RT-I method can be extended to impedance networks if we replace resistors by impedances.

[1]G.Kirchho ff,Ann.Phys.Chem.148(1847)497.

[2]S.Kirkpatrick,Rev.Mod.Phys.45(1973)574.

[3]C.Pennetta,E.Al finito,L.Reggiani,et al.,Phys.Rev.B 70(2004)174305.

[4]S.Katsura and S.Inawashiro,J.Math.Phys.12(1971)1622.

[5]Woong Kook,Adv.Appl.Math.46(2011)417.

[6]D.J.Klein and M.Randi,J.Math.Chem.12(1993)8195.

[7]J.Cserti,Am.J.Phys.68(2000)896.

[8]S.Giordano,Int.J.Circ.Theor.Appl.33(2005)519.

[9]F.Y.Wu,J.Phys.A:Math.Gen.37(2004)6653.

[10]W.J.Tzeng and F.Y.Wu,J.Phys.A:Math.Gen.39(2006)8579.

[11]J.W.Essam and F.Y.Wu,J.Phys.A:Math.Theor.42(2009)025205.

[12]N.Sh.Izmailian and M.C.Huang,Phys.Rev.E 82(2010)011125.

[13]M.C.Lai and W.C.Wang,Numer.Methods Partial Differ.Equ.18(2010)56.

[14]L.Borges and P.Daripa,J.Comput.Phys.169(2001)151.

[15]N.Sh.Izmailian,R.Kenna,and F.Y.Wu,J.Phys.A:Math.Theor.47(2014)035003.

[16]N.Sh.Izmailian and R.Kenna,J.Stat.Mech.9(2014)1742.

[17]N.Sh.Izmailian and R.Kenna,Chin.J.Phys.53(2015)040703.

[18]J.H.Asad,J.Stat.Phys.150(2013)1177.

[19]J.H.Asad,Mod.Phys.Lett.B 27(2013)151350112.

[20]Z.Z.Tan,Chin.Phys.B 24(2015)020503.

[21]Z.Z.Tan,Phys.Rev.E 91(2015)052122.

[22]Z.Z.Tan,Sci.Rep.5(2015)11266.

[23]Z.Z.Tan,L.Zhou,and J.H.Yang,J.Phys.A:Math.Theor.46(2013)195202.

[24]Z.Z.Tan,J.W.Essam,and F.Y.Wu,Phys.Rev.E 90(2014)012130.

[25]J.W.Essam,Z.Z.Tan,and F.Y.Wu,Phys.Rev.E 90(2014)032130.

[26]Z.Z.Tan and J.H.Fang,Commun.Theor.Phys.63(2015)36.

[27]Z.Z.Tan,Int.J.Circ.Theor.Appl.43(2015)1687.

[28]J.W.Essam,N.S.Izmailian,R.Kenna,and Z.Z.Tan,R.Soc.Open Sci.2(2015)140420.

[29]Z.Z.Tan,Commun.Theor.Phys.67(2017)280.

[30]Z.Z.Tan and Q.H.Zhang,Acta Phys.Sin.66(2017)070501.

[31]Z.Z.Tan,Chin.Phys.B 25(2016)050504.

[32]L.Zhou,Z.Z.Tan,and Q.H.Zhang,Front.Inform.Technol.Electron.Eng.18(2017)1186.

[33]Z.Z.Tan,J.H.Asad,and M.Q.Owaidat,Int.J.Circ.Theor.Appl.45(2017)1942.

[34]Z.Z.Tan,Chin.Phys.B 26(2017)090503.