Modeling Chemically Reactive Flow of Sutterby Nano fluid by a Rotating Disk in Presence of Heat Generation/Absorption

T.Hayat,Salman Ahmad,M.Ijaz Khan,,∗and A.Alsaedi

1Department of Mathematics,Quaid-I-Azam University,Islamabad 44000,Pakistan

2Nonlinear Analysis and Applied Mathematics Research Group,Department of Mathematics,Faculty of Science,King Abdulaziz University,P.O.Box 80257,Jeddah 21589,Saudi Arabia

1 Introduction

Heat transfer has numerous applications in various fields such as heat exchangers,combustors,centrifugal and axial blades compressor,microelectronic boards circuit,gas turbines blades,computer processer,fuel cells,hybridpowered engines,refrigerators,air-conditioners,and many others.Heat transfer fl uids effectively depend on their physical characteristics such as heat capacity,density,viscosity,and thermal conductivity.The primary barrier for transfer heat is small thermal conductivity of fluids.Thus,it is necessary to make out the mechanisms through,which the thermal conductivity can be improved.An innovative procedure for increasing heat transfer through mixing ultra fine solid particles in base liquids has been extensively used.The word nano fluids is referred to these types of liquids by suspending particles(nano-scale)in the base liquids.First time the word nano fluids was developed by Choi.[1]Then Buongiorno[2]proposed a model to analyze heat transfer enhancement in the nano fluids.He studied seven slip phenomena such that Brownian diffusion,Magnus, fluid drainage,inertia,gravity,diffusiophoresis,and thermophoresis.He clarified that Brownian diffusion and thermophoresis are ruling slip phenomena in the nanoliquids.Lin et al.[3]addressed MHD in flow of pseudoplastic nanoliquids.Abbasi et al.[4]characterized flow of nano fluids past a moving sheet.Hayat et al.[5]discussed flow of silver and copper water nanoliquids with thermal radiation and nonlinear convection.Malvindi et al.[6]studied thermal characteristics in hydromagnetics Al2O3-water nanoliquids in a microannular cylinder.Shape effects of nano-scale particles in Cu-H2O nanoliquids on entropy generation are explored by Ellahi et al.[7]Effect of MHD on CuO-water nano fluids with mixed convection is examined by Shekholeslami et al.[8]Stagnation point flow of viscoelastic nanoliquid with MHD and nonlinear thermal radiation is explored by Farooq et al.[9]Hayat et al.[10]evaluated impact of Hall,heating and ion effects on the flow of Jeffrey nano fluid.

Mass and heat transfer problems with chemical reaction have a considerable attention.Mass and heat transfer effects simultaneously occurs in many processes i.e.evaporation,drying, flow in a dessert cooler,energy exchange in a cooling tower,in curing of plastic chemical processing,and cleaning of materials and manufacturing of insulated cables and pulp.Postelnicu[11]evaluated effect of chemical reaction on mass and heat transfer through convection over a vertical sheet with porous medium and Dufour and Soret effects.Rout et al.[12]studied the characteristic of chemical reaction and convective boundary constraints in flow over a vertical surface.Shehzad et al.[13]examined chemical reaction in MHD flow of nanoliquids.Raddya et al.[14]examined influence of rotation and chemical reaction in MHD flow of nanoliquids.Hayat et al.[15]explored chemical reaction in MHD flow of nano fluids.

In nature there are various materials having diverse features.Navier-Stokes theory is incapable to described these types of materials.These materials include synovial fluids,gypsum paste,printer ink,yogurt,clays,hydrogenated caster oil,drilling mud,paints,colloidal suspension,blood,toothpaste ta ff y,mayonnaise,butter,cheese,ketchup,soup,jam,shampoos etc.Therefore various models of non-Newtonian fluids are suggested(see Refs.[16–21]).Here we aim to consider Sutterby fluid model.

This attempt concentrates for Sutterby nano fluid flow due to a rotating stretchable disk. Further magnetic if eld,chemical reaction and heat source effects are evaluated.Appropriate transformation is employed to obtain the nonlinear system of ODE’s.For numerical treatment we use Built-in-Shooting method.[22−25]Influences of introduced parameters on velocity,concentration and temperature are discussed through graphs.Surface drag force,temperature gradient,and concentration gradient are numerically examined through tables.

2 Formulation

We have an interest to examine flow of Sutterby nano fluid due to rotating stretchable disk.Additionally,the magnetic field,chemical reaction and heat source effects are also considered.The disk is at z=0 and fluid occupied the region z>0(see Fig.1).Disk rotates with angular speed w around the z-axies and stretching with rate c in radial direction(r-direction).Brownian motion,thermophoresis,and chemical reaction have been considered.Heat generation/absorption is accounted.Mathematical expressions for considered problem

where u,v,and w denote velocity components,ρ density,µ dynamic viscosity,δ electric conductivity,B0strength of applied magnetic field,T temperature,cpspecific heat,τ heat capacities ratio,DBcoefficient of Brownian diffusion,DTcoefficient of thermophoretic diffusion,Q0heat absorption generation coefficient,T∞ambient temperature,C concentration,and k⋆reaction rate.

In terms of Sutterby fluid model the viscosity relation is chosen as

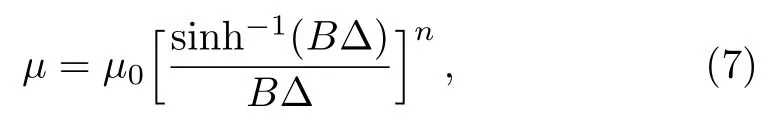
whereµ0,B,and n are positive parameters and∆ the shear rate.Parameterµ0denotes viscosity at low shear rates,B characteristic time and n dimensionless quantity.When n=0 then Sutterby model predicts viscous fluid behavior and for n=1 it reduces to Eyring model.By binomial expansion one can write

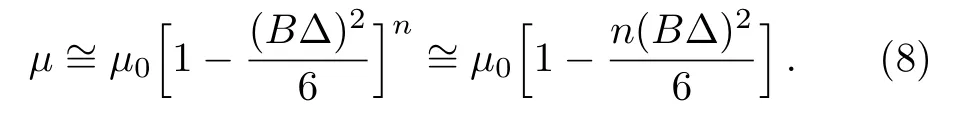
Now shear rate(∆)can be defined as

where A1is the first order Rivlin-Erickson tensor define by A1=L+LT.

Considering

continuity relation verified identically and the remaining flow expressions are

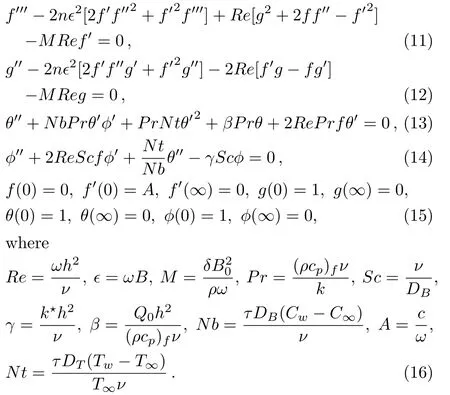
Note that Re indicates Reynolds number,ϵ material parameter,M Hartmann number(Magnetic parameter),Pr Prandt number,Sc Schmidt number,A ratio of stretching parameter,γ chemical reaction parameter,β heat source parameter to angular velocity,Nb Brownian parameter and Nt thermophoresis parameter.

Now surface drag force,temperature gradient and Sherwood number can be defined as

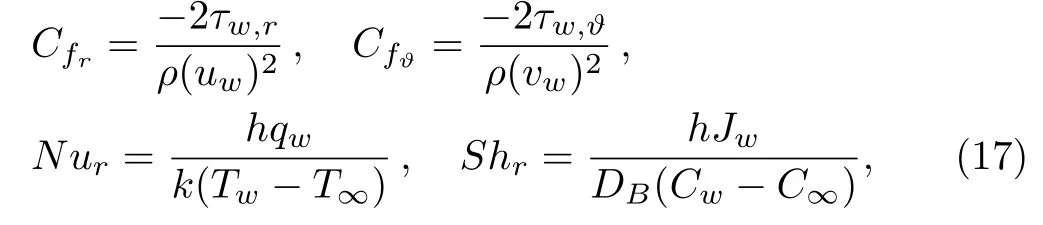
where shear stresses τw,r,τw,ϑ,mass flux Jwand heat flux qware given by

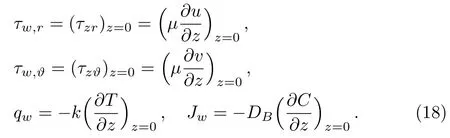
Substituting Eq.(18)in Eq.(17),we get

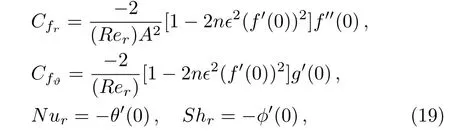
where Rer=rhω/ν indicates local Reynolds number.

3 Numerical Solution and Discussion

This section intends to compute the obtained systems numerically through Built-in-Shooting method.Here concentration,temperature and velocity are physically focussed by distinct sundry variables. Attention is particularly given to the upshots of Reynolds number(Re),material parameter(ϵ),Hartmann number(M),Schmidt number(Sc),Prandtl number(Pr),ratio parameter(A),chemical reaction parameter(γ),Brownian variable(Nb),heat source parameter(β)and thermophoresis variable(Nt).Further numerical values of surface drag force,Sherwood number and heat transfer rate are presented in Tables 1–4.

Table 1 Numerical simulation for CfrRer.

Numerical values for radial and tangential skin frictions(CfrRerand CfϑRer)with variation in different variables like dimensionless constant(n),material parameter(ϵ),Reynolds number(Re),Hartmann number(M)and stretching parameter(A)are calculated in Tables 1 and 2.Table 1 shows that surface drag force in radial direction is increased for higher estimation of Reynolds number(Re)and Hartmann number(M)while it decays for dimensionless constant(n),material parameter(ϵ)and stretching parameter(A).Table 2 demonstrates that surface drag force in tangential direction decays through increasing dimensionless constant(n),material parameter(ϵ)and stretching rate(A). On the other hand surface drag force shows increasing behavior for larger values of Reynolds number(Re)and Hartmann number(M).The effects of Brownian motion(Nb),Prandtl number(Pr),thermophoresis(Nt),heat source/sink(β),Reynolds number(Re),Schmidt number(Sc)and chemical reaction(γ)on heat transfer rate(Nur)are computed in Table 3.It is noticed that for increasing values of Brownian parameter,Prandtl number,Reynolds number,Schmidt number and chemical reaction the heat transfer coefficient enhances while it reduces for thermophoresis parameter and heat source/sink.

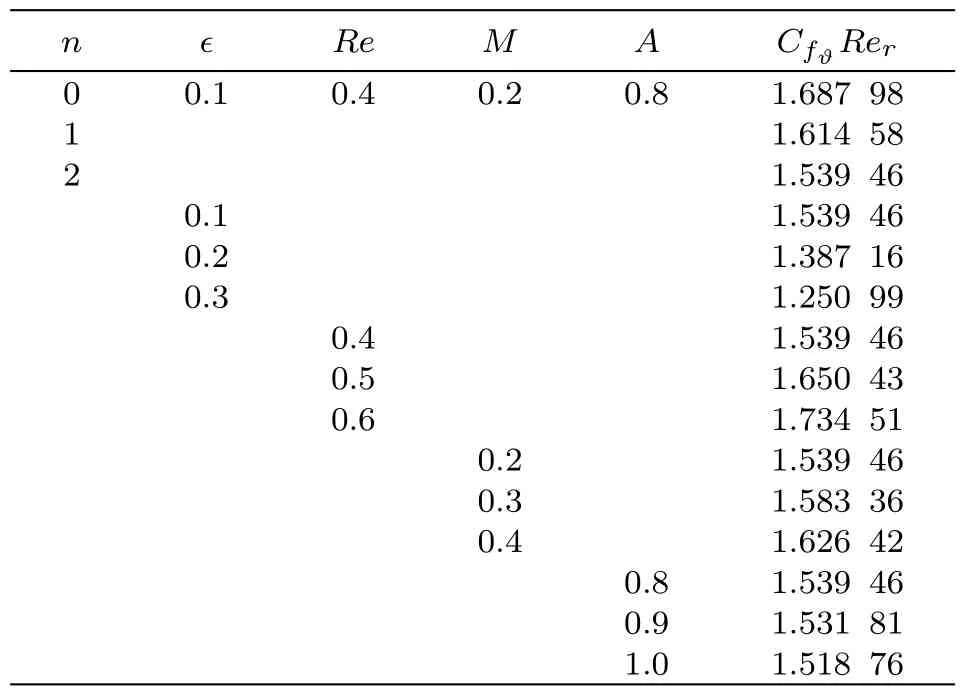
Table 2 Numerical simulation for CfϑRer.

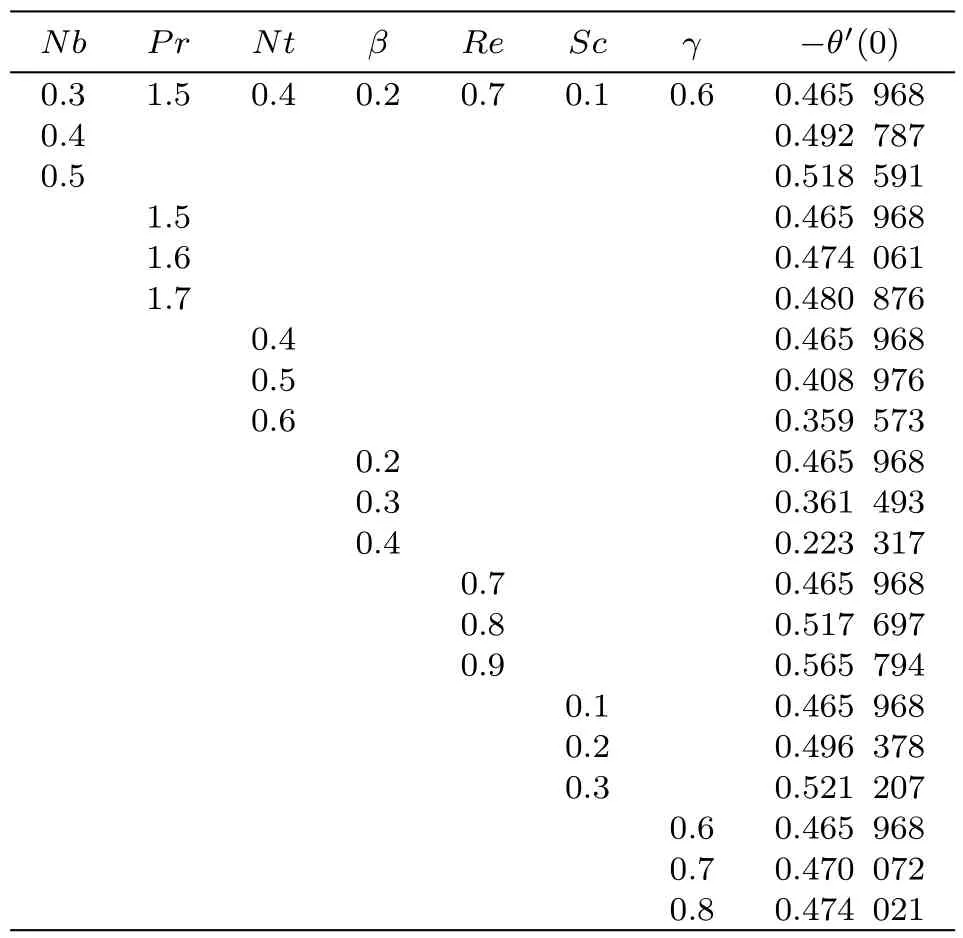
Table 3 Numerical simulation for Nur.

Table 4 shows the influences of Brownian motion(Nb),Prandtl number(Pr),thermophoresis(Nt),heat source/sink(β),Reynolds number(Re),Schmidt number(Sc)and chemical reaction(γ)on Sherwood number.Clearly for increasing values of Brownian parameter,thermophoresis parameter,heat generation/absorption,Schmidt number,Reynolds number and chemical reaction,Sherwood number enhanced and it is reduced with Prandtl number.

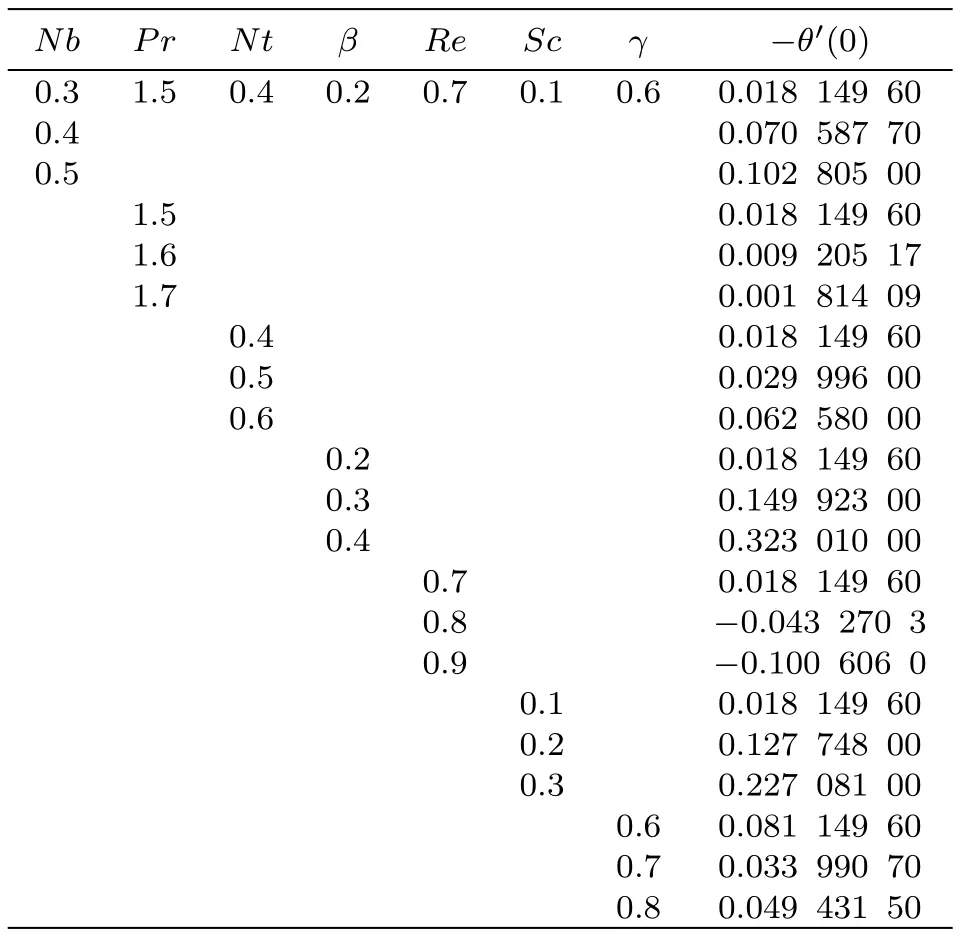
Table 4 Numerical simulation for Shr.

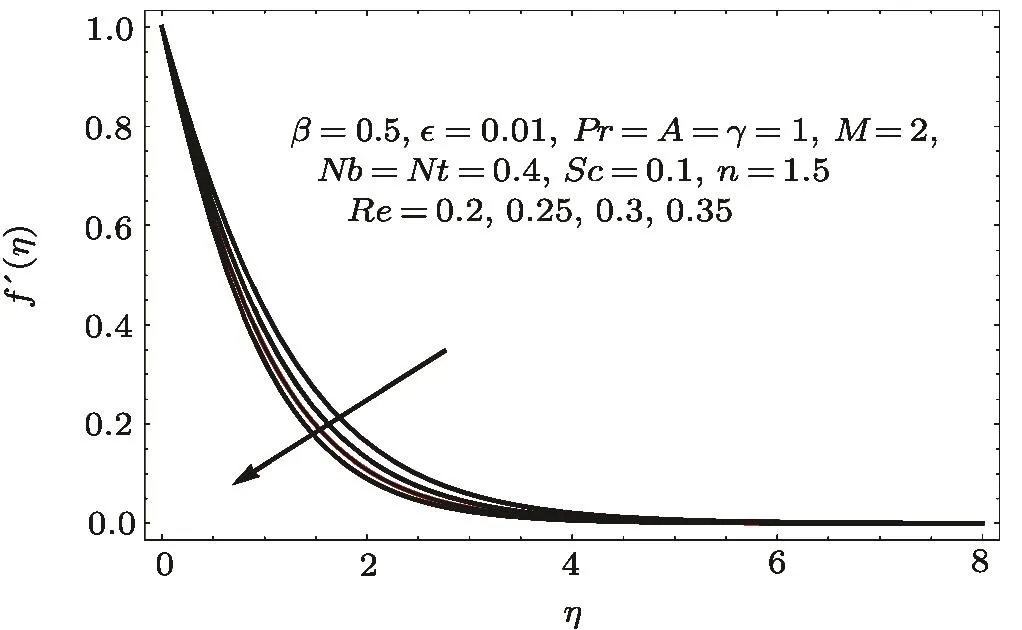
Fig.2 f′(η)variation for Re.

Figures 2–16 describe the impacts of Reynolds number(Re),dimensionless positive constant(n),material parameter(ϵ),Hartmann number(M)and stretching parameter(A)on radial velocity(f′(η)),axial velocity(f(η))and tangential velocity(g(η)).Figures 2–4 show that radial f′(η),axial f(η),and tangential g(η)velocities are decreasing functions of Re.Here Re is increasing function of angular speed ω,which yields decrease in velocities.Figures 5–7 sketch the behaviors of radial f′(η),axial f(η),and tangential g(η)velocities through variation in n.Clearly velocities(axial,radial,tangential)are reduced by n.Effects of M on f′(η),f(η),and g(η)are portrayed in Figures 8–10.It is noted that velocities(f′(η),f(η),g(η))decay with variation in M.Since M is directly proportional to resistive force known as Lorentz force,which opposes the fluid motion so f′(η),f(η)and g(η)decay.Figures 11–13 depict the influences of ϵ on radial,axial and tangential pro files.Increasing values of material parameter ϵ decrease f′(η),f(η)and g(η)velocities.Physically for larger values of material parameter the characteristic time is higher for fl uid and thus reduction occurs in velocities.

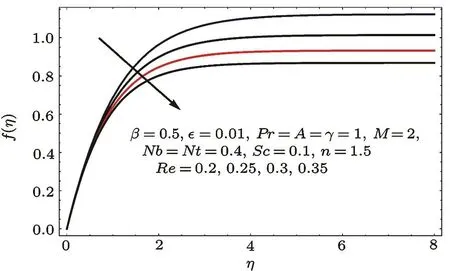
Fig.3 f(η)variation for Re.

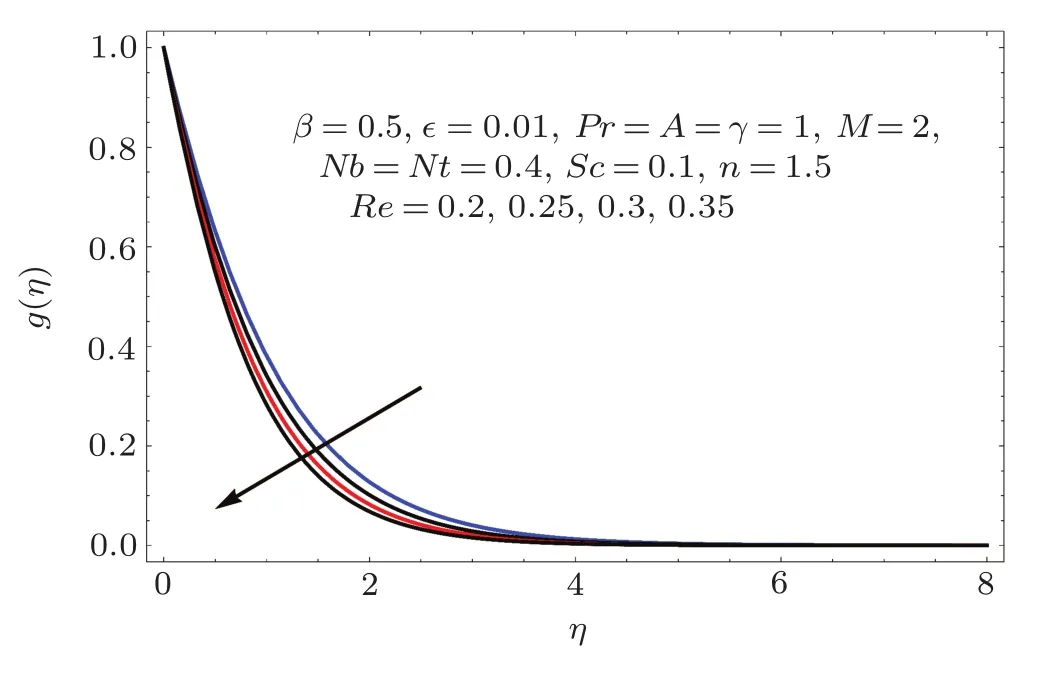
Fig.4 E ff ect of Re on g(η).

Fig.5 f′(η)variation for n.

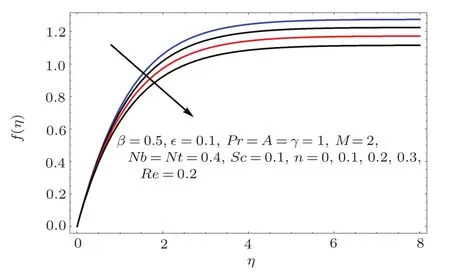
Fig.6 f(η)variation for n.

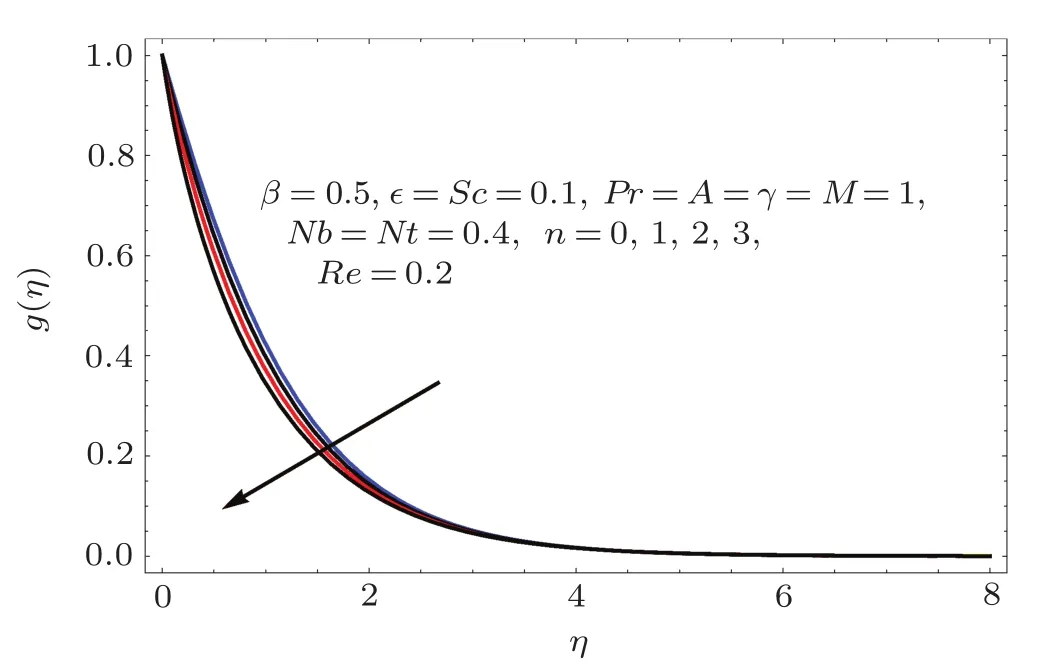
Fig.7 E ff ect of n on g(η).

Fig.8 f′(η)variation for M.

Figures 14–16 are portrayed to show the influences of parameter A on axial,radial and tangential velocities.For larger A the axial and radial velocities are increasing.It is due to an increase in stretching rate.However tangential velocity decays for larger A.Physically stretching parameter(A)is the ratio of stretching rate(c)and angular speed(ω).For larger values of stretching parameter the stretching rate dominates over angular speed and therefore the axial while radial velocities enhanced and tangential velocity reduced.

Fig.9 f(η)variation for M.

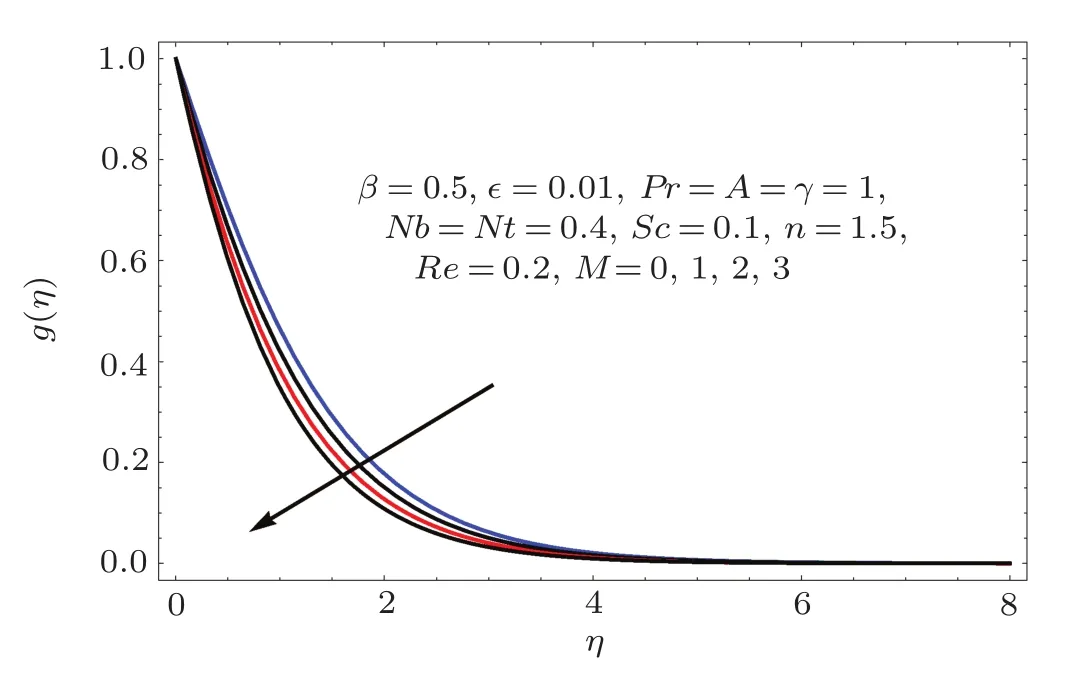
Fig.1 0 g(η)variation for M.

Figures 17–21 captured the influences of Prandtl number(Pr),thermophoresis variable(Nt),Reynolds number(Re),Brownian variables(Nb)and heat source parameter(β)on temperature distribution(θ(η)).Figure 17 illustrates the effect of Prandtl number(Pr)on θ(η).Clearly θ(η)is reduced for higher estimations of Pr.Physically Prandtl number(Pr)is ratio of momentum diffusivity to thermal diffusivity.Thermal diffusivity is predominant for higher values of Prandtl number and so temperature decays.Impact of Nt on θ(η)is portrayed in Fig.18.It is noticed that θ(η)enhanced through larger Nt.Larger estimation of Nt correspond to stronger thermophoretic force and nanoparticales move from warm to cold regions.Therefore temperature field grows.Figure 19 depicts behavior of Reynolds number(Re)on θ(η).Here θ(η)decays for larger estimation of Re.Figure 20 captured variation of Nb for θ(η).For increasing values of Nb the temperature decreases.Effect of heat source(β)on θ(η)is examined in Fig.21.Clearly temperature(θ(η))is enhanced via β.

Figures 22–26 demonstrate the effects of Schmidt number(Sc),Reynolds number(Re),Brownian parameter(Nb),thermophoresis parameter(Nt)and chemical reaction(γ)on concentration ϕ(η).

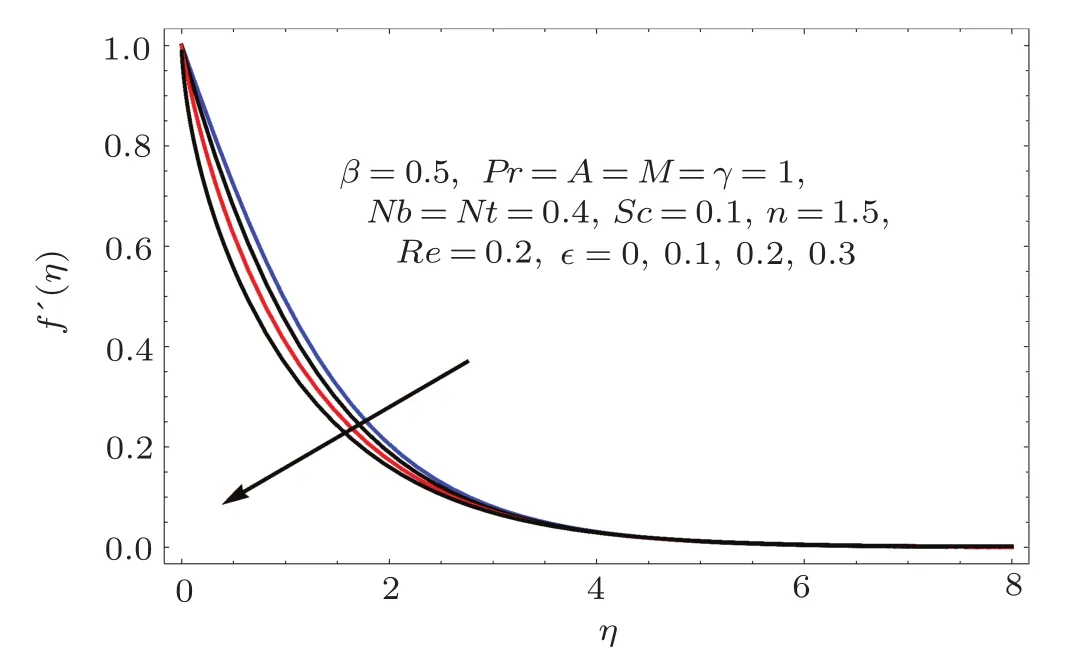
Fig.1 1 f′(η)variation for ϵ.

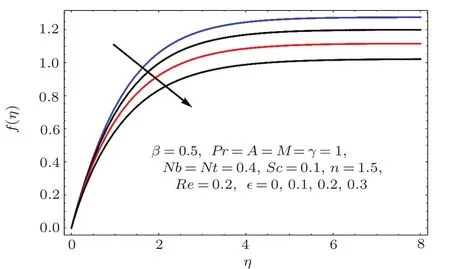
Fig.1 2 Effect of ϵ on f(η).

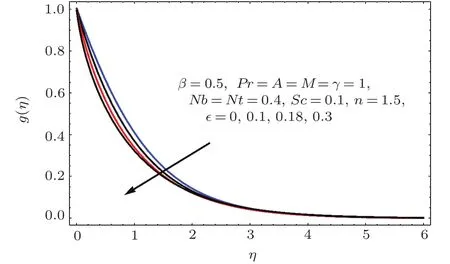
Fig.1 3 g(η)variation for ϵ.

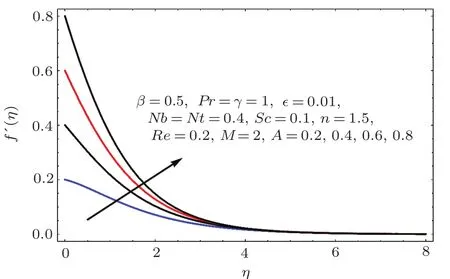
Fig.1 4 f′(η)variation for A.

Fig.1 5 Behavior of A on f(η).

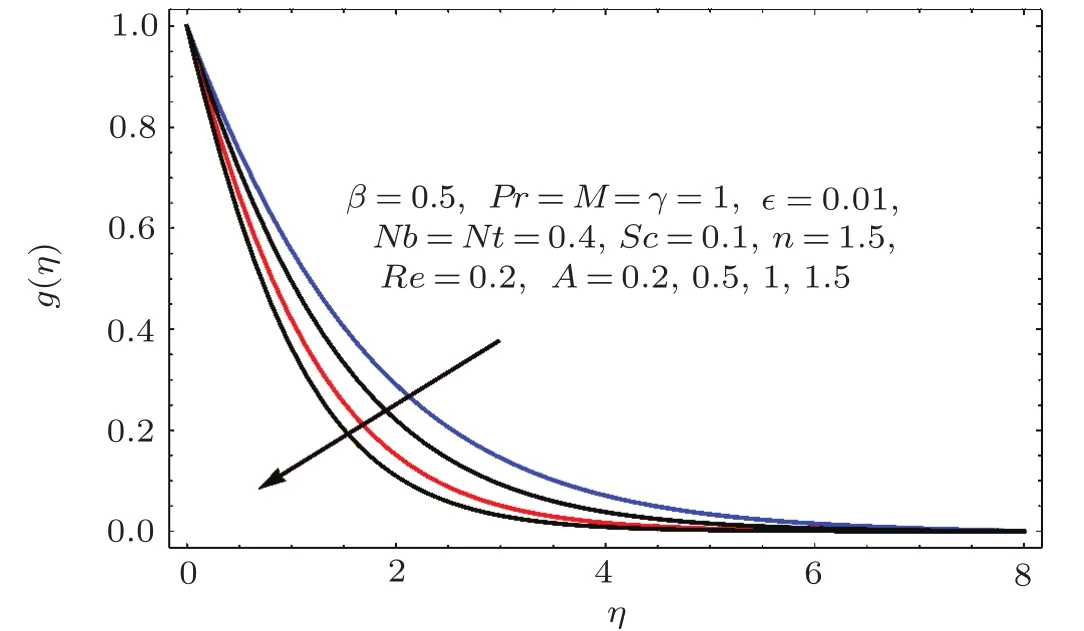
Fig.1 6 Effect of A on g(η).

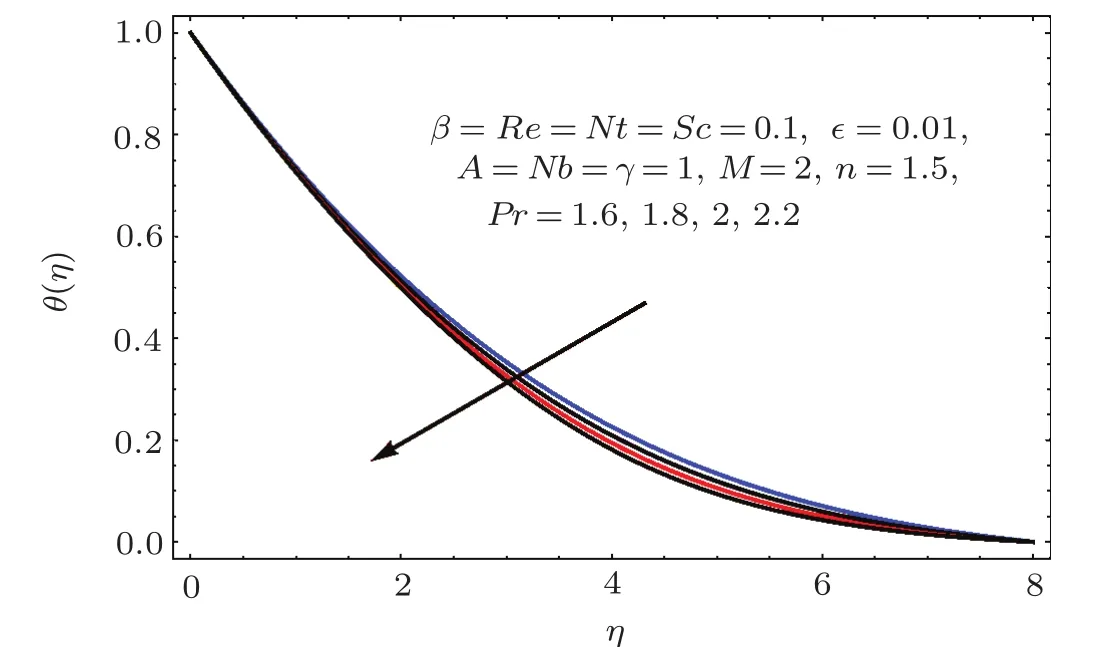
Fig.1 7 Behavior of Pr on θ(η).

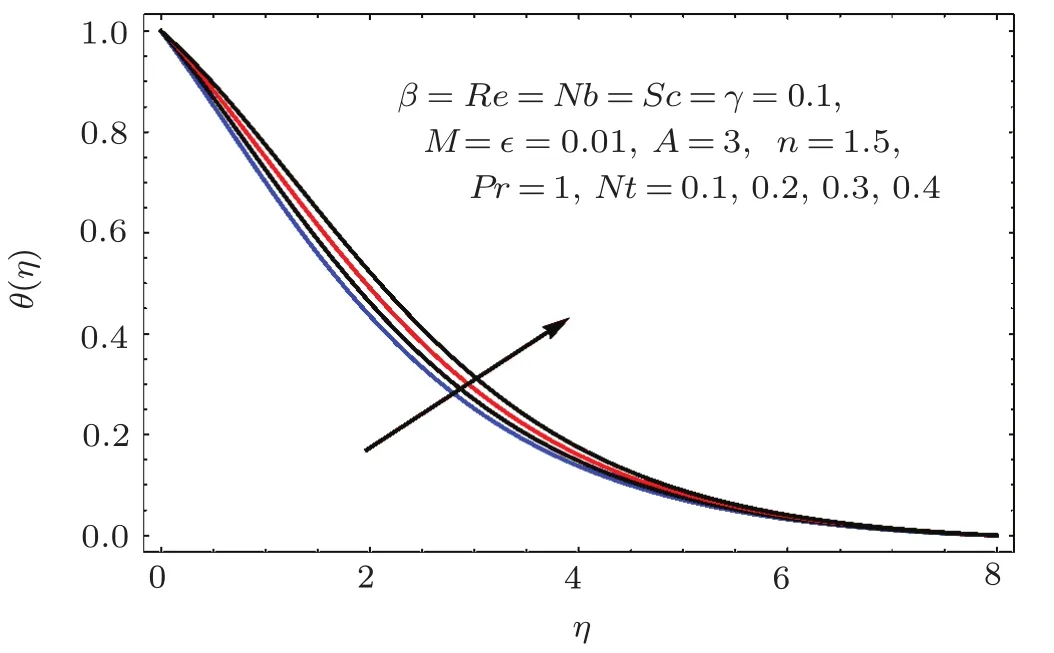
Fig.1 8 Effect of Nt on θ(η).

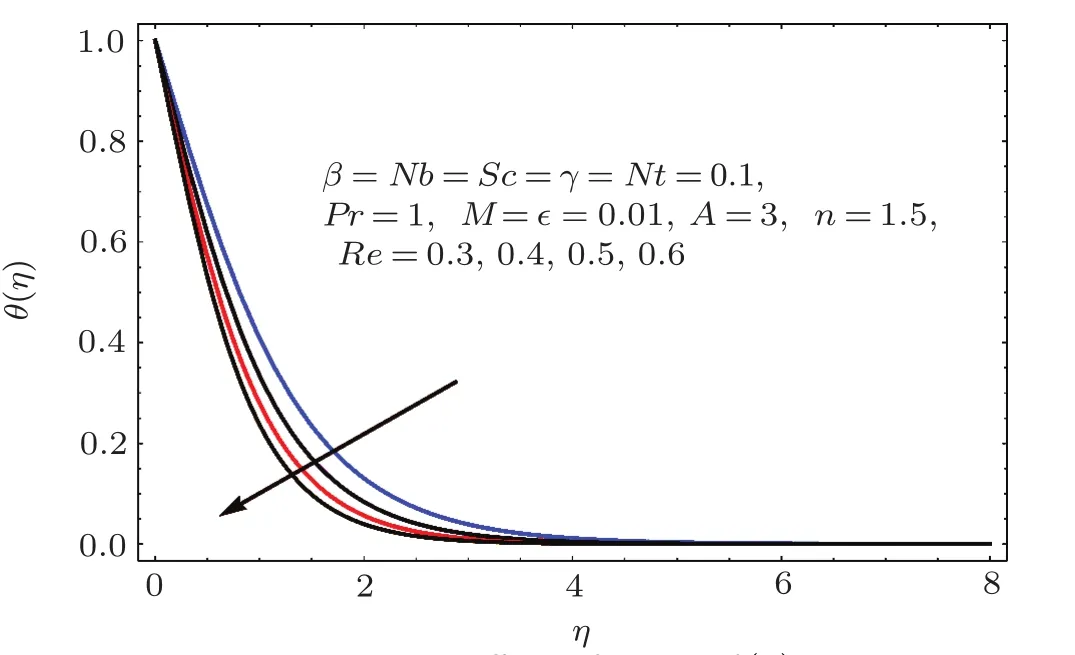
Fig.1 9 Effect of Re on θ(η).

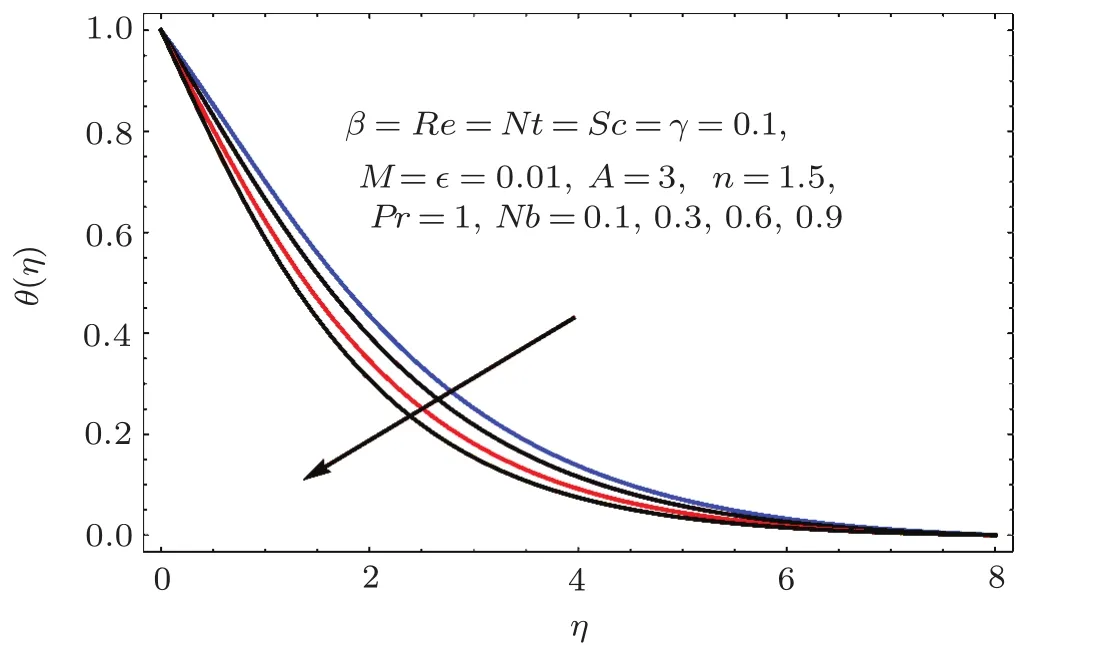
Fig.2 0 Effect of Nb on θ(η).

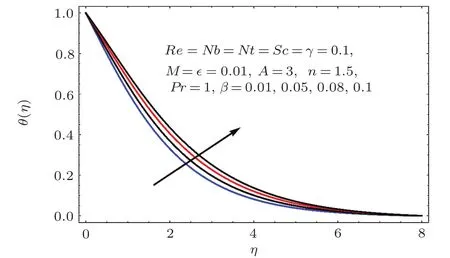
Fig.2 1 Effect of β on θ(η).

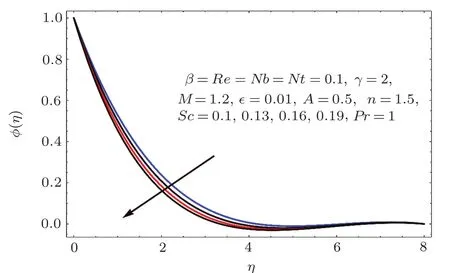
Fig.2 2 Effect of Sc on ϕ(η).

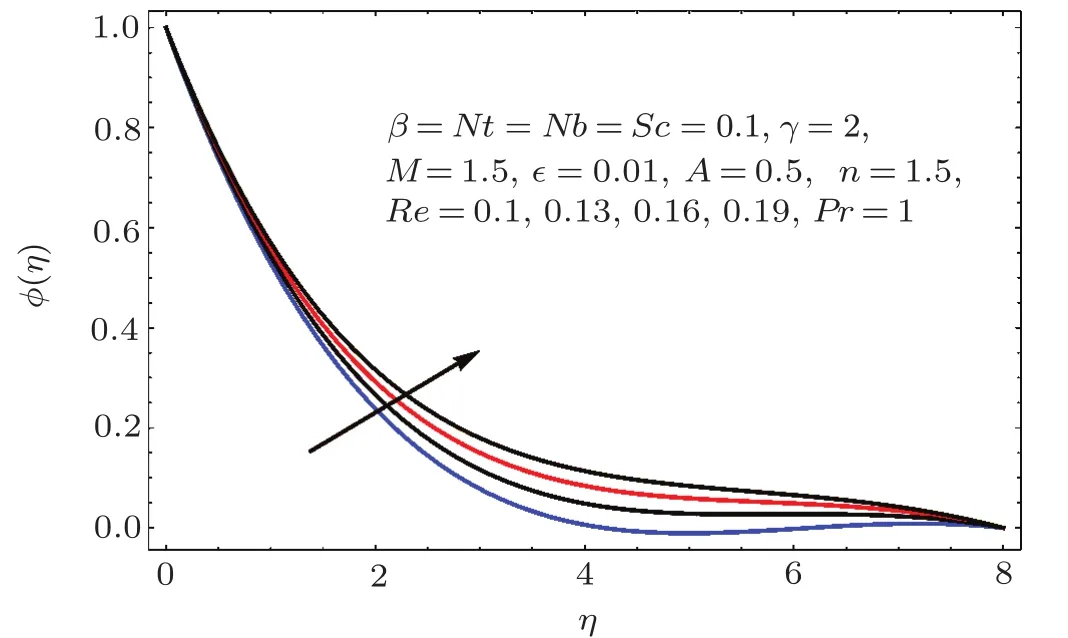
Fig.2 3 Effect of Re on ϕ(η).

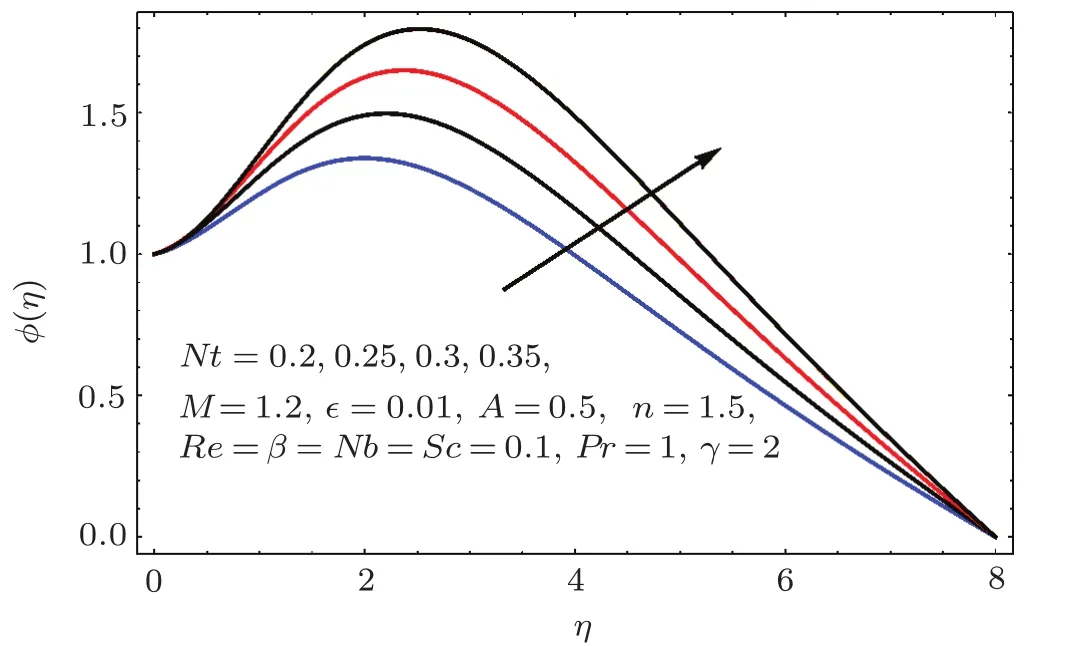
Fig.2 4 Behavior of Nt on ϕ(η).

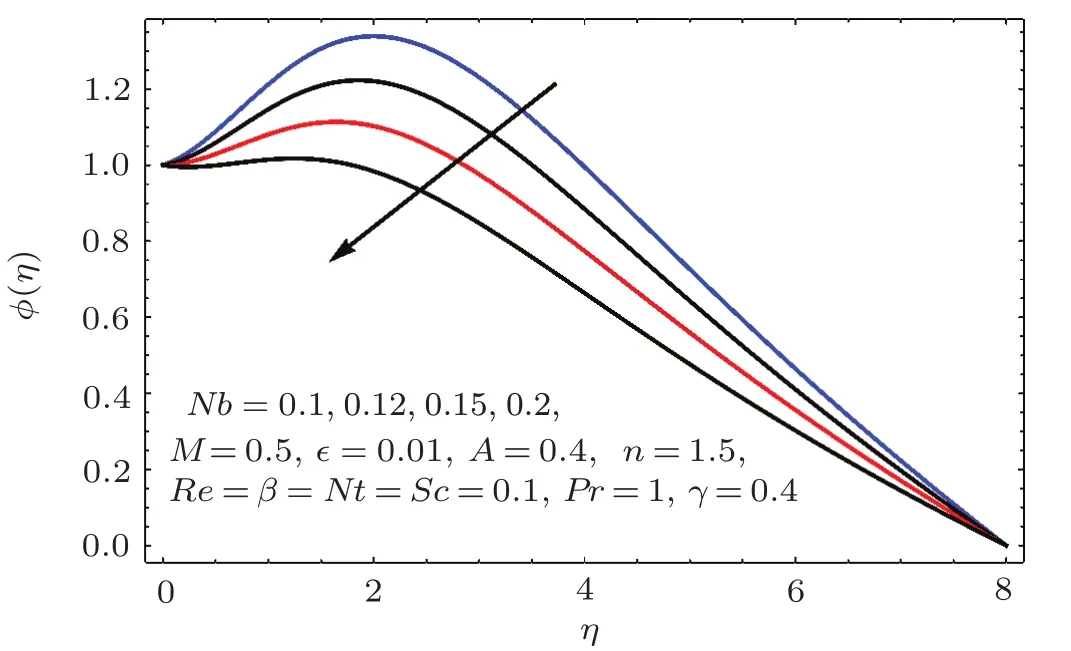
Fig.2 5 Effect of Nb on ϕ(η).

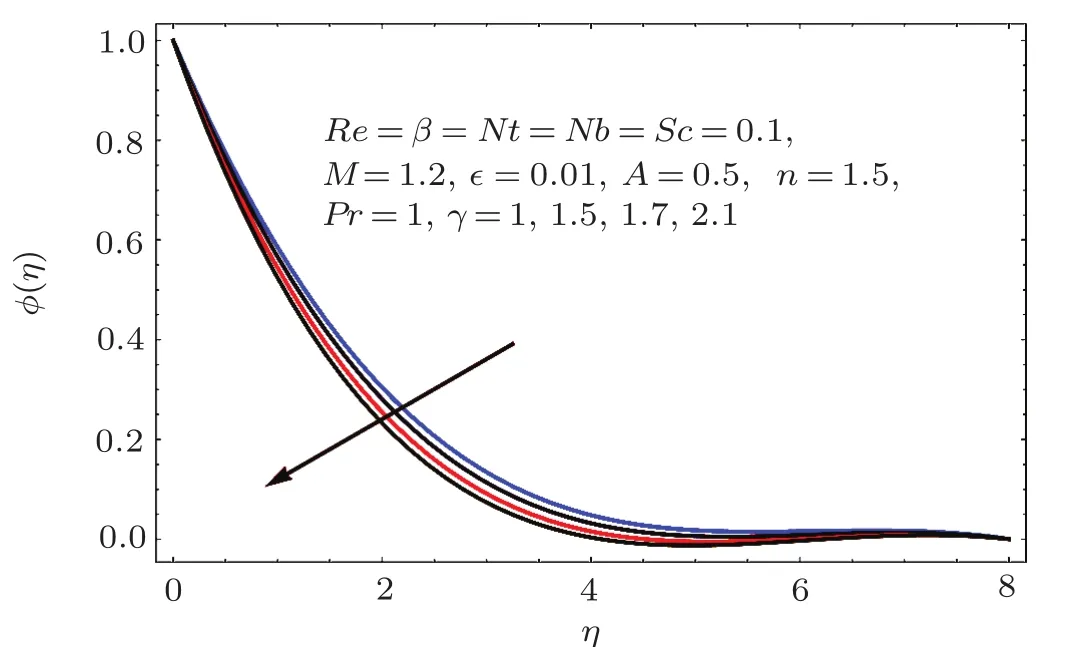
Fig.2 6 Effect of γ on ϕ(η).

Figure 22 indicates that concentration(ϕ(η))reduces for higher estimation of Schmidt number(Sc).As Sc is the ratio of viscosity to mass diffusivity.Thus for larger Sc the mass diffusivity is smaller than viscosity so the concentration field decays.On the other hand for larger values of Reynolds number the concentration field enhanced(see Fig.23).Physically for larger values of Reynolds number the viscous forces decrease and therefore concentration is enhanced.

Figure 24 sketched the impact of thermophoresis variable(Nt)on concentration(ϕ(η)).As expected is an ϕ(η)increasing function of Nt.Physically thermophoresis force transmits nanoparticles from warm to cold region.That is why associated thickness of boundary layer is enhanced.Characteristic of Brownian parameter(Nb)on concentration distribution ϕ(η)is evaluated in Fig.25.Dominant behavior of concentration is observed for smaller values of Brownian motion parameter.It is interpreted that for higher Brownian motion parameter(Nb),the collision of fluid particles enhances and concentration decreases.Figure 26 illustrates the influence of chemical reaction variable(γ)on concentration(ϕ(η)).It is noticed that concentration(ϕ(η))reduces with an increase in chemical reaction variable(γ).Physically higher variation of γ correspond to larger rate of destructive chemical reaction which terminates or dissolves the liquid specie more effectively.Therefore concentration pro fi le decays.

4 Conclusion

Flow of Sutterby nano fluid due to rotating stretchable disk has been investigated.Major points are listed below:

• Radial velocity(f′(η))is enhanced with A while reduces with Re,n,M,and ϵ.

• Axial velocity(f(η))boosts via A however it decays through Re,n,M,and ϵ.

•Elevation in Pr,Re and Nb corresponds to smaller temperature profile however temperature enhances with Nt and β.

•Concentration pro file decays for Nb,Sc and γ and it boosts via Re and Nt.

•Temperature gradient enhances for larger estimations of Pr,Re,and Nb.

•Velocity gradient is higher for Re and M.Velocity gradient decays through n,ϵ and A.

• Sherwood number boosts via Nb,Sc,γ,Nt,Re,and β.

[1]S.U.S.Choi,ASME FED 66(1995)99.

[2]J.Buongiorno,ASME J.Heat Transf.128(2006)240.

[3]Y.Lin,L.Zheng,X.Zhang,et al.,Int.J.Heat Mass Transf.84(2015)903.

[4]F.M.Abbasi,S.A.Shehzad,T.Hayat,and B.Ahmad,J.Magn.Magn.Mater.404(2016)159.

[5]T.Hayat,S.Qayyum,M.Imtiaz,and A.Alsaedi,Int.J.Heat Mass Transf.102(2016)723.

[6]A.Malvandi,A.Ghasemi,and D.D.Ganji,Int.J.Thermal Sci.109(2016)10.

[7]R.Ellahi,M.Hassan,and A.Zeeshan,Int.J.Heat Mass Transf.81(2015)449.

[8]M.Sheikholeslami,M.G.Bandpy,R.Ellahi,and A.Zeeshan,J.Magn.Magn.Mater.369(2014)69.

[9]M.Farooq,M.I.Khan,M.Waqas,et al.,J.Mol.Liq.221(2016)1097.

[10]T.Hayat,M.Sha fi que,A.Tanveer,and A.Alsaedi,J.Magn.Magn.Mater.407(2016)51.

[11]A.Postelnicu,Heat Mass Transf.43(2007)595602.

[12]B.R.Rout,S.K.Parida,and S.Panda,Int.J.Chem.Eng.2013(2013)296834.

[13]S.A.Shehzad,T.Hayat,M.Qasim,and S.Asghar,Braz.J.Chem.Eng.30(2013)187.

[14]J.V.R.Reddy,V.Sugunamma,N.Sandeep,and C.Sulochana,J.Nigerian Math.Soci.35(2016)48.

[15]T.Hayat,M.Rashid,M.Imtiaz,and A.Alsaedi,AIP Advances 5(2015)067169.

[16]T.Hayat,M.I.Khan,M.Waqas,et al.,Chin.J.Chem.Eng.25(2016)257.

[17]M.M.Rashidi,S.Bagheri,E.Momoniat,and N.Freidoonimehr,Ain Shams Eng.J.8(2017)77.

[18]M.Khan,W.A.Khan,and A.S.Alshomrani,Int.J.Heat Mass Transf.101(2016)570.

[19]A.K.A.Hakeem,S.Saranya,and B.Ganga,J.Mol.Liq.230(2017)445.

[20]T.Hayat,S.Ahmad,M.I.Khan,and A.Alseadi,Results Phys.7(2017)3419.

[21]T.Hayat,M.I.Khan,M.Farooq,T.Yasmeen,and A.Alsaedi,J.Mol.Liq.220(2016)49.

[22]T.Hayat,M.Tamoor,M.I.Khan,and A.Alsaedi,Results Phys.6(2016)1031.

[23]T.Hayat,M.I.Khan,S.Qayyum,and A.Alsaedi,Chin.J.Phys.55(2017)2501.

[24]T.Hayat,M.I.Khan,M.Tamoor,et al.,Res.Phys.7(2017)1824.

[25]M.I.Khan,M.Waqas,T.Hayat,and A.Alsaedi,J.Colloid Interface Science 498(2017)85.