基于压痕响应各向异性板料的硬化指数

惠 钰，吴建军，王明智，展学鹏，樊 赫



基于压痕响应各向异性板料的硬化指数

惠 钰，吴建军，王明智，展学鹏，樊 赫

(西北工业大学 机电学院，西安 710072)

正确识别各向异性材料力学性能中的应变硬化指数是金属成形模拟分析的重要部分。针对各向异性材料，讨论了单一方向的应变硬化指数对复杂应力问题求解的局限性，提出了一种基于扩展孔洞模型计算等效应变硬化指数的新方法。基于该方法，以TC1M钛合金板为研究对象，结合数值分析推导出载荷−接触半径曲线斜率变化比与等效应变硬化指数的关系式。通过对比和分析单一硬化指数和等效硬化指数对有限元模拟结果中材料应力应变关系的影响，验证了球形压痕法所得等效应变硬化指数对复杂应力问题的适用性。

各向异性板料；应变硬化指数；球形压痕；复杂应力

随着现代航空制造业的发展，各向异性板料(如钛合金板料)在飞机生产中的应用日益广泛[1−2]。传统加工过程的工艺分析方法已经不能满足航空发展的需要。计算机技术的飞速发展，使得数值模拟技术在金属板料成形中得到广泛应用[3−8]。

在经典塑性理论中常用到MISES[9]屈服准则和TRESCA[10]屈服准则，这两个屈服准则只适用于各向同性材料[11]。对于各向异性塑性行为的描述，学者们提出了多种各向异性屈服准则。1948年，HILL[12]首次将各向异性系数引入屈服准则，提出了Hill48屈服准则。由于该准则具有良好的理论基础，且计算简单，从而被广泛用于板料平面各向异性的描述和板料成形的有限元数值模拟[13]。在此之后，HILL[14−16]又分别提出了Hill79、Hill90和Hill93等一系列屈服准则。BARLAT等[17−21]先后又提出了多个各向异性屈服准则，如Barlat(YLD89)，Barlat(YLD91)，Barlat(YLD96)，Barlat(YLD2000-2d)和Barlat(YLD2004-18p)。与Hill48屈服准则相比，这些屈服准则参数求解复杂，尚未得到广泛的应用[22]。

在Hill48准则进行有限元模拟时，需要根据材料性能的实验数据来确定材料塑性参数。目前，普遍采用的是选取材料任意一个方向作为参考方向，输入该方向的应力应变曲线，计算相应的各向异性参数，再进行有限元计算[23−24]。然而，选取的参考方向不同，所得到的计算结果也不相同。针对复杂应力问题应当选取哪个方向为参考方向，目前相关研究较少。

在各向异性板料成形有限元模拟过程中，对于分析单向应力状态问题，通过输入该方向所得应力应变曲线可获得较准确的仿真结果。而在分析复杂应力问题，因为选择参考方向的随意性，可能造成计算结果的较大偏差。因此，在分析复杂应力问题时，需要寻求一种合适的解决方法，以减少参考方向选择随意性所引起的计算偏差。

本文作者基于扩展孔洞模型,结合ABAQUS有限元数值模拟，建立一种通过载荷−接触半径曲线斜率变化确定等效应变硬化指数的方法，为各向异性板料成形问题的准确有限元模拟提供一种较好的解决办法。

1 基于孔洞模型理论的等效应变硬化指数计算

1970年，JOHNSON[25]提出了一种经典的扩展孔洞模型(ECM)，推导出压痕底部应力应变分布变形规律，将压痕底部变形区分为3个部分：1) 接触半径为的半圆形区域为静水压力i的作用区域；2) 从接触半径到半径为的弧形带区域为塑性区域；3) 接触半径大于的区域为弹性区域。压头与试件接触表面的平均压力为m，为到压痕中心的距离，=时所在的圆弧为静水压力区与塑性区的边界，=时所在的圆弧为塑性区与弹性区的边界[26]。1985年，JOHNSON[26]将压头与试件接触表面的平均压力m与静水压力i之间的关系表示为

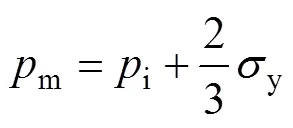
图1所示为基于扩展孔洞模型下应力区域分布图。其中，与表示材料平面方向，为加载载荷方向。

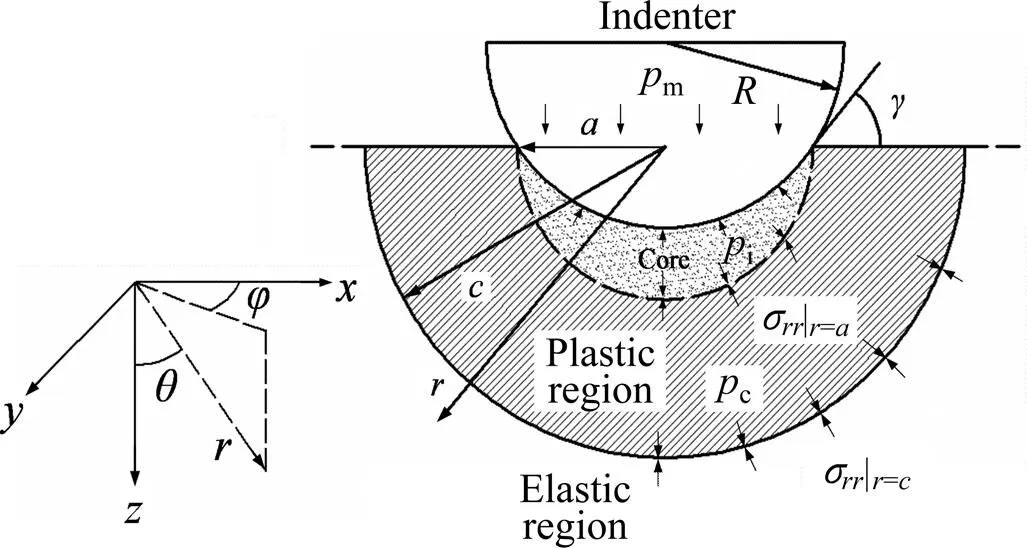
图1 扩展孔洞模型示意图

然而，这种经典的孔洞模型虽然简单，但未考虑到材料的硬化效应，仅适用于分析理想塑性材料。2006年，GAO[27]基于传统扩展孔洞对服从Holloman硬化的材料进行研究。对于服从Holloman硬化的材料，应力应变关系如下：

(3)

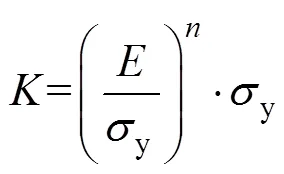
GAO[27]推导出孔洞模型中径向应变和径向应力：

2013年，KANG等[28]在JOHNSON[26]研究基础上，考虑静水区在压痕加载过程中的强化效应，引入了比例因子，从而提出了一种能够描述应变硬化的扩展孔洞模型。对于服从硬化准则的材料的静水压力i与平均接触应力m关系表示为

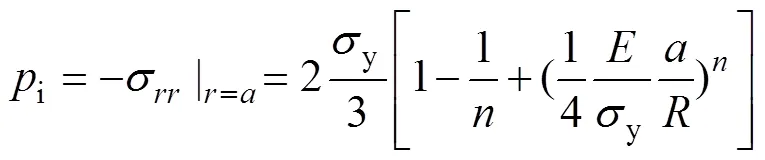
由平均接触应力的定义可得到

式中：为压痕实验时施加在刚性压头上的载荷；为压痕实验时压头与试件的接触面积，可以用接触半径表示为

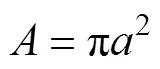
由式(3)、(10)、(11)和(12)可得

则

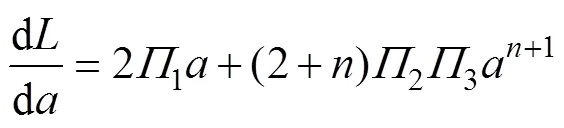
其中

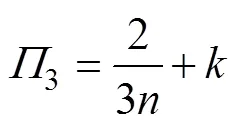
由于应变硬化指数的本质拉伸曲线硬化斜率的增量，因此它与压痕载荷曲线的斜率变化密切相关。选取载荷曲线上两个接触半径1和2，将该接触半径所对应的载荷−接触半径曲线的斜率之比s表示为

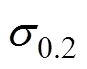
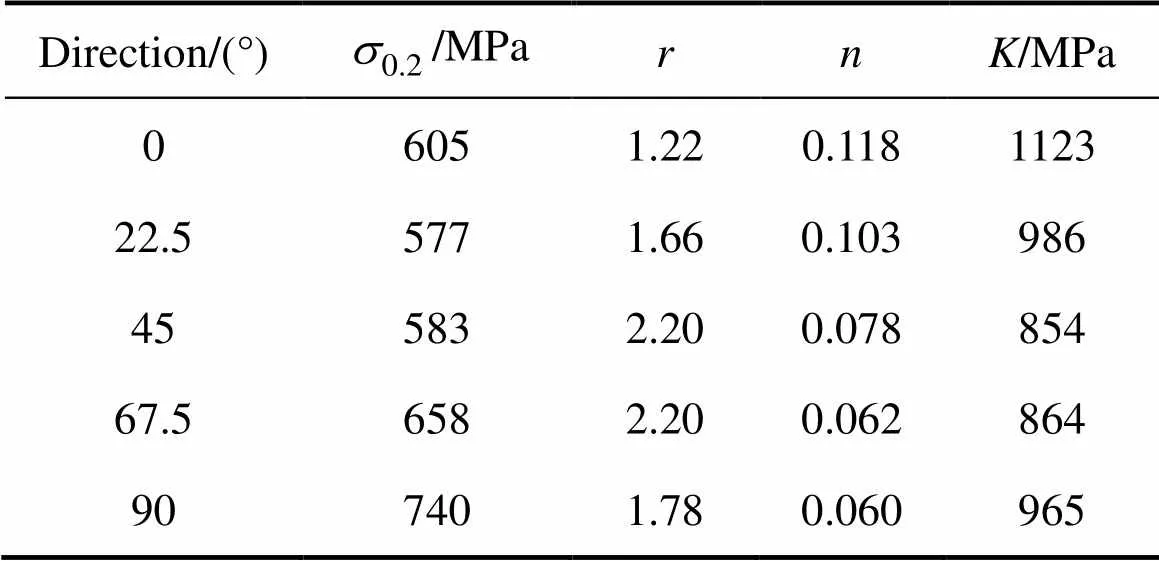
表1 TC1M材料板料的单向拉伸性能[29]

由表1可以看出，TC1M板料的各方向屈服应力范围在500~800 MPa之间。当=100 GPa时，应变范围为0.005~0.008。取压头半径=250 μm，两个接触半径：1=150 μm，2=200 μm。根据式(13)、(14)和(16)可得，当弹性模量和压头半径一定时，选取固定的接触半径1和2，则斜率比s与应变和应变硬化指数关系如图2所示。

图2 应变硬化指数与加载斜率的关系曲线

由图2可以看出，不同应变对斜率比s的影响几乎可以忽略。在此不考虑不同应变对应变硬化指数的影响，该斜率比与材料的硬化特性主要相关。对图2中数据曲线用一元三次多项式进行拟合，得到

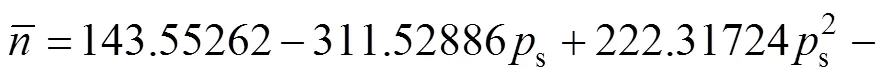
由于大多数弹塑性金属材料的应变硬化指数取值范围在(0, 0.5)区间内，所以对于式(17)，仅考虑斜率比s取值范围为(1.41138, 1.54074)。

为了简化各向异性材料分析模型，将面内异性材料压痕底部的区域平均地分为3部分，分别按照0°(轧制方向)、45°(对角方向)、90°(横纹方向)所对应的力学参数计算，示意图如图3所示。

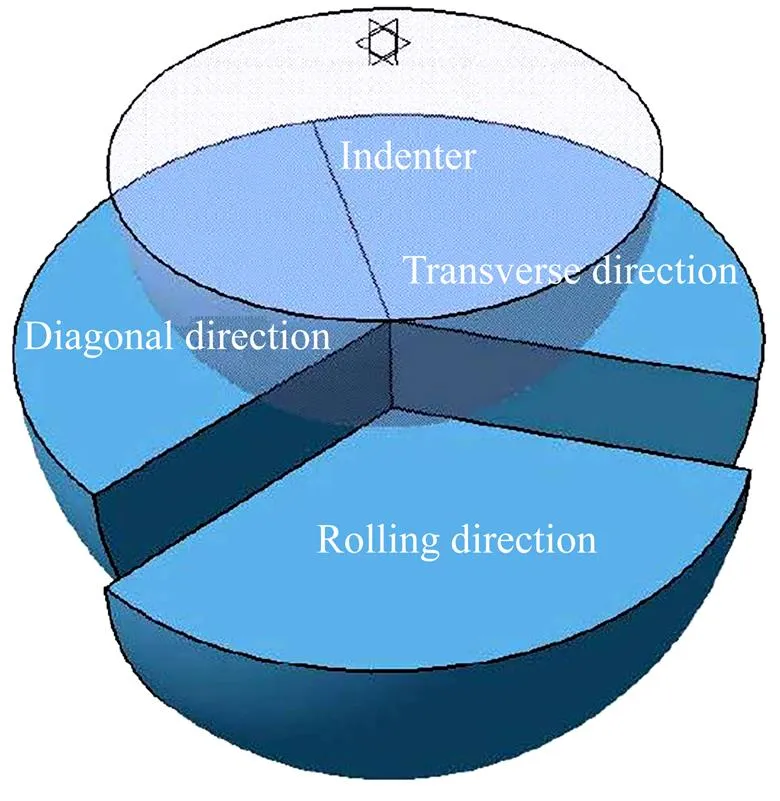
图3 压痕底部分块示意图

根据简化模型，式(12)可改写为

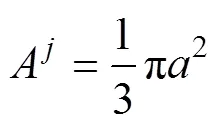
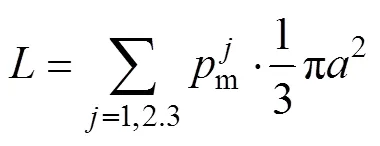
其中=1, 2, 3分别表示轧制方向、对角方向以及横纹方向的材料参数。

根据式(18)，TC1M板料压头载荷和接触半径关系如图4所示。根据图4获取接触半径2=200 μm和1=150 μm时曲线的斜率，根据式(16)计算斜率比s。

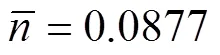
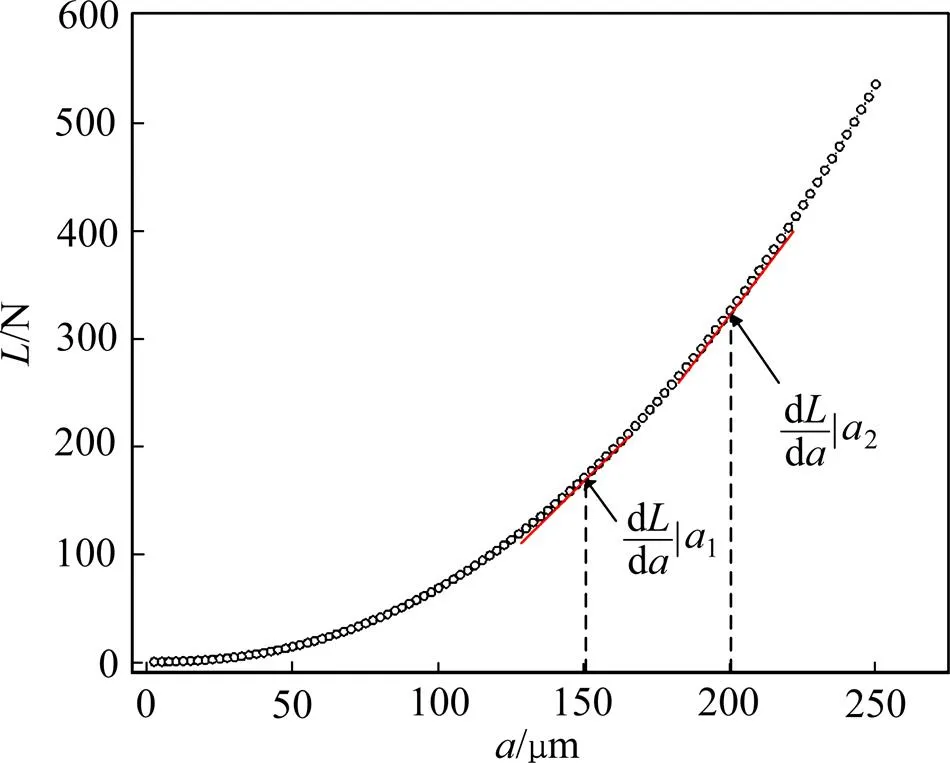
图4 压头载荷与接触半径的关系

2 应变硬化指数的应用

采用通用商业有限元软件ABAQUS进行有限元仿真实验，其中ABAQUS®商用有限元软件，由于其强大的非线性力学分析能力，已经越来越多地得到工程应用。而在现有的ABAQUS®软件中，针对各向异性材料的屈服准则，主要有Hill48[12]屈服准则。有限元模型建立如图5所示。

图5 压痕仿真实验中使用的有限元模型示意图

采用Hill48各向异性来描述材料的各向异性，其中11、22、33、13、12、23为材料6个方向上的比值。定义11方向为(轧制方向)，22方向为(横纹方向)，33方向为(厚度方向)，定义压头与试件的接触摩擦因数为=0.15，压痕深度为t=0.01 mm。

在ABAQUS中，材料属性设置输入应力应变点对时，选取轧制方向为参考方向，硬化指数选择有以下两种方式。

1) 单向硬化指数计算

对于各向异性材料有限元模拟，通过单向拉伸试验得到轧制方向上的应变硬化指数，进而得到应力应变曲线，输入该曲线进行计算。

2) 等效硬化指数计算

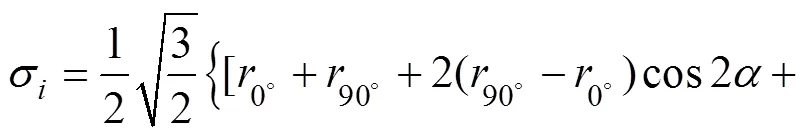
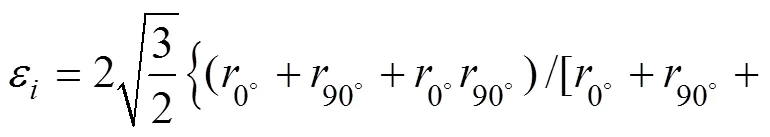
由式(3)、(19)、(20)可得：

3 两种应变硬化指数对有限元计算结果影响及其讨论

图6所示为摩擦因数=0.15、压入深度为t/=5%时不同取点深度的等效塑性应变分布。由图6可以看出，随着取点深度的增大，应变分布趋于平缓，各向异性特性逐渐减弱。若取点在压头与试件接触表面时，即/=0%时，板料各向异性特性明显，但等效塑性应变会出现震荡；若在距离试件表面为/=1%时，等效塑性应变分布平缓，且可以表现出各向异性；随着取点深度的增加，当/=2%时，等效塑性应变更为平缓，但缺点是不再表现各向异性特性。这是由于各向异性主要存在于试件表层，随着取点深度的增加，压痕底部不同方向上应力应变分布的差异性逐渐减小。在深度为/=1%时，考虑摩擦因数对等效塑性应变的影响，当摩擦因数分别等于0.10、0.15、0.20时，等效塑性应变分布如图7所示。

由图7可以看出，从压头中心到压头与试件相接触位置底部区域，摩擦因数对于应变分布的影响较大，而在压头与试件接触边缘沿着远离压入中心方向，摩擦因数的影响逐渐减小，可以看出2/≥0.025时，摩擦因数对输出点的影响较小。

所以结合应变分布梯度以及摩擦因数对等效塑性应变的影响，以下讨论的输出点均位于/=1%、2/=0.025处。

计算完成之后分别提取在0°、22.5°、45°、67.5°、90°方向上的应力−应变曲线，结果如图8所示。

图6 距离试件表面不同深度下等效塑性应变分布

图7 不同摩擦因数作用下等效塑性应变分布

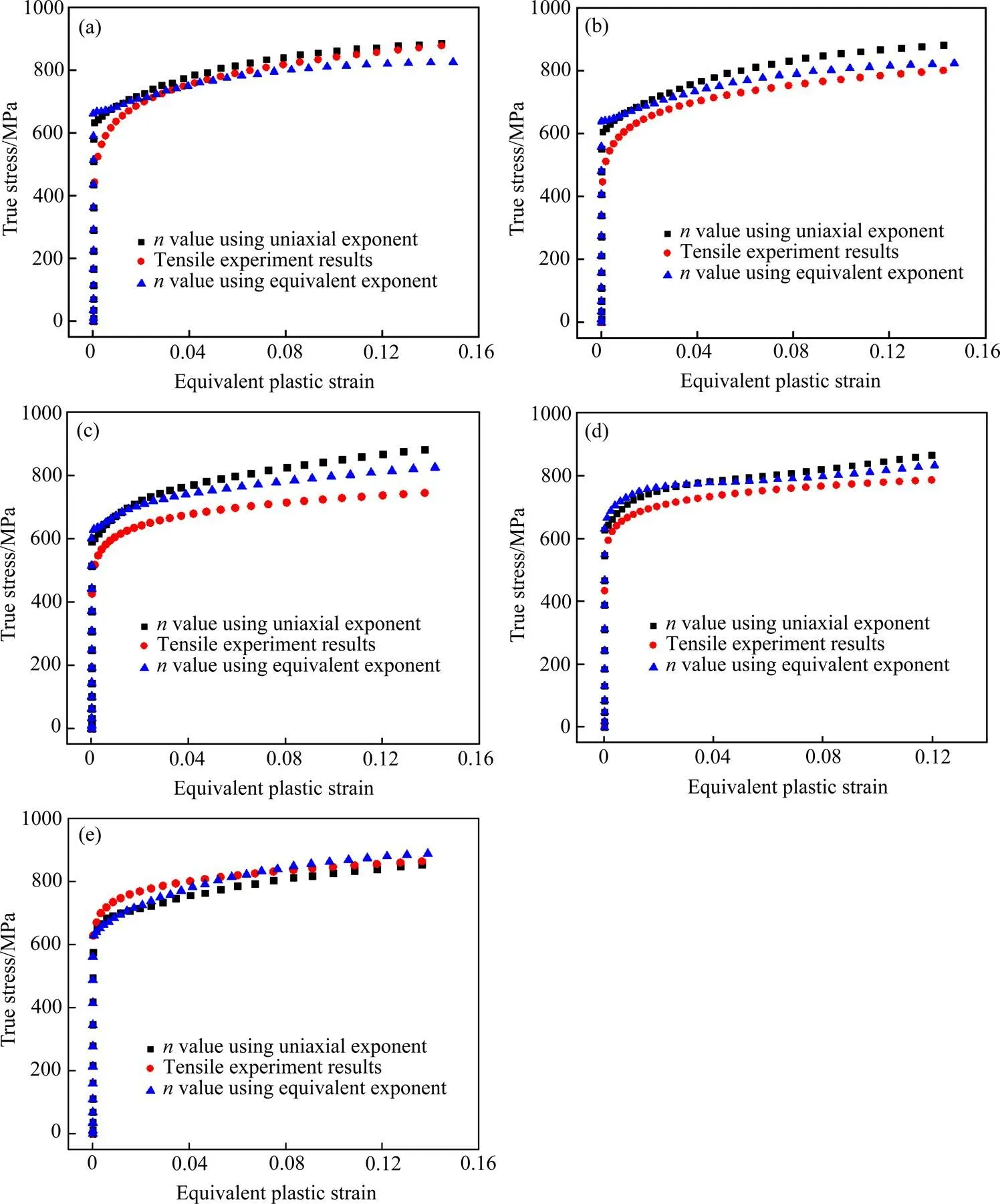
图8 不同方向上不同n值的对比结果

4 结论

2) 深入讨论了应变梯度分布及摩擦因数对表征结果的影响，提出了针对各向异性材料表征应力应变最优获取位置。

3) 通过数值及实验研究，验证了所提出等效应变硬化指数计算方法的有效性，及其对于复杂应力状态问题的适用性。

[1] WEAVER J S, KALIDINDI S R. Mechanical characterization of Ti-6Al-4V titanium alloy at multiple length scales using spherical indentation stress-strain measurements[J]. Materials & Design, 2016, 111: 463−472.

[2] KIM K H, KIM Y C, JEON E C, KWON D. Evaluation of indentation tensile properties of Ti alloys by considering plastic constrain effect[J]. Materials Science and Engineering A, 2011, 52: 5259−5263.

[3] 张飞飞, 陈劼实, 陈 军, 黄晓忠, 卢 健. 各向异性屈服准则的发展及实验验证综述[J]. 力学进展, 2012, 42(1): 68−80.ZHANG Fei-fei, CHEN Jie-shi, CHEN Jun, HUANG Xiao-hzong, LU Jian. Review on development and experimental validation for anisotropic yield criterions[J]. Advances in Mechanics, 2012, 42(1): 68−80.

[4] XIAO S L, JING T, XU L J, CHEN Y Y, YU H B, HAN J C. Microstructures and mechanical properties of TiAl alloy prepared by spark plasma sintering[J]. Transactions of Nonferrous Metals Society of China, 2009, 19(6): 1423−1427.

[5] PATEL D K, KALIDINDI S R. Correlation of spherical nanoindentation stress−strain curves to simple compression stress−strain curves for elastic-plastic isotropic materials using finite element models[J]. Acta Materialia, 2016, 112: 295−302.

[6] 倪向贵, 吴恒安, 王 宇, 王秀喜. 各向异性本构关系在板料成形数值模拟中的应用[J]. 计算力学学报, 2003, 20(2): 231−235.NI Xiang-gui, WU Heng-an, WANG Yu, WANG Xiu-xi. Application of anisotropic constitutive equations to numerical simulation of sheet forming[J]. Chinese Journal of Computational Mechanics, 2003, 20(2): 231−235.

[7] CAO Q, ZHANG Q, ZHANG X. Anisotropy of mechanical behavior in commercially pure titanium sheets[J]. Journal of Harbin Institute of Technology, 2015, 22(1): 63−67.

[8] WANG M, WU J, HUI Y, ZHANG Z, ZHAN X, GUO R. Identification of elastic-plastic properties of metal materials by using the residual imprint of spherical indentation[J]. Materials Science & Engineering A, 2017, 679: 143−154.

[9] CAPSONI A, CORRADI L. Variational formulations for the plane strain elastic-plastic problem for materials governed by the von Mises criterion[J]. International Journal of Plasticity, 1996, 12(4): 547−560.

[10] TRESCA H. Memoir on the flow of solid bodies under strong pressure[J]. Comptes Rendus Acad Sci, 1986, 59: 754−760.

[11] 严 勇, 吴 超, 胡志力, 黄 松, 华 林. 汽车铝合金覆盖件成形数值模拟的各向异性屈服准则研究[J]. 塑性工程学报, 2016(2): 92−97.YAN Yong, WU Chao, HU Zhi-li, HUANG Song, HUA lin. Anisotropic yield criterion for automotive aluminum panels forming numerical simulation[J]. Journal of Plasticity Engineering, 2016, 23(2): 92−97.

[12] HILL R. A Theory of the yielding and plastic flow of anisotropic metals[J]. Proceedings of the Royal Society of London, 1948, 193(1033): 281−297.

[13] WANG M, WU J, ZHAN X, GUO R, HUI Y, FAN H. On the determination of the anisotropic plasticity of metal materials by using instrumented indentation[J]. Materials & Design, 2016, 111: 98−107.

[14] CHU E. Generalization of Hill’s 1979 anisotropic yield criteria[J]. Journal of Materials Processing Technology, 1995, 50(1): 207−215.

[15] HILL R. Constitutive modelling of orthotropic plasticity in sheet metals[J]. Journal of the Mechanics & Physics of Solids, 1990, 38(3): 405−417.

[16] HILL R. A user-friendly theory of orthotropic plasticity in sheet metals[J]. International Journal of Mechanical Sciences, 1993, 35(1): 19−25.

[17] BARLAT F. Plastic behavior and stretch ability of sheet metals. Part I: A yield function for orthotropic sheets under plane stress conditions[J]. International Journal of Plasticity, 1989, 5(1): 51−66.

[18] BARLAT F, LEGE D J, BREM J C. A six-component yield function for anisotropic materials[J]. International Journal of Plasticity, 1991, 7(7): 693−712.

[19] BARLAT F, MAEDA Y, CHUNG K, YANAGAWA M,BREM J C, HAYASHIDA Y, LEGE D J, MATSUI K, MURTHA S J, HATTORI S, MAKOSEY S. Yield function development for aluminum alloy sheets[J]. Journal of the Mechanics & Physics of Solids, 1997, 45(11/12): 1727−1763.

[20] BARLAT F, BREM J C, YOON J W, CHUNG K, DICK R E, LEGE D J, POURBOGHRAT F, CHOI, S H, CHU E. Plane stress yield function for aluminum alloy sheets—Part 1: Theory[J]. International Journal of Plasticity, 2003, 19(9): 1297−1319.

[21] BARLAT F, ARETZ H, YOON J W, KARABIN M E, BREM J C, DICK R E. Linear transformation-based anisotropic yield functions[J]. International Journal of Plasticity, 2005, 21(5): 1009−1039.

[22] 王海波, 万 敏, 阎 昱, 吴向东. 参数求解方法对屈服准则的各向异性行为描述能力的影响[J]. 机械工程学报, 2013, 49(24): 45−53.WANG Hai-bo, WAN Min, YAN Yu, WU Xiang-dong. Effect of solving method of parameters on the description ability of the yield criterion about the anisotropic behavior[J]. Journal of Mechanical Engineering, 2013, 49(24): 45−53.

[23] KALKHORAN S M, CHOI W B, GOULDSTONE A. Estimation of plastic anisotropy in Ni-5%Al coatings via spherical indentation[J]. Acta Materialia, 2012, 60(3): 803−810.

[24] YONEZU A, TANAKA M, KUSANO R, CHEN X. Probing out-of-plane anisotropic plasticity using spherical indentation: A numerical approach[J]. Computational Materials Science, 2013, 79: 336−344.

[25] JOHNSON K L. The correlation of indentation experiments[J]. Journal of the Mechanics & Physics of Solids, 1970, 18(2): 115−126.

[26] JOHNSON K L. Contact mechanics[J]. Journal of Tribology, 1985, 108(4): 464.

[27] GAO X L. An expanding cavity model incorporating strain-hardening and indentation size effects[J]. International Journal of Solids & Structures, 2006, 43(21): 6615−6629.

[28] KANG S K, KIM Y C, KIM K H, KIM J Y, KWON D. Extended expanding cavity model for measurement of flow properties using instrumented spherical indentation[J]. International Journal of Plasticity, 2013, 49(10): 1−15.

[29] 吴建军, 周维贤. 板料成形性基本理论[M]. 西安: 西北工业大学出版社, 2010.WU Jian-jun, ZHOU Wei-xian. Basic theory of sheet forming[M]. Xi’an: Northwestern Polytechnical University Press. 2010: 55−59.

[30] TABOR D. A simple theory of static and dynamic hardness[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1948, 192(1029): 247−274.

[31] LEE H, JIN H L, PHARR G M. A numerical approach to spherical indentation techniques for material property evaluation[J]. Journal of the Mechanics & Physics of Solids, 2005, 53(53): 2037−2069.

Strain-hardening exponent of anisotropic sheet based on spherical indentation response

HUI Yu, WU Jian-jun, WANG Ming-zhi, ZHAN Xue-peng, FAN He

(School of Mechanical Engineering, Northwestern Polytechnical University, Xi’ an 710072, China)

Accurate determination of the strain hardening exponent of the anisotropic materials is the fundamental part of the numerical simulation of metal forming. For anisotropic materials, the limitations were discussed when the single orientation-dependent strain hardening exponent was used in the numerical simulation of multi-stress problems. A new approach based on the expanding cavity model was proposed to identificate the strain hardening exponent of anisotropic materials. Based on this, a new relationship between the variation of the slope ratio of load−contact radius curve and the equivalent strain hardening exponent was suggested for the TC1M titanium alloys sheet, by using the numerical and theoretical analysis. The effectiveness of this method was verified by comparing the numerical results using either the single orientation-dependent strain hardening exponent or the new indentation-based strain hardening exponent. The results show that the equivalent strain hardening exponent is more suitable for the multi-stress state problem.

anisotropic sheet; strain hardening exponent; spherical indentation; multi-stress state

Project(51675431) supported by the National Natural Science Foundation of China

2017-03-03;

2017-09-26

WU Jian-jun; Tel: +86-29-88493101; E-mail: wujj@nwpu.edu.cn

1004-0609(2018)-04-0685-08

TG301

A

10.19476/j.ysxb.1004.0609.2018.04.06

国家自然科学基金资助项目(51675431)

2017-03-03；

2017-09-26

吴建军，教授，博士；电话：029-88493101；E-mail: wujj@nwpu.edu.cn

(编辑 龙怀中)