一种带有过渡因子的下压指令设计方法

罗 超，邢汇源

（1.海军航空大学，山东烟台264001；2.太原理工大学电器与动力工程学院，山西晋中030600）

近年来，由于世界各国的广泛关注，高超声速技术得到了飞速发展。以高超声速技术发展而来高超声速武器日益活跃在军备舞台上，这些发展和成就将飞行器的飞行速度由亚声速、高亚声速、超高速向高超声速推进，并使超远程精确快速打击成为可能[1-3]。高超声速飞行器因有很高的马赫数、较大的升阻比，并且再入环境十分复杂，使得设计出既有较高的计算效率，又有较高制导精度的制导律变得尤为困难[4-6]。同时，由于高超飞行器再入段弹道对控制变量十分敏感，并且再入过程又不可避免地存在各种扰动和不确定性因素，使得弹道极易偏离平稳滑翔状态，从而出现弹道震荡[7-11]。因此，为了使高超声速飞行器滑翔段能够平稳过渡至下压段，不仅需要平衡滑翔的参考弹道，还需要在再入过程中抑制扰动，以使飞行器能够按预定的航线飞行[12]。

高超声速飞行器由再入段转入下压段的过程中，由于飞行器的运动状态是渐变的，而下压指令却是预先设计好并由飞行控制系统瞬间给出的，使飞行器运动状态无法快速与制导方式匹配，留给飞行器改变运动状态的时间是很短暂的，所以在滑翔段与下压段交接的过程中，必然会出现弹道交接班的问题[13]。为了使飞行器由滑翔段转入下压段能平稳过渡，需要设计相应的下压指令。文献[14]在交接制导的过程中引入过渡段的概念，并设计了2种复合制导的过渡段交接算法—零基交接和自适应交接算法。文献[15]利用自适应交接制导算法设计了正弦函数形式的制导律。在2种交接制导算法中，零基交接算法所得的制导律需要飞行器的加速度先减小到零，然后再由零过渡到末制导加速度。零基交接算法能够实现弹道的一阶平滑过渡交接，但加速度的减小会使交接过程中瞄准误差逐渐增大，并且可能会使过渡段的需用加速度增大，过渡时间变长。自适应交接制导算法虽然改进了上述缺点，能够实现一阶平滑过渡，但无法实现弹道的二阶平滑过渡。

本文在分析高超声速飞行器平衡滑翔的参考弹道后，提出了飞行器平滑过渡的基本条件，在引入过渡因子的基础上，设计出3种带有过渡因子的下压指令，给出了不同过渡因子下的弹道仿真结果。结果表明，该算法设计思路清晰、计算量小且制导精度高。

1 平滑过渡的基本条件

高超声速飞行器从滑翔段过渡到下压段时，由于制导方式发生突变，会使原本较为平滑的弹道发生剧烈变化，这种变化对弹道的影响是不可逆的，很可能会使飞行器无法适应突然改变的运动状态而失控。[16]

1.1 下压弹道的特点

下压段是决定飞行器能否完成预定任务的关键。下压段一般是指飞行器导引头开机到命中目标或脱靶间的一段弹道，此过程中主要任务是导引头按预先设计好的位置开机，并对目标进行搜索、捕捉、选择和跟踪，并以预先设计好的导引规律将弹头导向目标[17]。在下压段，飞行器要以很高的马赫数下压俯冲，对目标实现“灌顶”攻击，因而下压弹道落点倾角一般要大于60°，飞行时间通常小于70 s，且在此过程中飞行距离一般小于100km[18]。

1.2 平滑过渡的条件

在本设计中，飞行器由滑翔段转入下压段是由航迹倾斜角γ(t)控制的，为了设计合适的再入段下压指令，下压指令的设计应该综合考虑滑翔段和下压段两个阶段的航迹倾斜角γ(t)。因此，下压指令应设计为两个阶段航迹倾斜角加权和的形式，即：

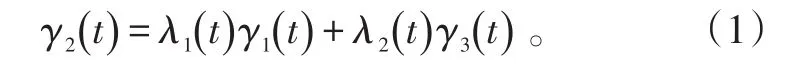
式（1）中：γ1(t)、γ3(t)分别表示滑翔段、下压段的航迹倾斜角；γ2(t)为交接过渡段的下压指令；λ1(t)、λ2(t)分别为滑翔段和下压段权重，称其为过渡因子。

实现交接过渡段平稳交接的基本条件可表示为：

1）γ2(t)与γ1(t)交接过渡段初始点平滑交接，即；

2）γ3(t)与γ2(t)在交接过渡段终点平滑交接，即：。其中：t0为交接开始时间点，Δt为交接过渡时间。

为便于计算，令交接开始时间点t0=0，则下压指令的形式为：γ2(t)=λ1(t)γ1(t)+λ2(t)γ3(t) ，t∈[0,Δt]。

那么，飞行器交接过渡段平稳交接的条件转化为：

1）γ2(t)与γ1(t)在t=0时刻满足平滑交接的条件，即；

2）γ3(t)与γ2(t)在t=Δt时刻满足平滑交接的条件，即：。

2 过渡因子的设计

高超飞行器弹道平滑交接包括2个方面：一方面是弹道的一阶平稳过渡，即γ2(t)的导数存在且连续；另一方面是飞行器弹道的二阶平稳交接，对应于的导数存在且连续。

为了设计出使弹道平稳交接的下压指令，需要先设计过渡因子λ1(t)和λ2(t)。为此对式（1）两端同时对时间t求导，可得：

根据交接过渡段平稳交接条件，有：

把式（3）代入式（1）、（2），进而求出：

由于对任何γ1(t)，γ3(t)，式（4）都要成立，因此有：

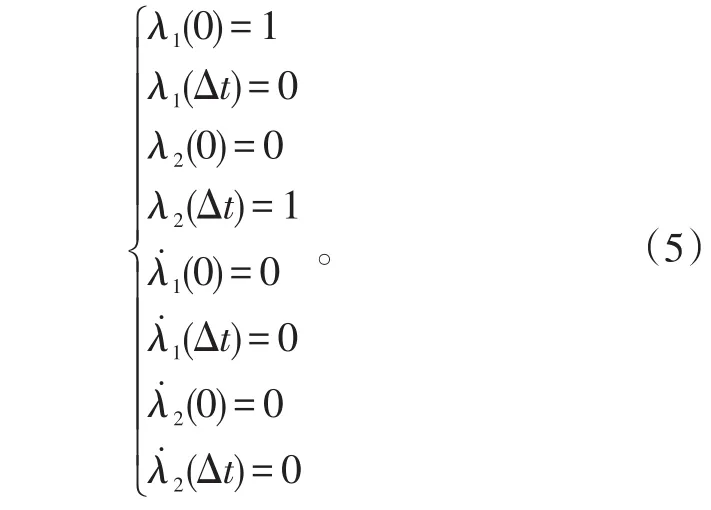
对于满足上述式（5）的过渡因子λ1(t)、λ2(t)具有很多形式，最简单也最容易想到的就是一次函数形式。

2.1 一次函数过渡因子

设一次函数过渡因子的下压指令的形式为：

式（6）两端同时对时间t求导，可得：

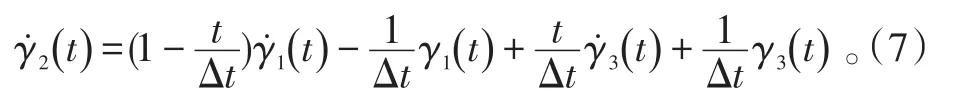
将t=0和t=Δt代入式（6），得：

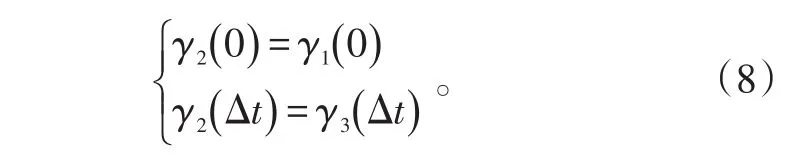
将t=0和t=Δt代入式（7），得：

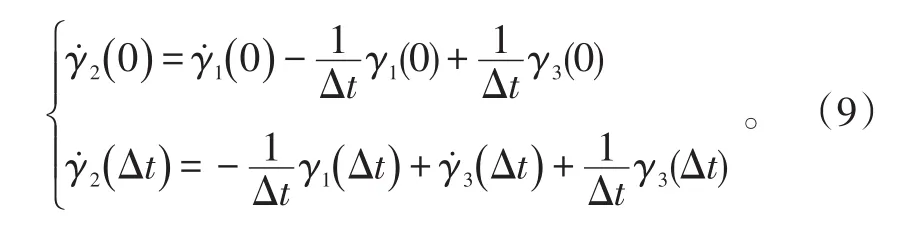
由于γ1(t)与γ3(t)分别为滑翔段和下压段的航迹倾斜角，即γ1(t)≠γ3(t)，从而有：

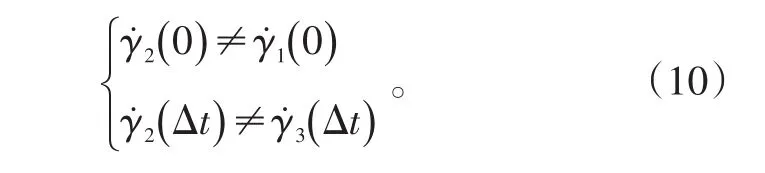
所以，一次函数形式的下压指令无法实现二阶平滑。

本文将提出一种新的过渡因子的形式，可以同时满足一阶和二阶平滑过渡。

2.2 多项式函数过渡因子

设满足式（5）的多项式过渡因子λ的形式为：

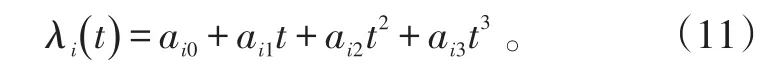
ai0、ai1、ai2、ai3分别为对应项的系数，i=1,2。

式（11）两端同时对时间t求一阶导数，有：

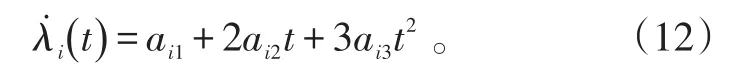
再将式（5）代入式（11）、（12），有：

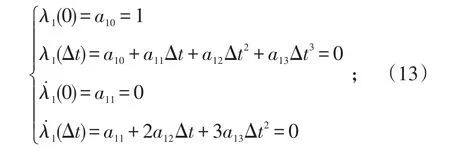
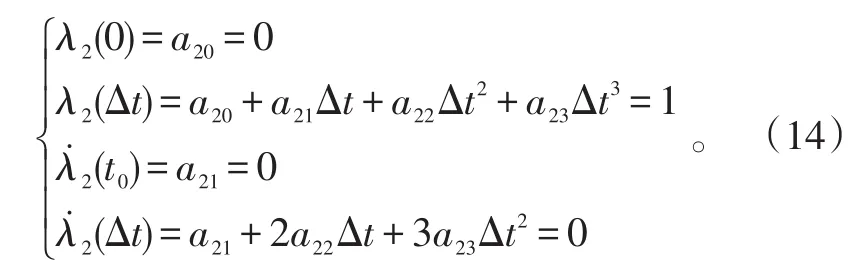
分别求解式（13）、（14），可得：

将式（15）代入式（7）中，求出多项式过渡因子：

2.3 正弦函数过渡因子

设正弦函数过渡因子的形式为：

通过2.2节中的方法可以求得：

求出正弦函数过渡因子的形式为：

2.4 指数函数过渡因子

设指数函数过渡因子的形式为：

同理可得：

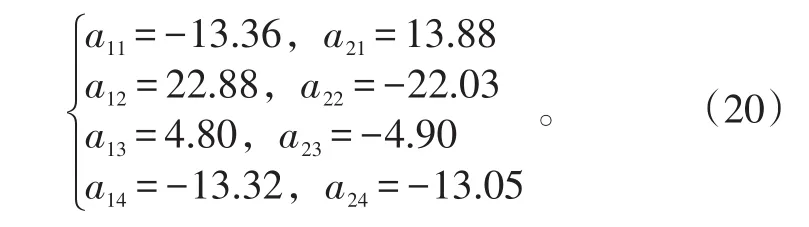
则指数函数过渡因子的形式为：

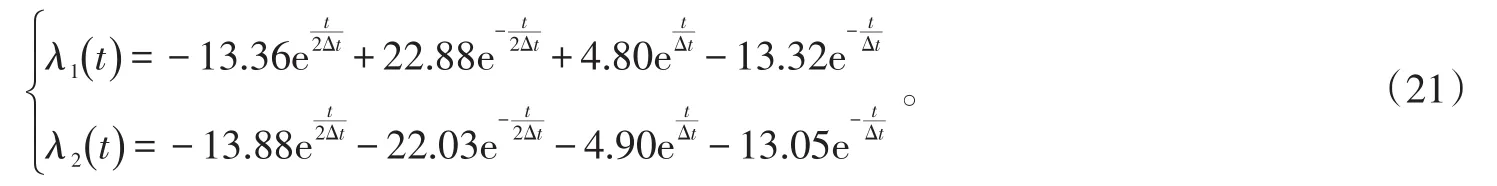
3 仿真验证

仿真的起始点设为开始滑翔的位置，飞行器先滑翔飞行，后下压飞行的方式击中目标。

在滑翔段，飞行器以正常姿态飞行约116 s，再以下压方式飞行约64 s至目标。

仿真结果如图1～5所示。

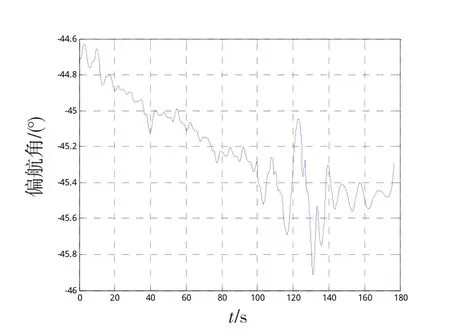
图1 直接过渡曲线Fig.1 Schematics of direct transition

图2 一次函数过渡曲线Fig.2 Schematics of linear function transition

图3 多项式函数过渡曲线Fig.3 Schematics of polynomial function transition

图5 指数函数交接曲线Fig.5 Schematics of exponential function transition

仿真结果表明，直接过渡交接时，飞行器航向变化极不稳定，特别是开始下压的时刻，航向角震荡十分剧烈，超调量陡增，最终发散，无法实现平稳过渡；一次函数下压指令过渡交接时，虽然能实现一阶平滑过渡，但无法实现二阶平滑过渡；多项式、正弦和指数下压指令过渡交接时，不仅能实现一阶平稳过渡，而且能实现二阶平稳过渡，但相对而言，指数形式的下压指令具有更加平滑的过渡效果。

4 结束语

从目前高超声速技术发展趋势来看，未来以高超声速武器为主体新型作战样式必将成为未来战争的主要模式。下压段作为高超声速武器打击目标的关键阶段，对精度的要求极为严苛，因而对于高超声飞行器由平衡滑翔段转入下压段的过程中存在的交接不平滑问题，不能只考虑滑翔段或者下压段某一阶段的弹道特性，要结合2个阶段的弹道特性进行综合分析。故本文设计的下压指令是由2个阶段航迹偏航角加权和的形式得到的。从结果来看，所设计的下压指令能够很好地解决过渡过程中存在弹道震荡问题。

[1]HUANG L，DUAN Z S，YANG J Y.Challenges of control science in near space hypersonic aircrafts[J].Control Theory&Applications，2011，28（10）：1496-1505.

[2]刘杰，何峰，吴静.未来防空反导作战中高超声速目标的发展趋势分析[J].飞航导弹，2014，（14）：19-23.LIU JIE，HE FENG，WU JING.Analysis of development trend of hypersonic speed targets in future air defense and antimissile combat[J].Winged Missiles Journal，2014，（14）：19-23.（in Chinese）

[3]王少平，董受全，李晓阳.未来高超声速反舰导弹作战使用关键问题研究[J].战术导弹技术，2016（5）：18-24.WANG SHAOPING，DONG SHOUQUAN，LI XIAOYANG.Research on key issues of operational application of hypersonic anti-ship missile[J].Tactical Missile Technology，2016（5）：18-24.（in Chinese）

[4]SERAH N D，NESRIN S K.Survey of planetary entry guidance algorithms[J].Progress in Aerospace Sciences，2014，68（1）：22-28.

[5]ZHAO J，ZHOU R.Reentry trajectory optimization for hypersonic vehicle satisfying complex constrains[J].Chinese Journal ofAeronautics，2013，26（6）：1544-1553.

[6]袁宴波，张科，薛晓东.基于Radau伪普法的制导炸弹最优滑翔弹道研究[J].兵工学报，2014，35（8）：1179-1186.YUAN YANBO，ZHANG KE，XUE XIAODONG.Optimization of glide trajectory of guided bombs using a Radau Pseudo-spectral method[J].Acta Armamentarh，2014，35（8）：1179-1186.（in Chinese）

[7]胡锦川，陈万春.高超声速飞行器平稳滑翔弹道设计方法[J].北京航空航天大学学报，2015，41（8）：1464-1474.HU JINCHUAN，CHEN WANCHUN.Steady glide trajectory planning method for hypersonic reentry vehicle[J].Journal of Beijing University of Aeronautics and Astronautics，2015，41（8）：1464-1474.（in Chinese）

[8]MEASE K D，CHEN D T，SCHONENBEEGER H.Reduced-order entry trajectory planning for acceleration guidance[J].Journal of Guidance，Control and Dynamics，2002，25（2）：257-266.

[9]梁子璇，任章.基于在线气动参数修正的预测制导方法[J].北京航空航天大学学报，2013，39（7）：853-857.LIANG ZIXUAN，REN ZHANG.Predictive reentry guidance with aerodynamic parameter online correction[J].Journal of Beijing University of Aeronautics and Astronautics，2013，39（7）：853-857.（in Chinese）

[10]ZHAO J，ZHOU R，JIN X.Progress in reentry trajectory planning for hypersonic vehicle[J].Journal of Systems Engineering and Electronics，2014，25（4）：627-639.

[11]刘冠南，周浩，陈万春.高超声速飞行器再入多段导引方法研究[J].飞行力学，2012，30（4）：337-340.LIU GUANNAN，ZHOU HAO，CHEN WANCHUN.A study on the multiple-phase reentry guidance method of hypersonic vehicle[J].Flight Dynamics，2012，30（4）：337-340.

[12]陈小庆，侯中喜，刘建霞.高超声速滑翔飞行器弹道特性分析[J].导弹与航天运载技术，2011（2）：5-9.CHEN XIAOQING，HOU ZHONGXI，LIU JIANXIA.Trajectory characteristic of hypersonic gliding vehicle[J].Missile and Space Vehicles，2011（2）：5-9.（in Chinese）

[13]王俊波，田源，任章.基于最优化问题的混合再入制导方法[J].北京航空航天大学学报，2010，36（6）：736-740.WANG JUNBO，TIAN YUAN，REN ZHANG.Mixed guidance method for reentry vehicle based on optimization[J].Journal of Beijing University of Aeronautics and Astronautics，2010，36（6）：736-740.（in Chinese）

[14]侯明善，刘怀勋，张金鹏.中远程战术导弹复合制导的交换规律[J].电光与控制，1998，5（4）：14-17.HOU MINGSHAN，LIU HUAIXUN，ZHANG JINPENG.Shified law of compound guidance of medium and long range tactical missile[J].Electronics Optics and Control，1998，5（4）：14-17.（in Chinese）

[15]王延.近距空空导弹中末制导交接班策略研究[D].西安：西北工业大学，2006.WANG YAN.Study on closed-end air-to-air missile midcourse guidance turnover strategy[D].Xi’an：Northwestern Polytechnical University，2006.（in Chinese）

[16]周浩，陈万春，殷兴良.高超声速飞行器滑行轨迹优化[J].北京航空航天大学学报，2006，32（5）：513-517.ZHOU HAO，CHEN WANCHUN，YIN XINLIANG.Optimization of glide trajectory for hypersonic vehicle[J].Journal of Beijing University of Aeronautics and Astronautics，2006，32（5）：513-517.（in Chinese）

[17]王少平，董受全，葛津华.目标机动对高超声速反舰导弹下压段导引特性的影响分析[J].战术导弹技术，2017，（1）：55-61.WANG SHAOPING，DONG SHOUQUAN，GE JINHUA.Influence analysis of target maneuver on steering characteristic of hypersonic anti-ship missile dive phase[J].Tactical Missile Technology，2017，（1）：55-61.（in Chinese）

[18]呼卫军，周军.临近空间飞行器策略与拦截武器能力分析[J].现代防御技术，2012，40（1）：11-15.HU WEIJUN，ZHOU JUN.Analysis of the interception strategy of the near space vehicle and capability of the interception weapon[J].Modern DefenseTechnology，2012，40（1）：11-15.（in Chinese）