多飞航导弹目标协同跟踪技术研究

崔树林，张翔宇，张光轶

（1.北京239厂军代室，北京100000；2.海军航空大学，山东烟台264001）

多弹协同作战打破了传统的各飞航导弹之间没有任何联系的作战思想，将发射后的所有飞航导弹看作一个整体，通过不同飞航导弹的相互配合和使用，可有效实现对预定目标的精确打击[1]。这其中，一个核心的问题就是多飞航导弹对目标的精确跟踪。多飞航导弹对目标的精确跟踪既是实现目标精确打击的一个有效手段，又是现代化作战中目标制信息权获取的前提和关键。

为了有效实现多飞航导弹对目标的精确跟踪，文献[2]将不同飞航导弹攻击组网化，通过领弹和攻击弹的优化布站和协同配合，实现了导弹自身生存能力和目标跟踪精度的提高，但却没有考虑目标数较多的情况。在目标数较多的情况下，文献[3]结合博弈论的方法决策出任一目标的最佳飞航导弹组合，但却忽略了不同飞航导弹的目标量测是否源于同一目标的问题。针对这一情况，一种基于统计关联决策[4-5]的动平台[6-7]融合跟踪方法被有效提出。该方法可有效实现多飞航导弹对目标的精确跟踪，但其模型构建相对理想，并没有充分考虑地球曲率[8-10]对目标跟踪的影响。而在实际过程中，地球曲率不仅存在，且严重影响着多飞航导弹对目标的定位跟踪精度。

为有效解决这一问题，目前一般采用ECEF坐标系[11]下的KF[12]、EKF[13]跟踪技术。但是，在 ECEF 坐标系下的目标跟踪中，由于坐标转换的高度非线性，ECEF坐标系下的目标的量测、特别是其协方差中不可避免地会存在较大的旋转平移误差[14]，进而导致跟踪误差的积累，产生滤波发散[15-18]。

针对上述问题，本文在时空协同的基础上，提出一种基于弹载雷达组网的无偏不敏自适应融合跟踪算法，以实现多飞航导弹对目标定位跟踪精度的提高。

1 多弹协同组网跟踪模型

多弹组网跟踪模型如图1所示。

图1 多弹组网跟踪模型图Fig.1 Motion model of multiple missiles network tracking

假设在收到攻击指令后，n枚飞航导弹共同向目标活动区域运动。不同飞航导弹按作战指令要求在空中快速组网，形成一个多弹协同组网跟踪系统。其中，高弹道飞行的飞航导弹承担领弹任务，并指定其中1枚飞航导弹为主领弹（网络中心节点），1～2枚飞航导弹为备份主领弹。各领弹在开机后对目标活动区域进行扇形覆盖搜索。当发现目标时，主领弹通过数据链将目标信息和攻击指令传递给位于低弹道飞行的攻击弹。在接收到主领弹攻击指令后，不同频段、不同类型的攻击弹同时开机，以配合领弹网对目标进行协同精确跟踪。这时，即使敌方对某一频率、某一攻击方向上的飞航导弹能够进行有效干扰，但却来不及对其他频率、其他攻击方向上的飞航导弹进行有效的干扰。由此可见，多弹协同组网可大大提高飞航导弹的突防能力和电子对抗能力。

2 多弹协同时空同步模型

在对不同飞航导弹进行组网布站的基础上，各飞航导弹须在时间和空间上进行同步，实现各飞航导弹间信息的共享。

2.1 空间协同

2.1.1 ECEF坐标系下的空间协同

要实现不同飞航导弹间信息的共享，首先要对目标进行空间上的协同，将各飞航导弹的信息集中到一个统一的坐标系。

ECEF坐标系就是一种典型的惯性坐标系，以ECEF坐标系为融合中心可有效实现对目标的融合跟踪，其具体流程如图2所示。

图2 多飞航导弹空间协同示意图Fig.2 Space cooperation of multiple cruise missiles

假设k时刻第i(i=1,2,…)枚飞航导弹的对目标的量测为Zi(k)=[ri(k),θi(k),φi(k)]T，且其受到0均值、恒定方差的高斯量测噪声的影响。

为实现对目标的线性化跟踪，NED坐标系下的目标量测可对应表示为：

式（1）中：；f1为弹载极坐标到NED坐标的无偏转换函数。

在获得目标NED量测的基础上，ECEF坐标系下的目标量测可对应表示为：

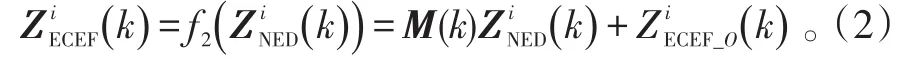
式（2）中：f2是NED坐标到ECEF坐标的转换函数；M(k)表示NED坐标到ECEF坐标的旋转矩阵；分别为ECEF坐标系下导弹i和目标的位置量测。

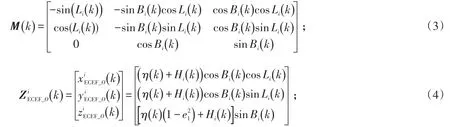
式（3）～（5）中：[Li(k),Bi(k),Hi(k) ]为导弹i的地理位置信息；a为地球长半轴；为第一偏心率。

2.1.2 基于UT变化的ECEF量测预处理

由于坐标转换的高度非线性，以及旋转平移变换的影响，ECEF坐标系下的目标量测不可避免地会存在较大的量测转换误差。特别在对量测协方差的获取中，该误差的影响尤其严重。针对这一情况，拟采用UT变换的方法以有效解决这一问题。

假定：

为导弹i的极坐标量测到ECEF坐标量测的综合转换过程，并在此基础上选取弹载极坐标量测Zi(k)的2L+1个δ采样点χj：

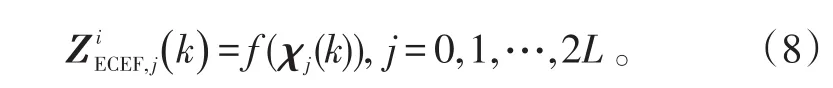
进而ECEF坐标系下的目标量测及其协方差可对应表示为：

式（7）～（10）中：λ=α2(L+κ)-L，α决定δ采样点的散布程度，通常取一小的正值（如0.01），κ通常取0，L为量测向量的维数；Ri(k)为极坐标系下的初始量测协方差；w0=λ/(L+λ)；wj=1/[2(L+λ)]，j=0,1,…,2L。

2.2 时间协同

由于不同飞航导弹所获得的目标信息不可能始终同步，为此以精度高的飞航导弹为基准，对各飞航导弹的目标观测数据进行内插外推，将低精度的观测数据推算到高精度的观测时间点上，以达到不同飞航导弹时间上的同步，其具体如图3所示。

图3 多飞航导弹时间协同示意图Fig.3 Time cooperation of multiple cruise missiles

协同后的低精度量测ZLH及时间协同速度VH分别为：

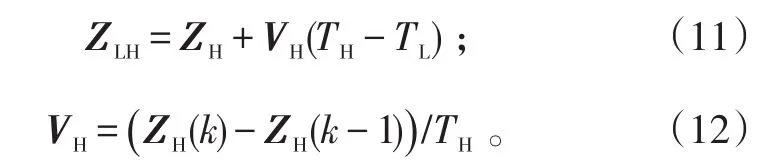
式（11）、（12）中：ZH为高精度量测；TL和TH分别为低精度量测和高精度量测所对应的时间。

3 多弹协同融合跟踪模型

3.1 目标状态估计

在对各飞航导弹量测预处理的基础上，令

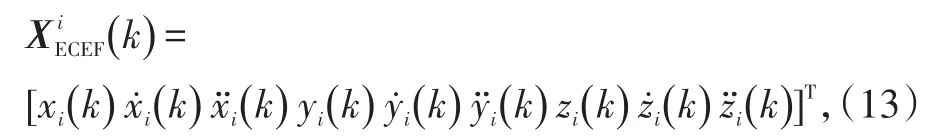
则利用无偏Kalman滤波的方法就可有效获得不同飞航导弹对目标的定位跟踪。假设k时刻第i枚飞航导弹对目标的状态估计和协方差分别为和，则其状态和协方差的一步预测可对应表示为：

本文将在系统识别干旱危害机制及成因的基础上，分析我国干旱特征及发展趋势，并剖析我国在抗旱减灾中存在的问题，进而提出我国干旱综合应对在从“危机管理”向“风险管理”转变的同时，还应在构建物理机制统一的水资源及伴生过程模拟平台的基础上建立干旱风险评价指标体系，为综合应对变化环境下我国的干旱问题提供依据。

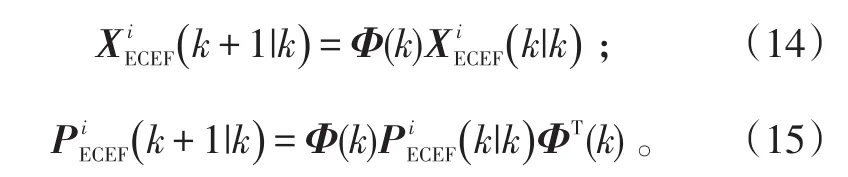
式（14）、（15）中：Φ(k)、Φ1(k)为状态转移矩阵，且

对应地，量测的预测：

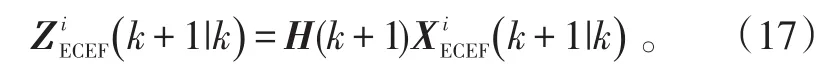
新息及其协方差：

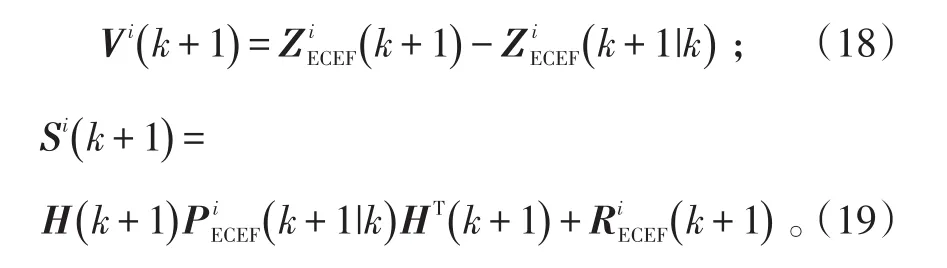
增益：

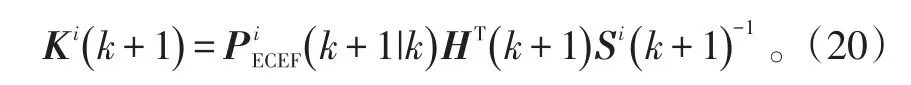
状态和协方差更新：

3.2 自适应融合跟踪

在各飞航导弹对目标有效跟踪的条件下，假定任意2枚飞航导弹对目标的状态估计及其协方差分别为XECEF_1(k)、PECEF_1(k)和XECEF_2(k)、PECEF_2(k)，拟通过自适应融合跟踪的方法来进一步提高多飞航导弹对目标的定位跟踪精度，其具体步骤如下。

1）判断2条航迹的统计距离是否在正常范围内。利用统计距离

和门限T1进行比较。如果S1＜T1，说明2条航迹来自于同一目标，则采用最优加权航迹融合算法进行航迹融合。

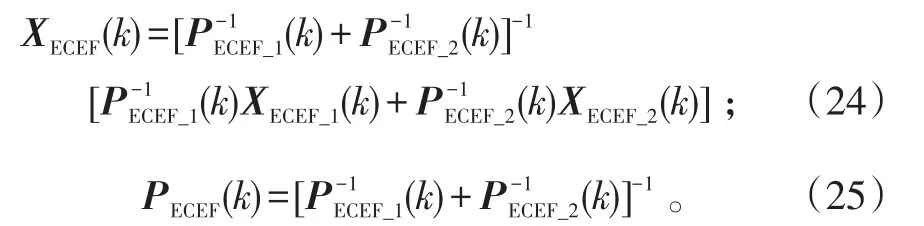
式（24）～（25）中：T1服从自由度为n1的χ2分布；n1为状态向量XECEF(k)的维数。

2）如果T1≤S1＜T2，说明2条航迹来自同一目标，但2条航迹的跟踪精度相差较大，则利用距离测度

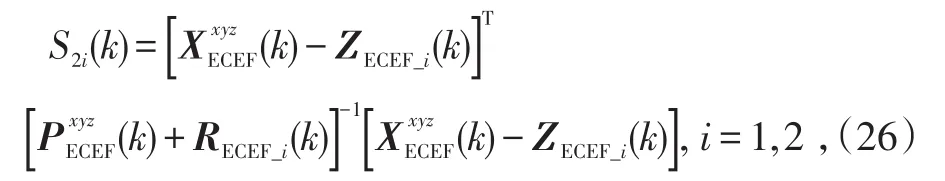
相比较来选取距离测度S2i(k)较小的航迹为融合航迹。

3）当S1≥T2，说明2条航迹不是来自于同一个目标，则分别输出。对分别输出的航迹，将其量测值与航迹的距离

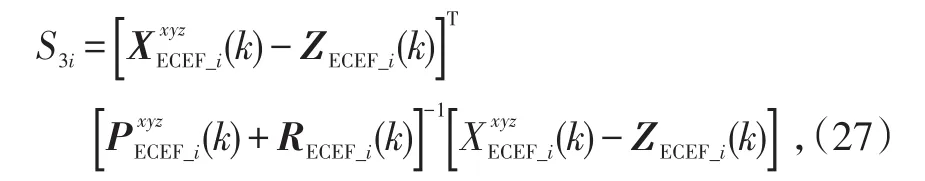
和门限T3相比较。如果S3i＞T3，则说明航迹发散，输出位置用量测值，输出速度用前n个时刻的平均；反之，则说明航迹正常，取其航迹为输出航迹。其中，T3服从自由度为n2的χ2分布，n2为量测向量ZECEF(k)的维数。

当所获得的飞航导弹航迹数m≥3时，首先，按照上述自适应融合跟踪的方法，先对前2条航迹进行融合跟踪处理，再重新将所得航迹和第3条航迹作为自适应融合跟踪的输入，已获得更加精确的目标航迹，对于第i=4,5,…,N条航迹，以此类推处理。

4 仿真分析与结论

为验证本文所提的基于弹载雷达组网的无偏不敏自适应融合跟踪算法的有效性，对多飞航导弹目标融合跟踪的问题进行了仿真，并分别与文献[2-3，5]中的多传感器多目标跟踪算法进行对比试验。

4.1 仿真参数设置

假定我方2枚领弹和3枚攻击弹共同对目标进行跟踪拦截，导弹和目标的真实轨迹在地理坐标系下建模，跟踪在ECEF坐标系下进行。其中，2枚领弹的初始位置分别为 [44°,108°,5km]和 [44°,108.2°,5km]，3枚攻击弹的初始位置分别为 [44°,108°,2km]、[44°,108.2°,2km]和 [44°,108.4°,2km]，且以 Ma=2 的速度向目标区域运动。目标的初始位置为[44.5°,108.2°,15m]，并以人字形编队的形式沿北偏西45°的方向匀速直线运动，目标数为5，其速度大小为15 m/s。弹载雷达的测量精度为 [15 m,0.2°,0.2°]，GPS定位误差为2 m，姿态角误差为0.2°，惯导漂移误差为1km/20min。仿真时间60 s，其中搜索扫描阶段30 s，搜索扫描周期1.5 s，跟踪阶段30 s，跟踪周期0.02 s。在上述条件下，进行100次monte-carlo仿真。

4.2 仿真结果与分析

1）首先，为验证本文所提算法的有效性，将其与文献[2-3，5]中的多传感器多目标融合跟踪算法进行比较分析，其仿真结果如图4～17所示。其中，图4、5分别为杂波环境下人字形编队目标的量测及其跟踪结果。

图4 目标量测图Fig.4 Target measurements

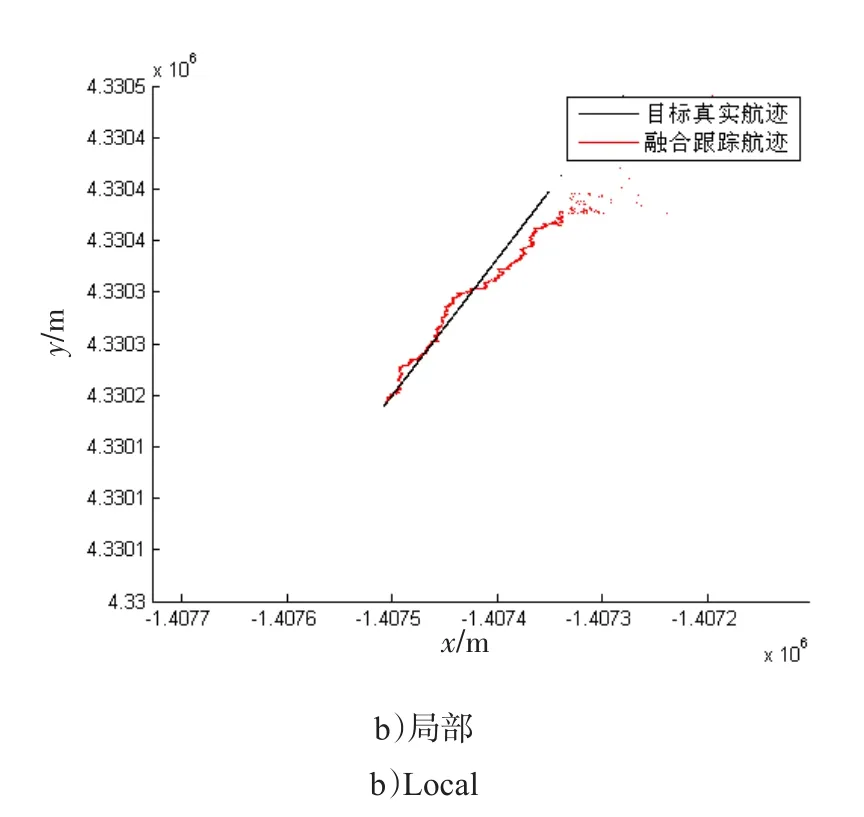
图5 目标融合跟踪图Fig.5 Tracking trajectory

由图4、5可以看出，在杂波环境下，本文提出的基于弹载雷达组网和GPS/INS组合导航的无偏不敏自适应融合跟踪算法可有效实现对人字形编队目标的融合跟踪。

图6～8为本文所提算法与文献[2]中多传感器简单组网布站时的跟踪比较图。

图6 目标距离误差跟踪图Fig.6 Target range estimation error

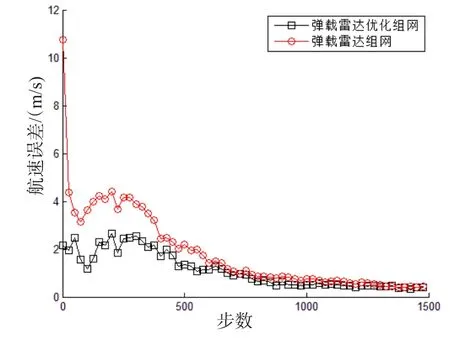
图7 目标航速误差跟踪图Fig.7 Target velocity estimation error

图8 目标航向误差跟踪图Fig.8 Target course estimation error

由图6～8可以看出，多飞航导弹目标跟踪误差呈逐渐收敛的趋势变化，且与弹载雷达简单组网的情况相比，本文所提算法具有较小的估计误差，并在距离和航向估计上的优势较为明显。

图9～11为本文所提算法与文献[3]中多传感器有偏转换时的跟踪比较图。

图9 目标距离误差跟踪图Fig.9 Target range estimation error

图10 目标航速误差跟踪图Fig.10 Target velocity estimation error

图11 目标航向误差跟踪图Fig.11 Target course estimation error

由图9～11可以看出，通过对目标量测的无偏不敏转换，本文所提算法对目标的距离、航速和航向跟踪精度都有较为明显的提高。

图12～14为本文所提算法与文献[5]中多传感器加权航迹融合时的跟踪比较图。由图12～14可以看出，与加权航迹融合算法相比，本文所提算法可进一步减小目标的距离、航速和航向估计误差。

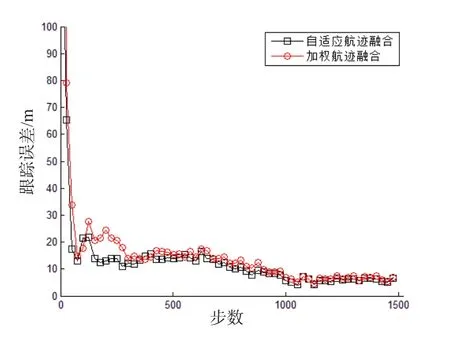
图12 目标距离误差跟踪图Fig12 Target range estimation error

图13 目标航速误差跟踪图Fig.13 Target velocity estimation error

图14 目标航向误差跟踪图Fig.14 Target course estimation error

5 结论

本文提出一种基于弹载雷达组网和GPS/INS组合导航的无偏不敏自适应融合跟踪算法。该算法通过领弹和攻击弹的优化布站，有效提高了多弹协同跟踪系统的定位跟踪精度和突防能力，并利用无偏不敏转换对目标量测的预处理，进一步减小了因旋转、平移和线性化误差所带来的影响；同时，在统计双门限判决机制的基础上，利用自适应融合跟踪算法来进一步实现了目标协同跟踪精度的提高。仿真结果表明，与现有的多弹协同目标跟踪算法相比，该算法具有较高的目标定位跟踪精度。

[1]王晓芳，洪鑫，林海.一种控制多弹协同攻击时间和攻击角度的方法[J].弹道学报，2012，24（2）：1-5.WANG XIAOFANG，HONGXIN，LIN HAI.A method of controlling impact time and impact angle of multiple-missiles cooperative combat[J].Journal of Ballistic，2012，24（2）：1-5.（in Chinese）

[2]王君，张蓬蓬，梁文波，等.多弹协同攻击网络化作战系统体系结构研究[J].航空兵器，2011（6）：10-14.WANG JUN，ZHANG PENGPENG，LIANG WENBO，et al.Research on system structure about multiple missiles cooperative attacking net combat system[J].Aero Weaponry，2011（6）：10-14.（in Chinese）

[3]刘钦，刘铮，刘俊.一种多机动目标协同跟踪的博弈论算法[J].西安电子科技大学学报，2012，39（6）：50-54.LIU QIN，LIU ZHENG，LIU JUN.Collaborative tracking algorithm for multiple maneuvering targets based on the game theory[J].Journal of Xidian University，2012，39（6）：50-54.（in Chinese）

[4]AKEILA EHAD，SALCIC ZORAN，SWAIN AKSHYA.Reducing low-cost INS error accumulation in distance estimation using self-resetting[J].IEEE Transactions on Instrumentation and Measurement，2014，63（1）：177-184.

[5]SONG ENBING，XU JIE，ZHU YUNMING.Optimal distributed kalman filtering fusion with Singular covariances of filtering errors and measurement noises[J].IEEE Transactions onAutomatic Control，2014，59（5）：1271-1282.

[6]WANG GUOHONG，CHEN LEI，JIA SHUYI.Optimized bias estimation model for 3-D radar considering platform attitude errors[J].IEEE Transactions on Aerospace and Electronic Systems，2012，27（1）：19-24.

[7]崔亚齐，熊伟，何友.基于MLR的动平台传感器误差配准算法[J].航空学报，2012，33（1）：118-128.CUI YAQI，XIONG WEI，HE YOU.Mobile platform sensor registration algorithm based on MLR[J].Acta Aeronautica et Astronautica Sinica，2012，33（1）：118-128.（in Chinese）

[8]董云龙，何友，王国宏.基于ECEF的广义最小二乘误差配准技术[J].航空学报，2006，27（3）：463-467.DONG YUNLONG，HE YOU，WANG GUOHONG.Generalized least squares registration algorithm with earthcentered earth-fixed（ECEF）coordinate system[J].Acta Aeronautica et Astronautica Sinica，2006，27（3）：463-467.（in Chinese）

[9]JENKINS KARAN，CASTANON DAVID.Informationbased Adaptive Sensor Management for Sensor Networks[C]//Proceedings of American Control Conference.San Francisco,California，2011：4934-4940.

[10]JIN XIAOBIN，DU JINJIN，BAO JIANG.Maneuvering target tracking by adaptive statistics model[J].The Journal of China Universities of Posts and Telecommunications，2013，20（1）：108-114.

[11]CHEN LEI，WANG GUOHONG，JIA SHUYI，et al.Attitude bias conversion model for mobile radar error registration[J].The Journal of Navigation，2012，65（4）：651-670.

[12]THURAIAPPAH SATHYAN，TAT JUNCHIN，SANJEEV ARULAMPALAM，et al.A multiple hypothesis tracker for multitarget tracking with multiple simultaneous measurements[J].IEEE Journal of Selected Topics in Signal Processing，2013，7（3）：448-459.

[13]LI YANGMING，LI SHUAI，SONG QUANJUN，et al.Fast and robust data association using posterior based approximate joint compatibility test[J].IEEE Transactions on Industrial Informatics，2014，10（1）：331-338.

[14]CARLOS RELBLANCO，FERNANDO JAUREGUIZA，NARCISO GARCAL.Inference of complex trajectories by means of a multibehavior and multiobject tracking algorithm[J].IEEE Transactions on Circuits and Systems for Video Technology，2013，23（8）：1300-1310.

[15]HE XIAOFAN，THARMARASA R，KIRUBARAJAN T.Modified murty’s algorithm for diverse multitarget top hypothesis extraction[J].IEEE Transactions on Aerospace and Electronic Systems，2013，49（1）：603-609.

[16]XU ZHENGHONG，LI YIN，RIZOS CAROL，et al.Novel hybrid of LS-SVM and Kalman filter for GPS/INS integration[J].The Journal of Navigation of Rin，2010，63（2）：289-299.

[17]QI LIN，HE YOU，DONG KAI.Multi-radar anti-bias track association based on the reference topology feature[J].IET Radar Sonar and Navigation，2018，12（3）：366-372.

[18]YUAN TING，KRISHNAN KRISHANTH，CHEN QICHOU.An IMM-based track association approach with sequential multiple hypothesis test[J].IEEE Transactions on Intelligent Transportaion Systems，2017，18（12）：3501-3512.