扁平型水下滑翔器水动力特性及滑翔性能研究
2019-12-02肖冬林王习建徐令令张安通
肖冬林,张 华,王习建,王 健,徐令令,张安通
(中国船舶科学研究中心,江苏 无锡 214082)
0 引言
水下滑翔器是一种通过剩余浮力做功提供前进动力,通过内部滑块移动进行姿态调节,从而实现垂直面内锯齿形运动的新型无人水下航行器。它有着工作时间长、工作范围广、能耗低、噪音低等诸多优点,在海洋环境监测、水下探测、通信等领域有着重要的应用价值[1]。
续航力是水下滑翔器的重要性能指标,为了提高水下滑翔器的航程,需要降低能耗,提高滑翔效率。滑翔器的滑翔效率与水动力外形、滑翔姿态、剩余浮力大小、搭载仪器功耗等诸多因素有关。文献[2]研究了不同类型滑翔器的运动状态、剩余浮力大小等对滑翔器滑翔效率的影响;文献[3]从做功的角度研究了滑翔姿态对滑翔器滑翔效率的影响;文献[4]分析了机翼展弦比、后掠角对升阻比的影响。以上文献在分析滑翔效率时均没有综合考虑水平速度。为了使水下滑翔器具有一定的机动性能及抵抗海流能力,水平滑翔速度也是一种重要的滑翔性能指标。
通常的水下滑翔器主体采用回转型,主要依靠滑翔翼调节水动力中心,有效载荷量相对较低。扁平构型主体具有升阻比高、有效载荷大的优势,是中大型远程水下滑翔器的重要发展方向。
本文采用单位重量滑翔器、单位水平速度所耗功率作为滑翔效率的评价指标,研究了扁平型水下滑翔器的滑翔运动特性,给出了滑翔效率最高的滑翔姿态,并进行了垂直面滑翔运动仿真。
1 水下滑翔器滑翔特性分析
1.1 受力分析
对滑翔器垂直面定常滑翔状态进行受力分析,如图1所示。其中:D表示阻力;L表示升力;M表示滑翔器受到的俯仰力矩水动力;α表示攻角;ξ表示滑翔角,即速度与水平方向的夹角;m0g表示剩余浮力;坐标原点O位于均衡态滑翔器的浮心。

图1 水下滑翔器受力分析Fig.1 Force analysis of underwater glider
受力平衡需满足:
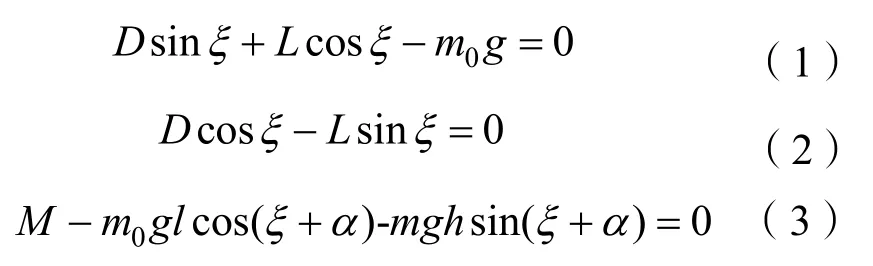
式中:l表示剩余浮力作用中心到坐标原点O的距离;h表示稳心高;m表示滑翔器质量。滑翔器水动力系数无论滑翔模式或动力推进模式均可以按下式进行简化[5]:
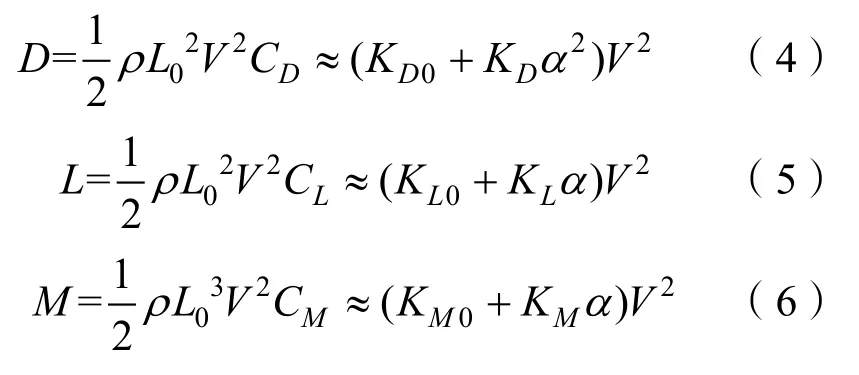
式中:ρ表示海水密度;L0表示滑翔器总长;CD、CL、CM分别表示无因次的阻力系数、升力系数及俯仰力矩系数;KD、KL等表示滑翔器的水动力系数,可认为是常数。
1.2 滑翔效率指标
从能耗的角度研究滑翔器的续航力,本文采用的指标为单位重量水下滑翔器移动单位水平距离所需能耗[6]:
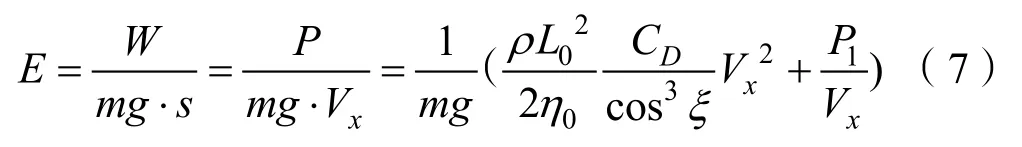
式中:E表示能耗系数;W表示重量为mg的滑翔器水平移动距离为S时的总能耗;Vx表示平均水平速度;P表示平均功率,包括浮力调节系统平均功率P0;姿态调节系统、传感器等搭载仪器及通信系统平均功率P1。
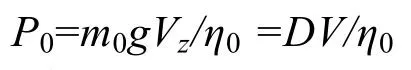
式中:m0g表示平均剩余浮力大小;Vz表示平均垂直速度大小;η0表示剩余浮力调节系统机械效率。
显然,能耗系数E越小,水下滑翔器滑翔效率越高。
由式(2)、(4)、(5)可得:
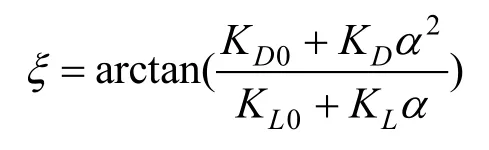
对于特定水下滑翔器,总长L0、η0、P1均可认为是定值。忽略雷诺数的影响,式(7)中阻力系数CD及滑翔角ξ可认为仅与滑翔姿态(攻角α)有关。因而能耗系数E与水平滑翔速度Vx及滑翔姿态(攻角α)有关。
式(7)括号中第 1项表示滑翔器克服水动力阻力的功耗,与滑翔姿态和水平滑翔速度有关;第2项表示滑翔器搭载仪器设备功耗,仅与水平滑翔速度有关。定义仅与滑翔姿态相关的滑翔效率函数f(α):

显然,f(α)越大,剩余浮力调节系统功耗越大,能耗系数越大。定义使f(α)在定义域内取得最小值的α为最优滑翔姿态攻角,最优攻角记为αP,再对式(7)求导,可得到使得E取得极小值最优水平速度Vxp:

得到了最优滑翔姿态及最优水平速度,并获取最优滑翔状态下的水动力。根据受力平衡方程(1)-(3)可得到水下滑翔器的设计最优剩余浮力m0g及相应的剩余浮力力臂l或稳心高h。
本文研究的问题是相同水平速度下,不同姿态角的滑翔效率。
2 扁平型水下滑翔器水动力特性计算分析
2.1 水动力CFD计算及试验验证
本文研究的扁平型水下滑翔器水动力外形主要由主体、滑翔翼及艉操纵面组成。主体为长3.7 m、最大宽度0.76 m、最大高度0.35 m的扁平形体,滑翔翼展长2.1 m。
采用商用CFD计算软件STAR CCM+对扁平型水下滑翔器进行了操纵性水动力仿真计算。计算网格采用六面体网格,计算域为艇首向前1.5倍艇长,艇尾向后3倍艇长,周向2倍艇长。网格数量约150万,艇体表面y+取50。[7]
计算速度2 kn(雷诺数Re=3.52×106),不同攻角下,垂向力系数Z′及俯仰力矩系数M′与风洞试验结果比较见图2。风洞试验模型缩尺比1∶1.2,试验模型与滑翔器满足雷诺数相似,试验风速对应滑翔器水中航速为1.028 8 m/s。
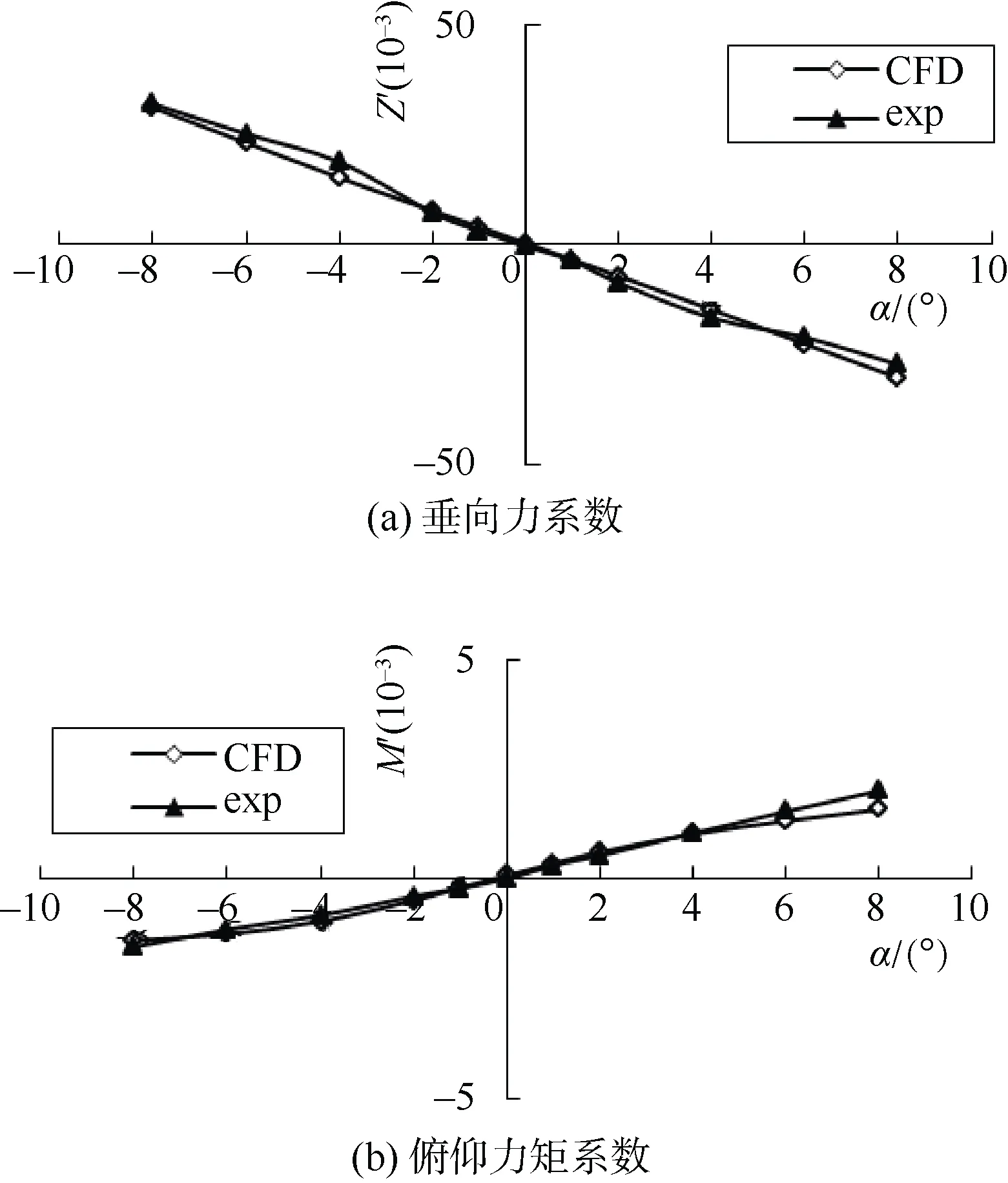
图2 计算结果与试验结果对比Fig.2 Comparison of CFD results with experimental results
计算结果与试验结果吻合较好,由小角度回归得到的位置导数Zw′相对误差4.1%,Mw′相对误差14.6%。Mw′相对误差偏大,这主要是因为航速较低、水动力中心位置靠近潜航器中心,小攻角下俯仰力矩绝对值较小。整体上计算误差在可接受范围内,因此计算位置导数所采用的数值计算方法是可信的。
2.2 扁平型水下滑翔器水动力特性
通过系列 CFD计算,得到了扁平型水下滑翔器水动力系数KD0、KD、KL0、KL、KM0、KM。
得到水动力系数后,根据式(4)-(6)可得到升阻比λ(λ=L/D)随攻角α的变化曲线。
由图3可知,扁平型水下滑翔器最大升阻比约为6.4,对应的攻角约8.10°。传统回转体构型的水下滑翔器即使在搭载了高展弦比滑翔翼的情况下,最大升阻比只能达到5左右[8]。本文研究的扁平型水下滑翔器较传统回转型水下滑翔器具有更大的最大升阻比。
3 滑翔性能计算及运动仿真
3.1 滑翔性能计算
据式(1)-(8)可得到f(α)随攻角α的变化曲线,见图4。
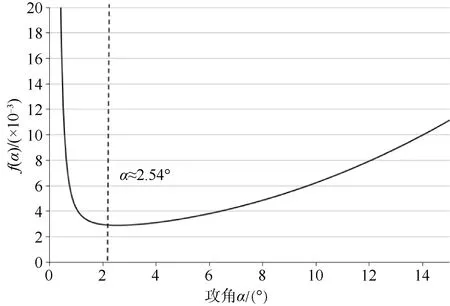
图4 f(α)-攻角曲线Fig.4 Curve of f(α)-attack angle
由图4可知,扁平型水下滑翔器最优滑翔姿态攻角约为2.54°。根据f(α)随攻角α的变化曲线,要使剩余浮力做功较最优滑翔角增幅10%以内,则扁平型水下滑翔器设计攻角范围应为1.54°~4.27°,对应的滑翔角范围为10.8°~23.8°;要使剩余浮力做功较最优滑翔角增幅5%以内,则扁平型水下滑翔器设计攻角范围应为1.75°~3.73°,对应的滑翔角范围为 11.7°~21.3°。
由式(1)-(6)可得到水平滑翔速度为
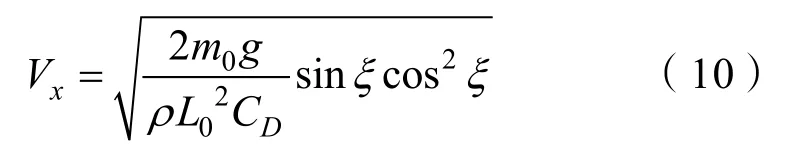
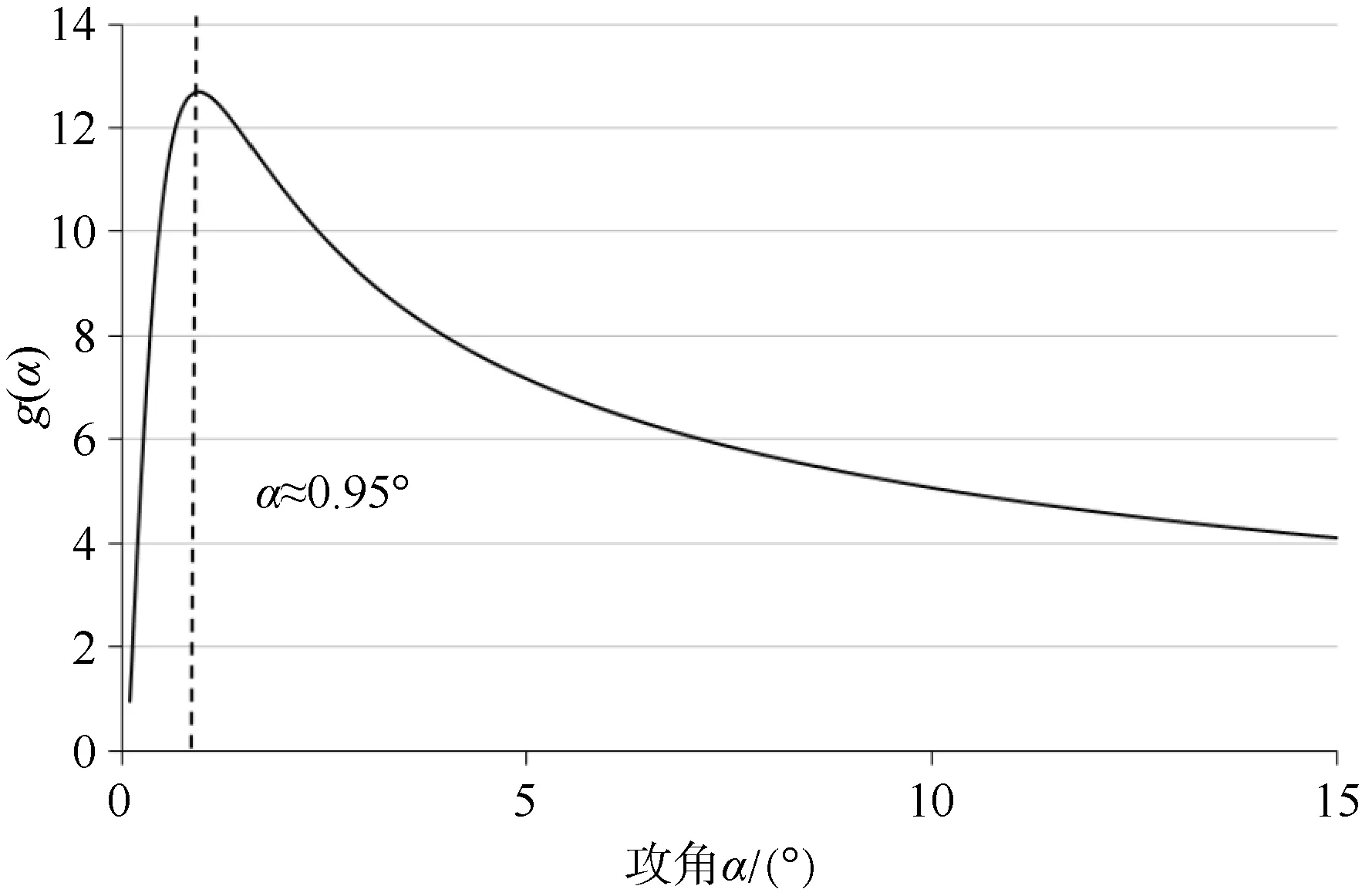
图5 g(α)-攻角曲线Fig.5 Curve of g(α)-attack angle
由图5可知,当攻角约为 0.95°时,扁平型水下滑翔器水平滑翔速度最大。
假定设计水平滑翔速度为0.77 m/s,则在水平速度最大的滑翔姿态(α≈0.95°)、最优滑翔姿态(α≈2.54°)、升阻比最大的滑翔姿态(α≈8.10°)3种滑翔状态下,对应的设计剩余浮力及滑翔运动参数如表1所示。
根据表1,结合式(7),以相同水平滑翔速度运动,升阻比最高的滑翔姿态(α≈8.10°)较最优滑翔姿态(α≈2.54°)剩余浮力做功增大约70%,水平速度最大的滑翔姿态(α≈0.95°)则较最优滑翔姿态(α≈2.54°)剩余浮力做功增大约54%。
3.2 滑翔运动仿真计算研究
由式(1)-(3)可知,对于水动力外形一定的水下滑翔器,可以通过改变剩余浮力力臂或稳心高来调节滑翔姿态角。通过设置不同的剩余浮力及稳心高,对3种典型滑翔状态进行仿真计算。仿真计算模型采用六自由度操纵运动数学模型,根据扁平型水下滑翔器的水动力特性对数学模型进行了适当简化。
3.2.1 不考虑环境因素改变的运动仿真
不考虑海水密度随深度的变化及艇体压缩等导致剩余浮力变化,对水平滑翔速度最大的滑翔状态、最优滑翔状态及升阻比最高的滑翔状态3种典型滑翔姿态进行了2 000 m滑翔运动仿真。
不同滑翔姿态,仿真计算得到的单周期运动参数如表2所示。
表2中单周期深度差△Ze表示下潜最大深度和上浮最小深度之差。不同滑翔姿态下平均水平滑翔速度略有差异,是由于受到了转换段的影响。单周期剩余浮力做功W0=2m0g△Ze/η0。

图6 最优滑翔姿态滑翔运动仿真结果(m0g = 43.3 N)Fig.6 Simulation results of optimal gliding attitude(m0g= 43.3 N)

表2 典型状态滑翔运动仿真结果Table 2 Simulation results of typical gliding attitudes
假定剩余浮力调节系统机械效率η0=0.4,扁平型水下滑翔器质量650 kg,则不同滑翔姿态下单周期剩余浮力做功、仅考虑剩余浮力做功的能耗系数E0及根据式(7)-(8)得到的f(α)的比较如表3所示。

表3 典型状态滑翔运动效率分析Table 3 Gliding efficiency analysis of typical gliding attitudes
仿真结果表明,最优滑翔姿态下,单位水平距离浮力调节系统做功远低于水平滑翔速度最大滑翔姿态及升阻比最大的滑翔姿态。
3.2.2 考虑环境因素的运动仿真
随着下潜深度的变化,由于海水密度变化及艇体压缩,水下滑翔器受到的剩余浮力会产生变化。海水密度随深度的变化特性采用中国南海典型海域实测数据[9]。滑翔器艇体排水体积变化量近似认为随海水深度线性变化,根据有限元分析结果,艇体排水体积随深度的变化量d▽可表示成如下形式:

根据有限元分析结果,k可取为1.56×10-6。
设定剩余浮力43.3 N,考虑海水密度变化及艇体压缩的2 000 m滑翔运动仿真结果如图7所示。
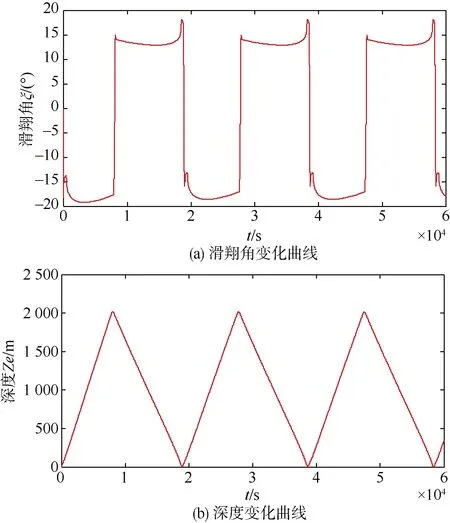
图7 考虑环境因素的最优滑翔姿态滑翔运动仿真结果(m0g = 43.3 N)Fig.7 Simulation results of optimal gliding attitude considering environmental factors(m0g= 43.3 N)
仿真结果表明:下潜滑翔角为 13.2°~18.6°,上浮滑翔角12.9°~18.1°,深度差△Ze=2 013.2 m,单周期水平滑翔距离 14 759 m,单周期时间为19 719 s,平均水平滑翔速度0.748 m/s。计算得到f(α)为 3.08,较不考虑环境因素的仿真结果略有增大,这是由于滑翔角大都处在滑翔效率较优的范围内。
4 结束语
本文采用单位重量滑翔器、单位水平速度所耗功率作为滑翔效率的评价指标,研究了扁平型水下滑翔器的滑翔运动特性,得到了如下结论:
1)本文采用CFD方法获取了扁平型水下滑翔器操纵性水动力系数,CFD计算结果与风洞试验结果符合良好;
2)本文研究的扁平型水下滑翔器最大升阻比为6.4,大于传统回转型主体的水下滑翔器;
3)基于本文滑翔效率评价指标得到的最优滑翔姿态攻角约 2.54°,相同水平滑翔速度下,浮力调节系统功耗远低于水平滑翔速度最大的滑翔姿态及升阻比最高的滑翔姿态;
4)本文给出了扁平型水下滑翔器滑翔效率较优的滑翔姿态设计范围:剩余浮力做功较最优滑翔姿态增幅 5%、10%以内的攻角范围分别为1.75°~3.73°、1.54°~4.27°,对应的滑翔角范围分别为 11.7°~21.3°、10.8°~23.8°。
5)本文对扁平型水下滑翔器进行了典型滑翔姿态下的2 000 m滑翔运动仿真,仿真结果对滑翔性能分析结论进行了进一步验证。
