基于层次分析法的工程评标应用研究

王浩伟，谢栋明

（福建农林大学金山学院，福建 福州，350000）

0 引言

“综合评分法”和“经评审的最低评标价法”是目前国内各个工程项目招标过程中经常使用的两种评标方法。但这两种评标方法主要是根据一定比例的权重判定投标人，因此无法避免现实评标过程中所存在的一系列客观问题[1-6]。由于造成最终结果不公平的主要因素是人为干扰，所以在建筑工程评标过程中使用层次分析法可有效的减少了人为因素的干扰[7-12]。科学客观的筛选出投标人，这不仅是对传统的评标方法进行升级优化，而且对最终的评标结果起到直接的影响，相比于以上两种方法，应用层次分析法所产生的结果显得更加客观严谨。本文基于层次分析法的实际应用，对工程评标进行科学的应用和判定。

1 建立工程评标体系

1.1 工程评标的评价指标

（1）工程报价

总报价：总报价指的是承包商即投标方通过前期的计算等工作，确定要承包该项工程的总价格。

（2）施工进度方案

施工前提准备工作：施工前期准备工作的内容包括：技术准备，即对图纸检查并熟悉、平整场地、临水临电的设置、办理施工许可证等。

建设资金施工及时到位：建设资金能否及时到位，关系到对项目建设初期阶段的投资决策、经济评价。能够及时到位对工程顺利时候是有好处的。

第三方延误：第三方延误指的是不属于甲乙双方的原因而造成的延误情况，对施工进度是有负面影响的。

人材及施工设备到位情况：人材及施工设备应按照施工进度流程表提前进场，这样能够有效保证施工的正常进度。

（3）企业信誉

企业业绩：企业业绩在很大一定程度上反映了企业的竞争力水平和自身的承包能力水平。企业业绩和企业信誉是一种相互影响的关系。

合同履约情况：合同履约情况是指合同双方对合同上约定的内容的完成情况。能否有效地履约合同影响了企业的信誉。

诉讼情况：企业诉讼记录反映了企业的信誉情况。

（4）安全质量体系

文明施工及环保：文明施工包括许多内容，例如现场应该有的安全措施、围挡以及控制扬尘等。安全管理体系：项目现场应具有完善的安全管理体系，进场人员应当接收安全交底，完成三级安全教育。

质量保证体系：项目现场应具有完备的质量保证体系，专人专管，对每一个分项分部工程的质量都进行严格检查，出现问题及时修正严重的可以勒令停工整顿。

1.2 构建工程评标指标模型

确定工程项目评标的指标因素并建立其工程评标指标体系，见表1。

表1 工程评标指标模型Table 1 Index model of project bid evaluation

2 基于层次分析法的工程评标实例分析

2.1 工程项目概况

工程名称：某公寓二期商品房工程。

招标人：福州市某房地产经营开发公司。

招标规模：25300 m2，包括1、2、3号楼、地下车库。三栋楼中，第1、2号楼的整体结构为地上18层，地下1层，占地面积为103111 m2，墙体结构为剪力墙结构；剩下的第3号楼结构为地上17层，地下1层，占地面积为12400 m2，墙体结构为剪力墙结构；地下车库为地下1层，3000 m2，框架结构。

承包方式：包工包料。

质量标准：国家质量验收合格标准。

工期：总工期450天（日历日）。

招标范围：招标人所发的所有内容，其中包括设计施工图纸、工程量清单。

招标方式：公开招标。

该建设项目招标进行资格预审后，通过的审核的合格投标人分别有：A、B、C三家投标单位，其投标文件符合招标文件上的要求。相应报价如表2所示：

表2 投标人情况表Table 2 Bidders' table

2.2 构造工程评标因素判断矩阵

通过对递阶层次结构图形分析，将较低层次的各个因素相对于他们隶属的上层次某个元素的重要程度进行了两两互相比较和对比，从而构建一级评价因素判断矩阵[13-15]。判断矩阵如下：

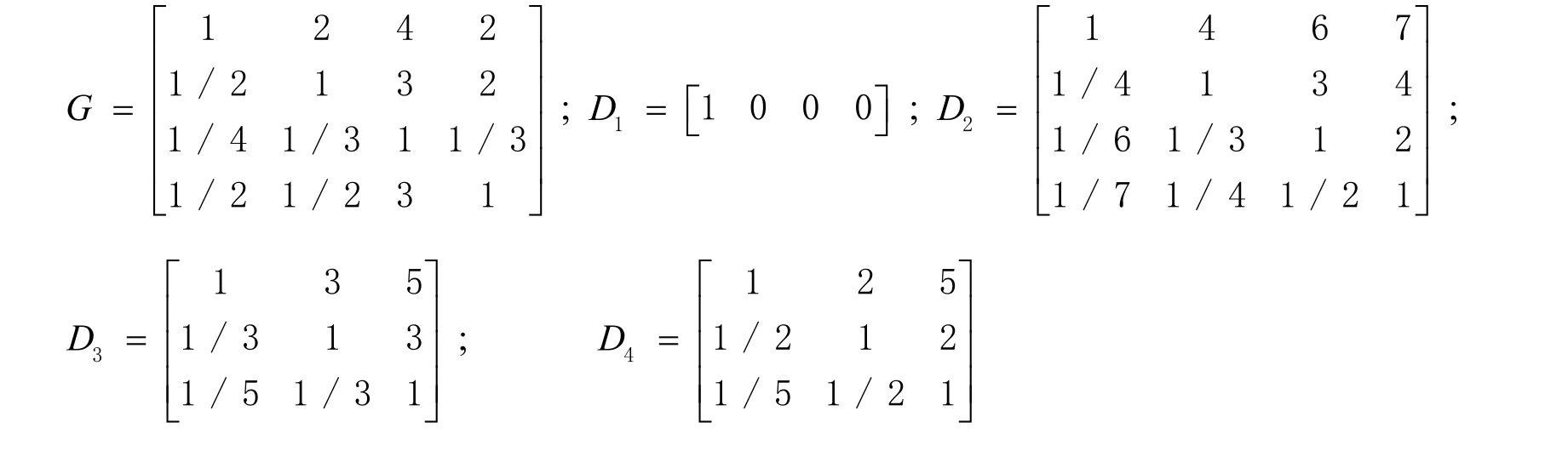
2.3 计算指标权重

（1）计算判断矩阵的特征向量及对应特征值

计算判断矩阵最大特征值对应的特征向量，利用求根法公式求得：

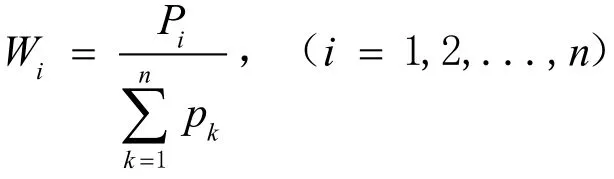
w1= 0.4297， w2= 0.2827， w3= 0.0877， w4= 0.1999。

所求特征向量 W= (0 .4297,0.2827,0.0877,0.1999)，用特征向量W计算判断矩阵的最大特征值，即: λmax= 4.0812。

（2）计算判断矩阵D2、D3、D4的特征向量及对应特征值

计算判断矩阵D2最大特征值对应的特征向量，得：

进行归一化处理，得到特征向量W，即：

所求特征向量 W2= (0 .6145,0.2246,0.0985,0.0624)，用特征向量W计算判断矩阵的最大特征值，即 λmax2= 4.1021。

同理： 对于判断矩阵D3的最大特征值用相对应的特征向量表示出来，即 W3= (0 .6370 0.2583 0.1047)，得出最终最大特征值 λmax3= 3.0385。

对于判断矩阵D4的最大特征值用相对应的特征向量表示出来，即 W4= (0 .5954 0.2764 0.1283)，得出最终最大特征值 λmax4= 3.0055。

2.4 层次单排序和总排序一致性检验

（1）对判断矩阵进行一致性检验

通过查下表3可得， RI= 0.9。

表3 一致性指标的取值Table 3 The value of the consistency index RI

因此判断矩阵G−D满足一致性检验要求。

（2）对判断矩阵D2、D3、D4进行一致性检验

分别对判断矩阵D2、D3、D4进行一致性检验，具体计算过程如下：

对D2进行一致性检验

因此D2矩阵满足一致性检验要求。

同理：

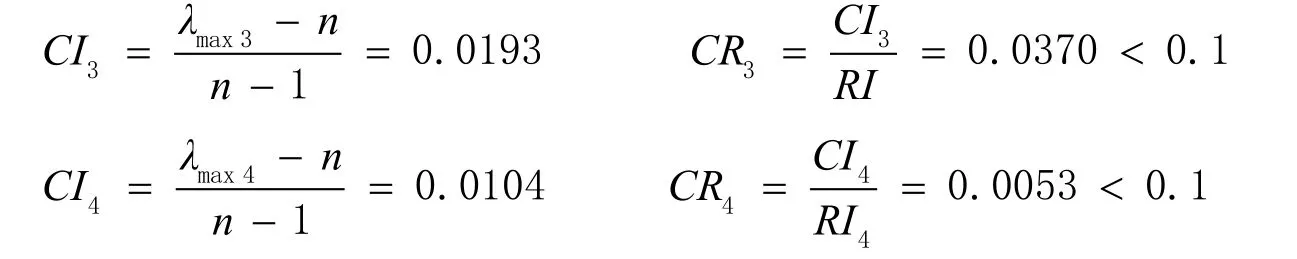
因此D2、D3、D4矩阵都满足一致性检验要求。

（3）一致性检验层次的总排序情况

当 CR＜ 0.1时，层次总排序的结果可以确定是有满意的一致性。层次总排序表如表4所示：

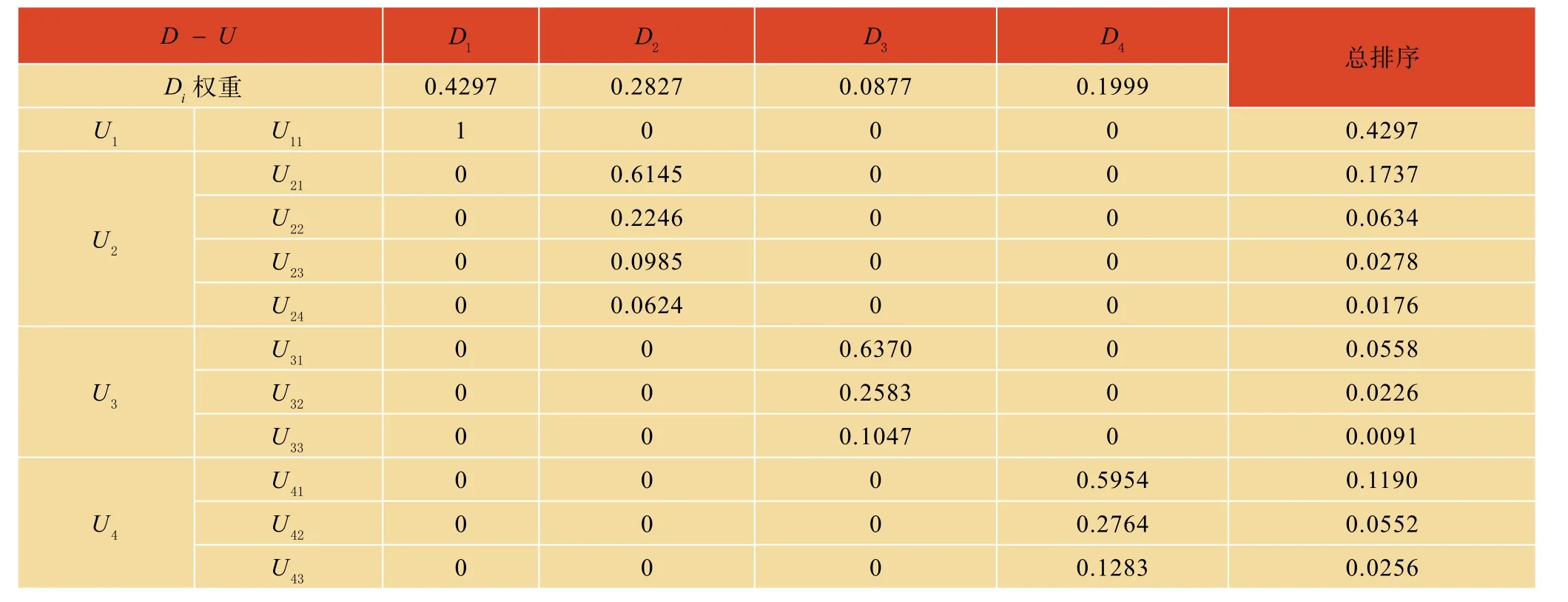
表4 总排序表Table 4 Total sort table

根据上述已经求出指标层中的各指标权重，在该工程项目评标众多指标因素中，工程报价中总造价是本工程项目中最大的权重因素，其次施工进度方案也是很重要的评标指标，其中施工前期准备工作作为评标主要考察因素。在评标过程中，应把这两个指标作为主要考察指标对投标单位进行评价。

3 基于层次分析法的模糊综合评价

3.1 模糊综合评价

计算结果得到每个投标单位的模糊综合评价值[15]。通过5位评委对各项二级指标的打分，得出综合模糊矩阵，并以A投标单位为例说明计算过程：

（1）二级模糊综合评价模型

用单因素评价计算，得到关于权重W的综合评判公式[16]：；据此得：

（2）一级模糊综合评价模型

其他两家计算过程类似，结果如表5所示：

表5 各单位模糊综合评价值表Table 5 Fuzzy comprehensive evaluation value table for each unit

3.2 确定投标单位的等级和排序

三家的最终分数排名如表6所示：

表6 投标单位得分表Table 6 Bid unit score table

通过综合评估各项评标标准，分别得出了建筑公司A、B、C三家的相对优劣情况。通过对表中的数据进行分析，可以得知：B公司的得分在三家公司里是最高的，A公司的投标方案仅次于B公司，依据最终的排序得出结论：B公司是最佳中标单位。

4 结论

本文运用层次分析法对工程评标实例进行建模，模糊综合评判后选出最佳投标单位。将原先定性的工程评标评审转化为定性和定量相结合的工程评标评审方式。通过对评标指标的权重排序，得出对投标单位评分的主要参考指标是总造价，其次是施工进度方案，评标过程中应着重考察这两个指标。再运用模糊综合评判对投标单位进行评分选出投标单位，使得评标方法更加完善、公平、科学地应用到实际工程项目中。

[1] 成龙. 基于AHP-TOPSIS的履带式全地形车总体性能指标体系评价分析[J]. 新型工业化, 2018, 8(2): 57-63.CHENG long. Evaluation and analysis of the overall performance index system of tracked ATV based on AHP-TOPSIS [J]. The Journal of New Industrialization, 2018, 8 (2): 57-63.

[2] 何芙蓉. 层次分析法在施工招投标中的应用研究[D]. 成都: 西南交通大学, 2014.HE Fu-rong. Application of analytic hierarchy process in construction bidding: [D]. Chengdu: Southwest Jiao Tong University, 2014.

[3] 韩黎明. 基于模糊层次的建设项目评标方法应用研究[D]. 天津: 河北工业大学, 2012.HAN Li-ming. Application of bid evaluation method based on fuzzy level in construction projects [D]. Tianjin: Hebei University of Technology, 2012.

[4] 王宏志, 朴东升. 多关系中基于层次的实体识别算法[J]. 新型工业化, 2012, 2(12): 56-68.WANG Hong-zhi, PU Dong-sheng. Multi level hierarchical entity recognition algorithm [J]. The Journal of New Industrialization, 2012, 2 (12): 56-68.

[5] 樊燕燕. 模糊综合评判法在建设工程评标中的应用[J]. 基建优化, 2003(4): 7-8.FAN Yan-yan. Application of fuzzy comprehensive evaluation method in bid evaluation of construction projects[J]. Optimization of Infrastructure Construction, 2003 (4): 7-8.

[6] 邹和礼, 赵暑生, 张龙祥. 基于定量与定性指标综合分析的工程项目评标方法[J]. 铁道学报, 2000, 22(6): 112-115.ZOU He-li, ZHAO Shu-sheng, ZHANG Long-xiang. Methods of bid evaluation for engineering projects based on comprehensive analysis of quantitative and qualitative indicators [J]. Journal of Railways, 2000, 22 (6): 112-115.

[7] 周剑, 陈杰.工业行业两化融合发展水平评估研究[J]. 新型工业化, 2011(1): 85-95.ZHOU Jian, CHEN Jie. Evaluation of development level of integration of two industries in industry [J]. The Journal of new industrialization,2011 (1): 85-95.

[8] 郑弦. 设计施工总承包招标评标指标体系研究[D]. 武汉: 武汉理工大学, 2013.ZHENG Xian. Design and construction of General Contracting Bidding Evaluation Index System [D]. Wuhan: Wuhan University of Technology, 2013.

[9] 孙铭忆. 层次分析法(AHP)与网络层次分析法(ANP)的比较[J]. 中外企业家, 2014(4): 67-68.SUN Ming-yi. Comparison between analytic hierarchy process (AHP) and network analytic hierarchy process (ANP)[J]. Chinese & Foreign Entrepreneurs, 2014(4): 67-68.

[10] 常建娥, 蒋太立. 层次分析法确定权重的研究[J]. 武汉理工大学学报(信息与管理工程版), 2007, 29(1):153-156.CHANG Jian-e, JIANG Tai-li. Analytic hierarchy process for determining weights[J]. Journal of Wuhan University of Technology(Information & Management Engineering), 2007, 29(1): 153-156.

[11] 梁礼明, 吴莉, 谢荣浩. 基于层次分析法的工程评标应用研究[J]. 江西理工大学学报, 2006, 27(1):61-63.LIANG Li-ming, WU Li, XIE Rong-hao. Application Research of project evaluation based on analytic hierarchy process [J]. Journal of Jiangxi University of Science and Technology, 2006, 27(1):61-63.

[12] 潘彬, 张得让. 政府采购招标项目评标方法—基于模糊数学综合评判分析法[J]. 系统工程, 2007, 25(2): 97-100.PAN Bin, ZHANG De-Lang. Bid evaluation method of government procurement bidding project based on fuzzy mathematics comprehensive evaluation and analysis method [J]. System Engineering, 2007, 25 (2): 97-100.

[13] 葛波. 基于层次分析法的工程项目评标应用研究[J]. 中国房地产业, 2011(5): 31.GE Bo. Application study of bid evaluation of engineering projects based on AHP [J]. Real Estate Information of China, 2011(5): 31.

[14] 杨学英. 层次分析法及模糊综合评判在工程评标中的应用[J]. 科技进步与对策, 2002(12): 132-133.YANG Xue-ying. Application of analytic hierarchy process and fuzzy comprehensive evaluation in project bid evaluation [J]. Progress and Countermeasures in Science and Technology, 2002 (12): 132-133.

[15] 林聚任, 刘玉安. 社会科学研究方法[M]. 济南: 山东人民出版社, 2004.LIN Ju-ren, Liu Yuan. Social science research method [M]. Jinan: Shandong people’s publishing house, 2004.