混合智能算法输电线路故障识别研究

刘武斌，彭华厦

（湖南工业大学，湖南 株洲 412008）

0 引言

输电线路是电力系统的重要组成环节，其功能是将电能从发电侧经升压/降压直至负荷侧，这是电厂与用户之间的联系。由于暴露在周遭环境当中，输电线路经常发生短路、雷击等事故。鉴于此，输电线路故障在全球范围内频繁发生并导致严重的电力事故。最常见也是最危险的输电线路故障是短路故障，分为相与相之间的短路和相与地之间的短路。单相接地短路是最常发生的短路形式，三相短路发生的概率则在各短路故障形式当中最低。

当系统发生短路故障时，故障相存在较大的短路电流，且电压会突然下降，近似为零。短路故障不仅产生热效应和机械效应，严重损坏电气设备，并且降低电能质量。更严重的后果是产生级联故障，危及电力系统的稳定性，从而导致整个系统的崩溃。因此，电力系统故障识别任务中，首要考虑输电线路短路故障的识别[1]。

选择和提取故障特征是故障分析的关键，最终选线的结果很大程度受特征向量选取的好坏程度所影响。目前，故障特征的提取方法已被许多国内外专家学者所研究。特征量一般可划为三大类：时频特征、时域特征和频域特征。而作为常用于提取故障信号的则是小波变换这一种时频特性方法。如利用这种方法提取电流的小波变换系数作为故障分析的特征向量。文献[2]用小波变换表示当前故障分量的瞬态能量，通过比较三相之间能量的差异来识别故障类型并区分故障。U.D.Dwivedi[3]等学者利用小波变换得到系数d1，计算出各相的系数变化值Δd，如果Δd比给定的阀值大，则每相计算各自的标准差，标准差再与阀值相比较，其中一相标准差若与阀值进行比较结果不同，偏大或偏小，则判定这一相为故障相，然而这种方法的缺点是人为设定阀值，不具一般性。在文献[4]中，同样通过小波变换提取故障电流瞬态信号的瞬态特性，以计算出来的分布权重作为判断依据。故障电流信号的特征向量同样在文献[5]中利用小波变换得到，进而利用模糊逻辑推理规则对传输线路的九个不对称故障进行分析。

特征量提取完成后，下一步就是对电力系统的故障类型进行识别。跟随技术发展的步伐，传统的神经网络越来越多地应用于电力网络的各个方面。其中，电力系统的故障识别和诊断也被囊括之中。例如，文献[6]使用小波能量熵提取故障特征向量，然后输入基于最小二乘支持向量机的故障相位选择方法进行故障分类，提出了一种小波能量熵与支持向量机相结合的相位选择方法，具有很高的可靠性。文献[7]中提出基于BP神经网络和小波变换的输电线路故障选相方法，通过分析在各种情况下小波能谱熵在不同尺度下的分布情况，构造BP神经网络进行故障选相，准确率比较高，可以处理系统复杂的信息，但具有小波能量熵计算量大、网络输入维数较多、网络训练速度慢、构建训练样本工作量较大等不足。文献[8]提出了一种故障分类系统，该系统配合使用蚁群算法与模糊神经网络两大人工智能算法处理配电网故障。

现实当中的输电线路短路故障存在着检测的误差，即噪声污染，如设备自身存在着检测误差，产生的噪声数据将影响系统的故障识别准确率，虽然噪声在海量数据当中微乎其微，但是对于输电线路这一特殊的系统，一次误判就足以带来严重的后果。在完成降噪之后进行的输电线路短路故障识别研究在国内外当中仍然较少，则文章利用DBSCAN（Density-Based Spatial Clustering of Applications with Noise）聚类算法对特征量数据进行降噪之后，再作为PNN神经网络的训练和测试数据进行分类，而神经网络自身的分度密度SPREAD参数也利用了准确率作为GA中的适应度函数值进行了优化，从而提高分类的准确率。最后在MATLAB软件平台上进行了算例的分析，从而验证了算法的可行性和有效性。

1 DBSCAN聚类算法

DBSCAN[9]是一种基于密度的聚类算法。在DBSCAN算法中，每个聚类中都有一个典型的点密度，这个密度远高于聚类外。而且，噪声区域内的密度低于任何群集中的密度[10]。利用DBSCAN算法的这一可以挖掘任何形状的簇的特点，则能够排除数据群中的噪声节点。定义半径ε为对象p为对象集）的 ε 邻域，实质上 ε 的值限制了核心点在空间中的搜索范围。密度阈值Minpts为使对象p成为核心点的密度限定值。若对象p的ε邻域内对象个数n大于密度阈值Minpts，则定义p为核心点。对于给定对象集的ε邻域，则称q从p直接密度可达。若p1=p，pn=q，从pi+1关于ε和Minpts直接密度可达，则对象q是从对象p关于ε和Minpts密度可达。若∀ο∈D，使得对象p和q密度可达，那么对象p和是q密度互连的。当然，若对象p不属于任何簇，则p为噪声。

[引理 1]对于给定的Minpts和ε，p是数据集合中的一个对象，并且，那么一个集合与 p 密 度连接}就是一个聚类。

簇C中的每个对象都连接到任意核心对象密度。相反，C中包含的对象也是那些连接到C中的任何核心对象密度的对象。

[引理 2]对于给定的Minpts和ε，C是一个聚类，p是集合C中的一个对象并且，那么C就等同于一个集合:从p 可以密度可达ο}。

如图1所示，设ε领域内 Minpts= 3，则有：

1）所标记的点M、P、O和R都是核心点；

2）M从P可“直接密度可达”，而Q则从M可“直接密度可达”；

3）Q从P“密度可达”，但P从Q不能“密度可达”（非对称）；S和R从O“密度可达”；

4）O、R和S均“密度互连”的。

图1 区域查询Fig.1 Area query

如图2所示DBSCAN 聚类算法对输电线路采集的电压电流特征量的聚类结果，其数据来源于长株潭城际轨道交通牵引变电所所采集的铁路输电线路电压电流标幺值，并已提取特征向量。为了对短路故障分类的目的，数据增加了短路的电压电流特征量而相对应的减少了稳定运行的特征量，并在神经网络训练之前归一化。由图可知DBSCAN 聚类算法很好地将噪声（设备的检测误差数据）标记了出来（红点）。

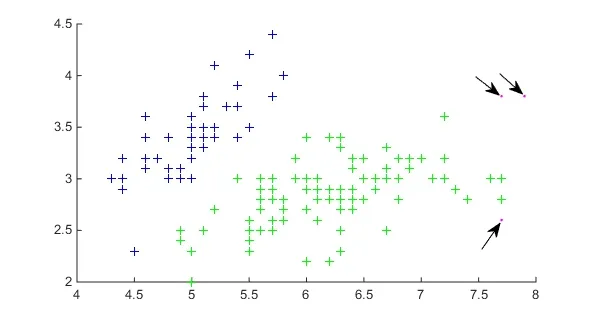
图2 DBSCAN聚类结果Fig.2 DBSCAN clustering results

2 PNN神经网络

概率神经网络（probabilistic neural networks, PNN）[11]是通过用指数函数代替神经网络中经常使用的S形激活函数，形成可以计算接近贝叶斯最优的非线性决策边界的神经网络。一般四层神经网络就可以将任何输入模式映射到任意数量的分类。决策边界可以在新数据可用时实时修改，并且可以使用完全并行操作的人造硬件“神经元”来实现[12]。PNN是一种由竞争层和径向基层组成的监督学习网络[13]。作为径向基神经网络，PNN为反向传播的增量自适应时间占总计算时间很大一部分的问题提供了巨大的速度优势，模式识别和分类能力优于BP网络。其结果始终收敛于稳定性较好的贝叶斯最优解，而且它具有一定的抗噪声性能，可包容含有某些错误的样品[14]。与其他神经网络拓扑相比，PNN通过选择适当的平滑参数值，决策表面的形状可以根据需要制作得复杂或简单，适合于实时硏究故障诊断巧信号分类问题的研究。

当分布密度SPREAD的近似等于0时，它构成最近邻分类器；当SPREAD的值趋于无求大时，它构成了几个训练样本的相邻分类器[15]。PNN网络一般由四个结构层组成：输入层、样本层、累加层和输出层，其基本结构如图3所示。输入样本向量的个数与样本层神经元个数相等，样本数据的种类数则与输出层神经元个数相等，输入层节点的数量是样本向量的维数。在将所有样本恒量地传递到样本层之后，输入向量的每个子向量在样本层执行加权求和，然后使用非线性算子执行计算，计算结果被传递到累积层。通常，非线性算子采用高斯函数：

式中，iW为输入层到模式层连接的权值，σ为平滑因子。

图3 PNN基本结构Fig.3 Basic structure of PNN

根据方程（1）计算出求和层，它属于某一类的累积概率，以及失效模式的估计概率密度函数（Probability Density Function, PDF）。每个类别对应一个求和层单位，求和层单位连接属各自类别的模式层单位，即求和层单元只将属于各自类别的模式层单元输出相加。各类别的概率密度的基于内核的估计与求和层单元的输出成比例。通过输出层的归一化数据处理，可以获得各种类别的概率估计值。作为一种竞争神经元的输出层由一个阀值识别器组成，其作用是将其中一个具有最大后验概率密度的神经元从每个失效模式当中筛选出作为整个系统的输出。每个神经元对应一种数据类别，即短路故障模式。训练样本数据量与输出层神经元的个数相等，求和层各种类型的输出则从输出层的各神经元输出。待识别的样本模式类别的概率密度函数和为1，相应地其他神经元的输出全部为零。

利用PNN来对故障进行诊断的方法被广泛认为是概率统计中的一种决策方法。这种方法可以被叙述为：假设有两种已知的故障模式并且为故障特征样本：

若，则

若则

式中， N为训练样本总数； NA、 NB则分别为故障模式δA、δB的训练样本数；uA、uB为故障模式 δA、 δB的先验概率；vA为将样本属于 δA的故障特征样本X错误地划分到模式δB的代价因子；同理定义错判代价因子vB。PA、PB为故障模式δA、δB的PDF，通常并不能计算出PDF的精确值，只能利用现有的样本计算其统计值。

Parzen窗口概率密度估计方法在1962年被Parzen所提出。只要足够的学习训练样本得到保证，就可以确保网络收敛到任何复杂程度的未知密度。这种方法不需要提前设定任何学习训练的样本的分布。由Parzen方法得到的PDF估计式如下：

式中，d为样本向量的变量个数；σ为平滑参数，其取值确定了以样本点为中心的钟状曲线的宽度；Xai为故障模式δA的第i个训练向量；m为故障模式δA的训练样本数目。

3 算例分析

在PNN网络模型中，利用GA不受函数连续与可微的限制，并且全局可优的优势，运用GA对PNN的分度密度SPREAD参数值进行优化，寻找最优参数。GA步骤如下：

1）设定SPREAD值的取值范围，随机初始种群，n为种群规模，并设t=1；

2）根据染色体获得的SPREAD值，构建PNN网络，计算分类正确的数目及存在的误差，即计算染色体的适应度函数；

3）选择优胜的个体，进行交叉、变异操作，得到下一代种群；

4）设当前代数 t=t+ 1；

5）若当前迭代次数达到预先设置的迭代次数（或达到最小误差要求），则迭代停止，输出最优解，否则转到步骤②；

6）利用优化后得到的SPREAD值确定PNN网络模型。

图4给出了PNN网络的总体设计流程，表1给出了各故障类型标签及数据分布情况。总计110个数据，100个作为训练集，10个作为测试集。

表1 各故障类型设置Table 1 Fault Type Settings

如图5、6所示，在没有优化SPREAD值之前，SPREAD值取1.5，PNN网络训练的结果很差，有5个样本判断错误，在用预测样本进行验证的时候，仍有一个样本即输电线路短路故障类型判断错误。在GA优化（如图7 GA优化过程）后的PNN网络准确率大幅度提升，如图8、9所示，训练样本只有一个判断错误，预测样本达到了百分之百准确。

图4 PNN网络设计流程图Fig.4 Design flow chart of PNN

图5 未优化训练效果及误差Fig.5 Unoptimized training effects and errors

图6 未优化预测效果Fig.6 Unoptimized predictions

图7 GA优化过程Fig.7 GA optimization process

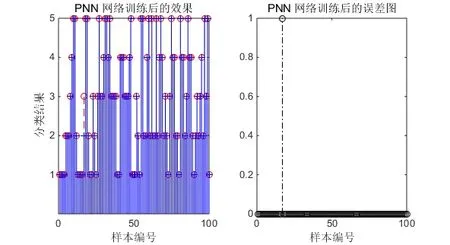
图8 优化后训练效果及误差Fig.8 Optimized training effects and errors

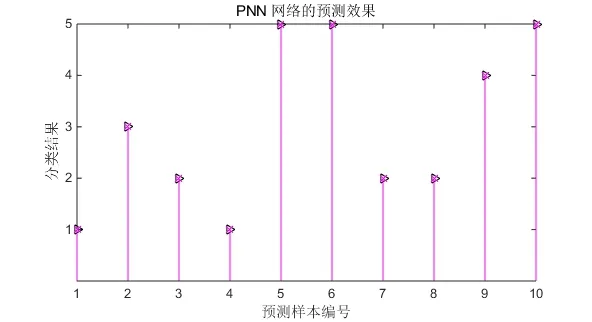
图9 优化后预测效果Fig.9 Optimized predictions

4 结论

输电线路是电力系统各环节的重要纽带，而又是发生故障的频繁区域，对输电线路短路故障的识别则变得尤为重要。文章将PNN网络与聚类算法相结合，利用DBSCAN聚类算法将噪声移除，使将要训练的数据较少地影响PNN网络对输电线路短路故障类型分类的准确率。与此同时，文章亦应用了GA算法对PNN网络的分度密度SPREAD参数进行了优化，使准确率进一步提升。最后通过MATLAB仿真软件对算例的模拟实验验证了该故障诊断识别方法的可行性和有效性。

[1] 马丹丹. 输电线路故障暂态信号分析和行波测距研究[D]. 成都: 西南交通大学, 2008.MA Dang-dang. The study on traveling wave fault location and analysis of fault transient signal in transmission line[D]. Chengdu: Southwest Jiaotong University, 2008.

[2] 段建东, 张保会, 周艺, 等. 基于暂态量的超高压输电线路故障选相[J]. 中国电机工程学报, 2006, 26(3): 1-6.DUAN Jian-dong, ZHANG Bao-hui, ZHOU Yi, et al. Transient-based faulty phase selection in EHV transmission lines[J]. Proceedings of the CSEE, 2006, 26(3): 1-6.

[3] DWIVEDI U D, SINGH S N, SRIVASTAVA S C. A wavelet based approach for classification and location of faults in distribution systems[C]//India Conference, 2008. INDICON 2008. Annual IEEE. IEEE, 2008, 2: 488-493.

[4] 何正友, 陈小勤, 罗国敏, 等. 基于暂态电流小波熵权的输电线路故障选相方法[J]. 电力系统自动化, 2006, 30(21): 39-43.HE Zheng-you, CHEN Xiao-qin, LUO Guo-min , et al. Faulted phase selecting method of transmission lines based on wavelet entropy weight of transient current[J]. Automation of Electric Power Systems, 2006, 30(21): 39-43.

[5] YOUSSEF O A S. Combined fuzzy-logic wavelet-based fault classification technique for power system relaying[J]. IEEE transactions on power delivery, 2004, 19(2): 582-589.

[6] 张明光, 陆文辉, 刘昱晨. 基于小波能量熵和支持向量机的高压输电线路故障选相方法研究[J]. 电气自动化, 2011, 33(6): 67-70.ZHANG Ming-guang, LU Wen-hui, LIU Yu-chen. Research on a new faulty phase selector of high voltage power transmission lines based on wavelet energy entropy and SVM[J]. Electrical Automation, 2011, 33(6): 67-70.

[7] 燕洁, 杨淑英. 小波变换和 BP 网络在输电线路故障类型识别中的应用[J]. 东北电力技术, 2007(7): 43-45.YAN Jie, YANG Shu-ying. On Wavelet Transform and the Application of BP Network to the Fault Identification of Power Transmission Line[J]. Northeast Electric Power Technology, 2007(7): 43-45.

[8] 孙鹏, 曹雨晨, 刘洋, 等. 采用二进制蚁群模糊神经网络的配电网故障分类方法[J]. 高电压技术, 2016, 42(7): 2063-2072.SUN Peng, CAO Yu-chen, LIU Yang, et al. Fault classification technique for power distribution network using binary ant colony algorithm and fuzzy neural network[J]. High Voltage Engineering, 2016, 42(7): 2063-2072.

[9] ESTER M, KRIEGEL H P, SANDER J, et al. A density based algorithm for discovering clusters in large spatial database with noise[C]//Proc 2nd Inter Conf Know Discove Data Mining. Portland: AAAI Press, 1996: 226-231.

[10] 韩家炜, 米歇林·坎伯, 裴健. 数据挖掘概念与技术[M]. 范明, 孟小峰, 译. 北京: 机械工业出版社, 2012.HAN J W, KAMBER M, PEI J. Data Mining: Concepts and Techniques[M]. FAN M, MENG X F, Trans. Beijing: Machinery Industry Press, 2012.

[11] SPECHT D F. Probabilistic Neural Networks. Neural Networks, 3:109-118[J]. 1990, 3(1):109-118.

[12] MISHRA S, BHENDE C N, PANIGRAHI B K. Detection and Classification of Power Quality Disturbances Using S-Transform and Probabilistic Neural Network[J]. IEEE Transactions on Power Delivery, 2007, 23(1): 280-287.

[13] ALI J B, SAIDI L, MOUELHI A, et al. Linear feature selection and classification using PNN and SFAM neural networks for a nearly online diagnosis of bearing naturally progressing degradations[J]. Engineering Applications of Artificial Intelligence, 2015, 42(C): 67-81.

[14] SPECHT D F, SHAPIRO P D. Generalization accuracy of probabilistic neural networks compared with backpropagation networks[J]. Journal of Vector Ecology, 2011, 36(2):426-36.

[15] KUSY M, ZAJDEL R. Application of reinforcement learning algorithms for the adaptive computation of the smoothing parameter for probabilistic neural network[J]. IEEE transactions on neural networks and learning systems, 2015, 26(9): 2163-2175.

[16] 夏飞, 罗志疆, 张浩, 等. 混合神经网络在变压器故障诊断中的应用[J]. 电子测量与仪器学报, 2017, 31(1):118-124.XIA Fei, LUO Zhi-jiang, ZHANG Hao, et al. Application of mixed neural network in transformer fault diagnosis[J]. Journal of Electronic Measurement and Instrument, 2017, 31(1):118-124.

[17] 陈少锋, 黄玉龙. 一种考虑电机间振动影响的电机轴承故障诊断方法[J]. 新型工业化, 2017, 7(10): 69-76.CHEN Shao-feng, HUANG Yu-long. A Motor Bearing Fault Diagnosis Method Considering the Vibration Interaction between Motors [J]. The Journal of New Industrialization, 2017, 7(10): 69-76.

[18] 刘方园, 王水花, 张煜东. 卷积神经网络架构及其应用的研究[J]. 新型工业化, 2017,7(11): 40-51.LIU Fang-yuan, WANG Shui-hua, ZHANG Yu-dong. Research on Architectures and Applications of Convolutional Neural Network [J]. The Journal of New Industrialization, 2017,7(11): 40-51.

[19] 肖晓, 徐启华. 基于SVM与BP的分类与回归比较研究[J]. 新型工业化, 2014(5):48-53.XIAO Xiao, XU Qi-hua. A Comparative Research on the Classification and Regression Based on SVM and BP [J]. The Journal of New Industrialization, 2014(5):48-53.

[20] 徐步云, 倪禾. 自组织神经网络和K-means聚类算法的比较分析[J]. 新型工业化, 2014(7):63-69.XU Bu-yun, NI He. Comparative analysis of SOM and K-means clustering [J]. The Journal of New Industrialization, 2014(7):63-69.