基于分层前推回代法的配电网潮流计算研究

张丽虹

（贵州大学电气工程学院，贵州 贵阳 550025）

0 引言

配电网电力系统与输电网相比具有两个主要特点：一是大多数配电网都是辐射状或少环结构的，二是配电线路R/X 较大，且线路的充电电容可以忽略。而对于配电网电力系统而言，除了上述配电网两点之外还具备两个特点：一是其配电线路较短，阻抗很小，而且由于电气距离短，相间的耦合严重；二是负荷分布不对称，进而造成系统运行具有很大的不对称性[1-4]。

潮流计算是电力系统暂态稳定计算和静态稳定计算的基础，也是电力系统暂稳态分析的重要工具[5]。配电网潮流分析是配电网分析的基础, 配电网的网络重构、故障处理、无功优化和状态估计等都需要用到配网潮流的数据[6-8]。目前，配网潮流分析方法主要分为母线法和支路法两大类，支路法又可分为回路法、前推回代法、牛顿拉夫逊法、高斯塞德尔法和快速解耦法[9-10]。

根据配电网电力系统负载功率大，输电线路短的特点，传统的高斯—塞德尔法、牛顿—拉夫逊法、快速解耦法等均不再适用[11-12]。目前在配电网电力系统中普遍采用的是前推回代的潮流计算方法[13]。本文基于该方法，提出分层的前推回代法，不仅在计算速度上有了很大的提高，而且可应用于多节点、多支路的并行计算中。

1 分层的前推回代法

在传统的配电网前推回代潮流计算方法的基础上，首先将电力系统中的所有电气节点、支路进行分层，最上层为根节点，下层节点以二叉树的形式布置，节点和支路按照从上至下，从左至右的原则进行编号。其基本原理是令根节点为三相电压幅值和相角已知的平衡节点，初始化时令其他所有节点电压等于此根节点电压。

“前推”过程是从最底层的叶节点开始，先计算此节点上负载的注入电流，然后根据网络中各支路的性质和支路两端节点电压可以求出支路的首端电流。“回代”过程是从根节点出发，通过“前推”过程计算出的各支路电流值[3]，依次确定各支路的电压损耗，从而按层次关系更新各节点的电压值，直到计算到最底层的节点。

回代计算各支路电流：对于馈线段支路L，其末端电流为：

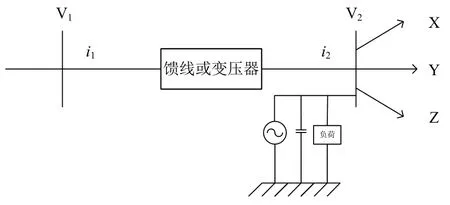
图1 分层前推回代法的数学模型Fig.1 Mathematical model of layered forward and backward substitution method

其始端电流为：

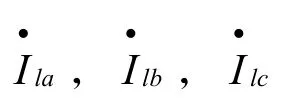
对于变压器支路，支路L的末端电流为：

将（4）的计算结果代入下式，可得变压器支路L的始端电流：

前推求节点电压：从第一层根节点开始向最后一层的叶节点推进。对于馈线段支路，节点j的电压为：

对于变压器支路，节点j的电压为：

迭代收敛的判据：

如果（7）式中电压不平衡量中任何一个大于收敛判据，则重复以上步骤直至收敛。

PV节点的处理：当按给定的端电压进行发电时，在计算过程中需要保持节点的电压恒定，此时需要将PV节点转化为PQ节点[14]，为了既可保持前推回推潮流计算的高效性，又能有效处理PV节点，采用在PV节点叠加补偿电流的方法。设系统有m个PV节点，当进行到第k次迭代时：

（1）电压幅值的不平衡量

为给定的PV节点j的三相电压幅值。

（2）无功注入补偿电流

PV节点j的无功注入补偿电流增量为：

PV节点j的无功注入补偿电流为：

因为发电机的无功输出有一定的范围，必须首先检查无功注入是否越限。

PV节点需要注入的无功功率为：

需要满足计算的无功功率在发电机的无功限值范围之内，即：

若满足条件（13），则可将无功补偿电流在随后的迭代中叠加到相应的节点上。否则，注入无功功率设定为发电机的限值，PV节点转化为PQ节点。

这种特点一方面限制了不同层次间的电流前推和电压回代不能同时进行，另一方面同一层次的支路电流之间没有前后关联，完全可以实现电流或电压的并行计算，尤其对于大规模辐射状网络，由于分层数显著小于支路数，所以分层后能够充分发挥并行计算的优势，提高计算速度[15-16]。

2 潮流计算程序

主程序首先进行初始化，并通过调用“参数设置”子程序读入系统网络结构参数。本程序中，除PV节点外，假定其他节点的电压和相角的初始值均与根节点一致，并以从节点流出的方向为电流的正方向。对于PV节点，其输出有功功率和电压均为已知。但是，程序中处理PV节点时，将其当成PQ节点，并辅以注入无功功率修正值的方法来保证PV节点的电压不变。因此，在初始化过程中，必须给PV节点的无功功率给定一个初值。经过验证，该值可以为任意值，为了方便，程序中将所有PV节点的无功功率初值设定为0。

然后从最远一层开始循环，逐个求各节点和各支路的电流值，各节点的注入电流值和该节点上所连接的负荷、电容器和电动机的个数有关，支路电流由该支路的类型所决定（输电线或变压器），前推到根节点后进行回推更新除了PV节点外的所有节点的电压值，并判断结果是否收敛，收敛的条件是第k次和第k-1次的节点电压值的差是否小于给定的收敛系数，若收敛则退出迭代循环程序输出结果，否则继续循环直到收敛，当循环次数达到一定值（如50次）仍未收敛时，则程序会人为的被终止。

图2 潮流计算程序流程图Fig.2 Power flow calculation program flow chart

3 算例分析

本文分别选取辐射状8节点网络系统和IEEE13节点标准测试系统进行分析。对于一8节点的多层多分支网络结构，采用恒功率负荷，已知系统参数有：节点电压10.5 kV；支路1阻抗0.54+0.65j Ω，支路2阻抗0.9+0.5j Ω，支路3阻抗0.72+0.75j Ω，支路4阻抗0.62+0.5j Ω，支路5阻抗0.65+0.35j Ω，支路6阻抗1.0+0.55j Ω，支路7阻抗0.6+0.35j Ω；节点2负荷0.6+0.45j mVA，节点3负荷0.5+0.4j mVA，节点4负荷0.6＋0.4j mVA，节点5负荷0.4+0.3j mVA，节点6负荷0.5+0.35j mVA，节点7负荷0.4+0.3j mVA，节点8负荷0.4+0.28j mVA。

基于分层理论，可将该系统按节点和负荷分成三层，再利用前推回代的潮流计算程序进行计算，其计算结果如下表所示：

表1 简单辐射状网络恒功率负荷算例潮流结果Table 1 Results of power flow of simple radial power network under the condition of constant power load

通过求解以上8节点辐射状网络算例，并与EMTDC结果比较可知，本潮流分析计算程序在分层计算上是正确的。

图3 8节点辐射状供电网Fig.3 Radial power network of 8 node

图4 IEEE13节点测试系统分层结构图Fig.4 Layered structure of IEEE13 test system

对于IEEE13节点标准测试系统，其分层结构图如图4所示：

已知根节点电压为2.4（标幺值），各支路参数和节点负荷参数都在表2中列出，节点5和节点8之间变压器支路。

IEEE所提供的13节点算例中，节点2与节点7之间存在分布式负荷，本文将分布式负荷近似为一个等价集中负荷，在节点2与节点7的支路中点，追加了一个节点4，并将该等价集中负荷接在节点

4上，故系统共有14个节点。通过以上验证可知，无论13节点还是37节点算例的验证中，本文潮流分析程序所计算结果与IEEE所提供的参考结果还是存在较大的差异。为了进一步验证程序的正确性，通过EMTDC对算例取部分节点进行验证，我们的结果与之更为接近，进而说明了本文所编写潮流分析计算程序的正确性。

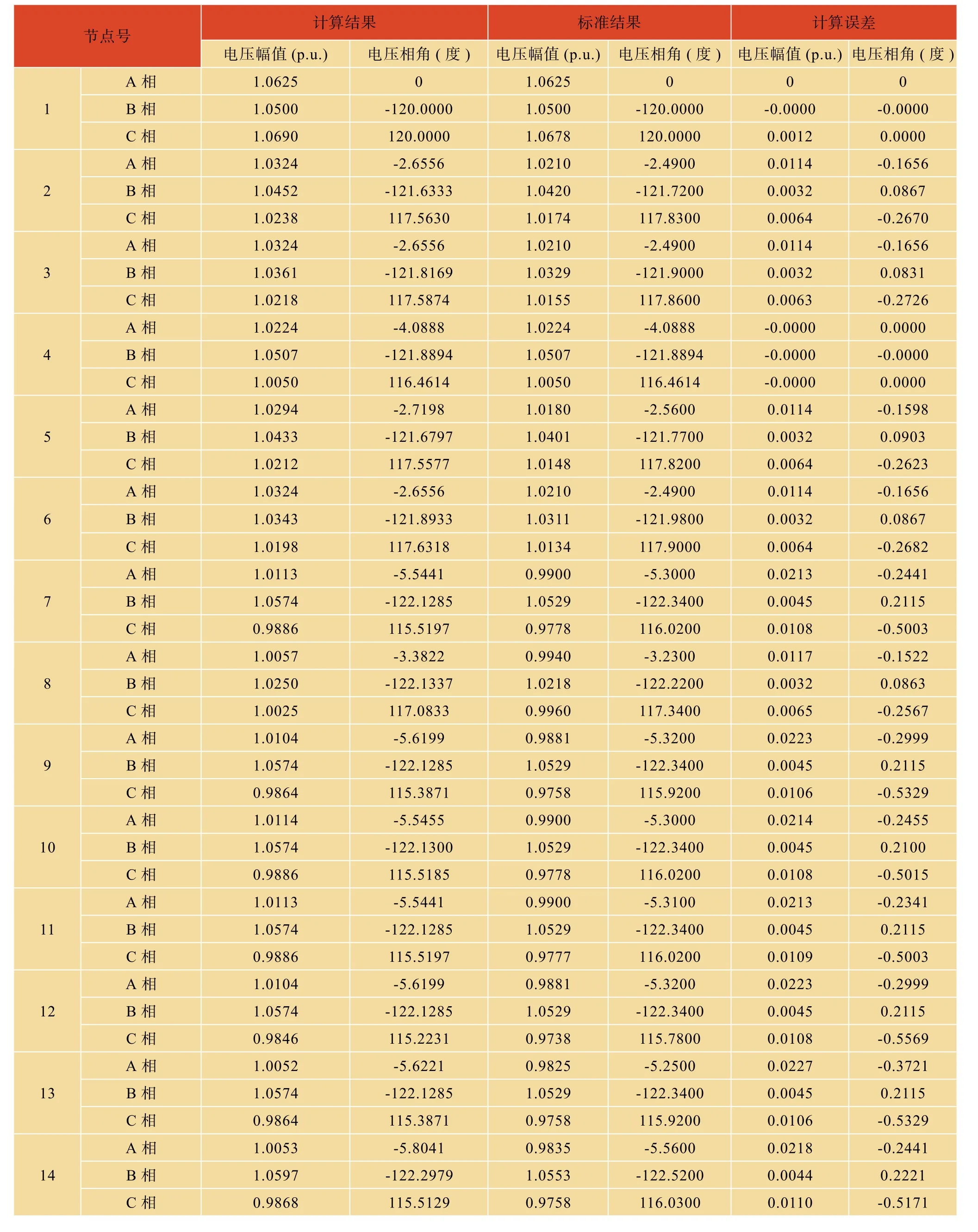
表2 13节点算例潮流分析结果Table 2 Results of power plow analysis of IEEE13 test system

4 结论

本文在传统的配电网前推回代潮流计算方法的基础上引入了分层的思想，将电力系统中所有支路和节点进行分层，再分别从叶节点和根节点开始进行前推和回代运算。这种算法不但能够充分利用并行计算的优势，而且能够显著提高计算的速度。通过算例验证，该平台能够较为准确的对配电网潮流进行运算，并且与EMTDC相比，得出的结果更接近于实际值。

[1] 吴耀东, 梁海峰, 高亚静, 等. 基于潮流追踪算法的自适应低频减载策略研究[J]. 中国电力, 2015, 48(3): 61-66.WU Yao-dong, LIANG Hai-feng, GAO Ya-jing, et al. Research on adaptive low frequency load shedding strategy based on power flow tracing algorithm [J]. Electric Power, 2015, 48 (3): 61-66.

[2] 刘路, 徐学勇, 陈俊长. 基于前推回代法的弱环配电网三相潮流计算[J]. 电气应用, 2014, 33(11): 36-39.LIU Lu, XU Xue-yong, CHEN Jun-Chang. Three-phase power flow calculation of weak loop distribution network based on forward backward substitution method [J]. Electrical Application, 2014, 33 (11): 36-39.

[3] 王雅倩. 基于前推回代法的含分布式电源的配电网潮流计算[J]. 贵州电力技术, 2015, 18(1): 86-90.WANG Ya-qian. Power flow calculation of distribution network with distributed generation based on forward backward substitution method [J].Guizhou Electric Power Technology, 2015, 18 (1): 86-90.

[4] 康文左, 张程柯. 基于潮流追踪的改进切负荷方法[J]. 电力系统及其自动化学报, 2015, 27(8): 97-102.KANG Wen-Zuo, ZHANG Cheng-ke. An improved load shedding method based on power flow tracing [J]. Journal of Power Systems and Automation, 2015, 27 (8): 97-102.

[5] CHEN X, HE J H, HE Y C. Analysis and management strategies for the low voltage problems of rural power grid based on the distribution network flow calculation method [J]. Journal of Chongqing University(English Edition), 2015, 14(4): 134-140.

[6] 谢秦, 刘冬梅. 含有分布式电源（光伏）的配电网若干问题研究[J]. 新型工业化, 2014, 4(8): 22-29.XIE Qin, LIU Dong-mei. Research on Several Problems of Distribution Network with Solar Power[J]. The Journal of New Industrialization,2014, 4(8): 22-29.

[7] 俞俊霞, 赵波. 基于改进粒子群算法的最优潮流计算[J]. 电力系统及其自动化学报, 2005, 17(4): 83-88.YU Jun-xia, ZHAO Bo. Optimal power flow calculation based on Improved Particle Swarm Optimization [J]. Journal of Power Systems and Automation, 2005, 17 (4): 83-88.

[8] 谢梦琼, 张学毅, 杨洋. 基于一种改进量子粒子群算法的配电网重构[J]. 新型工业化, 2017, 7(8): 37-41.XIE Meng-qiong, ZHANG Xue-yi, YANG Yang, et al. Distribution Network Reconstruction Based on Improved Quantum Particle Swarm Optimization [J]. The Journal of New Industrialization, 2017, 7(8): 37-41.

[9] WU H B, CAI L. A new approach combing connection number and fuzzy simulation to calculating power flow of distribution network considering uncertainty[J]. International Journal of Electrical Power & Energy Systems, 2013, 53(4): 884-892.

[10] 王震东, 刘白杨, 张随涵. 基于Matlab的牛顿-拉夫逊法电力系统潮流计算[J]. 电工电气, 2016(7): 61-62.WANG Zhen-dong, LIU Bai-yang, ZHANG Sui-han. Power flow calculation of power system based on Newton Raphson method based on Matlab [J]. Electrical and Electrical, 2016 (7): 61-62.

[11] 任雨柔. 基于Matlab的电力系统快速解耦法潮流计算研究[J]. 科技创新导报, 2016, 13(15): 82-84.REN Yu-rou. Research on power system fast decoupling power flow calculation based on Matlab [J]. Innovation Guide, 2016, 13 (15): 82-84.

[12] 彭穗, 何朋亮, 刘志伟, 等. 基于前推回代法和牛顿拉夫逊法的配电网潮流计算[J]. 电子测试, 2015(2): 52-53, 28.PENG Sui, HE Peng-liang, LIU Zhi-wei, et al. Power flow calculation of distribution network based on forward backward substitution method and Newton Ralph Xun Fa method[J]. Electronic Test, 2015 (2): 52-53, 28.

[13] 李欣然, 李龙桂, 童莹, 等. 适用于多电源配电网潮流计算的前推回代方法[J]. 电力系统及其自动化学报, 2017, 29(12): 121-125.LI Xin-ran, LI Long-gui, TONG Ying, et al. Forward backward substitution method for power flow calculation of multi power distribution network [J]. Journal of Power System and Automation, 2017, 29 (12): 121-125.

[14] 朱剑锋, 陈立东, 刘磊. 基于MATLAB 三相方波逆变电路仿真分析[J]. 新型工业化, 2017, 7(2): 72-76.ZHU Jian-feng, CHEN Li-dong, LIU Lei. Simulation and analysis of three phase square wave inverter based on MATLAB[J]. The Journal of New Industrialization, 2017, 7(2): 72-76.

[15] 严太山, 崔杜武, 陶永芹. 基于改进遗传算法的配电网故障定位[J]. 高电压技术, 2009, 35(2): 255-259.YAN Tai-shan, CUI Du-wu, TAO Yong-qin. Fault location of distribution network based on Improved Genetic Algorithm[J]. High Voltage Technology, 2009, 35 (2): 255-259.

[16] JALILI-MARANDI V, DINAVAHI V. SIMD-based large scale transient stability simulation on the graphics processing unit[J]. IEEE Trans on Power Systems, 2010, 25(3): 1589-1599.