异步电机基于SVPWM死区补偿控制方法研究

王文韬，郭维，甘韦韦，黄浩，王永通

（株洲中车时代电气股份有限公司，湖南 株洲 412001 ）

0 引言

空间矢量脉宽调制(space vector pwm, SVPWM)技术由于其输出电压电流谐波低且直流电压利用率高等优点而成为了交流传动领域研究的热点[1-2]。在异步电机矢量控制系统中，为了防止逆变器同一桥臂发生直流导通，一般会加入死区时间，但死区时间的存在将使逆变器的实际输出电压电流波形产生畸变，引发转矩脉动，甚至导致系统不稳定[3-5]。因此，许多学者对死区补偿展开了深入的研究，并提出了多种补偿方法。这些方法可以归纳为两种：一种是硬件补偿法，这种补偿方式存在补偿滞后的问题，同时又要增加成本，增加了系统的复杂性。另一种是软件补偿法，通过在电机控制程序中加入死区补偿的算法来进行补偿，这种方法不需要额外添加硬件，简单灵活。比较典型的有电流反馈补偿法，然而，电流反馈补偿法大多需要对电流极性进行检测,这些方法会受到电流噪声、直接滤波所带来的相位滞后等问题的影响,而使补偿效果不理想,尤其在低频、轻载的情况下,这种问题更加明显。因此,寻求一种简单而有效的死区补偿方法至关重要。

本文通过对逆变器死区效应产生的原因及影响深入分析，并综合电流反馈法和平均电压补偿法，总结出了一种死区补偿方法，也称之为坐标变换电流反馈法，该方法很好地解决了由于电流噪声所带来的电流过零点检测困难，以及对电流直接滤波会产生相移这两个问题。其原理为：三相静止坐标系A-B-C下的电流在d-q轴下表现为直流量，对它进行滤波就不会使其幅值和相位发生变化，再将它从d-q坐标系变换至A-B-C三相坐标系，进行电流极性检测，就可以避免电流检测中出现多个零点的现象，同时也避免了直接对电流滤波后进行检测带来的相位滞后影响，通过仿真实验证明，该补偿方法能得到很好的补偿效果，有一定的工程应用值。

1 SVPWM逆变器死区效应分析

为了防止逆变器同一桥臂发生直流导通，需要加入死区时间，在死区时间内同一桥臂的上、下开关器件都处于关断状态，此时该相的输出电压处于失控状态，其值决定于该时刻输出电流的方向，虽然死区时间很短，单个脉冲不会影响系统的性能，但连续死区效应的积累会使电动机的定子电压电流产生畸变，特别是在低速轻载时，死区效应的影响将会导致逆变器输出电流发生畸变，从而引发转矩脉动，甚至可能会引起系统发生振荡。

以A相桥臂为例分析死区时间对电压源逆变器所产生的影响，假设功率开关器件为高有效触发（忽略开通关断时间），图1（a）和（b）分别为(ia＞ 0)和(ia＜ 0)时A相桥臂的电流流向。

图1 逆变器A相桥臂电流流向Fig.1 Inverter phase a bridge current flow

（ ia＞ 0）时，根据图1(a)和图2(a)～(e)分析一个PWM周期（ t1−t5）中，死区对输出电压的影响。当t=t1时，VT1关断，VT2并没有马上开通，而是延时Td再开通，则在（ t1−t2）时间段里，电流通过D2续流，输出电压为零，当 t=t2时，VT2开通，输出电压继续为零，当 t=t3时，VT2关断，VT1延时Td再开通，在这段时间 t3−t4里，电流通过D2续流，输出电压为零，当 t=t4时，VT1开通，输出电压为Udc,当 t=t5时，VT1关断，输出电压为零，整个输出电压波形如图2(c)所示。

同理可以对(ia＜ 0)的情况加以分析，这里就不再赘述。

通过分析可知，在一个PWM周期里，当电流为正时(ia＞ 0)，输出电压正脉冲变窄，输出电压值比期望值低, 死区的影响相当于损失了一个方波电压如图2(c)中的阴影部分Uwu所示，亦可看做在一个PWM周期里，它产生了一个与原电压方向相反的误差方波电压如图2(d)所示；当电流为负时( ia＜ 0)，输出电压负脉冲变窄，输出电压值比期望值高。误差电压以脉冲的形式出现，与电流极性方向相反，一般死区时间设置为微秒级，单个脉冲不会影响系统的性能，但持续积累就会使输出电流波形产生畸变，引发转矩脉动。

图2 逆变器的触发脉冲及输出电压（ ia＞ 0，死区时间为Td）Fig.2 Inverter trigger pulse and output voltage ( ia＞ 0, dead time Td)

2 坐标变换电流反馈死区补偿的原理及实现

（1）坐标变换电流反馈死区补偿的原理

坐标变换电流反馈法的原理为：通过检测逆变器的三相输出电流，得到误差方波电压经过相应的折算后叠加到SVPWM调制方式的输出波形中，这个方波信号使逆变器产生一个与电流同相位的补偿电压。此方法的实质是把误差电压平均补到每一个开关周期。

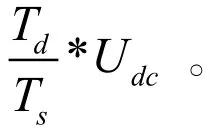
其中，Ua为实际的输出电压值，为理论的输出电压值。由分析可知,死区所造成的电压畸变和电流的极性（ ia＞ 0和 ia＜ 0）直接相关,而和电流的大小无关,并且，死区产生的偏差电压∆U的极性总是与负载电流相反,因此总是减小实际电流。那么，只要在这个周期中给输出电压补偿一个与之大小相等，方向相反的方波电压即可。

（2）坐标变换电流反馈死区补偿的实现

坐标变换电流反馈死区补偿的实现步骤如下：

首先，将采样电流从三相静止坐标系A-B-C变换到两相同步旋转d-q坐标系系下，在这个坐标系下，电流表现为直流量，对它进行滤波处理。

其次，将滤波后的电流从d-q坐标系变换回三相静止坐标系A-B-C，并对它进行极性检测。

再次，根据电流极性计算出每一相的补偿电压大小，并折算成补偿信号（后面有详细推导过程）。

最后，将补偿信号叠加到SVPWM输出的调制波形中。

坐标变换电流反馈法的实现流程示意图如图3所示。

图3 坐标变换电流反馈法的实现流程Fig. 3 Flow of implementation of coordinate transformation current feedback method

根据以上分析结合式（1）可得：A相的补偿电压可表示为式（2）所示：

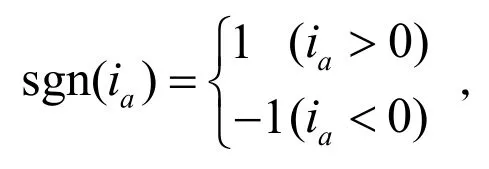
要注意的一点是：当把此补偿电压叠加到SVPWM输出的调制波上时需要进行相应的折算。根据SPWM的调制原理可知，调制电压与输出电压存在如下关系：

其中，Um为调制波幅值， U∆为三角载波幅值，Udc为直流母线电压， Uout为输出电压。

式（2）中的补偿电压Uabu相当于（3）式中的Uout，当把它叠加到调制波上时需要反向折算，折算后的补偿电压为：

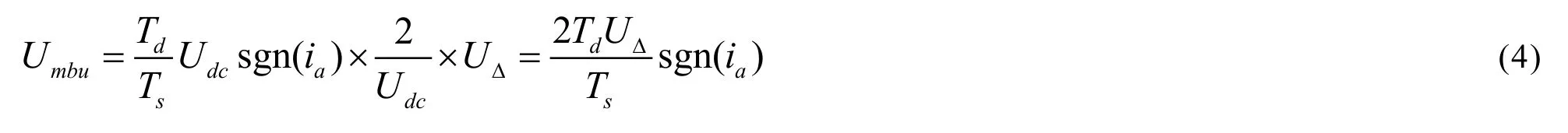
异步电机死区补偿SVPWM矢量控制系统结构如图4所示。

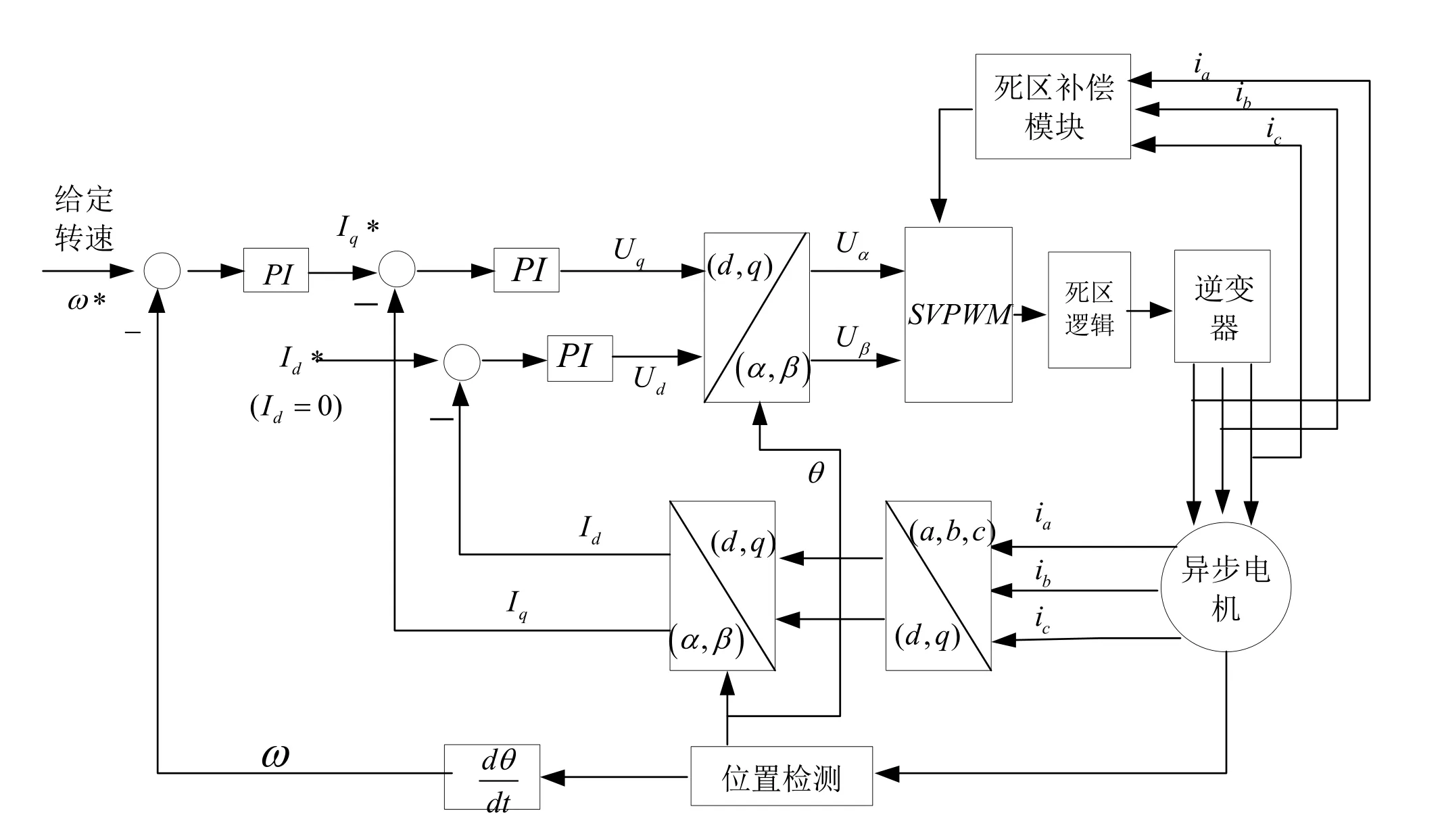
图4 异步电机死区补偿SVPWM矢量控制系统Fig.4 Asynchronous motor dead zone compensation SVPWM vector control system

图5 异步电机死区补偿SVPWM矢量控制系统仿真模型Fig.5 Simulation model of asynchronous motor dead zone compensation SVPWM vector control system

3 仿真结果

在Matlab/Simulink环境下建立带死区补偿的异步电机矢量控制系统模型如图5所示。

在系统中仿真参数设定如下：异步电机参数分别为： Rs= 0.078Ω， Rr= 0.04Ω， Ls= 0.000657，Lr= 0.000799 H ， Lr= 0.020253 H ，P=4。载波周期 Ts= 5e -4 s （频率2 kHz），负载 Te= 25 N.m ，死区时间 Td= 2 e − 5s ，直流电压 Udc=1500 V。

图6 (a) 补偿前电机电流Fig. 6 (a) Motor current before compensation

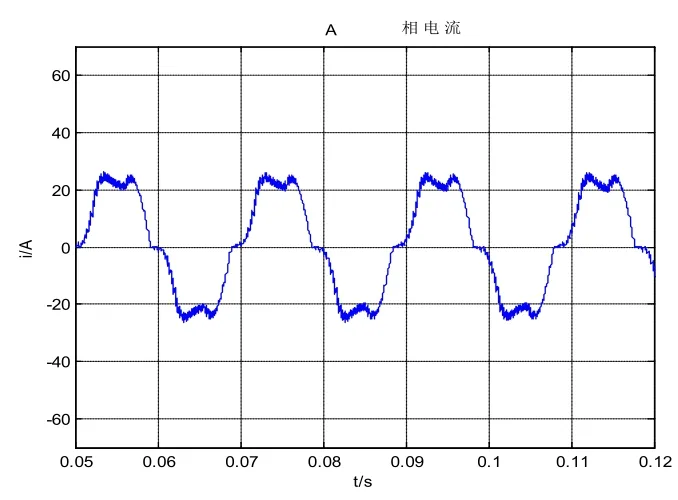
图6 (b) 补偿前A相电流Fig. 6(b) Compensating A phase current

图6 (c) 补偿前转矩Fig. 6 (c) Torque before compensation

图7 (a) 补偿后电机电流Fig. 7 (a) Motor current after compensation

图7 (b) 补偿后A相电流Fig.7 (b) A-phase current after compensation

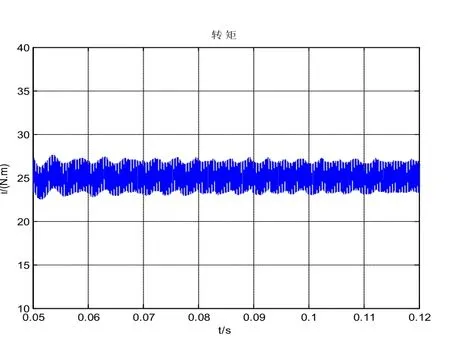
图7 (c) 补偿后转矩Fig.7 (c) Torque after compensation

从仿真结果图6（a）～（c）和图7（a）～（c）可以得出：补偿前与补偿后，采用本文提出的坐标变换电流反馈死区补偿法进行补偿，异步电机定子电流波形质量得到了较大提升，电流正弦度明显改善，转矩脉动也得到了明显抑制。

4 结语

本文详细分析了死区效应产生的原因及影响，并推导出了死区效应引起的逆变器输出平均误差电压的表达式。通过深入剖析平均误差电压产生的本质和电流反馈法的原理，并结合SVPWM的原理，总结出坐标变换电流反馈死区补偿方法。通过仿真实验证明了该方法能有效地改善逆变器输出电流的正弦性，减少转矩脉动，提高系统性能，具有一定的实用价值。

但同时，坐标变换电流反馈死区补偿也存在着不足之处：通过坐标变换对电流进行低通滤波处理，虽然不会引起系统的的稳态误差，但难免会对系统的瞬态响应产生一点影响，关于这方面的研究有待进一步深入。

[1] 吴茂刚, 赵荣祥, 汤新舟. 矢量控制永磁同步电动机低速轻载运行的研究[J]. 电工技术学报, 2005, 20(7): 87-92.WU Mao-gang, ZHAO Rong-xiang, TANG Xin-zhou. Research on low speed and light load operation of vector control permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2005, 20(7): 87-92.

[2] TAGHIRAD H D, ABEDI N, NOOHI E. A new sensorless vector control method for permanent magnet synchronous motor without velocity estimator[C]// International Workshop on Advanced Motion Control. IEEE, 2002:242-246.

[3] BEN-BRAHIM L. On the compensation of dead time and zero-current crossing for a PWM-inverter-controlled AC servo drive[J]. Industrial Electronics IEEE Transactions on, 2004, 51(5): 1113-1118.

[4] JEONG S, PARK M. The analysis and compensation of dead-time effects in PWM inverters[J]. IEEE Trans on Industrial Electronics, 1991,38(2): 108-114.

[5] 孙向东, 钟彦儒. 一种新颖的死区补偿时间测量方法[J]. 中国电机工程学报, 2003, 23(2): 103-107.SUN Xiang-dong, ZHONG Yan-ru. A novel dead-zone compensation time measurement method [J]. Chinese Journal of Electrical Engineering, 2003, 23(2): 103-107.

[6] 彭赛庄, 朱晓青, 秦斌, 等. 基于SVPWM控制的地铁再生制动能量吸收系统的仿真研究[J]. 新型工业化, 2016, 5(3): 20-27.PENG Sai-zhuang, ZHU xiao-qing, QIN Bin, et al. Simulation Research of Subway Regenerative Braking Energy Absorption System Based on SVPWM Control [J]. The Journal of New Industrialization, 2016, 5(3): 20-27.

[7] 陈强, 余梦梦, 魏倩. 带有死区和摩擦补偿的机械臂伺服系统自适应神经网络控制 [J]. 新型工业化, 2016, 6(8): 1-8.CHEN Qiang, YU Meng-meng, WEI Qian. Adaptive neural network control of manipulator servo system with dead zone and friction compensation[J]. The Journal of New Industrialization, 2016,6(8):1-8.

[8] URASAKI N, SENJYU T, UEZATO K, et al. On-line dead-time compensation method for permanent magnet synchronous motor drive[C]//IEEE International Conference on Industrial Technology, 2002. IEEE Icit. IEEE, 2002(1):268-273.

[9] OLIVEIRA A C, JACOBINA C B, LIMA A M N, et al. Dead-time compensation in the zero-crossing current region[C]// Power Electronics Specialist Conference, 2003. Pesc '03. 2003 IEEE. IEEE, 2003(4): 1937-1942.

[10] JONG W C, SEUNG K S. A new compensation strategy reducing voltage current distortion in PWM VSI systems operating with low output voltages[J]. IEEE Trans. on IndustryApplications, 1995, 31(5): 1001-1008.

[12] CHOI J, SUL S. Inverter output voltage synthesis using novel dead time compensation. IEEE Transactions on Power Electronics, 1996,11(2): 221-227.

[13] WU C M, LAU W H, CHUNG S H. Analytical technique for calculating the output harmonics of an H-bridge inverter with dead time[J].IEEE Transactions on Circuits & Systems I Fundamental Theory & Applications, 2002, 46(5): 617-627.

[14] CHOI J S, YOO J Y, LIM S W, et al. A novel dead time minimization algorithm of the PWM inverter[C]// Industry Applications Conference,1999. Thirty-Fourth Ias Meeting. Conference Record of the. IEEE Xplore, 1999(4): 2188-2193.

[15] ATTAIANESE C, TOMASSO G. Predictive compensation of dead time effects in VSI feeding induction motors[J]. IEEE Trans. on Industry Application, 2001, 37(3): 856-863.