改进的组合式L形钢管混凝土长柱轴压性能非线性分析

曹 兵，王义俊，张金轮，黄 博，杜怡韩，黄 俊

(1.安徽工程大学 建筑工程学院，安徽 芜湖 241000；2.武汉理工大学 土木工程与建筑学院，湖北 武汉 430070)

钢管混凝土由于具有承载力高、抗震性能好、施工方便等优点在高层以及超高层建筑中得到广泛应用.钢管混凝土发挥自身优良性能的关键在于钢管与混凝土之间的协同工作.国内外学者提出了多种截面形式的钢管混凝土，已有的研究成果表明，钢管截面形式不同，钢管混凝土表现出来的协同工作性能也有所区别，钢管约束作用越强，两者之间的协同工作性能越好[1-3].目前对圆、方和矩形钢管混凝土长柱的研究相对较多[4-7]，而对异形钢管混凝土长柱的研究相对较少.文献[8-9]对多室式异形钢管混凝土中长柱轴压性能进行了研究，在参数分析的基础上建立中长柱稳定系数以及稳定承载力计算公式.文献[10]对T形钢管混凝土长柱力学性能进行了研究，在参数分析的基础上建立中长柱承载力简化计算方法.文献[11]在现有异形钢管混凝土基础上，提出了一种改进的组合式异形钢管混凝土，其异形钢管直接由矩(或方)形钢管和U形钢管焊接形成，并对这种改进的组合式异形钢管混凝土轴压力学性能进行了试验研究，试验过程中考虑的影响因素相对较少且主要集中在短柱方面.在上述研究的基础上，拟对改进的组合式L形钢管混凝土长柱力学性能做进一步研究，并提出在改进的组合式异形钢管混凝土中的部分矩形钢管中设置支撑钢板，以解决宽厚比较大的钢管过早屈曲的问题，但是支撑钢板对其轴压性能的影响并未研究.以改进的组合式L形钢管混凝土长柱为对象，采用ABAQUS软件对其轴压力学性能进行了研究，并与已有的试验结果进行对比，验证了有限元模型的可靠性，主要分析了钢管厚度、混凝土强度、支撑钢板设置、长细比等因素对其轴压力学性能的影响，最后从轴压荷载-变形关系曲线以及钢管、钢板、混凝土之间的相互作用等方面分析了该类长柱轴压的工作机理，为该类柱在工程上的应用提供理论依据.

1 有限元模型

1.1 有限元模型设计

设计32个改进的组合式L形钢管混凝土长柱轴压试件，试件上、下两端各设置一块端板，端板尺寸与试件截面尺寸相同，端板、支撑钢板和钢管均采用相同钢材，支撑钢板与钢管厚度相同，核心混凝土均采用自密实微膨胀混凝土，试件截面形式及试件编号分别如图1和表1所示.

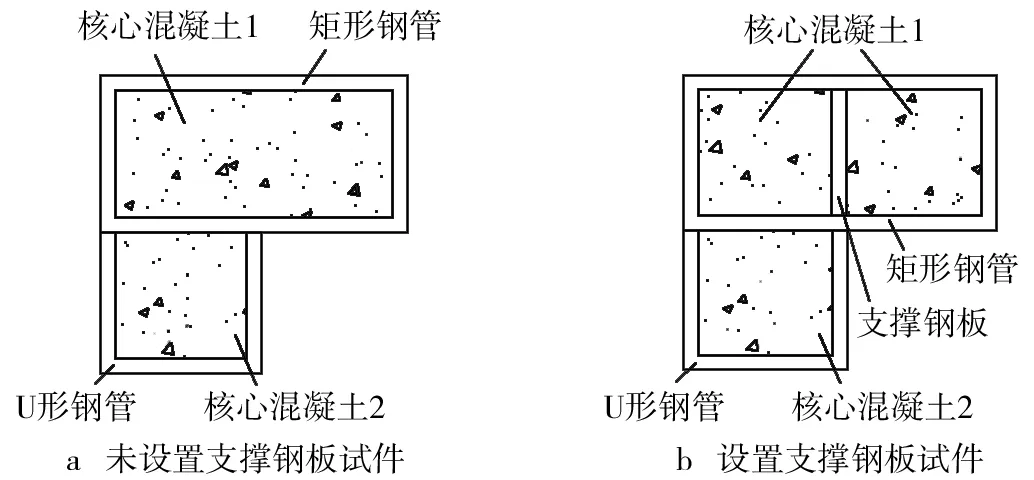
图1 试件截面形式

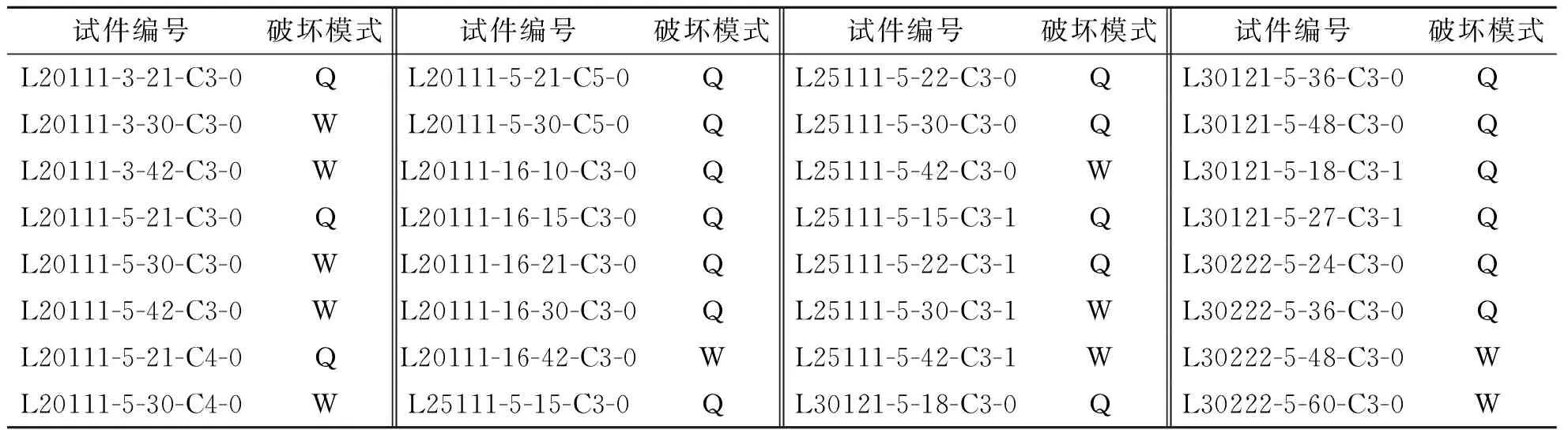
试件编号破坏模式试件编号破坏模式试件编号破坏模式试件编号破坏模式L20111-3-21-C3-0QL20111-5-21-C5-0QL25111-5-22-C3-0QL30121-5-36-C3-0QL20111-3-30-C3-0WL20111-5-30-C5-0QL25111-5-30-C3-0QL30121-5-48-C3-0QL20111-3-42-C3-0WL20111-16-10-C3-0QL25111-5-42-C3-0WL30121-5-18-C3-1QL20111-5-21-C3-0QL20111-16-15-C3-0QL25111-5-15-C3-1QL30121-5-27-C3-1QL20111-5-30-C3-0WL20111-16-21-C3-0QL25111-5-22-C3-1QL30222-5-24-C3-0QL20111-5-42-C3-0WL20111-16-30-C3-0QL25111-5-30-C3-1WL30222-5-36-C3-0QL20111-5-21-C4-0QL20111-16-42-C3-0WL25111-5-42-C3-1WL30222-5-48-C3-0WL20111-5-30-C4-0WL25111-5-15-C3-0QL30121-5-18-C3-0QL30222-5-60-C3-0W

注：L20111-3-21-C3-0中L表示试件截面形式为L形，20111表示试件采用矩形钢管尺寸为200 mm×100 mm，U形钢管尺寸为100 mm×100 mm，3表示钢管厚度为3 mm，21表示试件长度为2 100 mm，C3表示试件采用混凝土强度等级为C30，0表示试件未设置支撑钢板(即支撑钢板数量为0)，其他试件编号意义以此类推；表中Q表示试件破坏形态为强度破坏，W表示试件破坏形态为弯曲破坏．

1.2 材料本构关系模型

钢材主要采用Q235低碳钢，钢材的材料模型采用ABAQUS中自带的等向弹塑性本构模型，满足von Mises屈服准则，能够较好地描述低碳钢弹塑性性能，其计算表达式为：

(1)

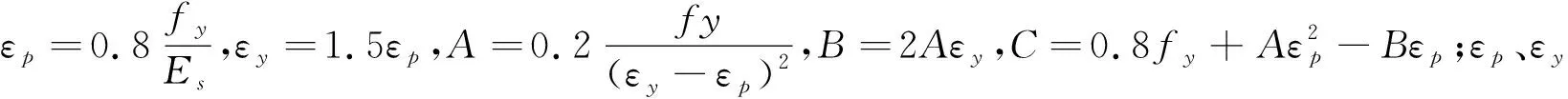
选取核心混凝土本构关系时，需要充分考虑钢管的约束作用影响.核心混凝土的材料模型采用塑性损伤本构模型，受拉本构关系采用Schneider应力-应变关系，其计算表达式为[12]：

(2)

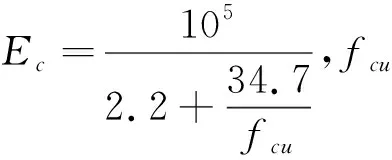
受压本构关系采用修正后的Mander应力-应变关系，其计算表达式为[13-14]：

(3)

式中，εcc为约束混凝土峰值应变；σcc为约束混凝土峰值应力；r为曲线上升段形状参数；k为曲线下降段形状参数；上述参数计算公式详见文献[13-14].

1.3 单元类型及接触类型

图2 有限元模型

端板、钢管、核心混凝土以及支撑钢板均采用三维实体建模方法，其单元类型均采用8节点三维非协调单元(C3D8I).矩(或方)形钢管和U形钢管之间以及支撑钢板和矩形钢管之间直接采用“Tie”约束，钢管与核心混凝土之间以及支撑钢板与核心混凝土之间均采用通用接触模型.法向接触采用“Hard接触”，接触后可以分离，但不允许相互渗透.切向接触采用库伦摩擦模型，摩擦系数取0.25.端板与试件之间亦采用通用接触模型，仅设置法向接触，法向接触采用“Hard接触”，接触后不允许分离.

1.4 边界条件及加载方式

根据试件实际的边界条件，约束下端板x、y、z三个方向的自由度，约束上端板x、y两个方向的自由度，释放z方向的自由度，在上端板沿着z方向施加位移荷载.为了更加真实地反映改进的组合式异形钢管混凝土长柱的受力状态，施加位移荷载时考虑千分之一试件长度的初始偏心距.有限元模型如图2所示.

1.5 有限元模型验证

为了验证所建立的有限元模型的可靠性，对文献[11]中的部分试件进行了数值计算，获得了试件荷载-轴向位移关系曲线，其有限元计算结果与试验结果对比如图3所示.从图3可以看出，有限元计算结果与试验结果吻合较好，由此表明所建立的有限元模型具有一定的可靠性.

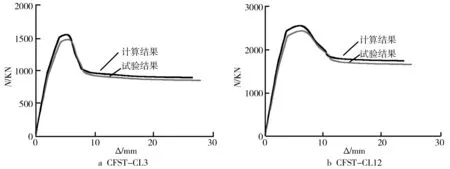
图3 有限元计算结果与试验结果对比

图4 试件典型破坏形态

2 有限元计算结果及分析

2.1 破坏形态分析

有限元模拟得到的改进的组合式L形钢管混凝土长柱轴压破坏形态分类如图4所示，各试件具体破坏形态如表1所示.从表1及图4可以看出，部分试件由于在矩形钢管中设置了支撑钢板，减小了钢管长边宽厚比，使矩形钢管对核心混凝土的约束作用近似于方形钢管，产生了较强的约束作用，进一步提高了试件材料的强度，但试件长细比较大，二阶效应表现较为明显，导致试件中部发生较大幅度的侧向弯曲，从而发生整体弯曲失稳破坏；部分试件由于未在矩形钢管中设置支撑钢板，矩形钢管对核心混凝土的约束作用相对较弱，同时试件长细比较大，试件中部不仅发生了较大幅度侧向弯曲，而且试件中部钢管也发生了较大的鼓曲；部分试件端部钢管发生鼓曲现象，核心混凝土产生较大横向变形，试件因材料强度不足而发生强度破坏.由此可见，改进的组合式L形钢管混凝土长柱轴压破坏形态主要分为弯曲破坏和强度破坏两类.

2.2 荷载-轴向位移关系曲线

有限元计算得到改进的组合式L形钢管混凝土长柱轴压荷载-轴向位移关系曲线如图5所示，图5中仅列出了部分试件轴压荷载-轴向位移关系曲线在不同参数下的对比情况，其他试件轴压荷载-轴向位移关系曲线在不同参数下的变化规律基本类似，不再赘述.从图5可以看出，各组试件轴压荷载-轴向位移关系曲线基本类似，主要分为三个阶段，即弹性阶段、弹塑性阶段和下降阶段；随着试件长细比的增大和钢管厚度的减小，曲线弹性阶段和弹塑性阶段的轴压刚度都有减小的趋势，承载力和下降阶段的平缓程度也进一步降低，钢管达到一定厚度时，曲线下降段基本趋于平缓或略有上升；混凝土强度和设置支撑钢板对曲线影响相对较小，随着混凝土强度的增加和支撑钢板的设置，曲线弹性阶段和弹塑性阶段的轴压刚度基本不变，但承载力有一定程度的提高.

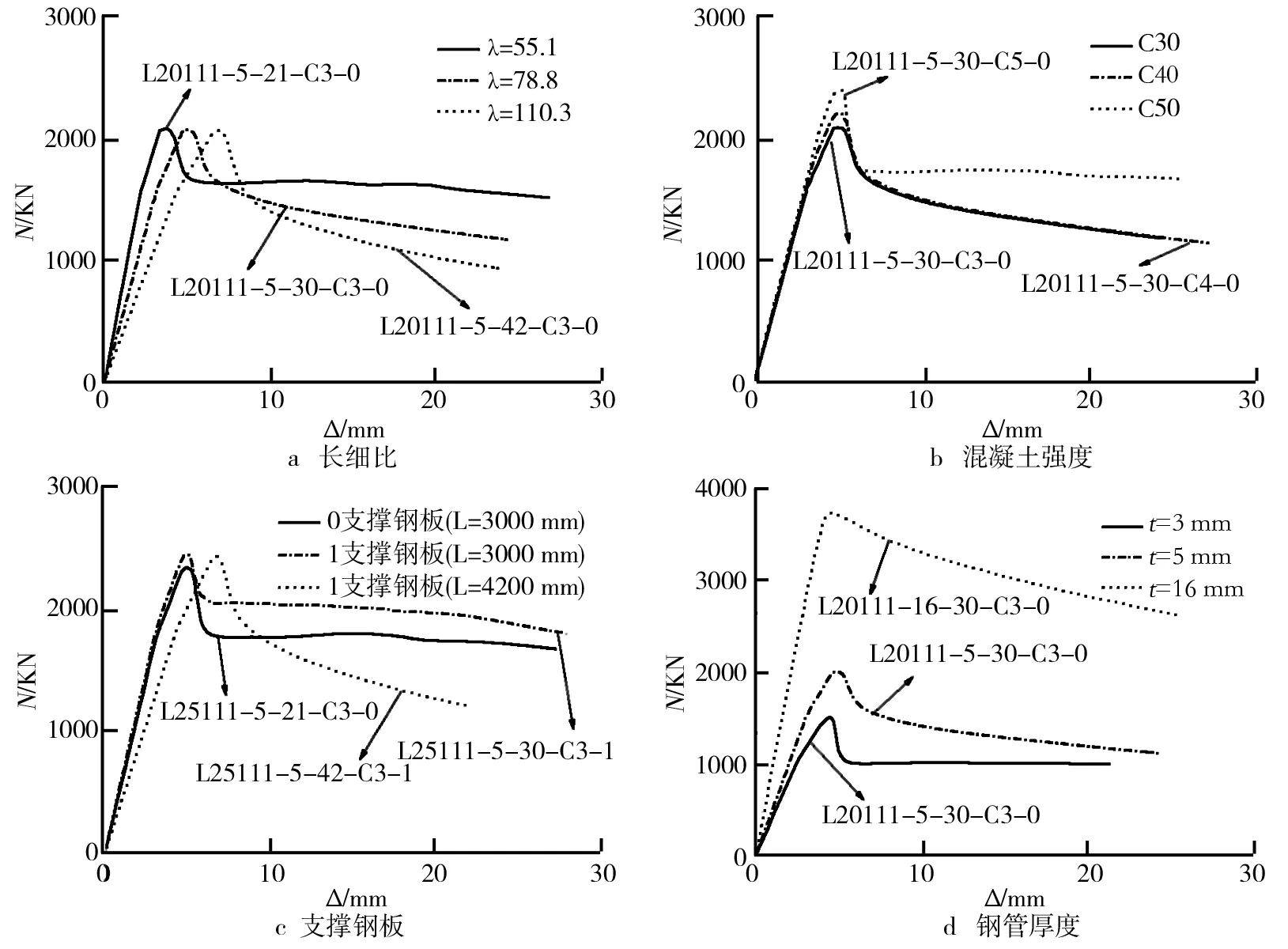
图5 荷载-轴向位移关系曲线

2.3 荷载-侧向挠度关系曲线

有限元计算得到的改进的组合式L形钢管混凝土长柱轴压荷载-侧向挠度关系曲线如图6所示.图6中仅列出了部分试件轴压荷载-侧向挠度关系曲线在不同参数下的对比情况，由于其他试件轴压荷载-侧向挠度关系曲线在不同参数下的变化规律基本类似，不再赘述.从图6中可以看出，各试件轴压荷载-侧向挠度关系曲线主要分为两大阶段，即上升段和下降段，其中上升段包含弹性阶段和屈服阶段，长细比、支撑钢板的设置及钢管厚度对轴压荷载-侧向挠度关系曲线影响较大.弹性阶段各试件轴压荷载与侧向挠度主要呈线性关系，曲线斜率相差不大，钢管、支撑钢板和混凝土之间基本处于单独受力状态，钢管、支撑钢板和混凝土之间的相互作用较小，弹性阶段末所对应的轴压荷载约为极限轴压荷载的75%～85%之间，所对应的侧向挠度约在0.5～1.5 mm之间.屈服阶段各试件轴压荷载与侧向挠度主要呈非线性关系，侧向挠度增加速率比轴压荷载增加速率要快，达到极限轴压荷载时，侧向挠度基本达到了3～6 mm.下降段各试件轴压荷载出现下降现象，主要是由于试件产生了较大的侧向挠度，进而产生了较大的附加弯矩，从而丧失稳定.

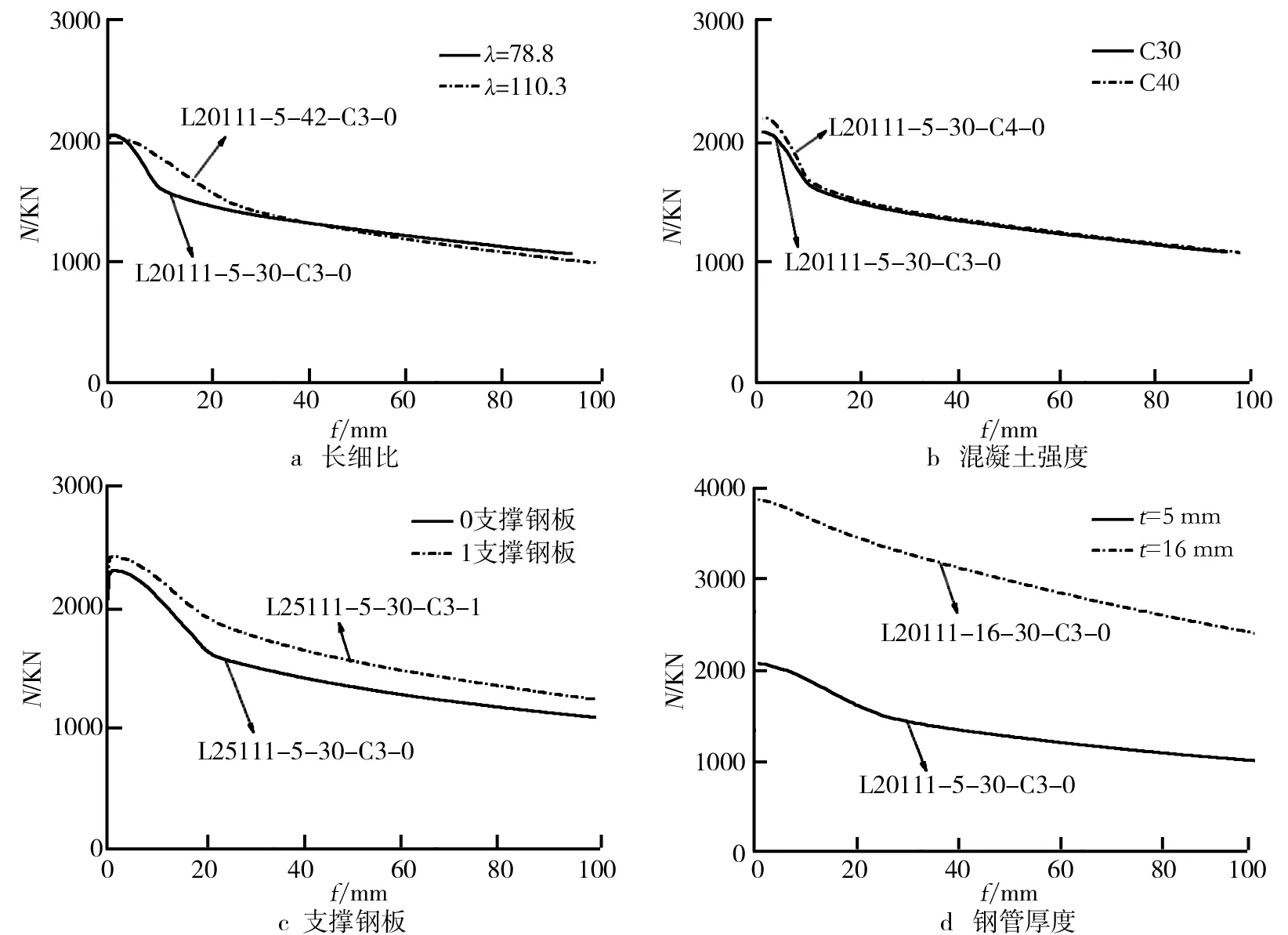
图6 荷载-侧向挠度关系曲线

2.4 钢管、支撑钢板以及核心混凝土相互作用

为了说明钢管、支撑钢板以及核心混凝土之间的相互作用，以试件L20111-5-30-C3-0(未设置支撑钢板)、L25111-5-30-C3-1(设置了支撑钢板)为例加以分析，其他试件相互作用关系基本类似，不再赘述.

(1)钢管、支撑钢板及核心混凝土轴压荷载分配分析.有限元计算得到的改进的组合式L形钢管混凝土长柱的钢管、支撑钢板及核心混凝土轴压荷载分配情况如图7所示.从图7a可以看出，对于未设置支撑钢板的试件，从加载开始至75%峰值荷载时，钢管和核心混凝土承担轴压荷载比例变化不大，钢管和核心混凝土承担轴压荷载比例分别为52.7%和47.3%，其中，矩形钢管和U形钢管承担轴压荷载比例分别约为34.5%和18.2%，核心混凝土1和核心混凝土2承担轴压荷载比例分别约为31.6%和15.7%；达到峰值荷载时，钢管承担轴压荷载比例有所增加，核心混凝土承担轴压荷载比例有所减少，钢管和核心混凝土承担轴压荷载比例分别为59.2%和40.8%，其中，矩形钢管和U形钢管承担轴压荷载比例分别约为38.6%和20.6%，核心混凝土1和核心混凝土2承担轴压荷载比例分别约为27.2%和13.6%；达到峰值荷载后，矩形钢管承担轴压荷载比例基本变化不大，U形钢管承担轴压荷载比例增加幅度较大，核心混凝土承担轴压荷载比例呈逐渐减小状态.从图7b可以看出，对于设置支撑钢板的试件，从加载开始至75%峰值荷载时，钢管、支撑钢板和核心混凝土承担轴压荷载比例变化不大，钢管、支撑钢板和核心混凝土承担轴压荷载比例分别为50.7%、4.1%和45.2%，其中，矩形钢管、U形钢管承担轴压荷载比例分别为34.5%、16.2%，核心混凝土1和核心混凝土2承担轴压荷载比例分别为32.1%和13.1%；达到峰值荷载时，钢管承担轴压荷载比例有所增加，支撑钢板承担轴压荷载比例提高幅度相对较小，核心混凝土承担轴压荷载比例有所减小，钢管、支撑钢板和核心混凝土承担轴压荷载比例分别为55.2%、4.6%和40.2%，其中，矩形钢管和U形钢管承担轴压荷载比例分别约为37.3%和17.9%，核心混凝土1和核心混凝土2承担轴压荷载比例分别约为28.7%和11.5%；达到峰值荷载后，钢管承担轴压荷载比例呈逐渐增大状态，其中矩形钢管承担轴压荷载比例增加幅度较大，支撑钢板承担轴压荷载比例基本变化不大，核心混凝土承担轴压荷载比例呈逐渐减小状态，其中核心混凝土1承担轴压荷载比例下降幅度较大.由此表明，在矩形钢管中设置支撑钢板有效地延缓了矩形钢管的局部屈曲，增强了矩形钢管对核心混凝土1的约束作用，进一步提高了核心混凝土1的承载能力.

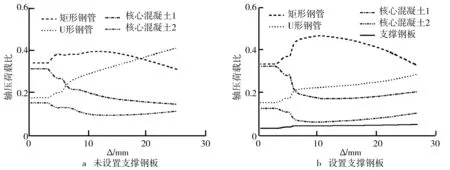
图7 钢管、支撑钢板及核心混凝土轴压荷载分配

(2)钢管、支撑钢板与核心混凝土接触压力分析.有限元计算得到的改进的组合式L形钢管混凝土长柱各面接触压力与轴压荷载关系曲线如图8所示.从图8a中可以看出，对于未设置支撑钢板的试件，从开始加载至90%峰值荷载时，试件各面接触压力与轴压荷载主要呈现出线性关系，而且各面接触压力均较小，A面、B面、C面和D面接触压力分别为0.066 MPa、0.060 MPa、0.053 MPa、0.268 MPa；加载至峰值荷载时，试件各面接触压力与轴压荷载则不再呈线性关系，接触压力的增长速率明显高于轴压荷载增长速率，各面接触压力有较大增加，A面、B面、C面和D面接触压力分别为0.236 MPa、0.435 MPa、0.351 MPa、0.341 MPa；达到峰值荷载以后，各面接触压力急剧增加，其中A面接触压力的增加幅度相比B面、C面、D面要小；由此表明宽厚比较大的A面对核心混凝土约束作用要小.从图8b中可以看出，对于设置支撑钢板的试件，从开始加载至90%峰值荷载时，试件各面接触压力与轴压荷载主要呈线性变化，而且各面接触压力也相对较小，A面、B面、C面和D面接触压力分别为0.062 MPa、0.079 MPa、0.114 MPa、0.008 MPa；加载至峰值荷载时，试件各面接触压力与轴压荷载主要呈曲线变化，接触压力的增长速率比轴压荷载增长速率要快，各面接触压力有较大程度增加，A面、B面、C面和D面接触压力分别为0.317 MPa、0.521 MPa、0.499 MPa、0.332 MPa；达到峰值荷载以后，各面接触压力急剧增加，但A面、B面、C面和D面接触压力增长幅度基本相同；相比于未设置支撑钢板的试件，设置支撑钢板的试件各面接触压力更加均匀，由此表明，在矩形钢管中设置支撑钢板能够有效减小钢管长边的宽厚比，使钢管各边的宽厚比基本相同，从而提高钢管对核心混凝土的约束作用，即钢管宽厚比越小，其约束作用越强.

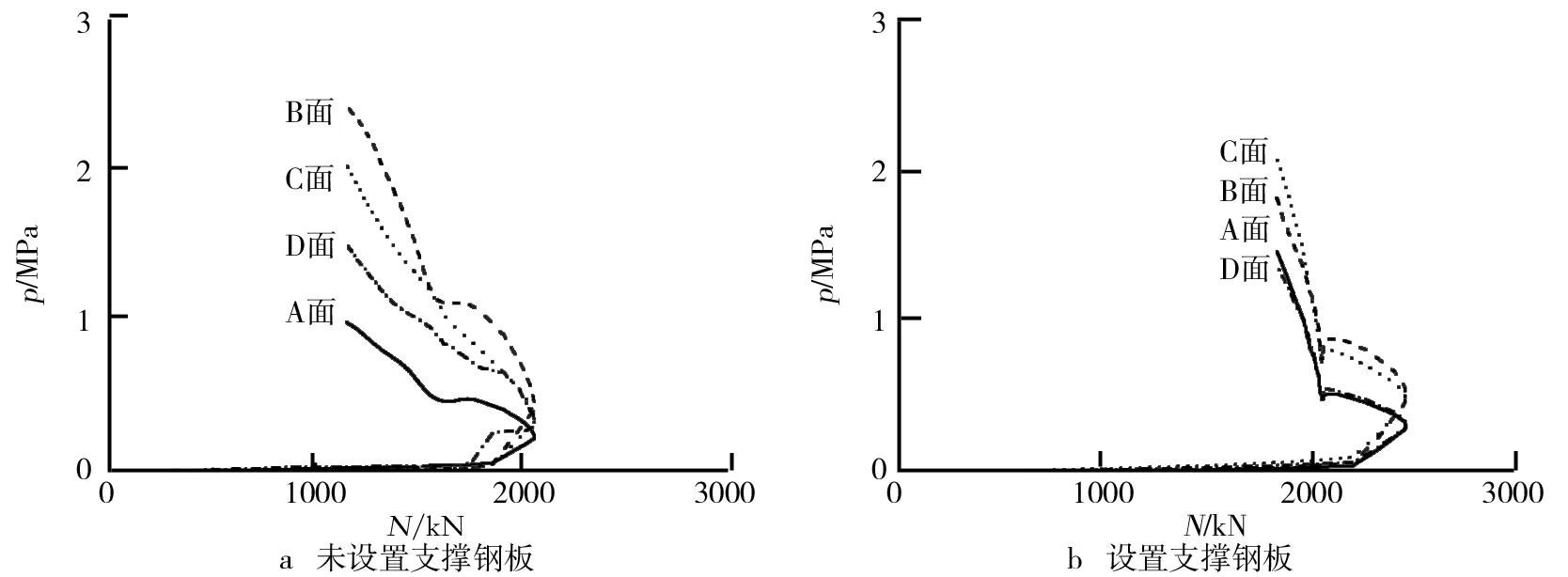
图8 接触压力与轴压荷载关系曲线

3 轴压稳定承载力计算

采用文献[15]中轴压稳定承载力计算公式(1)和文献[16]中轴压稳定承载力计算公式(11)对改进的组合式L形钢管混凝土长柱轴压稳定承载力进行了计算，公式理论计算值与有限元计算值的比值如表2所示.从表2中可以看出，公式(1)的理论计算值的准确性高于公式(11)，但公式(1)的理论计算值小于有限元计算值，与有限元计算值存在一定的差距，轴压稳定承载力计算公式需做进一步修正.由于篇幅有限，在后续论文中将给出改进的组合式L形钢管混凝土长柱轴压稳定承载力计算方法的研究成果.

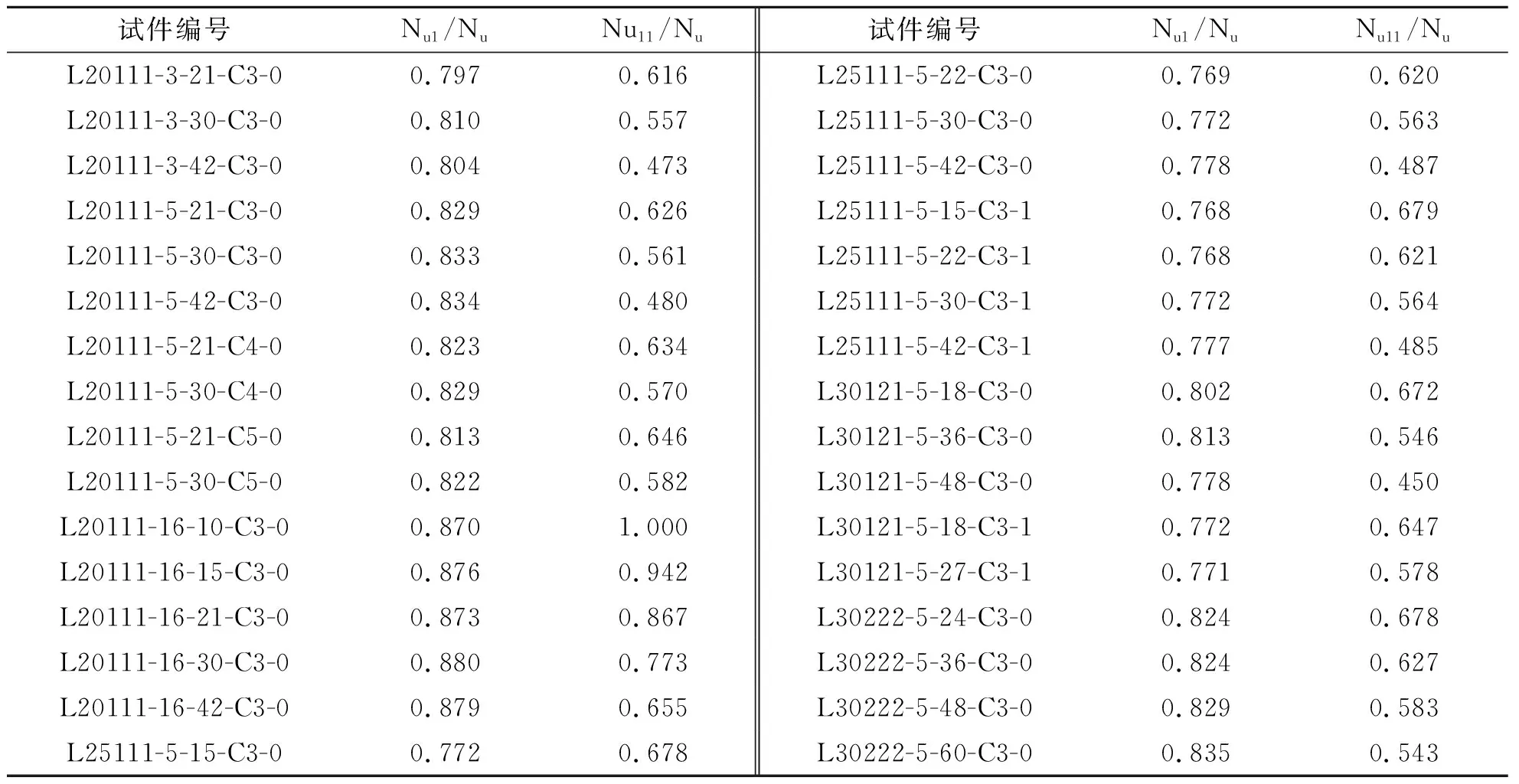
表2 试件轴压稳定承载力公式理论计算值与有限元计算值比值

注：表中Nu1、Nu11和Nu分别为试件轴压稳定承载力公式(1)、公式(11)理论计算值和有限元计算值.

4 结论

在试验研究的基础上采用有限元软件ABAQUS对改进的组合式L形钢管混凝土长柱轴压性能进行了非线性分析，可得到以下结论：试件荷载-轴向位移关系曲线有限元计算结果与试验结果吻合较好，所建立的有限元模型具有一定的可靠性；试件破坏形态主要分为弯曲破坏和强度破坏.钢管厚度及长细比对试件荷载-轴向位移关系曲线影响较大；混凝土强度及支撑钢板设置对试件荷载-轴向位移关系曲线影响较小；长细比、支撑钢板设置及钢管厚度对荷载-侧向挠度关系曲线影响较大.从加载开始至75%峰值荷载时，钢管和核心混凝土承担轴压荷载比例变化不大；达到峰值荷载时，钢管承担轴压荷载比例有所增加，核心混凝土承担轴压荷载比例有所减少；相比于未设置支撑钢板的试件，设置支撑钢板的试件各面接触压力更加均匀；在矩形钢管中设置支撑钢板能够提高钢管对核心混凝土的约束作用.轴压稳定承载力计算公式(1)、公式(11)的理论计算值均小于有限元计算值，轴压稳定承载力计算公式需做修正.

[1] 张向冈,陈宗平,薛建阳,等.钢管再生混凝土轴压长柱试验研究及力学性能分析[J].建筑结构学报,2012,33(9):12-20.

[2] 徐羊,姚勇,张兆强,等.方钢管再生混凝土长柱偏心受压力学性能研究[J].建筑结构,2016,46(9):69-74.

[3] K KONNO,Y SATO,Y KAKUTA,et al.Property of recycled concrete column encased by steel tube subjected to axial compression[J].Transactions of the Japan Concrete Institute,1997,19(2):231-238.

[4] 徐礼华,徐方舟,周鹏华,等.钢管自应力自密实高强混凝土中长柱受压性能试验研究[J].土木工程学报,2016,49(11):26-35.

[5] J Y RICHARD LIEW,D X XIONG.Ultra-high strength concrete filled composite columns for multi-storey building construction[J].Advances in Structural Engineering,2012,15(9):1 487-1 503.

[6] J M PORTOLES,E SERRA,M L ROMERO.Influence of ultrahigh strength infill in slender concrete-filled steel tubular columns[J].Journal of Constructional Steel Research,2013,86(7):107-114.

[7] 陶毅,张海镇,史庆轩,等.内置FRP约束混凝土的方钢管混凝土轴压承载力[J].土木建筑与环境工程,2017,39(2):43-49.

[8] 屠永清,刘林林,叶英华.多室式钢管混凝土T形中长柱轴压性能研究[J].土木工程学报,2012,45(9):27-35.

[9] 马丽娅,屠永清.多室式钢管混凝土组合L形柱轴压性能有限元分析[J].建筑结构学报,2013,34(S1):306-313.

[10] 雷敏,沈祖炎,李元齐,等.T形钢管混凝土单向偏压长柱力学性能分析[J].同济大学学报：自然科学版,2016,44(2):207-212.

[11] 戴绍斌,曹兵,黄俊.改进的组合式L形钢管混凝土柱力学性能试验[J].哈尔滨工业大学学报,2015,47(3):122-128.

[12] S P SCHNEIDER.Axially loaded concrete-filled steel tubes[J].Journal of Structural Engineering，1998,124(10):1 125-1 138.

[13] J B MANDER,M J N PRIESTLEY,R PARK.Theoretical stress-strain model for confined concrete[J].Journal of Structural Engineering,1988,114(8):1 807-1 826.

[14] 曹兵,戴绍,黄俊.改进组合式L形钢管中核心混凝土应力-应变关系[J].福州大学学报,2016,44(4):465-471.

[15] 杜国锋,宋鑫,张志忠,等.内置钢骨组合L形截面钢管混凝土中长柱轴心受压试验研究[J].四川大学学报:工程科学版,2013,45(5):43-50.

[16] 屠永清,文千山.L形钢管混凝土柱轴压承载力计算[J].建筑结构学报,2013,34(S1):314-320.