借“画图”之力 点“思维”之光——以苏教版教材数学解决问题教学为例

江苏东海县实验小学（222300） 张 琪

画图是小学生数学学习中必备的解题能力，画图能借助几何直观把复杂的数学问题变得简明形象，有助于学生探索解决问题的思路，在整个数学学习过程中起着重要的作用。从学生的认知特点和数学学习的角度而言，动手操作具有直观形象性，随着学生抽象逻辑思维的发展，动手操作可以慢慢转变为用简洁抽象的数学符号来表述，而且画图的直观形象可以让学生从手感、触感、视觉等角度进行全方位感受，利于学生数学思维的发展。

在当前的数学课堂上，教师仅仅把画图当作分析问题的策略，大多在讲解新课或习题时自己画图，而忽略了学生主动借助画图解决问题的体验。因此，教师要逐步培养学生读图、画图、析图的能力，在平时的数学学习中形成画图意识。下面我结合多年的教学经验，谈谈如何向学生渗透画图的策略。

一、借助画图策略，表征题目意思

学生的认知起点不是一张白纸，他们对生活的认知就涵盖了很多数学数量关系，教师在教学时要以此为契机，将数学中的知识和生活联系起来，并让学生用画图的方式记录在白纸上，以此帮助学生更好地解决问题。

例如，在教学苏教版教材四年级下册第六单元“运算律之相遇问题”一课时，为了让学生理解题目中的“相对、同时、相遇、相距”这四个词语的意思，我先让学生利用生活经验进行表演，再将表演的过程中用图记录下来。

师（出示题目：小张和小李同时从家出发走向电影院，小张每分钟走80米，小李每分钟走60米，5分钟后，两人在电影院门口相遇，他们两家相距多少米？）：这里的“相遇”是什么意思？

生1：“相遇”就是两个人遇到了。

师：请两位同学来演示一下什么是“相遇”。

（两个学生从各自的位置走到一起后停止）

师：大家能画图把刚才两位同学的演示过程记录下来吗？再试着写一写算式。

生2：我先画一条线段表示从小张家到小李家，这边的点表示5分钟后两人相遇的电影院。我先算出小张5分钟走的路程是80×5=400（米），再算出小李5分钟走的路程是60×5=300（米），所以他们两家相距400+300=700（米）。

生3：我通过画图发现小张和小李两人1分钟走的路程是80+60=140（米），所以5分钟他们两人走的路程是 140×5=700（米）。

师：大家能理解生2的400米、300米、700米是线段图上的哪一段吗？

在这个教学片段中，教师从学生的生活起点和知识起点出发，唤起学生原有的认知，在出示例题后，用学生实际走路演绎“相遇”，将模拟中走的路程和题目条件一一对应，借助生活实际进行沟通，加深学生对“相遇”这个关键词的认识，最后借助画图和课件进一步加深学生对“80+60”的理解，启迪学生借助线段图演绎和理解题意，并进行数学思考，很好地培养了学生的画图意识。

二、借助画图策略，寻找解题思路

小学生多以形象思维为主，其抽象思维发展还不完整，特别是中低年级学生。中低年级学生对一些复杂的语句及抽象的数量关系不理解，导致解决问题难以入手，而示意图搭建了形象思维与抽象思维之间的桥梁，便于学生找到解决数学问题的突破口。

例如，在教学苏教版教材四年级下册第五单元“用画图策略解决问题”一课时，学生根据题意很快就通过画图解决了问题。

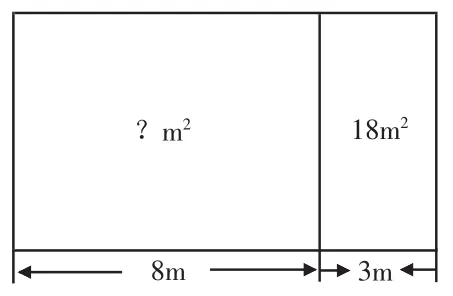
师（出示题目：校园里原来有一块长方形花圃，长为8米。在修建校园时，把花圃的长增加了3米，这样面积就增加了18平方米。原来花圃的面积是多少平方米？）：这道题目应该怎么做？

生1：长方形的面积等于长乘以宽。我想先画一个长方形，把题目中的已知条件标在这个长方形上，这样方便解题。

师：画图可以让题意更加直观清晰，方便我们寻找解题思路。大家试着画一画，再列式计算。

生2：我根据“花圃长增加3米，面积增加18平方米”这个条件计算出长方形的宽是18÷3=6（米）。这时长方形的长是8米，所以原来花圃的面积是8×6=48（平方米）。

师：回顾一下刚才的解题过程，想一想画图在解题过程中起了什么作用。

生3：画图可以清楚地看出数量之间的关系。

生4：通过画图可知道这道题目要先算出长方形的宽，再算长方形的面积。

生5：结合画图进行讲解可以更清楚地说出哪个长方形中的长或宽，大家听起来会更明白。如果没有图的话，有的人可能会听不明白。

在这个教学片段中，学生根据题意画示意图，可使题目中隐蔽的信息变得直观明了，同时将题目中的数量关系形象地表示出来，降低了理解的难度。教师要注意引导学生将线索清晰准确地表达在图上，力求化繁为简，使得在图画中就能展示清晰的思路和线索。

三、借助画图策略，渗透数形结合

“数形结合”是重要的数学思想方法之一，学生利用画图策略，可深刻体会到数形结合的优势是形象直观、便于理解。当然，每个年级的学生对画图策略和数形结合思想方法的理解也是不同的，低年级学生以“形象直观”为基础，中高年级学生“逐步抽象”是过程。

例如，在教学苏教版教材一年级第五单元“比多少”一课时，课始我以“三只猴子分水果”的情境引入，让学生说一说从图中获得了哪些数学信息。学生将看到的信息一一指出：三个桃子、四个梨、两个香蕉和三只猴子，随即我引导学生思考：你能提出哪些数学问题？在学生提出问题“三个桃子分给三只猴子，够分吗”后，我及时追问：“为什么你觉得桃子够分了？你是怎么想的？”随即让学生借助图片摆一摆、比一比、画一画，在比较和摆放过程中学生进行数形结合，从而得出桃子和猴子数量是一样的，都是3，引出等于符号和“3等于3”。“你还能提出类似的问题吗？同桌合作，一个提问，一个通过摆一摆来比较，注意在摆的时候要一个和一个对齐哦。”……

上述教学案例中，学生借助摆图直观、形象地理解在“一一对应”的前提下，比较哪个多哪个少的方法，为后续学习各类比大小的内容打好基础。

又如，在教学苏教版教材六年级下册“鸡兔同笼”一课时，我先出示“鸡兔同笼”的题目：笼子里有若干只鸡和兔，从上面数有8个头，从下面数有26只脚。鸡和兔各有多少只？我首先引导学生用圆片当作鸡或兔摆一摆，通过同桌合作边摆边画边说，引导学生用假设都是兔子或都是鸡的方法解题；然后让学生通过画图将头脑中初步建立的实物表象记录在学习单上，从实物图转变为抽象的个性图，提升学生的抽象数学思维；最后，让学生结合图形列出对应的算式，通过把画图与算式建立相应的关系，帮助学生形成数学思维。

上述教学，从摆一摆、画一画到算一算，学生经历从形象直观到抽象画图及算式归纳的过程，这种从形象到抽象的过程符合学生的认知发展，有效培养了学生的数学思维，同时让学生感受到数形结合思想方法的重要性。

四、借助画图策略，提高画图能力

培养学生的画图能力不是一蹴而就的，首先要让学生体会到画图的重要性，让画图成为学生解决问题的一种方式；其次，在比较和解决数学问题的过程中，让学生体会画图的简洁性，感受画图对解题的价值。

例如，我在教学苏教版教材一年级上册“期末复习”时，曾遇到一道较为棘手的“排队问题”，学生从最初的猜测到用实物画图，最后想到用简洁的数学符号来记录，这样的思考过程提高了学生的画图能力。

师（出示题目：小动物们在排队。从前往后数，第5只是小鹿；从后往前数，第8只是小鹿。一共有多少只小动物？）我们一起来读一读这道题目，边读边想，你能想出一幅图吗？你能猜一猜一共有多少只小动物吗？

生1：5+8=13（只）。

生2：5+8+1=14（只）。

生3：5+8-1=12（只）。

师：到底有多少只呢？你们有什么办法确定吗？

生4：可以把这些小动物画下来，然后数一数一共有多少只。

师：很棒的想法，大家用画图的方法来试一试吧！

生5：我画好了，数了一下，一共有12只小动物。

师：大家觉得每次都这样画小动物麻烦吗？（太麻烦了）能想个好办法吗？

生6：我们可以用圆形、三角形、正方形代替小动物。

在这个教学片段中，教师通过层层追问，引导学生想到用画图来解决“排队问题”，再想到利用画小动物来解决问题，最后想出用简洁的数学符号来解决问题。步步推进的教学设计，使学生的数学思维和画图能力得到了很好的培养。

总之，画图不仅可以用来解决数学问题，还可以用来梳理知识、对比算式和挖掘数量关系等。借助画图策略，学生可以验证算式的对与错，也可以通过算式反刍图的对与错，极大地促进了学生数学思维的提升。