以形助数，促进学生千以内数的数感培养

华东师范大学附属外国语实验学校（201100） 孔 妍

【活动背景】

数射线（千）这一内容在整个小学阶段的数的概念教学中起着承上启下的作用。关于这个内容，沪教版教材安排了比较多的练习，如字母表示数、数数、找相邻数、比大小，以及再加几就是1000等，都是借助数射线引导学生感知数与数之间的内在关系，从而建立数感，为理解运算做准备。数射线是学生在一年级就已经接触并且比较熟悉的工具，因此，要借助数射线进一步建立千以内数的数感，有两个难点：熟练运用数射线找数的策略；整体把握几个数的大小关系。为突破这些难点，我设计了在数射线上“确定整百数对应的点的位置”“找到374所对应的点的位置”“确定数的大概位置”等系列活动，试图通过这些活动帮助学生进一步建立千以内数的数感。

【活动描述及效果】

为了让学生快速进入学习状态，课前我特意安排了在数射线（百）上找数的练习，通过找数的复习，沟通数射线（百）和数射线（千）的知识，帮助学生将旧知迁移到新知。

活动一：在0到1000的数射线上确定整百数对应的点的位置

在这条数射线上，这样的一格表示多少？

300可能在什么位置？你是怎么想的？

我们都说大概在这，那真的在这里吗？怎样验证你的答案？

怎样平分这样的一格就能确定它的准确位置了？

学生根据已有的经验，会认为数射线上的单位长度是固定的，一格表示1。然而随着知识的增长，要想在数射线上表示更大的数必然要使单位长度发生变化。此活动设置在一条只有0和1000两个刻度的数射线上，让学生确定整百数300的准确位置，目的有二：一是让学生关注到单位长度可以不是1，有可能比1大，也可能比1小；二是在确定整百数的准确位置的过程中，使学生进一步细分单位长度，而细分的依据就是计数单位百和千的关系——10个百是1000，从而进一步感悟计数单位的产生和建立千以内数的数感，让学生初步感知找数的方法、单位长度的变化以及计数单位的产生。

学生的完成情况：

将0～1000平分成2格、4格、5格，指出300的大概位置

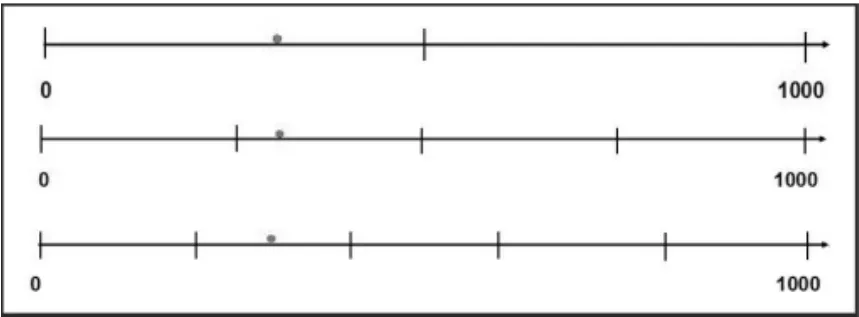
将0～1000平分成10格，每格表示100，从0开始往右数三格就是300。

对于找整百数，大部分学生是能感觉到300离0近，而离1000远的，也能指出大概的位置，但是和准确位置还是有一定差距。在活动中，教师要一步步引导学生感悟平分的策略，通过层层递进的追问，引导学生总结出平分的方法及依据。根据学生的活动情况，将活动效果分为两类：第一类是学生在教师和同学的启发下，尝试用平分解决问题，但是因为平分的格数所限，最终确定的位置仍是大概位置；第二类是学生根据计数单位间的进率，将0～1000平分成十格，能在数射线上找到与计算单位对应的位置，从而找到整百数300的准确位置。

活动二：找到374所对应的点的位置

370可能在什么位置？你是怎么想的？

怎样找到370的准确位置？先讨论，然后在学习单上记录想法。

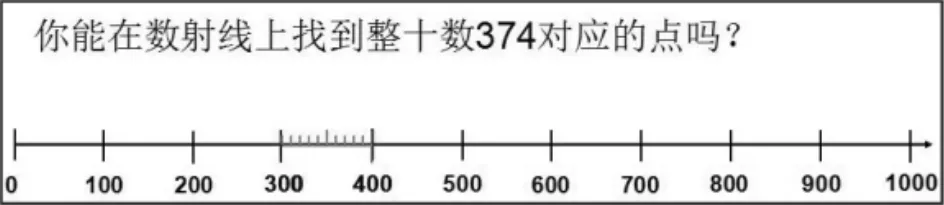
如果让你找374的位置？又该怎么操作？

此活动是对策略的进一步巩固和运用。通过找整十数和个位不为0的数，让学生在充分的尝试和体验中感悟单位长度的变化和计数单位间的进率大小。

学生的完成情况：

（1）370所对应的点的位置

300和400的中间是350，350靠右一点，400靠左一点就是370。

300和400之间平分5格，360和380的中间是370。

把300和400之间平分10格，这样每格表示10，从300开始数7格就是370。

此活动中，大部分学生能够先确定好370的范围在300和400之间，而以上的三种结论体现了学生的思维是层层深入的，学生能在互动中根据10个十是100，将单位长度进一步细分为10格，从而找到370的准确位置。

（2）374所对应的点的位置

先确定374的范围，在370和380之间，根据10个一是十，将370和380之间平分成10格，370向右4格就是374。

经历了活动一后，学生已经初步认识了平分的依据和方法，但是在方法的运用上还需教师进一步引导。第一个小活动“找整十数370”，部分学生还是想直接确定它的大概位置，但也有部分学生想到了平分，因此，这个环节采用生生互动的形式，让一部分学生启发另一部分学生，使得到了第二个小活动“找374”时，大部分学生很快就清楚要平分10格。

活动三：在0～1000的数射线上确定数的大概位置

刚才你们已经能够在数射线上精确地找数了，真棒！现在你能不能尝试估一估这些数宝宝的大概位置？先独立思考，然后同桌互相交流想法并记录下来。

通过之前的活动，学生已经掌握了如何确定千以内数的准确位置和在数射线上找到千以内的数，活动三是让学生经历在只有0和1000刻度的数射线上找数的过程，从而学会整体把握数的相对大小，建立数感。

学生的完成情况：

先确定500的大概位置，它在0和1000的中间。

对618的大概位置的两种不同想法。

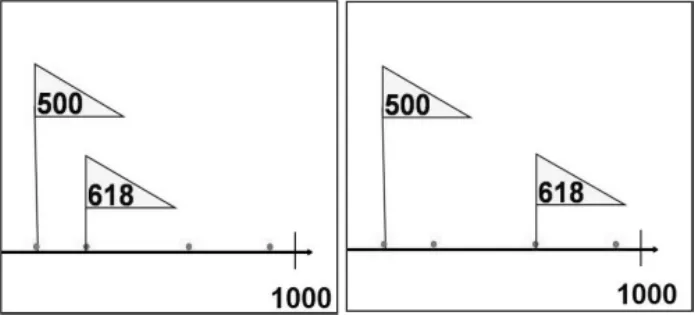
学生能根据“500是1000的一半”，很快确定了数宝宝500的大概位置。对于618的大概位置，部分学生只关注到了618的范围在500和1000之间，没有关注到618与500和1000的相差关系。在教师的引导下，学生认识到：在确定数宝宝618的大概位置时，先确定它的范围在500和1000之间，再根据“618和500相差小而和1000相差大”，选择靠近500的点。

对180和200的大概位置的三种不同想法：

确定180和200是这个活动的难点，干扰点的设置使得学生学会整体观察几个数的相对大小显得尤为重要。在活动中，学生意识到：180和200只相差20，200和500相差300，所以在这条数射线上，200离180很近，离500较远。

【活动反思】

1.发挥提问的调促作用，感悟策略的生成

在活动一中，当我提出第一个问题“300可能在什么位置？你是怎么想的？”时，大部分学生虽然能很快指出300的大概位置，但和准确位置还是存在一定的差距。我接着追问“一定在那里吗？”，目的是促使学生深入思考找到准确位置的方法，然而学生这时确定自己的猜测是正确的，并且没有要进一步思考的打算。显然，是跟进的问题不够明确，于是我进行了调整：“我们都说大概在这，那真的是这里吗？怎样验证你的答案？”这时，学生很自然地开始讨论验证的方法，大部分学生会想到先找到500，再找300，个别学生还想到了进一步平分。我继续追问：“怎样平分能确定它的准确位置？”然后引导学生针对“将0～1000平分成2格、4格和10格”集中讨论，进而总结出：根据10个百是1000，把0～1000平分10格就能找到整百数。

2.注重学生的学习体验，提升策略意识

找整百数、整十数和个位不为0的数的活动设计的目的是让学生在一步步细分数射线的过程中感悟计数单位的形成以及数范围的缩小过程，形成在数射线上找三位数的策略：先找相邻的整百数，再找相邻的整十数，最后精确到个位。在教学中，如果三个环节都是采用相同的模式进行，就会出现个别替代整体的问答形式，无法保证全班学生的共同参与。如果大部分学生没有经历策略的运用过程，策略意识又何从谈起？因此，我及时改变了活动的设计方案，在层层递进中提升策略意识：层次一，在找整百数过程中渗透平分策略，让学生感悟策略的生成；层次二，学生讨论并尝试找整十数，进一步感悟平分策略并学会运用；层次三，学生独立解决“找个位不为0的数”的问题，深化平分策略的认识和运用。

3.关注学生的思维表达，促成“推理有据”

对于确定数的大概位置，很多学生是有感觉的，然而仅仅是感觉，因此，适时的说理训练很有必要。说理无非是从这几点展开：怎么做？为什么这样做？是什么促使你这样做？在活动三的实施过程中，针对学生的表达基础，面对学生呈现的资源，我提出问题：“在说出答案前你能否给大家一些启发？你是怎么想的？为什么这个数宝宝会在这里？你的依据是什么？”一是根据学生的差异提出分层次的要求，二是引导学生通过对一系列问题的思考，养成推理有据的习惯。