函数在不等式 证明中的应用

（云南省西双版纳傣族自治州民族中学 云南西双版纳 666100）

高中数学是学生在整个高中学习中的重点科目也是难点科目，在实际的教学过程中，函数的运用又是学生的一大难点，这要求学生对于函数知识要有非常深刻的理解，以及在利用函数证明不等式中的深层联系也有较高的要求。

一、利用函数解决不等式的证明问题

1.利用函数的单调性证明不等式问题

利用函数的单调性来证明不等式问题是一种常见的也是很有用的方法，运用函数单调性时，要有明确的定义域区间要求，函数的单调性是基于函数的区间来确定的，即函数在某一区间是增函数，可能在其他的区间就是减函数。因此，利用单调性证明函数的单调性问题时，首先要确定函数的定义域区间。

下面以2017年江苏高考数学题第20题前两问为例：

例1：已知函数f(x)=x3+ax2+bx+1（a＞0，b∈R）有极值，且导函数f′(x)的极值点是f(x)的零点，（极值点是指函数取极值时对应的自变量的值）

（1）求b关于a的函数关系式，并写出定义域；

（2）证明b2＞3a；

证明：（1）由，得

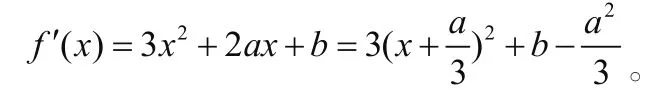
当时，f′(x)有极小值

因为f ′(x)的极值点是f(x)的零点。

所以

又a＞0，故

因为f(x)有极值，故f′(x)=0有实根，

从而，即a≥3。

a= 3 时，f′(x)＞0(x≠-1)，故f(x)在R上是增函数，f(x)没有极值；

a＞3时，f′(x)=0有两个相异的实根

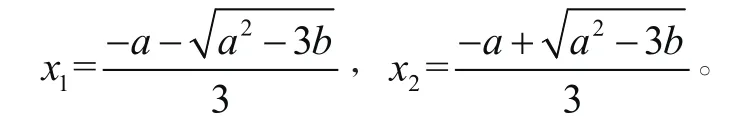
根据其极值与单调性判断得：f(x)的极值点是x1x2。

从而a＞3，因此，定义域为(3,+∞)=。

（2）由第一问可知，

那么设，则

当时，g′(t)＞0，从而g (t)在上单调递增。

因为a＞3，所以，故，即。因此2＞3ba。

从以上的例子可以看出，在利用单调性证明不等式问题时，首先要明确不等式成立的定义域区间，其次，就是设立合适的函数了。以上的例子中，根据题意直接构建新的函数，对这个函数求导，然后研究它的单调性，从而判断出所证不等式的大小关系。

2.利用函数的最值证明不等式

利用函数的最值来证明不等式也是一种常用的方法。函数的最值也是建立在一定的区间上的，定义域的区间不同，那么在这一段区间上函数的最值也有可能不一样。利用函数的最值，即先根据定义域求出不等号两边的函数最值，然后将两个最值相比，自然而然的就求证出了不等式的问题。

下面再以2017年全国新课标卷文科数学第21题为例

例2：已知函数f(x)=ex（ex-a）-a2x.

（1）讨论f(x)的单调性；（2）若f(x)≥0，求a的取值范围。

证明：（1）函数f(x)的定义域为(-∞, +∞),

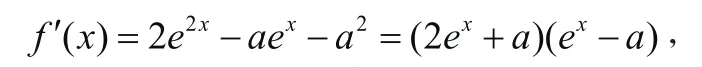
①若a=0 ，则f(x) =e2x，在(-∞,+∞ )单调递增。

②若a＞0，则由f′(x)=0得x=lna。

当x∈(-∞,lna)时，f′(x)＜0；当x∈(lna,+∞)时，f′(x)＞0，所以f(x)在(-∞,lna)单调递减，在(lna,+∞)单调递增。

③若a＜0，则由f′(x)=0得

当时，f′(x)＜0；时，f′(x)＞0，故f(x)在

当单调递减，在单调递增。

（2）在第一问得知函数的单调性情况下，分情况讨论

①若a= 0 ，则f(x)=e2x，所以f(x) ≥0。

②若a＞0 ，则由（1）得，当x=l na时，f(x)取得最小值，最小值为 f(lna )=-a2lna。从而当且仅当-a2ln a≥0，即a≤1时，f(x)≥0 。

③若a＜0，则由（1）得，当时f(x)取得最小值，最小值为

从而当且仅当，即时f(x) ≥ 0 。

综上，a的取值范围为

此题中，根据实际情况的需要，对a的取值范围进行讨论，求出不同情况下函数的最值，从而顺利的证明不等式。

结语

函数问题是贯穿于整个高中数学的最为重要的问题，并且在学生的大学时代还有更加深层次的研究，同时，函数对于其他学科的研究有着重大的作用。在利用函数时，可以利用函数的单调性、最值等方法，快速有效的解决不等式的证明问题，同时，要特别关注函数的定义域问题，避免出现不同定义域而导致的函数应用错误，或者不等式证明错误等问题。因此，教师们在平时的教学过程中，应该加强学生这一方面的教学，引导学生自己理解、并总结相关的不等式证明的方法，并多多加以练习。长此以往，学生对于这一方面问题的解答，定会有突飞猛进的提高。

[1]华东师范大学数学系编,数学分析上册[M].北京：高等教育出版社,2001,119-156.

[2]尚肖飞,贾计荣.利用导数证明不等式的若干方法[J].太原教育学院报,2002,20（02）：35-37.