一类Helmholtz方程解的存在性和唯一性
2018-06-04赵远英
管 毅, 杨 媛, 赵远英
(贵阳学院 数学与信息科学学院, 贵州 贵阳 550005)
1 引言及预备知识
在声波的散射问题中,裂缝散射较为常见.许多专家学者深入研究了裂缝散射问题[1-5].近年来,一些学者转向带裂缝的较为复杂的散射体的散射问题,Kirsch等[6]利用积分算子的方法研究了带Neumann边界条件的裂缝散射问题;Kress等[7]将裂缝散射问题推广到第三类边界条件;Cakoni等[8]考虑了一条裂缝具有不同边界条件的散射问题.
Krutitskii[9]利用积分算子的理论研究了平面上一条裂缝散射问题,Yan[10]考虑了平面内由两部分组成的一条光滑裂缝散射问题,其中散射波在裂缝的2个不同部分具有不同的边界条件.Yan[10]利用位势理论和边界积分方程中的积分算子性质,通过Fredholm定理,得到该问题解的存在性和唯一性.Guo等[11]研究了裂缝散射问题解的性态以及相应的数值解法,李妮等[12]研究了不可穿透物体外带一条可穿透裂缝的散射问题,其中散射波在不可穿透障碍物边界上满足第一类边界条件,在裂缝两边分别满足第一、第三类边界条件.
本文主要考虑的也是一个不可穿透障碍物外加一条裂缝所组成的散射体散射问题.不同于前面的研究,本文涉及的不可穿透障碍物由两部分组成,分别满足不同的边界条件,通过位势理论和积分算子知识,得出此类边值问题的解的存在性和唯一性.
2 边界积分方程组
考虑平面上一个不可穿透障碍物外加一条可穿透裂缝的散射问题.障碍物边界由两部分组成,∂D=S1∪S2,两部分边界上满足不同的边界条件.假设障碍物D外的裂缝Γ是平面某光滑闭曲线∂Ω的一部分,这样Γ上的外法线方向n与∂Ω上的外法线方向一致.
U-=0,x∈Γ,
U=0,x∈S1,
(1)
其中,U是总场,U=ui+us,ui=eiks·d,d为入射方向,且要求散射波us满足Sommerfeld辐射条件.
如果只考虑散射场,则只考虑如下方程
U-=p(x),x∈Γ,
U=f(x),x∈S1,
(2)
给定

(3)
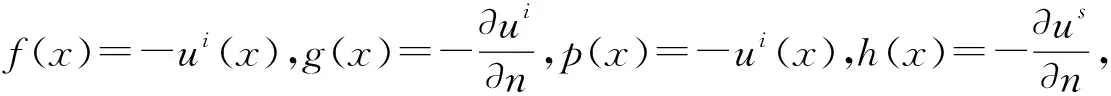
定理2.1方程(2)和(3)至多有一个解.

在区域BR
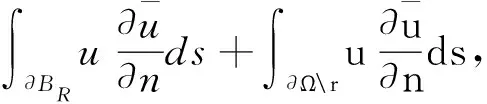
(4)
在区域Ω
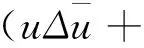

(5)
故有

从而有
引理2.1如果u是方程(2)和(3)的解,则有
证明参见文献[13].
下面通过格林公式寻找方程的解.




故原方程的解可表示为

(6)

考虑边界∂D=S1∪S2的情形.

从而有

(7)
将上式限制在边界S1上,根据已知条件有
其中算子S、K、K′和T均为相应的边界积分算子,定义如下:
故有
算子SDS1表示在前面定义的算子S中,密度函数定义取值在边界∂D上,然后将最后的积分值限定在边界S1上.应用格林公式和辐射条件,有如下结论(见文献[14]).
引理2.2
x∈∂D, y∈∂Ω,
f(x)=SS1S1γ1+SS2S1g-KS1S1f-KS2S1γ2+
SΓS1α-KΓS1β,
故有
SS1S1γ1-KS2S1γ2+SΓS1α-

(8)
其中
从上分析知
(9)
将x限定在边界S1上有
故有
(10)
其中
再看边界Γ上的情形.


(11)

(12)

(13)
以及
(14)
将自变量限定在边界Γ上有
即有
u-|Γ=SS1Γγ1+SS2Γg-KS1Γf-KS2Γγ2+
故
u+|Γ=[u]|Γ-u-|Γ,
故有
u-|Γ=SS1Γγ1+SS2Γg-KS1Γf-KS2Γγ2+
SΓΓα-KΓΓβ+[u]|Γ-u-|Γ,
整理得
SS1Γγ1-KS2Γγ2+SΓΓα-

(15)
其中
从而有
故有

(16)
其中
联合(8)、(10)、(15)和(16)式,有如下方程组
Aξ=η,
(17)
其中
向量η为

算子A为
3 解的存在性和唯一性
显然,若从上述方程组中求解出未知量ξ,则原方程就有解存在.利用Fredholm定理,有如下结论.
定理3.1积分方程组(17)解存在且唯一.
证明下面分两步证明该结论.
第一步,证明算子A是具有零指标的Fredholm算子;第二步,证明算子A是单射.
现在证明第一步:由参考文献[14]知,对于算子S和T,分别存在紧算子Cs和CT,其中
分别满足:



而
对于
ξ=(γ1,γ2,α,β)T,
H
其对偶空间H*改写(17)式为
其中
且


(18)
其中()表示相应的边界上的L2内积.
Re(-(KS2S1γ2,γ1)+(γ1,KS2S1γ2))=

(19)
同理
Re((β,α)-(α,β))=


从而有
故可以说明算子A是具有零指标的Fredholm算子.
下面证明第二步,说明A是单射.
设ξ=(γ1,γ2,α,β)T满足齐次方程Aξ=0,即等价于如下方程组
下面证明ξ=(γ1,γ2,α,β)T=0.定义位势函数


SΓS1β-KΓS1β),
根据(20)式的第1个方程有
v(x)|S1=0.

根据(20)式的第2个方程有

SΓΓα-KΓΓβ+β),
根据(20)式的第3个方程有
v(x)|Γ=0.
4) 当x∈R2Ω,x→Γ时有
根据(20)式的第4个方程有
综上所述,v(x)满足如下边值问题
(21)
和辐射条件方程
(22)
[1] AMMARI H, GANG B, WOOD A W. An integral equation method for the electromagnetic scattering from cavitys[J]. Math Meth Appl Sci,2000,23(12):1057-1072.
[2] CHENG J, HON C, YAMAMOTO M. Conditional stability estimations for a inverse boundary with non-smooth boundary inR3[J]. Trans Am Math Soc,2001,353:4123-4138.
[3] COLTON D, KRESS R. Inverse Acoustic and Electromagnetic Scattering Theory[M]. Berlin:Springer-Verlag,1998.
[4] COLTON D, KRESS R. Integral Equation Methods in Scattering Theory[M]. New York:Springer-Verlag,1983.
[5] COSTABEL M. Boundary integral operator on Lipschitz domains:elementary results[J]. SIAM J Math Anal,1988,19(3):613-626.
[6] KIRSCH A, RITTER S. A linear sampling method for inverse scattering from an open arc[J]. Inverse Problem,2000,16(1):89-105.
[7] KRESS R, LEE K M. Integral equation method for scattering from and Impedance crack[J]. Comput Appl Math,2003,161(1):161-177.
[8] CAKONI F, COLTON D. The linear sampling method for cracks[J]. Inverse Problems,2003,19(2):279-295.
[9] KRUTITSKII P A. The Helmholtz equation in the exterior of slits in a plane with different impedence boundary conditions on opposite slides of the slits[J]. Quart Appl Math,2008,67(1):73-92.
[10] YAN G Z. Boundary integral methods for scattering problem with cracks buried in a piecewise homogeneous medium[J]. Math Meth Appl Sci,2011,35(1):84-96.
[11] GUO J, FAN L L, YAN G Z. The boundary integral method for the Helmholtz equation with cracks inside a bounded domain[J]. Acta Mathematica Scientia,2015,B35(3):539-551.
[12] 李妮,王连堂. 混合边界下开弧外区域声波散射问题的数值解法[J]. 纯粹数学与应用数学,2015,31(2):164-170.
[13] 严国政. 具有混合裂缝散射问题的边界积分方程方法[J]. 数学物理学报,2011,A31(5):1167-1175.
[14] 毛耀. 复杂散射体声波正散射和逆散射问题的研究[D]. 武汉:华中师范大学,2012.
[15] KRESS R. Linear Integral Equation[M]. 2ed. Berlin:Spring-Verlag Press,1999.
