交互作用Fock空间l2(Γ)上的湮灭算子和增生算子

周玉兰, 赵丹丹

(西北师范大学 数学与统计学院, 甘肃 兰州 730070)

在20世纪90年代,由于量子概率的发展,出现了一种描述粒子系统的新结构——交互作用Fock空间[1].交互作用Fock空间来源于量子电动力学的随机极限,文献[2]给出了其公理化的定义,它主要应用于交互量子领域、中心极限定理和非交换概率[3-8]研究.

设K=L2(X,μ)是复Hilbert空间,记

则称Γ(K)为有关交互因子{λn}n∈N的交互作用Fock空间，其中Kn是K⊗n关于内积

〈Fn,Gn〉n=

的完备化,即Kn为n-粒子空间[9].由于粒子可能增生或者湮灭,而在一个系统中粒子总数是固定不变的,因此用增生算子和湮灭算子来描述粒子可能出现的情况.在文献[10-11]中,Wang等研究了量子Bernoulli泛函空间L2(Ω),即

其中

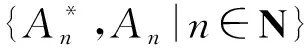
1 预备知识

定义1[9]设K=L2(X,μ)是复Hilbert空间,对于任意n∈N,K⊗n表示K的n次张量积,则K⊗n也是一维的,λn是Xn上的n元函数,在K⊗n上引入内积

〈Fn,Gn〉n=

Fn,Gn∈K⊗n.

K⊗n关于上述内积的完备化记为Kn,则称

为交互作用Fock空间,其中〈·,·〉n是n-粒子空间的内积,且{λn}n∈N满足条件

λn(xn,…,x1)=0⟹λn+1(x0,xn,…,x1)=0.

注1[9]1) 若对于任意n∈N,λn不是常数,则该空间称为一般交互作用Fock空间.

2) 若对于任意n∈N,λn是常数,则该空间称为单模交互作用Fock空间.特别地,若λn=1,则该空间称为自由Fock空间或者完全Fock空间.

定义2对于任意n≥1,任意f∈K,任意F∈Kn,A*(f)F=f⊗F∈Kn+1,Φ表示真空向量,即

Φ=1⊕0⊕0⊕…,

A*(f)Φ=f,

称A*为在f处的增生算子.

对于任意n≥1,任意G∈Kn,g∈K,

A-(g)G(x0,xn-1,…,x1)=

A-(g)Φ=0,

称A-为在g处的湮灭算子.

引理1[12]设(M,μ)和(N,ν)为测度空间,且L2(M,μ)和L2(N,ν)可分,则:

1) 存在唯一同构关系

L2(M,μ)⊗L2(N,ν)≅L2(M×N,μ×ν),

使得f⊗g对应于f(x)g(y);

2) 对任意可分Hilbert空间K,存在唯一同构关系

L2(M,μ)⊗K≅L2(M;K),

使得f⊗h对应于f(x)h.

引理2[12]设H1和H2为2个Hilbert空间,若{ej}j∈N和{fk}k∈N分别为H1和H2的正交基,则{ej⊗fk}j,k∈N为H1⊗H2的正交基.

接下来,定义基于l2(N)的交互作用Fock空间l2(Γ).它是一个非单模交互作用Fock空间,但它与单模交互作用Fock空间非常接近,其特殊性体现在交互因子{λn}n∈N上.

设Γ是自然数集N的有限幂集,记

Γ(n)={σ|σ⊆N,(σ)=n},

l2(N)是实值平方可和函数所构成的Hilbert空间,对任意f,g∈l2(N),其内积为

集合{f⊗n|f∈l2(N)}关于内积

〈f⊗n,g⊗n〉n=

f(xn)g(xn)λn(x1,x2,…,xn)

的完备化构成Hilbert空间,记为l2(Γ(n)),其上范数记为‖·‖n,其中

λ0=1,

λn(x1,x2,…,xn)=

定义3设{l2(Γ(n)),〈·,·〉n},n=0,1,2,…为上述Hilbert空间,记

在l2(Γ)中引入内积

∀F={fn},G={gn},

fn,gn∈l2(Γ(n)),

l2(Γ)为关于该内积的完备化Hilbert空间,称为关于交互因子{λn}n∈N的交互作用Fock空间.这里约定l2(Γ(0))=R.

对任意n∈N,任取σ∈Γ(n),记

δσ=

Sn(δa1⊗δa2⊗…⊗δan)=

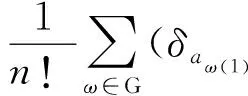
则

δσ∈l2(Γ),

其中,δai∈l2(N),ai∈N,i=1,2,…,n,G为{1,2,…,n}的n阶置换群.

命题1集合{1,δσ|σ∈Γ}为l2(Γ)的正交基.

证明由{δa|a∈N}为l2(N)的标准正交基及引理2易得.

根据定义2,在l2(Γ)上可定义一列点态增生和湮灭算子.

定义4任取

F={fm}∈l2(Γ),

对任意n∈N,有

AnF=

(0,…,1{x1,…,xm}(x)〈δn,f〉f⊗(m-1),…),

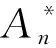
Anδσ(τ)=(1-1τ(n))δσ(τ∪n),

当n∉τ时有

Anδσ(τ)=δσ(τ∪n)=
δn(n)·δvaluen)(τ)=δvaluen)(τ)

;

而当n∈τ时,Anδσ(τ)=0,即

Anδσ(τ)=(1-1τ(n))δvaluen)(τ),

又

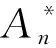
2 主要结果

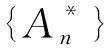
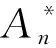
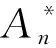
任取F={fm}m≥0,对任意n∈N,有

f2(xm-1)λm-1(x1,…,xm-1)≤

‖F‖2<+∞,

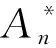
特别地,取F=(0,δn,0,…)∈l2(Γ),则

‖(0,1{x1}(x)〈δn,δn〉,0,…)‖2=1.

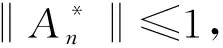
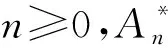
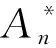
∀F,G∈l2(Γ).

证明任取F={fm}m≥0,G={gm}m≥0.对于任意n∈N,有

〈AnF,G〉=

(g0,g1,…,gm+1,…)〉=

f(xm)g(xm)g(n)λm(x1,…,xm),

其中,xi≠n,i=1,2,…,m;

〈(f0,f1,…,fm,…),(0,…,1{x1,…,xm}(y)×

〈δn,g〉g⊗m,…)〉=

f(xm)g(xm)g(n)λm(x1,…,xm),

其中,xi≠n,i=1,2,…,m.因此

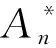
由文献[13],并结合定理1和定理2,可以得到推论1.

推论1任意n∈N,湮灭算子An为l2(Γ)上的有界线性算子,且‖An‖=1.

在一般交互作用Fock空间中,即使是单模交互作用Fock空间,增生算子和湮灭算子也只有不同态的交换关系,即

下面定理3表明:在l2(Γ)上所定义的这一列增生算子和湮灭算子,除了点态不同时具有交换关系外,在点态相同时还具有反交换关系.

定理3设k、l∈N,则

且

其中I是在l2(Γ)中的恒等算子.

证明对任意F={fn}∈l2(Γ),其中fn=f⊗n,f∈l2(N),n=0,1,2,…,对任意k、l∈N,

AkAl(F)=Ak(Al(…,f⊗n,…))=

(…,(1-1{x1,…,xn}(x))(1-

(…,(1-1{x1,…,xn}(y))(1-

Al(Ak(…,f⊗n,…))=AlAk(F).

由于{F={f⊗n},∀f∈l2(N)}是l2(Γ)中的稠密子集,又Ak、Al是l2(Γ)上的有界线性算子,从而Ak、Al可交换,即

AkAl=AlAk，

(…,1{x1,…,xn}(x)1{x1,…,xn}(y)〈δl,f〉×

〈δk,f〉f⊗(n-2),…)=

(…,1{x1,…,xn}(y)1{x1,…,xn}(x)〈δk,f〉×

〈δl,f〉f⊗(n-2),…)=

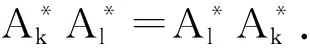
(…,(1-1{x1,…,xn}(x))1{x1,…,xn}(y)〈δl,f〉×

Ak(…,1{x1,…,xn}(y)〈δl,f〉f⊗(n-1),…)=

(…,1{x1,…,xn}(y)(1-1{x1,…,xn}(x))〈δl,f〉×

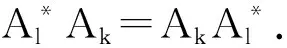
AkAk(F)=Ak(Ak(…,f⊗n,…))=

(…,0,…)=0,

(…,0,…)=0,

Ak(…,1{x1,…,xn}(x)〈δk,f〉f⊗(n-1),…)=

(…,(1-1{x1,…,xn}(x))〈δk,δk〉f⊗n,…)+

(…,(1-1{x1,…,xn}(x))f⊗n,…)+

(…,(1-1{x1,…,xn}(x))f⊗n,…)+

(…,(1-1{x1,…,xn}(x))f⊗n,…)+

(…,1{x1,…,xn}(x)f⊗n,…)=

(…,f⊗n,…)=I(…,f⊗n,…),

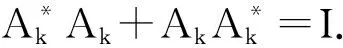
[1] ACCARDI L, LU Y G. The Wigner semi-circle law in quantum electrodynamics[J]. Communications in Mathematical Physics,1996,180(3):605-632.

[2] ACCARDI L, LU Y G, VOLOVICH I. The QED Hilbert module and interacting Fock spaces[DB/OL]. [2016-08-10]. http://www.researchgate.net/publication/282284148,1997-01.

[3] XU Q H. Remarks on interacting Fock spaces[J]. Infinite Dimensional Ayalysis, Quantum Probability and Related Topics,2000,3(1):191-198.

[4] ASAI N. Analytic characterization of one-mode interacting Fock space[J]. Infinite Dimensional Analysis, Quantum Probability and Related Topics,2001,4(3):409-415.

[5] ACCARDI L, KUO H H, STAN A. Characterization of probability measures through the canonically associated interacting Fock spaces[J]. Infinite Dimensional Ayalysis, Quantum Probability and Related Topics,2004,7(4):485-505.

[6] CRISMALE V. Quantum stochastic calculus on interacting Fock spaces:semimartingale estimates and stochastic integral[J]. Communications on Stochastic Analysis,2007,1(2):321-341.

[7] ACCARDI L, KUO H H, STAN A. An interacting Fock space characterization of probability measures[J]. Communications on Stochastic Analysis,2009,3(1):85-99.

[9] KANG Y B, WANG C S. Quantum stochastic integral representations on interacting Fock space[J]. J Theoretical Probability,2015,28(3):1007-1027.

[10] WANG C S, CHAI H F, LU Y C. Discrete-time quantum Bernoulli noises[J]. J Mathematical Physics,2010,51(5):23.

[11] WANG C S, LU Y C, CHAI H F. An alternative approach to Privault’s discrete-time chaotic calculus[J]. J Math Anal Appl,2011,373(2):643-654.

[12] 黄志远,王才士,让光林. 量子白噪声分析[M]. 武汉:湖北科学技术出版社,2004:13-30.

[13] 程其襄,张奠宙,魏国强,等. 实变函数与泛函分析基础[M]. 3版. 北京:高等教育出版社,2010:260-261.