非线性能量阱对飞轮振动抑制效果的实验研究
2018-06-04刘海平王耀兵孙鹏飞罗婕殷新喆
刘海平,王耀兵,孙鹏飞,罗婕,殷新喆
(1. 北京空间飞行器总体设计部,北京100094;2. 空间智能机器人系统技术与应用北京市重点实验室,北京100094)
0 引 言
在轨航天器振动源主要由姿态控制执行机构和驱动机构组成。其中飞轮和控制力矩陀螺工作时产生的振动是影响有效载荷工作性能的主要干扰源之一[1-4]。为便于指导飞轮振动抑制系统设计,众多学者研究了飞轮振动产生机制和机理。针对单个飞轮、飞轮和安装结构、多个飞轮等不同研究对象开展了理论分析和实验研究。
目前,针对星上飞轮系统已进行了大量的振动抑制研究[5-10]。徐超等[6]提出将阻尼层嵌入飞轮复合材料支架内提高系统阻尼比,进而实现飞轮扰振抑制;张庆君等[7]系统全面的梳理了光学遥感卫星微振动抑制设计方法和关键技术,并提出一种同时满足主动段和在轨段扰振抑制的隔振器设计方案;关新等[8]为兼顾高频和低频减隔振要求,提出采用被动元件实现类似主动隔振的控制规律,有效兼顾高频隔振和共振峰抑制的目标。由于飞轮旋转速度与含陀螺效应转子固有频率耦合共振放大引起了低频干扰。此类响应频率位于已有隔振系统的转折频率附近,仅通过阻尼抑振和线性被动隔振效果欠佳。为了克服以上问题,可实现靶能量传递的非线性吸振器(又称为非线性能量阱,NES)成为可行的技术途径之一。靶能量传递是一种可实现能量由振源向强非线性耦合的受体单向不可逆的完全传递。前期,本文作者[9-10]引入非线性能量阱的概念,利用薄片金属梁构建了多种非线性能量阱。在此基础上,通过动力学仿真分析,针对非线性能量阱控制不同工作状态下飞轮扰振的有效性进行了参数化研究。相比于常规的线性吸振器,非线性能量阱具备工作频带宽、吸振效率高、鲁棒性强、可靠性高、不需要提供额外能量、附加质量小等优点。
为了验证非线性能量阱对飞轮振动特性的抑制效果,搭建了地面模拟飞轮测试系统(简称飞轮测试系统)并对安装非线性能量阱前后,在不同载荷条件下系统的动态响应特性进行对比评估。利用实测数据,采用傅里叶变换方法将测试系统内各典型位置的动态响应信息分别在时间域和频率域内展开。
1 实验介绍
1.1 飞轮测试系统
为了验证非线性能量阱对飞轮系统振动特性的抑制效果,设计并制作了1套飞轮测试系统如图1所示。该系统主要包括:模拟飞轮、触摸式控制模块、柔性支架等部分。其中,飞轮最高转速5000 r/min,速度控制误差小于0.1%,可实现恒加减速,升降速运行,含多片偏心弧片和圆环片,可改变模拟飞轮质心位置。控制模块使用ASDA-Soft软件具备示波及实时数据存储功能,有触摸屏可实现人机交互操作。柔性支架采用截面规格为20 mm×20 mm×1.2 mm方形铝管焊接而成,为设备和模拟飞轮提供安装面。测试系统总质量约为6.4 kg(不含控制模块)。
1.2 非线性能量阱设计
首先,对非线性能量阱的几何参数进行设计。根据文献[9-11]中提出的方法,采用金属薄片梁作为非线性刚度元件,两端固定在柔性支架侧面,薄片梁中部采用钢制螺栓和螺母连接,该组合体作为吸振子如图2所示。
对飞轮测试系统和非线性能量阱建立系统动力学方程。将飞轮测试系统沿水平方向简化为三自由系统,非线性能量阱表示为非线性弹簧和集中质量如图3所示。
由图3可见,利用有限元方法可等效得到飞轮测试系统各部分的等效质量mi、等效阻尼系数ci和等效刚度系数ki(i=1,2,3);非线性能量阱则表示为集中质量mNES,阻尼系数cNES和非线性刚度系数kNES。其中,非线性刚度系数kNES主要考虑线性刚度项kN1和立方刚度项kN3的影响。飞轮测试系统各部分等效质量的位移和非线性能量阱的位移分别表示为yi(i=1,2,3)和yNES。
建立飞轮测试系统和非线性能量阱的系统动力学方程:
kN3(yNES-y3)3=0
(1)
kN1(y3-yNES)+kN3(y3-yNES)3=0
(2)
k3(y2-y3)=0
(3)
(4)
利用以上所建动力学方程,可对由金属薄片梁构成的非线性能量阱进行理论分析和参数化设计[9-11]。基于小变形假设,根据能量定理建立了受载变形薄片梁的表征模型。为了评估不同设计参数对非线性能量阱振动控制效果的影响,从能量角度定义非线性能量阱瞬时能量比和非线性能量阱瞬时耗能比,确定设计参数最优值。通过参数化研究给出非线性能量阱的初始阈值特征和靶能量传递特征。在此基础上,选择金属薄片梁规格为100 mm×20 mm×0.15 mm,钢制螺栓和螺母构成的吸振子质量约为0.02 kg。与测试系统总质量相比,非线性能量阱质量仅为其总质量的0.3%。
1.3 实验工况
为了便于研究非线性能量阱对飞轮系统振动特性的抑制效果,分别对安装非线性能量阱前后飞轮系统的响应特性进行测试。为考核不同类型载荷作用下的振动控制效果,选择力锤敲击和飞轮以2000 r/min恒定转速稳定运行时的两种工况。其中,使用力锤敲击柔性支架侧面施加冲击载荷;保持飞轮以恒定转速2000 r/min运转,获得其稳态运行条件下的宽频线谱扰动载荷。在不同载荷激励条件下,分别采集安装非线性能量阱前后柔性支架不同位置点的振动响应进行对比。
分别选择四个测点,测点#1位于设备安装面,测点#2位于力锤敲击位置附近,测点#3位于飞轮安装面,测点#4位于非线性能量阱吸振子附近,参见图1和图2。
加速度传感器选用PCB 356B11,力锤选用Kistler 9722A2000。
2 冲击载荷工况
2.1 柔性支架加速度时程响应
使用力锤敲击柔性支架侧面施加冲击载荷,在安装非线性能量阱前后柔性支架上设备安装面(测点#1)的加速度时程响应如图4所示。
针对峰值为30 N的冲击载荷,初始加速度峰值未发生明显变化;冲击载荷峰值增加到240 N时,则初始加速度峰值由10.3g减小为7.6g,衰减量约为26.2%。在整个时程范围内,安装非线性能量阱以后,虽然对最大加速度峰值控制效果明显,但是由于吸振子质量和阻尼较小,所以结构振动响应衰减缓慢。
2.2 NES加速度时程响应
不同量级冲击载荷作用下,非线性能量阱发生显著的振动响应参见图5。
在分析时程范围内,小量级(30 N)激励下,非线性能量阱的响应全时段显著大于柔性支架设备安装面;载荷量级增至240 N,在0 s~0.04 s内,非线性能量阱振动响应显著大于柔性支架设备安装面;随着支架响应的减小,在0.04 s以上时段,非线性能量阱和支架的响应迅速减小。出现这一现象的原因在于,大量级输入载荷可以激发非线性能量阱的定向能量传输;随着能量耗散,输入非线性能量阱的能量减小,其抑振效果减弱。
对比图5(a)和图5(b)可见,大量级载荷激励下,非线性能量阱的抑振效果更好。
2.3 频域响应
为了分析非线性能量阱的宽频振动抑制效果,对不同量级冲击载荷作用下的加速度响应进行傅里叶变换,在频率域展开对其进行对比研究。
图6给出冲击载荷作用下,安装非线性能量阱前后的设备安装面的加速度频谱,以及非线性能量阱吸振子的加速度频谱。对比可见,非线性能量阱主要削弱其在冲击载荷作用下的第一个响应峰,对其他频点峰值的影响较小。其中,冲击载荷峰值为30 N时,设备安装面加速度频谱未发生明显减小。冲击载荷峰值为240 N时,设备安装面加速度频谱由0.031g减小为0.02g,衰减量约为35.5%;在其他频点的加速度响应峰值也均有不同程度减小。
观察非线性能量阱的加速度频谱,除了与柔性支架相互作用,在设备安装面第一个响应峰处发生显著振动响应之外,在0 Hz~800 Hz频段内出现多个宽频的加速度响应峰。除此之外,对比图6(a)和图6(b),随着输入冲击载荷增加,非线性能量阱分布在200 Hz~800 Hz频段内加速度响应峰值和数量均有增加。这一现象充分证明非线性能量阱可实现宽频振动抑制的非线性特征。从能量的角度,输入能量一定的条件下,将单频点或者有限频点的振
动响应采用非线性手段分布到较宽频率范围内,在系统振动能量不变的条件下相应各频点的绝对响应将得到显著削弱。
3 模拟飞轮开机工况
飞轮系统在稳定运行过程中,受到其动静不平衡、电磁噪声,飞轮与柔性安装结构耦合作用等因素影响产生宽频线谱扰动。为了评估非线性能量阱对飞轮系统输出线谱激励的抑制作用,实测飞轮以恒定转速2000 r/min运行时,安装非线性能量阱前后系统的响应特性。
3.1 飞轮安装面加速度时程响应
图7给出飞轮以2000 r/min恒定转速运行过程中,飞轮安装面的加速度时程响应曲线,采样时间长度为16 s。为了便于观察,截取0 s~0.03 s时间段内时程曲线如图7(b)所示。由图可见,安装非线性能量阱前后,响应曲线均出现明显的调制现象,且安装非线性能量阱前响应曲线幅值略大。由此说明,非线性能量阱有效。
3.2 设备安装面加速度时程响应
飞轮以恒定转速2000 r/min运行过程中,设备安装面的加速度时程响应曲线如图8所示。与飞轮安装面变化规律相似参见图7,安装非线性能量阱后加速度响应略小,且安装前后响应曲线存在相位差。此外,受飞轮输出扰动的影响,响应曲线呈现明显的调制特征。
3.3 NES加速度时程响应
与第3.1节和第3.2节相同工况下,非线性能量阱吸振子和飞轮安装面的加速度时程曲线如图9所示。
由图9(a)可见,飞轮安装面加速度响应幅值均大于非线性能量阱吸振子的响应。与冲击载荷作用下非线性能量阱吸振子响应大于柔性支架其他位置响应结果相比,原因在于冲击载荷属于瞬态激励,在短时间激励后再无能量输入测试系统;然而,飞轮以恒定转速运行稳态激励能量不断输入测试系统。因此,导致非线性能量阱吸振子响应特性发生变化。
将非线性能量阱吸振子和飞轮安装面的加速度时程曲线局部放大参见图9(b)。可见,飞轮安装面和非线性能量阱吸振子加速度响应曲线呈现出强调制特征,且存在相位差。
3.4 频域响应
为分析在稳态载荷激励下,非线性能量阱宽频振动抑制特性,对飞轮安装面和非线性能量阱吸振子在飞轮以2000 r/min恒定转速作用下的绝对加速度进行傅里叶变换,在频率域进行对比分析如图10所示。
由图10可见,飞轮恒定转速条件下其安装面输出扰动呈现典型的线谱特征,且离散分布在0 Hz~1000 Hz频率范围内。其中,在200 Hz以内频段的加速度线谱峰值较大,最大值约为0.06g/50 Hz。安装非线性能量阱后,该频点的幅值减小为0.029g/50 Hz,衰减量约为52%。
为了便于对比,将200 Hz以内频率范围内,安装非线性能量阱前后和吸振子的加速度响应峰值和频点如表1所示。可见,受非线性能量阱影响,多个频点的振动响应得到有效抑制。同时,非线性能量阱的振动响应峰值频点并非与飞轮系统振动响应严格一致。该现象表明,非线性能量阱可在较宽频段内产生振动响应,并有效抑制飞轮输出稳态载荷激励下的响应。但是,部分频点振动响应不降反增,原因在于非线性能量阱阻尼小,无法快速衰减能量,导致能量逆向流动作用于测试系统致使其响应增加。
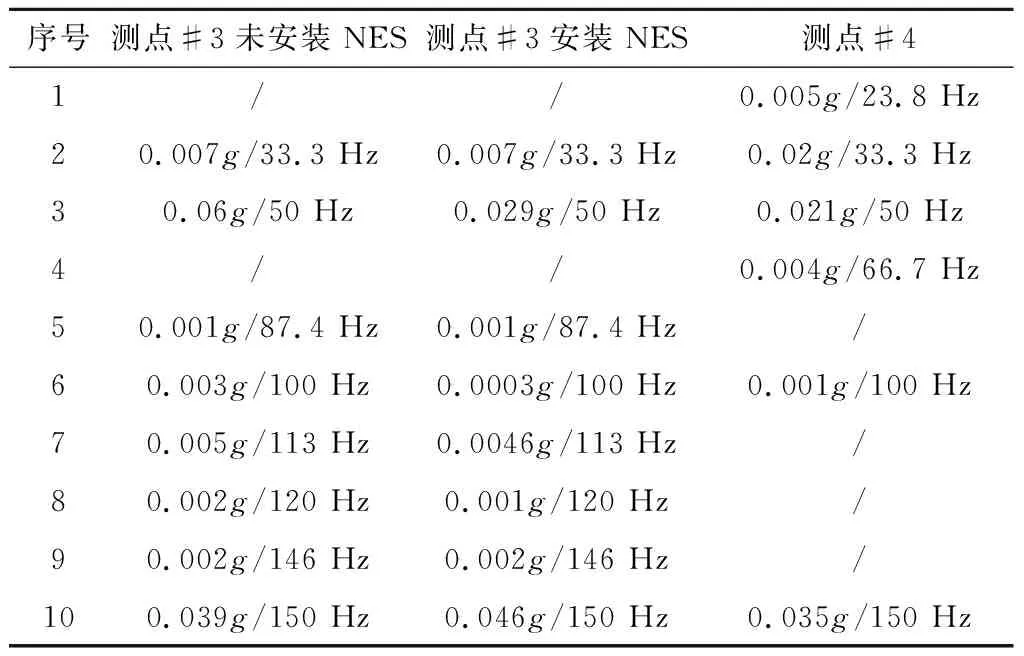
表1 飞轮安装面和非线性能量阱加速度响应Table 1 Acceleration in the flywheel position and the NES
4 结 论
本文以抑制航天器飞轮系统输出的宽频线谱和力学环境冲击载荷为目标。为了验证前期仿真分析结论和非线性能量阱的振动抑制效果开展了实验研究。通过数据分析得出如下结论:
(1)冲击载荷量级影响非线性能量阱的抑振效果,即:小量级条件下,柔性支架加速度响应未被有效抑制;量级增加其加速度响应峰值得到有效衰减。同时,非线性能量阱吸振子的振动响应显著;
(2)对比冲击载荷作用下,设备安装面和非线性能量阱吸振子的加速度频谱曲线,可以发现非线性能量阱的宽频抑振特征,即:设备安装面多个频点的加速度响应峰值被有效抑制;
(3)在飞轮宽频线谱扰动作用下,通过安装非线性能量阱可在较宽频带内有效抑制设备安装面的加速度响应峰值。
通过以上研究可为后续优化非线性能量阱及在航天器振动抑制领域的工程应用奠定技术基础。后续还将探索将单自由度非线性能量阱拓展为多自由度非线性能量阱的可行性及抑振效果评估。
参 考 文 献
[1] Bialke B. High fidelity mathematical modelling of reaction wheel performance [C]. Proceedings of the 21th Annual AAS Rocky Mountance Guidance and Control Conference AAS paper, 1998, 98: 483-496.
[2] Grogan R L, Masterson R A, Miller D W. Development and validation of reaction wheel disturbance models: empirical model [J]. Journal of Sound and Vibration, 2002, 249(3), 575-598.
[3] 邓瑞清, 赵岩, 房建成, 等. 磁悬浮飞轮与机械飞轮干扰特性的对比分析[J]. 宇航学报, 2016, 37(8):917-923. [Deng Rui-qing, Zhao Yan, Fang Jian-cheng, et al. Distrubance characteristics analysis of magnetically suspended and mechanical flywheels [J]. Journal of Astronautics, 2016, 37(8): 917-923.]
[4] Luo Q, Li D X, Zhou W Y, et. Al. Dynamic modelling and observation of micro-vibration generated by a single gimbal control moment gyro [J]. Journal of Sound and Vibration, 2013, 332(19): 4496-4516.
[5] 孟光, 周徐斌. 卫星微振动及控制技术进展[J]. 航空学报, 2015, 36(8): 36-40. [Meng Guang, Zhou Xu-bin. Progress review of satellite micro-vibration and control [J]. Acta Aeronautica et. Astronautica Sinica, 2015, 36(8): 36-40.]
[6] 徐超, 李瑞杰, 游少雄. 卫星飞轮支架的共固化阻尼减振设计[J]. 宇航学报, 2010, 31(3): 907-911. [Xu Chao, Li Rui-jie, You Shao-xiong. Passive vibration control design with co-curing damping composite for a satellite flywheel bracket [J]. Journal of Astronautics, 2010, 31(3): 907-911.]
[7] 张庆君, 王光远, 郑钢铁. 光学遥感卫星微振动抑制方法及关键技术[J]. 宇航学报, 2015, 36(2): 125-132. [Zhang Qing-jun, Wang Guang-yuan, Zheng Gang-tie. Micro-vibration attenuation methods and key techniques for optical remote sensing satellite [J]. Journal of Astronautics, 2015, 36(2): 125-132.]
[8] 关新, 王全武, 郑钢铁. 飞轮拟主动隔振方法[J]. 宇航学报, 2010, 31(7):1870-1876. [Guan Xin, Wang Quan-wu, Zheng Gang-tie. A pseudo-acitve vibration isolation method for reaction wheels [J]. Journal of Astronautics, 2010, 31(7): 1870-1876.]
[9] 刘海平, 王耀兵, 史文华. 非线性能量阱对飞轮扰振特性的抑制[J]. 宇航学报, 2017, 38(5):490-496. [Liu Hai-ping, Wang Yao-bing, Shi Wen-hua, Vibration suppression for a flywheel based on nonlinear energy sink [J]. Journal of Astronautics, 2017, 38(5): 490-496.]
[10] Liu H P, Wang Y B, Sun P F, et al. Analysis of the dynamics of the flywheel with nonlinear vibration absorber using wavelets[C]. 24th International Congress on Sound and Vibration, London, British, July 23-27, 2017.
[11] 刘海平, 王耀兵. 一种非线性能量阱的构建及瞬态特征分析[J]. 振动与冲击, 2018,37(1):55-60.[Liu Hai-ping, Wang Yao-bing. Construction and study on dynamic performance of a novel nonlinear energy sink under transient excitation [J], Journal of Vibration and Shock, 2018,37(1):55-60.]
