考虑高耗时约束的全电推进卫星多学科优化
2018-06-04李怀建史人赫
袁 斌,刘 莉,李怀建,龙 腾,史人赫
(北京理工大学宇航学院,北京 100081)
0 引 言
相比于传统化学推进卫星,全电推进卫星采用高比冲的电推进系统完成地球同步轨道转移、地球静止轨道(GEO)位置保持以及寿命末期离轨等任务,能够大幅缩减推进剂携带量,从而实现“一箭双星”发射,对于降低卫星研制成本、提高卫星有效载荷比等方面具有重要意义[1]。目前波音、洛马等众多公司均开展了全电推进卫星的研制[2-3],在未来的卫星市场中,全电推进卫星将扮演重要角色。
由于电推进系统推力较小(几十至几百毫牛),全电推进卫星地球同步轨道转移时间较传统化学推进卫星大幅延长(一般需3至6个月),较长的变轨周期还导致卫星长期运行在辐射带中,造成太阳翼性能退化与输出功率降低,对卫星抗辐射能力与供配电系统等方面的设计提出了新的技术挑战。由于全电推进卫星系统设计是一个多学科耦合的复杂工程问题,有必要采用多学科设计优化(Multidisciplinary design optimization, MDO)方法[4]进行设计优化以提高卫星整体性能、降低研制成本。众多学者已经将MDO方法初步应用于卫星设计[5-9],并取得了部分研究成果。
然而,在航天器系统实际设计中需要调用高精度仿真分析模型(如有限元模型等)以提高设计可信度,导致了优化成本急剧增加。此外,航天器MDO问题往往需要通过多学科分析(Multi-disciplinary analysis, MDA)过程进行迭代求解,从而进一步加剧计算复杂性[10]。为了缓解航天器MDO所面临的计算复杂性问题,基于代理模型的优化方法(Surrogate-based analysis and optimization, SBAO)近年来得到了国内外学者的普遍关注。SBAO方法旨在通过构建计算量小且与原模型精度相当的代理模型,替代原高精度模型(或MDA过程)用于设计优化[11]。文献[12]指出SBAO对于提高现代航空航天系统的性能,降低其设计成本具有重要意义。文献[10-11]对SBAO的研究进展进行了详细的综述。
常见的SBAO方法包括高效全局优化方法[13]、追峰采样方法[14]、序列径向基函数[15-16]等。其中,
高效全局优化方法(Efficient global optimization, EGO)具有良好的收敛性及求解效率,该方法通过获取少量样本点构造Kriging代理模型,并依据期望改善(Expected improvement, EI)准则新增样本点更新代理模型,直至收敛至全局最优解。但是传统EGO方法无法处理高耗时约束优化问题,限制了其在工程领域中的应用。本文针对全电推进卫星MDO问题,考虑轨道转移、位置保持、空间环境、供配电及结构等学科,以整星质量最小为目标建立全电推进卫星MDO模型,并基于增广拉格朗日乘子法提出一种考虑高耗时约束的高效全局优化方法(ALM-EGO),以实现全电推进卫星MDO问题的高效求解。
1 学科分析模型
考虑到全电推进卫星推力小、变轨时间长以及辐射环境恶劣等特点,本文参考文献[17],主要考虑轨道转移、位置保持、空间环境、供配电、结构及质量学科建立系统MDO模型,其设计结构矩阵(DSM)如图1所示,图中各参数定义如表1所示。下面对各学科建模方法进行简要说明。

变量名变量定义变量名变量定义Mini位置保持阶段初始质量Msolar太阳翼质量Lr卫星处于辐射带中的位置参数Msatellite整星质量MGTO轨道转移消耗推进剂质量Mstructure卫星结构质量MGEO位置保持消耗推进剂质量Mbat蓄电池质量pr太阳翼功率下降系数
1.1 轨道转移学科
轨道转移学科分析的目的是获取转移时间Tf,推进剂消耗量MGTO及卫星在辐射带中的位置信息,设计变量为两个阶段的推力角α,β,φ。
由于电推进系统推力较小,与卫星所受到的摄动加速度处于同一量级,可将电推进加速度作为摄动加速度处理,建立小推力轨道转移动力学方程如下所示[18]:
式中:各参数定义可参考文献[18]。转移过程中保持推力大小不变。
卫星初始位于近地点几百千米,远地点位于地球同步轨道的大椭圆GTO轨道。本文采用推力方向固定的两阶段变轨策略[18],使用连续电推进的方式使卫星由GTO轨道向GEO轨道转移,并考虑地球阴影对于轨道转移过程的影响。当卫星位于地影区时,电推力器关机,其余时间电推力器全程开机,地球阴影模型参考文献[17]。转移第一阶段的任务是抬高半长轴,同时降低轨道倾角,直至轨道半长轴到达静止轨道半径。第一阶段推力方向由两个定义于RTN系的推力角α及β定义,如图2(a)所示。第二阶段的任务是将偏心率和倾角降低至零,从而使卫星进入GEO轨道,该阶段推力方向由定义于PQW系的推力角φ决定,其定义如图2(b)所示。具体坐标系定义参考文献[18]。
在轨道学科需满足的约束条件如下所示:
Tf≤180 天
(2)
1.2 位置保持学科
位置保持学科分析的目的是获取东西方向位保精度lmax,南北方向位保精度imax及整个位置保持过程所消耗的推进剂量MGEO,设计变量为推力器的安装位置。
本文基于文献[19]中的位保策略,建立全电推进卫星完备状态下的小推力位置保持模型。卫星上共装有四个推力器,关于质心对称安装于背地板上,且推力方向通过质心,其位置定义在TNR坐标系中。TNR坐标系及推力器安装位置如图3所示。
由于GEO轨道倾角和偏心率均为零,为避免动力学方程奇异,本文采用无奇点轨道要素描述GEO轨道,GEO轨道脉冲推力控制方程参考文献[19]。
本文以2天为一个位保小周期,7个小周期构成一个完整的位保周期,总位保时间为15年。每个小周期中每个推力器仅开机一次,顺序为推力器1-推力器4-推力器2-推力器3,其中推力器1和推力器2开机赤经相同,推力器3和推力器4开机赤经相同,两组开机赤经相差180°,根据脉冲推力控制方程和推力矢量余弦,获得小控制周期内各推力器产生的速度增量,继而得到该小控制周期内卫星的位移。
位置保持学科需满足的约束条件如下所示:
(3)
1.3 空间环境学科
空间环境学科分析的目的是获取太阳翼功率下降系数pr,如下所示[17]:
(4)
式中:Dd为质子位移损伤,由轨道转移阶段卫星位于辐射带中的位置信息决定,Dx及K均为太阳翼材料系数,Dx取值为3.52×109,K取值为0.135。具体计算流程参考文献[17]。
1.4 供配电学科
供配电学科分析的目的分为三部分。第一部分是根据太阳翼功率下降系数,计算太阳翼寿命初期输出功率PBOL和寿命末期输出功率PEOL[20]。第二部分是根据蓄电池容量Cs,计算蓄电池质量Mbat及蓄电池放电深度DOD,其具体计算流程同样参考文献[20]。第三部分是根据太阳翼面积Asa获取太阳翼质量Msol[21]。
供配电学科需满足的约束条件如下所示:
(5)
1.5 结构学科
结构学科分析的目的是获取卫星结构质量Mstr,卫星轴向频率fax及侧向频率flat,设计变量为承力筒直径DT。
本文研究的全电推进卫星采用中心承力筒结构。为减小模型复杂程度,提高设计效率,本学科采用文献[22]中的经验公式进行卫星结构分析。卫星轴向频率fax及侧向频率flat的经验公式如式(6)所示。
(6)
式中:E为杨氏模量,取值为7.06×1010N/m2,A为承力筒横截面积,hs为卫星本体高度。本文中,卫星尺寸取1.9(x)×1.9(y)×2.5(z),η1和η2分别为整星轴向频率与侧向频率的修正因子,其取值基于文献[23]中的试验数据求得。本文中η1和η2的取值分别为0.0725和0.16。
本文中卫星采用复合材料,包括一层芯子及4层铺层,芯子密度为30.95 kg/m3,铺层密度为2800 kg/m3。结构质量由材料密度乘以材料体积求得。
结构学科需满足的约束条件如下所示:
(7)
1.6 质量分析
质量分析学科主要目的是获取卫星整星质量Ms作为MDO问题的优化目标函数,其计算方法如式(8)所示。
Ms=MGTO+MGEO+Mstr+Msol+
Mbat+Mpay+Moth
(8)
式中:Ms为整星质量,Mpay为有效载荷质量,取值为500 kg,Moth为卫星其余部分质量,取值为400 kg。由图1可知,Ms为反向耦合变量,需采用定点迭代方法获取满足系统一致性约束的设计方案。
2 考虑高耗时约束的高效全局优化方法
针对现有大部分SBAO方法(如EGO,MPS等)无法处理复杂工程问题中的高耗时约束的问题,本文提出一种基于增广拉格朗日乘子法的高效全局优化方法(Augmented Lagrange multiplier based efficient global optimization, ALM-EGO)来实现高效求解包含高耗时约束的全电推进卫星MDO问题。EGO以Kriging为代理模型,并引入期望改善度(Expected improvement, EI)作为采样准则,通过在EI最大值处新增样本点实现对代理模型的更新,从而引导算法快速收敛,具体流程参考文献[13]。
传统的工程设计优化问题如下所示:
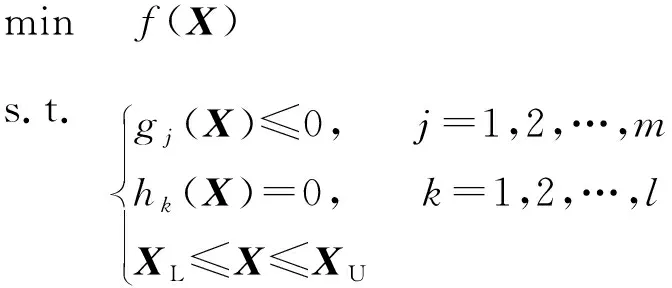
minf(X)s.t.gj(X)≤0,j=1,2,…,mhk(X)=0,k=1,2,…,lXL≤X≤XU
(9)
式中:f(X)为原目标函数,g(X)为不等式约束,h(X)为等式约束,XL和XU分别为设计空间的下界和上界。通过引入增广拉格朗日乘子构造增广目标函数为:
(10)
(11)
通过构造增广目标函数F(X)可将原约束优化问题转化为无约束优化问题。ALM-EGO主要思想为利用EGO方法对近似增广目标函数F(X)进行序列求解,直至获得满足约束的优化结果。同时为避免多次调用分析模型,分别对目标函数及各个约束条件分别构造Kriging代理模型,在求解EI时以目标函数及约束条件的预测值替代真实值,从而达到降低设计成本,提高优化效率的目的。
ALM-EGO计算流程如图4所示,具体计算步骤如下。
步骤1:确定优化问题的设计空间、初始样本点数量nini,最大样本点数量nmax,λ及rp初始值。采用拉丁超立方试验设计方法(Latin hypercube design, LHD)获取初始样本点,令当前样本点数量np=nini,迭代次数p=1。
步骤2:计算各初始样本点或新增样本点的真实模型响应值。
步骤3:根据式(10)求解各样本点处增广目标函数值,并将最小值点作为当前最优解X*;若样本点数量已达到最大样本点数量,则算法结束,输出可行最优解;否则,算法进入步骤4。
步骤4:基于已有样本点,分别对目标函数和各约束条件构造Kriging代理模型,之后根据增广拉格朗日乘子法,利用目标函数与约束条件代理模型的信息构造近似增广目标函数及EI准则,如式(12)和(13)所示:
(12)
(13)
(14)
步骤6:若p=1,则令λ和rp的值分别为1=[1,1,…,1](m+l)×1和1,否则按式(15)更新λ及rp。令p=p+1,算法返回步骤2,继续迭代。
(15)
本文选用G 4数值算例[16]及弹簧设计问题(Sp-ring design, SD)[24]两个标准测试算例测试ALM-EGO在求解包含高耗时约束的工程优化问题时的性能。本文采用模型调用次数(Nfe)衡量算法效率。分别使用遗传算法(GA)、基于动态罚函数的高效全局优化方法(C-EGO)[25]及ALM-EGO方法三种算法对两个优化问题进行连续15次优化,其中,GA使用MATLAB中ga工具包缺省设置,C-EGO及ALM-EGO人为设置为同样的迭代次数,SD问题最大迭代次数为140,G 4问题最大迭代次数为120。优化最优解及模型调用次数对比如表2~3所示。
优化结果表明,对于SD问题,ALM-EGO可以收敛到理论最优解,而C-EGO及GA所得最优解分别与理论最优解相差35%及75%;对于G 4问题,ALM-EGO所求得的最优解于理论最优解仅相差1%左右,而C-EGO与GA所得最优解与理论最优解分别相差2.7%及2.0%左右。此外,ALM-EGO求解上述两组优化设计问题的计算成本仅为GA的14%~18%。综上所述,相比于GA与C-EGO,ALM-EGO在处理包含高耗时约束的优化问题时在最优性与效率方面均具有显著优势,验证了ALM-EGO的有效性。

表2 优化所得最优解对比Table 2 Comparison results of objective value

表3 优化过程所需模型调用次数对比Table 3 Comparison results of Nfe
3 全电推进卫星系统优化设计结果与分析
本节基于ALM-EGO方法求解全电推进卫星MDO问题。为了兼顾计算成本与收敛性,ALM-EGO初始样本点数量设为100,每次迭代新增一个样本点,最大样本点数量为300。本文研究的全电推进卫星中,电推进系统比冲为4000 s,单个推力器功率为4.5 kW,最大推力为200 mN。在轨道转移过程中,总推力为200 mN×2,初始GTO轨道根数为a=24328 km,e=0.7296,i=23.5°,ω=180°,Ω=90°,M=0°。卫星GEO定点位置为东经120 °。各设计变量初始值依照工程经验选取,得到优化前后的设计变量如表4所示,对应约束值如表5所示,优化前后的整星质量如表6所示。
从表4和表6可以看出,在轨道转移学科中,通过调整两阶段推力角,轨道转移时间缩短了24天左右,相应减少了约21.6 kg的推进剂。此外,在位置保持阶段,推力器安装位置的N坐标增加、T坐标减小,从而提高了南北位保效率。考虑到南北位保所消耗的推进剂要远高于东西位保,因此提高南北位保效率可有效减少推进剂消耗量。在优化方案中,整个位置保持阶段所需推进剂质量减少约9.96 kg。此外,在满足卫星功率要求的基础上,太阳翼面积减小了12.53 m2,质量降低了35.46 kg;电池容量减少了20.05 Ah,质量降低了97.22 kg。然而,由于初始设计方案不满足卫星轴向频率约束,因此卫星承力筒直径略有增加,提高了卫星轴向频率,但卫星结构质量相应增加了约3.17 kg。
综上所述,相比于初始设计方案,优化方案满足所有设计约束,同时整星质量降低了约161.09 kg,对于提高卫星有效载荷比、降低卫星发射成本等方面具有重要意义,从而验证了全电推进卫星MDO模型的合理性以及ALM-EGO方法的工程实用性。
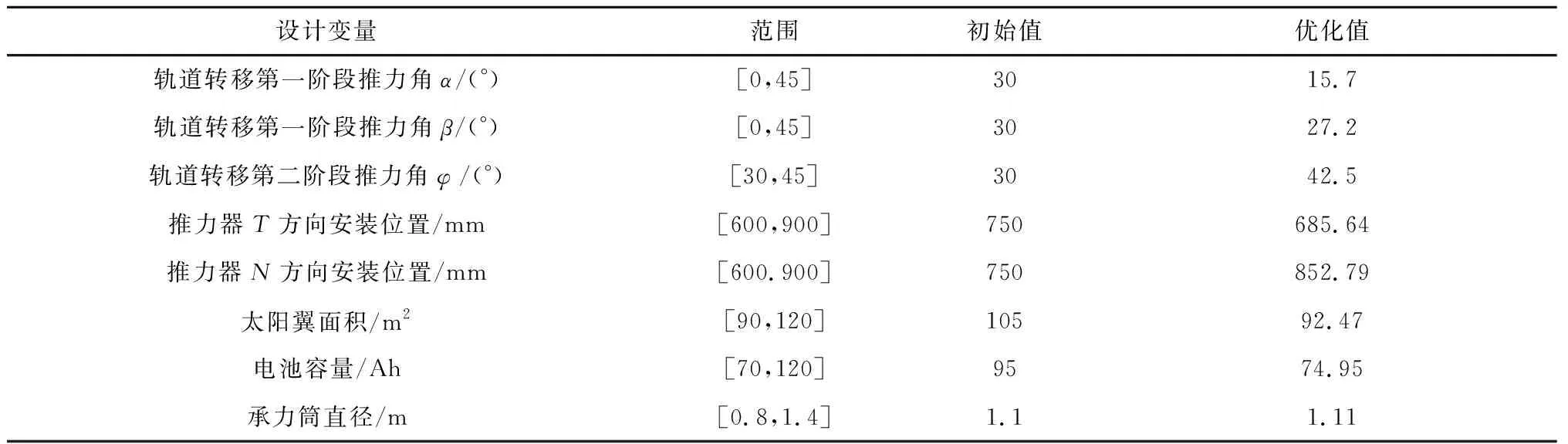
表4 初始方案及优化方案设计变量对比Table 4 Design variable of initial and optimal design
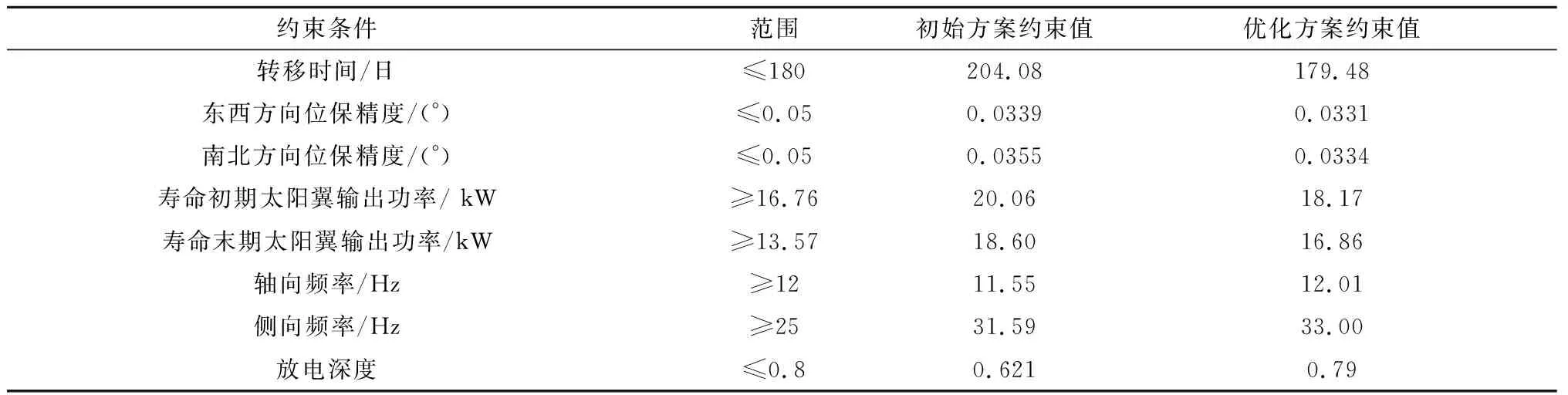
表5 初始方案及优化方案约束条件对比Table 5 Constraints of initial design and optimal design

表6 初始方案及优化方案目标函数对比Table 6 Initial and optimal objective value
4 结 论
1)本文针对全电推进卫星多学科设计优化问题,建立了系统设计结构矩阵并梳理了学科间数据关系,并在此基础上建立了考虑轨道转移、位置保持、空间环境、供配电、结构及质量分析学科的全电推进卫星MDO分析模型。
2)针对传统EGO问题无法处理约束的缺陷,引入增广拉格朗日乘子法,提出一种考虑高耗时约束的高效全局优化方法ALM-EGO,拓展了EGO在航天器设计领域的应用。通过两个标准测试算例对ALM-EGO的性能进行了测试,测试结果表明,ALM-EGO可在较少的模型调用次数下获得满足约束的优化解,具有较高的优化效率及全局收敛性。
3)将ALM-EGO应用于全电推进卫星多学科设计优化实例中,获得了满足约束的优化设计方案。相比于初始方案,整星质量降低了约161.09 kg,对于降低卫星发射成本,提升卫星整体性能具有重要意义。
4)本文所建立全电推进卫星MDO模型及设计优化框架可为其他全电推进航天器系统设计优化提供参考。
参 考 文 献
[1] 周志成, 高军. 全电推进GEO卫星平台发展研究[J]. 航天器工程, 2015, 24(2): 1-6. [Zhou Zhi-cheng, Gao Jun. Development approach to all-electric propulsion GEO satellite platform[J]. Spacecraft Engineering, 2015, 24(2): 1-6.]
[2] Feuerborn S A, Perkins J, Neary D A. Finding a way: Boeing’s all electric propulsion satellite[C]. AIAA/ASME/SAE/ASEE Joint Propulsion Conference, San Jose, USA, July 14-17, 2013.
[3] 胡照, 王敏, 袁俊刚. 国外全电推进卫星平台的发展及启示[J]. 航天器环境工程, 2015, 32(5): 566-570. [Hu Zhao, Wang Min, Yuan Jun-gang. A review of the development of all-electric propulsion platform in the world[J]. Spacecraft Environment Engineering, 2015, 32(5): 566-570.]
[4] Sobieszczanski-Sobieski J, Haftka R T. Multidisciplinary aerospace design optimization: survey of recent developments[J]. Structure and Multidisciplinary Opitimization, 1997, 14(1): 1-23.
[5] 陈琪峰, 戴金海. 卫星星座系统多学科设计优化研究[J]. 宇航学报, 2003, 24(5): 502-509. [Chen Qi-feng, Dai Jin-hai. Multidisciplinary design optimization of satellite constellation system[J]. Journal of Astronautics, 2003, 24(5): 502-509.]
[6] 姚雯, 陈小前, 赵勇. 基于不确定性MDO的卫星总体设计优化研究[J]. 宇航学报, 2009, 30(5): 1808-1815. [Yao Wen, Chen Xiao-qian, Zhao Yong. Research on satellite system design based on uncertainty multidisciplinary design optimization[J]. Journal of Astronautics, 2009, 30(5): 1808-1815.]
[7] 吴蓓蓓, 黄海, 陈珅艳, 等. 使用解析目标分流策略的海洋卫星多学科优化[J]. 宇航学报, 2013, 34(1): 9-16. [Wu Bei-bei, Huang Hai, Chen Shen-yan, et al. Multi-disciplinary design optimization of ocean satellites based on analytical target cascading strategy[J]. Journal of Astronautics, 2013, 34(1): 9-16.]
[8] 彭磊, 刘莉, 龙腾, 等. 一种基于推进剂消耗优化的卫星小推力器布局设计[J]. 宇航学报, 2015, 36(3): 268-277. [Peng Lei, Liu Li, Long Teng, et al. Satellite thruster configuration design based on propellant consumption optimization[J]. Journal of Astronautics, 2015, 36(3): 268-277.]
[9] Huang H, An H C, Wu B B, et al. A non-nested collaborative optimization method for multidisciplinary design optimization and its application in satellite designs[J]. Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering, 2016, 230(12): 2292-2305.
[10] 龙腾, 刘建, Wang G G, 等. 基于计算试验设计与代理模型的飞行器近似优化策略探讨[J]. 机械工程学报, 2016, 52(14): 79-105. [Long Teng, Liu Jian, Wang G G, et al. Discuss on approximate optimization strategies using design of computer experiments and metamodels for flight vehicle design[J]. Journal of Mechanical Engineering, 2016, 52(14): 79-105.]
[11] Forrester A I J, Keane A J. Recent advances in surrogate-based optimization[J]. Progress in Aerospace Sciences, 2009, 45(1): 50-79.
[12] Queipo N V, Haftka R T, Wei S, et al. Surrogate-based analysis and optimization[J]. Progress in Aerospace Sciences, 2005, 41(1): 1-28.
[13] Jones D R, Schonlau M, Welch W J. Efficient global optimization of expensive black-box functions[J]. Journal of Global Optimization, 1998, 13(4): 455-492.
[14] Wang L Q, Shan S Q, Wang G G. Mode-pursuing sampling method for global optimization on expensive black-box functions[J]. Engineering Optimization, 2004, 36(4): 419-438.
[15] Peng L, Liu L, Long T, et al. Sequential RBF surrogate-based efficient optimization method for engineering design problems with expensive black-box functions[J]. Chinese Journal of Mechanical Engineering, 2014, 27(6): 1099-1111.
[16] Shi R H, Liu L, Long T, et al. Sequential radial basis function using support vector machine for expensive design optimization[J]. AIAA Journal, 2017, 55(1): 214-227.
[17] Shi R H, Liu L, Long T, et al. Surrogate assisted multidisciplinary design optimization for an all-electric GEO satellite [J]. Acta Astronautica, 2017, 138: 301-317.
[18] 马雪, 韩冬, 汤亮. 电推进静止轨道转移与空间环境分析[J]. 空间控制技术与应用, 2015, 41(1): 31-35. [Ma Xue, Han Dong, Tang Liang. On the electric-propulsion-based geostationary transfer and space environmental analysis[J]. Aerospace Control and Application, 2015, 41(1): 31-35.]
[19] Zhang J R, Zhao S G, Zhou Z C, et al. Optimal station keeping for XIPS thrusters in failure mode under eclipse constraints [J]. Journal of Aerospace Engineering, 2016, 29(6): 04016041.
[20] 周志成. 通信卫星工程[M]. 北京: 中国宇航出版社, 2014.
[21] Huang H, An H C, Wu W R, et al. Multidisciplinary design modeling and optimizationfor satellite with maneuver capability [J]. Structural and Multidisciplinary Optimization, 2014, 50(5): 883-898.
[22] 谭春林, 庞宝君, 张凌燕, 等. 对地观测卫星总体参数多学科优化[J]. 北京航空航天大学学报, 2008, 34(5): 529-532. [Tan Chun-lin, Pang Bao-jun, Zhang Ling-yan, et al. Multidisciplinary optimization in earth observation satellite main parameters[J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(5): 529-532.]
[23] Wu W R, Huang H, Chen S Y, et al. Satellite multidisciplinary design optimization with a high-fidelity model[J]. Journal of Spacecraft and Rockets, 2015, 50(2): 463-466.
[24] Long T, Wu D, Guo X S, et al. Efficient adaptive response surface method using intelligent space exploration strategy[J]. Structural and Multidisciplinary Optimization, 2015, 51(6): 1335-1362.
[25] 刘建. 基于动态代理模型的对地观测卫星多学科设计优化研究 [D]. 北京: 北京理工大学, 2016. [Liu Jian. Multidisciplinary design optimization using dynamic metamodel for earth observation satellite [D]. Beijing: Beijing Institute of Technology, 2016.]
