火星进入器壁面脉动压力环境数值模拟
2018-06-04石小潘荣吉利
石小潘,赵 瑞,荣吉利,袁 武
(1. 北京理工大学宇航学院,北京 100081;2. 中国科学院计算机网络信息中心超级计算中心,北京 100190)
0 引 言
随着航天技术的不断进步和发展,人类已经展开了200多次的深空探测任务[1]。而火星作为距离地球最近的地外行星,和其他行星相比其自然环境更接近地球,因此,火星成为人类探索宇宙重要的一部分。火星和地球一样存在大气层,火星大气主要由95.7%的CO2,2.7%的N2和1.6%的Ar组成,密度只有地球的1%,与地球大气组分显著不同。文献[2]指出大气中的主要气体成分的物理化学性质对气动特性有显著影响,因此,进入器进入火星大气与再入地球大气时受到的气动环境会有所差异。目前,各国开展火星无人进入或软着陆探测任务时,发射的进入器均采用钝体大底-倒锥布局的外形[3],优点是在高超声速进入时其布局外形的高阻力特性有利于进入器的气动减速。而进入器在进入火星大气层时,由于钝体绕流效应,流体绕过肩部后出现分离,在舱体尾段及配平翼迎风面底端形成了分离区,分离区内涡流脉动剧烈,将会在进入器壁面产生振幅较高的脉动压力,其频率范围包含了普通金属面板的共振频率。一方面,脉动压力可使进入器壁面出现较大的局部载荷,容易激起飞行器结构的抖振响应,缩短材料的疲劳寿命;另一方面,脉动压力作为一种随机激励以噪声的形式通过透射及结构共振转变为舱内噪声,直接影响到内部仪器的可靠性,甚至导致任务失败[4-5]。因此,研究火星进入器壁面的脉动压力环境,对火星进入器的结构设计及舱内声振环境的预测都具有重要的意义。
尽管若干火星着陆任务已经完成,但是与火星进入器相关的飞行试验数据依然很匮乏,并且模拟火星大气环境进行风洞试验难度大且成本高,因此对火星进入器的脉动压力环境的研究手段主要靠数值计算[6]。国外对飞行器脉动压力环境作了诸多研究,Plotkin等[7]通过对各种实验数据的分析,总结归纳了一套适用于跨声速范围内非定常流动脉动压力环境的经验公式,给出了均方根脉动压力系数、功率谱及空间相关性的计算方法。Tsutsumi等[8]采用改进的延迟脱体涡方法对典型整流罩进行非定常数值模拟,通过与实验值进行对比证明该方法的可行性。文献[9-11]采用脱体涡方法对亚声速、跨声速及超声速的钝体绕流流场作了数值模拟,模拟结果整体和实验数据相近,且在跨超声速精度最好。Ross等[12]针对在亚跨声速范围内钝体绕流非定常分离难以精确计算的问题,通过风洞实验分析了雷诺数、来流马赫数、攻角等对标准舱体外形脉动压力的影响。在国内,徐立功等[13]对机动再入飞行器壁面所受的空气动力脉动环境进行了分析,用统一的参变量给出了高超声速范围内飞行器壁面脉动压力统计特性的工程计算公式。张志成等[14]使用工程估算公式分析了来流攻角和来流马赫数对球头双锥体表面脉动压力分布的影响。蒋华兵等[15]通过对典型球头单锥飞行器定常时均流场的求解,获得湍流附面层厚度及外缘流动参数,并代入经验公式,对飞行器噪声环境进行计算并指出了飞行器表面噪声环境恶劣的区域。赵瑞等[16]分析了火箭整流罩外气动噪声环境,用隐式大涡模拟的方法对跨声速条件下火箭整流罩外部气动噪声进行数值分析,并改进了经验公式在分离区的预测精度;此外,赵瑞等[5]对跨声速旋成体火箭脉动压力产生的流场结构进行重新分区归纳,针对各个分区脉动流场提出改进的经验公式,提高预测精度。
综上所述,各国学者对飞行器脉动压力环境作了不同的研究,并取得了显著的成果,但对火星大气下进入器的脉动压力环境研究较少。进入器着陆火星表面要经历四个阶段:进入准备阶段、高超声速气动减速下降阶段、打开降落伞减速下降阶段和终点下降着陆阶段。本文将对进入器在开伞之前跨超声速气动减速下降阶段的脉动压力环境展开研究分析。基于脱体涡模拟(Detached eddy simulaion, DES)方法,通过对不同工况下进入器绕流进行非定常数值模拟,分析来流马赫数、来流攻角及配平翼展开角的变化对进入器壁面脉动压力环境的影响,综合评价进入器的脉动压力环境。
1 计算方法和模型
1.1 控制方程
流动控制方程为三维非定常可压缩N-S方程组,其在直角坐标系下的守恒积分形式可表示为:
(1)
式中:U为控制体, ∂U为控制面,Q为守恒变矢量,F为矢通量,n为边界的外法向量。
采用有限体积法对控制方程进行数值离散,在数值离散过程中,空间对流项离散使用5阶的WENO格式,黏性项使用4阶的中心差分方法[17]。时间推进采用二阶隐式双时间法进行迭代[18],内迭代选择常用的LU-SGS(lower-upper symmetric-Gauss-Seidel )方法[19]。定常计算采用一方程S-A湍流模型并将其计算结果作为非定常DES计算的初始流场。
目前对于火星大气介质的模拟,有两种方法:一种方法是采用真实气体模型[2],考虑气体介质中的各种化学组分;另一种方法是等效比热比模型[20],根据统计热力学的相关理论[21],标准状态的各种气体介质的热力学参数都可用峰值能量分配原理来描述,也就能用有效比热比、气体常数和温度等变量来表征。离解、电离等真实气体效应亦可看作能量分配方式的增加,进而带来更低的有效比热比,因此,非空气介质、真实气体效应等影响可以用有效比热比来等效和表征。本文使用的即是基于等效比热比方法进行数值计算,其等效比热比取为1.17[20]。另外,对于火星大气环境,以CO2为主,其黏性系数随温度而改变,使用Sutherland公式来表征
(2)
式中:参考黏性系数μ0=1.48×10-5kg/m·s,参考温度T0=293.15 K。和黏性力一样,气体微团之间的热传导也是由分子运动造成,导热系数和黏性系数之间存在相似关系,在处理高速黏性流动问题,导热系数由Pr=μcp/k确定,Pr=0.71。
1.2 基于S-A模型的DES方法
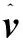
(3)
方程(3)右端的生成项变量定义为:
其中,Ω是涡量,d为到物面的最近距离,函数fW如下所示:

在S-A模型中定义湍流黏性系数为:
(4)
DES方法通过对Spalart-Allmaras湍流模型进行长度尺度修正,使其在近壁面采用雷诺平均方法(RANS)数值模拟附面层的流动,即用湍流模型来模拟近壁面的小尺度脉动;远离物面附面层的区域DES转换至Smagorinsky大涡模拟,成为亚格子雷诺应力模型。
(5)

(6)
1.3 计算模型和网格
本文主要研究进入器进入火星大气层之后,在减速降落伞打开之前的跨超声阶段来流马赫数(Ma)、来流攻角(α)及配平翼展开角(φ)对火星进入器壁面脉动压力环境的影响。计算工况如表1所示。

表1 进入器计算条件Table 1 Computation condition for the capsule
计算模型为类似文献[23]中所示的具有配平翼的进入器外形,基本尺寸如图1所示。计算网格为六面体结构化网格,如图2所示,网格总量约600万,并在分离区附近(配平翼及舱体后方)进行加密,用于捕捉脱体涡结构。壁面第一层网格保证y+<1,用于捕捉黏性边界层流动。
对进入器z=0截面进行测点采样,如图3所示,采样点共计29个,采样频率为5000 Hz,从瞬时流场中提取壁面特征点压力信号随时间变化历程曲线,获得均方根脉动压力系数,并采用快速傅里叶变换(FFT),研究频域空间中脉动压力的功率谱密度分布。
1.4 数值方法验证
为验证本文使用的计算方法,以具有风洞试验数据的神舟返回舱模型作为验证算例。神舟返回舱风洞外形及壁面测点的位置见图4,计算网格约为1000万,计算参数选自风洞实验参数见表2。

T0/KP0/PaMaU∞/(m·s-1)p∞/Paq∞/Pa(Re/L)/m-12871012090.6200.379297200471.213×107
2 结果与分析
2.1 来流马赫数对脉动压力环境的影响
均方根脉动压力系数是衡量壁面脉动压力总强度的关键统计参数。图7为在来流攻角为0°,配平翼展开180°时不同来流马赫数下进入器壁面各测点的均方根脉动压力系数对比曲线。
从图7可以看出,进入器整体的脉动压力环境随来流马赫数的增加呈降低的趋势,在马赫数为1.2时,均方根脉动压力系数第一峰值出现在舱体背风面下侧,第二峰值出现在配平翼背风面;另外,配平翼迎风面翼根区及舱体背风面上侧的脉动压环境也十分严峻。图8为不同来流马赫数下进入器对称面的马赫数云图。从图8可以看出,由于钝体效应,流动绕过肩部后出现分离,进入器舱体段淹没在分离区中。由于分离区内涡流的非定常脉动,在舱体壁面诱导产生了脉动压力。同时可以看到,在配平翼的迎风面翼根处也存在小的分离区。随着马赫数的增加,流动可压缩效应增强,使得舱体分离区逐渐减小。当马赫数较低时(见图8(a))分离区较大,涡流脉动强烈,使得舱体背风面及配平翼背风面的均方根脉动压力系数较大,脉动压力环境恶劣。相反,随着来流马赫数的增加,来流气体的可压缩性逐渐增强,分离区也越来越小,分离区较短,导致涡流脉动空间不足、发展不充分(见图8(b)和图8(c))。因此,在配平翼背风区及舱体背风区的均方根脉动压力系数较小,脉动压力环境并不严峻。
在进入器舱体下侧靠近肩部位置安装有配平翼,下侧气流绕过肩部后经膨胀激波加速后冲击在配平翼迎风面上,迎风面气流在配平翼驻点处分为上下两部分,上边的气流在舱翼连接的夹角范围内形成了一个低压分离区。在来流马赫数为1.2时,钝体前边形成的脱体激波强度较小且不稳定,在肩部膨胀激波和翼尖高压区的作用下,分离区极不稳定、运动剧烈,诱导出强烈的脉动压力环境,致使配平翼迎风面翼根处均方根脉动压力系数较大。而在来流马赫数为2和3时,钝体前方的脱体激波强度较大且稳定,并且从图8可以看出,脱体激波随着马赫数的增加逐渐向大底靠近。配平翼迎风面的分离区受脱体激波抑制作用逐渐增强,分离区的运动逐渐保持稳定。因此,分离区在配平翼迎风面诱导的脉动压力环境并不明显。下边的气流绕过配平翼之后,经配平翼诱导在其背风面产生一个分离区。在来流马赫数为1.2时,涡流运动剧烈,致使配平翼背风面的脉动压力环境剧烈。该涡流流场向下游发展,和舱体脱体涡区域相互干扰,使舱体背风面下侧靠近配平翼的区域脉动压力达到最大,即均方根脉动压力系数第一峰值所在的区域。相比舱体背风面下侧,舱体背风面上侧仅受舱体脱体涡的影响,其脉动压力环境相对较小。
如上所述,进入器脉动压力环境在低马赫数下最为严峻,以下对攻角和配平翼展开角的研究主要基于Ma=1.2来流条件。
2.2 来流攻角对脉动压力环境的影响
图9为在来流马赫数为1.2,配平翼展开180°时不同来流攻角下进入器壁面各测点的脉动压力系数变化曲线。从图9可以看出, 来流攻角从0°改变到15°,进入器整体的脉动压力环境变化较大。
图10为进入器在不同来流攻角下的马赫数云图。从图10可以看出,随着来流攻角的改变,进入器前方的脱体激波的位置向配平翼迎风面压进,使得来流在配平翼迎风面上的再附点位置向翼根靠近,如图11所示,再附点的位置改变使得分离区作用的区域向翼根缩进,从而使得在配平翼迎风面上诱导的脉动压力峰值向翼根区转移。另外,配平翼诱导的剪切层随着攻角的改变向舱体下侧面靠近,使得配平翼背风面及舱体背风面下侧的分离区减小,涡流脉动空间减小、脉动减弱,使得均方脉动压力系数相对减小;对于舱体背风面上侧,分离区增大,涡流脉动空间增大、脉动增强,使得舱体上侧面的均方根脉动压力系数相对增大。
2.3 配平翼展开角度对脉动压力环境的影响
图12为在来流马赫数为1.2,来流攻角0°时不同配平翼展开角度下进入器壁面各测点的均方根脉动压力系数变化曲线。从图12可以看出,配平翼角度变化对配平翼迎风面影响较大,对进入器其他区域影响较小。
图13为不同配平翼展开角度下舱翼连接段的局部放大图。从图13可以看出,流动绕过下侧肩部后出现分离,在配平翼展开角120°范围内,配平翼和舱体段淹没在分离区中,随着配平翼的展开,配平翼迎风面的分离区逐渐减小,涡流脉动空间不足,脉动强度逐渐减弱,因此在配平翼迎风面上诱导产生的脉动压力逐渐减小。相反,背风区的脉动压力稍有增加。配平翼展开150°时,部分来流冲击在配平翼迎风面上,来流受配平翼的影响,在舱翼连接段形成了一个低压分离区,分离区再附点位置(见图13(c))极不稳定,前后移动剧烈,将在配平翼迎风面上诱导产生脉动压力峰值,均方根脉动压力系数最大达到0.21。另外,再附点的前后移动加剧了分离区运动,将会在配平翼迎风面靠近翼根区域诱导严峻的脉动压力环境。配平翼展开180°时,配平翼迎风面分离区再附点位置基本固定,相比配平翼展开150°,分离区的形态较稳定。因此,分离区在配平翼上诱导的脉动压力得到减缓。
2.4 脉动压力频谱特性
功率谱密度表征脉动能量随频率的分布特性。通过对火星进入器脉动压力的频谱特性分析,可以确定脉动能量集中的频率区间,进而对进入器进行针对的结构设计。针对进入器脉动压力环境最恶劣的工况(来流马赫数1.2,配平翼展开150°),选取三个不同区域特征点进行功率谱密度分析,其中测点11位于配平翼迎风面分离区靠近翼根处,测点13位于配平翼再附点位置附近,测点25位于舱体段分离区。图14为上述3个典型位置测点的功率谱密度频谱变化曲线。从图14可以看出,在测点11位置(见图14(a)),该处位于舱翼连接段这个狭小的空间内,脉动频率主要受分离区脉动频率影响,在200 Hz左右达到峰值,脉动能量达10 Pa2·Hz-1。测点13与测点11类似,脉动能量集中频率受分离区脉动频率影响(见图14(b)),但该位置处于再附点位置前后移动范围,能量幅值在200 Hz左右达100 Pa2·Hz-1,相比其他区域高出一个量级,在结构设计中需要着重考虑。在测点25位置(见图14(c)),舱体分离区内脉动压力主要由舱体诱导的大分离涡流脉动所致,能量主要集中在低频区域(10 Hz左右)。
3 结 论
本文使用DES方法研究来流马赫数、来流攻角及配平翼展开角等因素对火星进入器壁面脉动压力环境的影响规律,并得出以下结论:
1)采用DES方法对进入器壁面脉动压力环境进行预测,能够较为准确地获得壁面脉动压力的均方根系数以及频谱特性。
2)在跨超声速来流条件下,随着来流马赫数增加,舱体背风面分离区的可压缩性逐渐增强,分离区逐渐减小,涡流脉动空间不足,致使舱体背风面的脉动压力环境逐渐减弱。因此,在跨声速时火星进入器壁面脉动压力环境最为恶劣。
3)配平翼迎风面分离区受脱体激波的影响显著:来流马赫数较小时,脱体激波强度较小且不稳定,对翼根分离区抑制作用较弱,分离区运动剧烈,将会诱导强烈的脉动压力环境;来流马赫数较大时,脱体激波强度较大且稳定,对翼根分离区抑制作用较强,分离区运动平缓,诱导的脉动压力环境较弱。
4)来流攻角改变使来流在配平翼迎风面上分离区再附点的位置向翼根方向转移,使得当地的脉动压力趋于恶劣。翼根区位于舱翼连接段,其结构稳定性在设计中需要着重注意。
5)配平翼展开150°时,配平翼迎风面分离区再附点的位置极不稳定、前后移动剧烈,将在配平翼迎风面诱导产生脉动压力峰值,脉动能量主要集中在中频区域;配平翼展开180°时,配平翼迎风面分离区再附点的位置基本固定,在配平翼迎风面上诱导的脉动压力环境得到减缓。
参 考 文 献
[1] 叶培建, 杨孟飞, 彭兢, 等. 中国深空探测进入/再入返回技术的发展现状和展望[J]. 中国科学, 2015, 45(3):229-238. [Ye Pei-jian, Yang Meng-fei, Peng Jing, et al. Review and prospect of atmospheric entry and earth reentry technology of China deep space exploration [J]. Science China Press, 2015, 45(3): 229-238.]
[2] 吕俊明, 苗文博, 程小丽, 等. 火星大气模型参数对MSL气动特性的影响[J]. 空间科学学报, 2014, 34(4):377-383. [Lv Jun-ming, Miao Wen-bo, Cheng Xiao-li, et al. Impact of martian atmosphere model parameters on aerodynamic characteristics of Mars science laboratory [J]. Chinese Journal of Space Science, 2014, 34(4): 377-383.]
[3] 陈冰雁, 詹惠玲, 周伟江. 防热大底外形对火星探测器气动特性的影响分析[J]. 宇航学报, 2016, 37(4):388-396. [Chen Bing-yan, Zhan Hui-ling, Zhou Wei-jiang. Investigation on influence of heatshield shape changes on aerodynamic design for Mars entry capsule [J]. Journal of Astronautics, 2016, 37(4): 388-396.]
[4] 龙万花, 陈伟芳, 宋松和. 旋成体跨声速脉动压力环境分析与预测[J]. 国防科技大学学报, 2004, 26(1):17-20. [Long Wan-hua, Chen Wei-fang, Song Song-he. Analysis and prediction of the fluctuating pressure induced by rotated aircraft at transonic Mach number [J]. Journal of National University Technology, 2004, 26(1): 17-20.]
[5] 赵瑞, 荣吉利, 任方, 等. 一种改进的跨声速旋成体壁面脉动压力经验预测公式[J]. 宇航学报, 2016, 37(10):1179-1184. [Zhao Rui, Rong Ji-li, Ren Fang, et al. Improvement of the fluctuating pressure empirical functions for a body of revolution at transonic Mach numbers [J]. Journal of Astronautics, 2016, 37(10): 1179-1184.]
[6] Wright M J, Tang C Y, Edquist K T, et al. A review of aerothermal modeling for Mars entry mission[C]. The 48th AIAA Aerospace Science Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, USA, Jan 4-7, 2010.
[7] Plotkin K J, Robertson J E. Prediction of space shuttle fluctuating pressure environment, including rocket plume effects [R]. NASA-CR-124347, June 1973.
[8] Tsutsumi S, Takama Y, et al. Hybrid LES/RANS simulations of transonic flowfield around a rocket fairing[C]. The 30th AIAA Applied Aerodynamics Conference, New Orleans,Louisiana, USA, Jun 25-28, 2012.
[9] Alan M, Graham V. Validation of DES for capsule aerodynamics using 05-CA wind tunnel test data[C]. The 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, Texas, USA,Jan 7-10, 2013.
[10] Alan M, Graham V. Detached-eddy simulation of capsule wake flows and comparison to wind-tunnel test data [J]. Journal of Spacecraft and Rockets, 2015, 52 (2):439-449.
[11] Josepf M, Pramod K, Graham V. Detached-eddy simulations of hypersonic capsule wake flow [J]. AIAA Journal, 2015, 53 (1):70-80.
[12] Ross J C, Burnside N J. Unsteady pressures on a generic capsule shape[C]. The 53rd AIAA Aerospace Sciences Meeting, Kissimmee, Florida, USA, Jan 5-9, 2015.
[13] 徐立功, 刘振寰. 再人飞行器脉动压力环境的分析与预测[J]. 空气动力学学报, 1991, 9(4):457-464. [Xu Li-gong, Liu Zhen-huan. Prediction of maneuvering reentry vehicles fluctuating pressure environments [J]. Acta Aerodynamic Sinica, 1991, 9(4): 457-464.]
[14] 张志成, 陈伟芳, 石于中, 等. 球头双锥再入体表面脉动压力环境的分析与预测[J]. 宇航学报, 2002, 23(2):19-22. [Zhang Zhi-cheng, Chen Wei-fang, Shi Yu-zhong, et al. The analysis and prediction of fluctuating pressure on the spherebiconic reentry vehicle [J]. Journal of Astronautics, 2002, 23(2): 19-22.]
[15] 蒋华兵, 李春丽, 陈强洪. 再入飞行器脉动压力环境特性分析[J]. 航天器环境工程, 2010, 27(3):378-382. [Jiang Hua-bing, Li Chun-li, Chen Qiang-hong. The characteristics of the fluctuating pressure environment for a re-entry vehicle [J]. Spacecraft Environment Technology, 2010, 27(3): 378-382.]
[16] 赵瑞, 荣吉利, 任方, 等. 火箭整流罩外气动噪声环境的大涡模拟研究[J]. 宇航学报, 2015, 36(9):988-994. [Zhao Rui, Rong Ji-li, Ren Fang, et al. Large eddy simulation of the aeroacoustic environment of a rocket fairing [J]. Journal of Astronautics, 2015, 36(9): 988-994.]
[17] Shen Y Q,Zha G G, Chen X Y. High order conservative differencing for viscous terms and the application to vortex-induced vibration flows [J]. Journal Computational Physics, 2008, 228(22):8283-8300.
[18] Dubuc L, Cantariti F, Woodgate M, et al. Solution of unsteady Euler equations using an implicit dual time step method [J]. AIAA Journal, 1998, 36(8): 1417-1424.
[19] Jameson A, Yoon S. Lower-upper implicit schemes with multiple grids for the Euler equations[J]. AIAA Journal, 1987, 25(7):929-935.
[20] 杨肖峰, 唐伟, 桂业伟. MSL火星探测器高超声速流场预测及气动性能分析[J]. 宇航学报, 2015, 36(4):384-389. [Yang Xiao-feng, Tang Wei, Gui Ye-wei. Hypersonic flow field prediction and aerodynamics analysis for MSL entry capsule [J]. Journal of Astronautics, 2015, 36(4): 384-389.]
[21] Anderson J D. Hypersonic and high-temperature gas dynamics[M]. Reston, Virginia: American Institute of Aeronautics and Astronautics, Inc. , 2006.
[22] Spalart P R, Allmaras S R. A one-equation turbulence model for aerodynamic flow [C]. The 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, Jan 6-9, 1992.
[23] Andersen B M, Whitmore S A. Aerodynamic control on a lunar return capsule using trim-flaps[C].The 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada,USA, Jan 8-11, 2007.
