利用地月间空间站的载人登月飞行模式分析
2018-06-04彭坤,杨雷
彭 坤,杨 雷
(中国空间技术研究院载人航天总体部,北京 100094)
0 引 言
载人登月飞行模式设计是载人登月工程实施须解决的关键问题之一。载人登月飞行模式是指飞行器根据载人登月任务需要分为不同的舱段完成不同的变轨任务,以降低整个飞行器的质量规模,同时依据运载火箭能力发射多个舱段在空间某个位置或轨道上进行交会对接和组装的方式。飞行模式决定了登月飞行器质量规模、火箭运载能力、任务可靠性、以及工程研制和实施风险。
早期载人登月飞行模式主要是直接往返探测模式,其研究重点集中在登月过程中空间交会对接轨道和次数的选择。载人登月飞行过程中比较稳定的近地轨道和环月轨道,一般作为登月飞行器组合体交会对接的场所。盛英华等[1]将火箭发射次数和对接次数限制在4次以内,分析了7种载人登月飞行模式。彭祺擘等[2]根据有无地球轨道和月球轨道交会对接,将飞行模式分为地球轨道交会-月球轨道交会、地球轨道交会-直接返回、地球轨道不交会-月球轨道交会、地球轨道不交会-月球轨道不交会4大类。根据阿波罗工程的经验,单一飞行器无法完成载人登月全部飞行任务,必须采用月面起飞后的环月轨道交会对接形式[3-4]。因此,月面直接返回的方式不可取。对于直接往返的载人登月飞行模式,可按照奔月过程中近地轨道和环月轨道的交会对接次数进行分类,包括直接奔月模式、近地轨道交会模式、环月轨道交会模式,近地轨道+环月轨道交会模式。阿波罗登月工程[5]采用的就是直接奔月模式,奔月过程中1次发射,没有近地轨道交会和环月轨道交会。2004年美国提出的重返月球的“星座”计划[6]充分考虑人员安全性和载人火箭研制难度,采用近地轨道1次交会的飞行模式,分别将载人飞船和月面着陆器发射到近地轨道进行交会对接,然后执行奔月任务。李桢等[7]采用的是奔月过程环月轨道交会的飞行模式。此外,NASA[8]于2004年分析过在地月L1和L2点交会的载人登月飞行模式。高启滨等[9]分析了基于地月L1点的载人登月飞行方案。
作为长期地外运行的载人空间设施,空间站可以为地月空间转移提供中转站。利用空间站进行载人登月任务,可以提高空间站的利用率,有效开发和利用地月空间经济圈;同时增加登月任务的灵活性,减少单次登月任务花费。1987年美国[10]提出基于近地轨道“自由号”空间站组装的登月方式。Thronson等[11]提出在地月L1点建立gateway空间站以支持载人月球探测和月球以远深空探测任务。Santovincenzo等[12]带领ESA论证组分析了基于近地轨道空间站和环月轨道空间站的载人登月飞行模式。彭祺擘[13]分析了基于我国近地轨道空间站的载人登月飞行模式,并进行了相应的奔月轨道及窗口设计。杨雷等[14]则创新性地提出了一种基于地月周期重访轨道空间站的载人月球探测飞行方案设想。
以上文献仅仅对不同轨道空间站的载人登月飞行模式进行了单独分析,目前还没有学者对基于地月空间内所有可行轨道空间站的载人登月飞行模式进行统一的优劣对比分析。基于此,本文首先设计了基于空间站的载人登月通用飞行方案,将基于空间站登月模式解耦为2个任务;其次通过各类型轨道设计和稳定性分析提出地月系统空间站可运行的飞行轨道或停泊点;而后详细分析6种可行轨道空间站的载人登月飞行模式的飞行方案、速度增量、飞行时间、空间环境、登月任务窗口、测控条件、交会对接任务难度、任务支持和任务可靠性;最后提出一套飞行模式定量评价方法对不同轨道空间站的载人登月飞行模式进行优劣综合评估,为未来开展基于空间站的载人月球探测任务设计提供参考。
1 基于空间站的载人登月任务分析
对于直接往返探测的飞行模式,其飞行过程各阶段互相关联,且受到登月点、任务窗口以及任务周期的严格约束。以“星座”计划的近地轨道1次对接飞行模式为例,其任务剖面如图1所示。该模式交会对接轨道选择为近地轨道,对接次数为1。
对于基于空间站的载人登月飞行模式,假设空间站已处于运营模式,空间站和月面着陆器已提前发送到指定轨道上,飞行过程从载人飞船发射开始,执行1次登月任务,直至返回地面。其任务剖面如图2所示。
与直接往返探测模式不同,空间站作为中转站,将载人登月任务分割为两部分(如图3所示):载人天地往返任务和登月任务。其中载人天地往返任务是指载人飞船在地面与空间站之间往返任务;登月任务是指月面着陆器在空间站与月面之间往返任务。空间站可以在载人登月过程中为航天员提供驻留平台,消除了任务周期约束。航天员乘坐载人飞船到达空间站后,可在空间站上等待合适登月窗口,再进行登月。同样,航天员完成登月任务返回空间站后,也可等待合适地球再入窗口再返回地球。因此,空间站将载人天地往返任务和登月任务完全解耦,增加了整个载人登月任务的灵活性,同时提高了任务可靠性和人员安全性。
2 地月间空间站运行轨道分析
基于空间站的载人登月飞行模式设计的核心是空间站运行轨道的选择,其直接影响载人登月任务的飞行方案和速度增量,以及空间站辐射环境和人员安全性。
按照距地球的远近顺序,地月空间主要存在近地轨道(Low Earth Oribt,LEO)、地球静止轨道(Geostationary Earth Orbit,GEO)、环月轨道(Circumlunar Orbit,CLO)、地月循环轨道(Earth-Lunar Cylcer Orbit,CYCLER)等稳定轨道(如图4所示),可作为空间站运行的备选轨道。同时地月系统5个平动点和平动点附近周期轨道也可作为空间站运行的停泊点和备选轨道。
2.1 中心引力体稳定轨道分析
中心引力体稳定轨道主要包括地球中心引力体稳定的LEO和GEO,以及月球中心引力体问题的CLO。
对于LEO,考虑到空间站长期运行,LEO轨道高度应远离大气层,从而降低轨道维持速度增量。LEO可采用国际空间站所处的400 km高度圆轨道。考虑登月任务需求,若采用轨道面内切向变轨进行地月转移加速,则为满足登月飞行器与任意赤纬的月球交会的条件,LEO的轨道倾角应大于月球轨道倾角[15]。月球轨道倾角变化范围是18°~28°[16],因此LEO轨道倾角可取为28°左右。
对于GEO,轨道高度为35 793 km,轨道倾角为0°,偏心率为0,其轨道参数已固定,唯一可变的是空间站所处星下点经度。每个月内月球赤纬为0°时刻为登月飞行器与月球的交会窗口。
对于CLO,轨道高度需综合考虑轨道维持和月面下降问题。CLO太低受月球非球形摄动影响大,轨道维持速度增量大;CLO太高,其月面下降所需速度增量大。阿波罗飞船环月飞行在100 km高度,考虑到轨道维持问题,CLO轨道高度范围取为300 km~500 km。该轨道高度较低,此范围内的CLO可称为低月球轨道(Low Lunar Orbit,LLO)。轨道倾角根据登月点经纬度决定。为满足登月任务要求,轨道倾角应大于登月点纬度。
2.2 CYCLER轨道分析
CYCLER轨道是指周期性往返于地球和月球之间,并在地球和月球附近绕飞而不停留的轨道。其本质是地月限制性三体问题下往返地月间的一类周期轨道[17]。考虑登月任务需求,地月循环轨道可采用共振型循环轨道,其近地点和近月点高度较低,且轨道周期与地月系统周期成固定比例。
本文选择与文献[14]相同的地月循环轨道,轨道周期约为14天,同时与月球会合的周期约为28天。由于地月周期重访特性,该轨道近似关于地月连线对称且处于月球轨道面内。文献[17]归纳了三种循环轨道的计算方法,设计过程相对复杂。本文根据CYCLER轨道的周期特性及共面特性,通过简单迭代直接在高精度动力学模型中设计一条CYCLER轨道,其轨道参数如表1所示。该轨道远地距约为48万千米,近地距约为1万千米。

表1 CYCLER轨道要素Table 1 CYCLER orbit elements
采用GMAT软件[18]对CYCLER轨道进行仿真,绘制其在1个月球会合周期内的飞行轨迹,如图5所示。从地心惯性系看,CYCLER轨道为绕地球长期稳定运行的大椭圆轨道。地月循环轨道的轨道周期约为14天,在约第7天位置与月球、地球共线。从地月旋转系看,其与月球会合的周期约为28天。在每28天内,一个14天周期与月球会合;另一个14天周期远离月球。
以表1参数为初值,用GMAT轨道推演10个轨道周期(140天),可得到CYCLER轨道地心距变化曲线,如图6所示。由图6可得,在10个轨道周期内,近地距变化范围为8 000 km~16 000 km,远地距变化范围为460 000 km~490 000 km,其近地距和远地距变化不大,验证了CYCLER轨道的运行稳定性。
2.3 地月平动点及其附近周期轨道分析
对于地月系统,采用圆型限制性三体模型来描述飞行器的运动,其会合系下归一化动力学方程如下[19]:
(1)
式中:
(2)
式中:m1和m2分别为地球和月球的质量。
所谓平动点,是飞行器在会合系中速度和加速度恒为零的位置,其数学表达式如下:
(3)
将上式代入圆型限制性三体问题的动力学方程可得地月系统5个平动点的位置,如图7所示。其中L1~L3位于地月连线上,称为共线平动点;L4~L5与地球和月球形成等边三角形,称为三角平动点。
由L3点的位置可知,其处在地月连线上,且位于地球一侧,远离月球。其登月飞行方案先要向L3飞行,然后再飞向月球,速度增量和飞行时间均比L1和L2点登月大,故一般不利用L3点地月空间站进行载人登月。由L4点和L5点的位置可知,登月飞行方案为先向L4点或L5点飞行,然后向月球飞行,相当于飞行2个地月距离。因此,L4点和L5点任务的飞行时间比L1和L2点任务长。同时,L4点和L5点为稳定平动点,其逃逸和制动速度比L1和L2点大。故不采用L4点和L5点地月空间站进行载人登月。因此,L1点和L2点比较适合作为空间站停泊点。
L2点始终位于月球背面,处在L2点的空间站与地球通信和测控会被月球挡住。为此,可将空间站置于L2点附近一定高度的Halo轨道上[20]。Halo轨道是平动点附近存在的一组周期轨道。本文计算出一条地月L2点附近振幅Az=8000 km的Halo轨道作为空间站运行轨道,其三视图如图8所示。
除Halo轨道外,L2点还存在Lyapunov周期轨道,其属于二维轨道,只存在地月旋转系XY平面内,无Z轴分量,如图9所示。由图9可知,Lyapunov轨道靠近地月连线附近仍然会被月球遮挡。
此外,还存在一类绕月球逆行的平面轨道DRO[21](Distant Retrograde Orbit,大幅值逆行轨道),其具有Lyapunov稳定性,轨道维持速度增量小,如图10所示。当DRO幅值减小会逐渐退化为环月轨道。由于其同样存在于地月平面内,仍存在被月球遮挡问题。
综上所述,对于地月平动点空间站飞行模式,主要考虑L1点空间站飞行模式和L2点Halo轨道空间站飞行模式。
3 基于不同轨道空间站的登月飞行模式
针对上一节得到的6种空间站可运行轨道和停泊点,从载人登月任务的飞行方案和速度增量需求、空间站环境和安全性、登月任务窗口、测控可见性、技术难度、后续任务支持和任务可靠性等方面全面分析不同位置空间站登月模式的优缺点。
由于空间站将登月任务和载人天地往返任务解耦,登月任务不用考虑载人天地往返任务中地面发射到空间站的窗口,仅考虑空间站到登月点的窗口。因此,本文所说的登月窗口特指空间站到月面的窗口。
为便于比较各模式飞行方案和速度增量,将不同轨道空间站的载人登月飞行过程统一分为7个阶段:(1)地面到LEO飞行阶段;(2)LEO到空间站飞行段;(3)空间站到LLO飞行段;(4)LLO到月面飞行段;(5)月面到LLO飞行段;(6)LLO到空间站飞行段;(7)空间站到地面飞行段。
3.1 基于LEO空间站的登月飞行模式
该模式飞行方案如图11所示。不考虑火箭发射载人飞船至LEO的速度增量,单纯比较登月飞行器的速度增量,则载人登月过程可分为6个变轨子阶段,如表2所示。其中LLO返回空间站过程中采用化学推进制动方式,其速度增量约3.2 km/s。LEO到LEO空间站可采用快速交会对接,时间为6小时。参考阿波罗工程,地月转移时间3天。
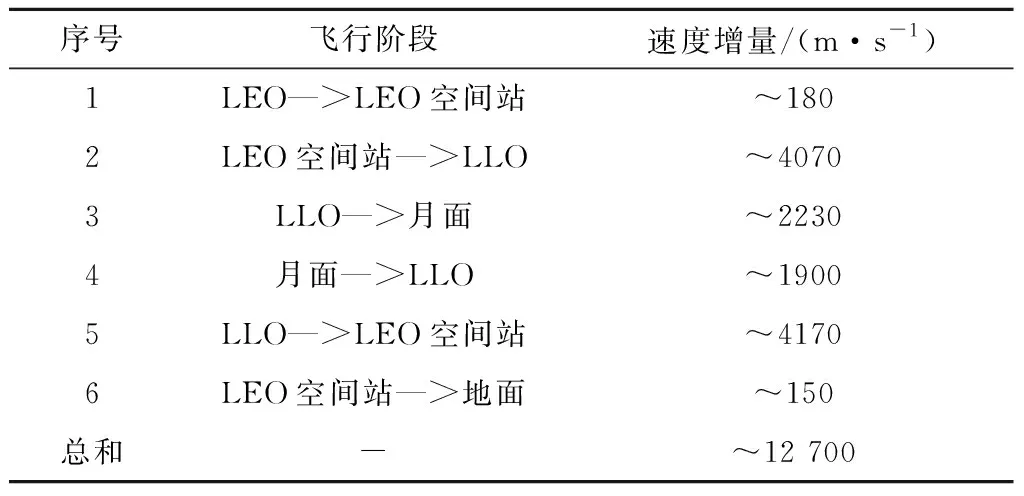
表2 基于LEO空间站登月飞行模式速度增量需求Table 2 Velocity increment of Lunar mission flight mode based on LEO space station
LEO存在大气阻力、空间碎片撞击概率相对较大。空间辐射环境好,不会遭遇地球辐射带带电粒子,太阳宇宙射线和银河宇宙射线影响较小[22]。空间热环境不稳定,交替变化。由于LEO空间位置一定,其每月与月球轨道的交点为2个,即每月有2次登月窗口。测控站主要考虑近地测控站、深空站以及中继卫星,测控系统与空间站不是连续可见,每圈近地轨道不可见时间约15min。该模式主要涉及2次LEO交会对接,第1次交会对接与现有LEO交会对接相近,技术比较成熟。第2次交会对接为返回LEO交会对接,其难度主要体现在从月地转移轨道到LEO进行近地制动的精度。在后续任务支持方面,可支持一定纬度区域的登月任务以及LEO范围内的科学研究,小行星和火星探测任务逃逸速度大。该模式交会对接、飞行控制和测控通信技术难度低,空间环境稳定,综合任务可靠性高。
3.2 基于GEO空间站的登月飞行模式
基于GEO空间站的登月飞行方案如图12所示。登月飞行器速度增量需求如表3所示。其中LEO到GEO空间站转移按照先近地点提升远地点高度,再在远地点变轨道面和圆化变轨的方式,速度增量较大,飞行时间预留2天。

表3 基于GEO空间站登月飞行模式速度增量需求Table 3 Velocity increment of Lunar mission flight mode based on GEO space station
GEO可不计大气阻力;空间辐射环境较近地恶劣,处于外辐射带,将遭遇辐射带捕获电子;其空间碎片撞击概率较大;热环境稳定。由于空间站的GEO空间位置一定,每月有2次登月窗口。测控系统与GEO空间站连续可见。该模式涉及2次GEO交会对接,第1次交会对接可通过LEO向GEO转移进行调相和调平面,技术难度较低;第2次交会对接的难点是返回GEO的近地制动精度。在后续任务支持方面,登月任务所需速度增量较大,可进行GEO范围内的科学研究,小行星和火星探测任务逃逸速度较大。该模式交会对接、飞行控制和测控通信技术难度较低,空间环境较稳定,综合任务可靠性较高。
3.3 基于CYCLER空间站的登月飞行模式
基于CYCLER空间站的登月飞行方案如图13所示。通过增大LEO到CYCLER和LLO到CYCLER的往返时间,可降低其转移速度增量。其中,LEO到CYCLER飞行时间取为7天。考虑到CYCLER仅有8天左右时间靠近月球,LLO到CYCLER转移时间不能过长,可取为4天。登月飞行器速度增量需求如表4所示。

表4 基于CYCLER空间站登月飞行模式速度增量需求Table 4 Velocity increment of Lunar mission flight mode based on CYCLER space station
CYCLER不存在大气、光照条件良好、热环境稳定、但微流星撞击概率较大。空间辐射环境恶劣,将反复穿越外辐射带,期间将遭遇辐射带捕获电子;地月间持续遭遇银河宇宙射线和太阳风粒子,太阳宇宙射线只有处于太阳爆发期间才考虑。CYCLER每28天内与月球会合一次,其登月窗口为每月1次。测控系统与空间站连续可见。该模式涉及地球大椭圆轨道交会对接,登月飞行器通过2次脉冲变轨进入空间站附近区域,进行自主控制段飞行并完成对接。其难度主要体现在2次脉冲变轨的精度,登月飞行器的自主导航和控制精度,大椭圆轨道运行轨道各点速度的不一致性。在后续任务支持方面,可支持全月面登月任务以及整个地月空间的科学研究,小行星和火星探测任务逃逸速度较小。该模式交会对接技术难度高,空间环境恶劣,综合任务可靠性低。
3.4 基于L1点空间站的登月飞行模式
基于L1点空间站的登月飞行方案图14所示。考虑载人因素,LEO到L1点往返时间为4天,L1点到LLO往返时间为3天。登月飞行器速度增量需求[8]如表5所示。

表5 基于L1点空间站登月飞行模式速度增量需求Table 5 Velocity increment of Lunar mission flight mode based on L1 point space station
L1点空间环境与CYCLER相近,不同之处在于L1点空间站不需要穿越地球辐射带,辐射环境较好。在地月旋转系中L1点相对月球的位置固定不变,故其随时可以登月。L1点始终处在地月连线之间,故地面3个深空站和2颗中继卫星可保持对L1点空间站的不间断测控通信。该模式涉及地月空间平动点交会对接,登月飞行器通过2次脉冲变轨进入L1点附近区域,再进行自主控制飞行最终完成对接。由于空间站处于L1点,故交会对接不需相位调整;同时L1点处于力平衡位置,自主控制速度增量消耗小。其难度主要体现在深空飞行的导航精度和登月飞行器的自主导航和控制精度。在后续任务支持方面,可支持全月面登月任务以及地月L1点的科学研究,小行星和火星探测任务逃逸速度较小。该模式交会对接难度较高、深空弱稳定场飞行控制技术难度高,空间环境较稳定,综合任务可靠性较低。
3.5 基于L2点Halo轨道空间站的登月飞行模式
基于L2点Halo轨道空间站的登月飞行方案如图15所示。与L1点空间站登月飞行方案略有不同,基于L2点Halo轨道空间站的登月飞行方案中采用月球借力方式去L2点Halo轨道,以减小轨道转移的速度增量[23-24]。由于增加月球借力,LEO到L2点Halo往返时间增至8天。
考虑载人因素,L2点到LLO往返时间为3天。登月飞行器速度增量需求[8, 23-24]如表6所示。
L2点Halo轨道空间环境与L1点类似,由于其处于月球外侧,微流星撞击概率相对较大。在地月旋转系中L2点Halo轨道相对月球的位置固定不变,从地月L2点Halo轨道所有相位点都可转移到某近月点[24],即从地月L2点Halo轨道空间站随时可以登月,但Halo轨道不同相位登月的速度增量不同,最差点相对最优点相差约300 m/s。由于L2点Halo轨道有一定的轨道高度,能避免被月球遮挡,可以与地面3个深空站和2颗中继卫星进行测控通信。该模式涉及地月空间平动点Halo轨道交会对接,登月飞行器通过轨道转移进入L2点Halo轨道附近区域,进行自主控制段飞行并完成对接。其难度主要体现在Halo轨道进入精度,Halo轨道进入相位,以及登月飞行器的自主导航和控制精度。其总体交会对接难度略大于L1点交会对接。在后续任务支持方面,可支持全月面登月任务,月球背面通信,以及地月L2点的科学研究,小行星和火星探测任务逃逸速度小。L2点Halo轨道的不变流形可延伸到深空,是支持载人深空探测任务最理想的驻留平台。该模式交会对接和飞行控制技术难度、以及空间环境与L1点空间站模式类似,综合任务可靠性较低。
3.6 基于LLO空间站的登月飞行模式
基于LLO空间站的登月飞行方案如图16所示。与直接往返模式类似,区别在于LLO上多了1个空间站,载人飞船和月面着陆器通过空间站进行人员和货物的转移。奔月过程中载人飞船与LLO空间站的交会对接预留2天时间。登月飞行器速度增量需求与近地轨道+环月轨道对接的直接往返模式速度增量相同,如表7所示。

表7 基于LLO空间站登月飞行模式速度增量需求Table 7 Velocity increment of Lunar mission flight mode based on LLO space station
LLO无大气、热环境变化较大(受月球红外辐射影响),微流星撞击概率比L1点大,空间辐射环境与L1点类似。LLO始终围绕月球转动,其登月窗口主要考虑LLO星下点是否经过登月点。对于环月极轨道,半个月可遍历全月面,即登月窗口为每半个月1次。测控系统与空间站不是连续可见,每圈环月轨道不可见时间约为44 min。该模式涉及2次LLO交会对接。第1次交会对接是奔月过程LLO交会对接,其难度主要体现在环月轨道进入精度,远程导引测定轨精度等。第2次交会对接为Apollo工程中月面上升后的LLO交会对接,技术难度相对较小。在后续任务支持方面,可支持全月面登月任务以及LLO的科学研究,小行星和火星探测任务逃逸速度较大。该模式交会对接、飞行控制和测控通信技术难度中等,空间环境较差,综合任务可靠性中等。
3.7 各飞行模式对比分析
各飞行模式对比分析如表8所示。其中飞行时间不计月面任务时间和空间站停泊时间,仅计算载人飞船和月面着陆器往返空间站的时间。由于采用LEO快速交会对接,LEO空间站登月模式飞行时间最短;CYCLER和L2点Halo轨道空间站登月模式飞行时间最长。LEO和GEO空间站登月模式的速度增量远大于其它轨道模式。原因在于载人飞船返回空间站时需要大速度增量制动,而其它模式中载人飞船直接返回地面,通过再入大气减速。
相对于L1和L2点Halo空间站,LLO空间站登月模式登月窗口较少,测控条件差,空间环境较差,对深空探测任务支持小;CYCLER空间站登月模式登月窗口少,交会对接难度大,空间环境较差。
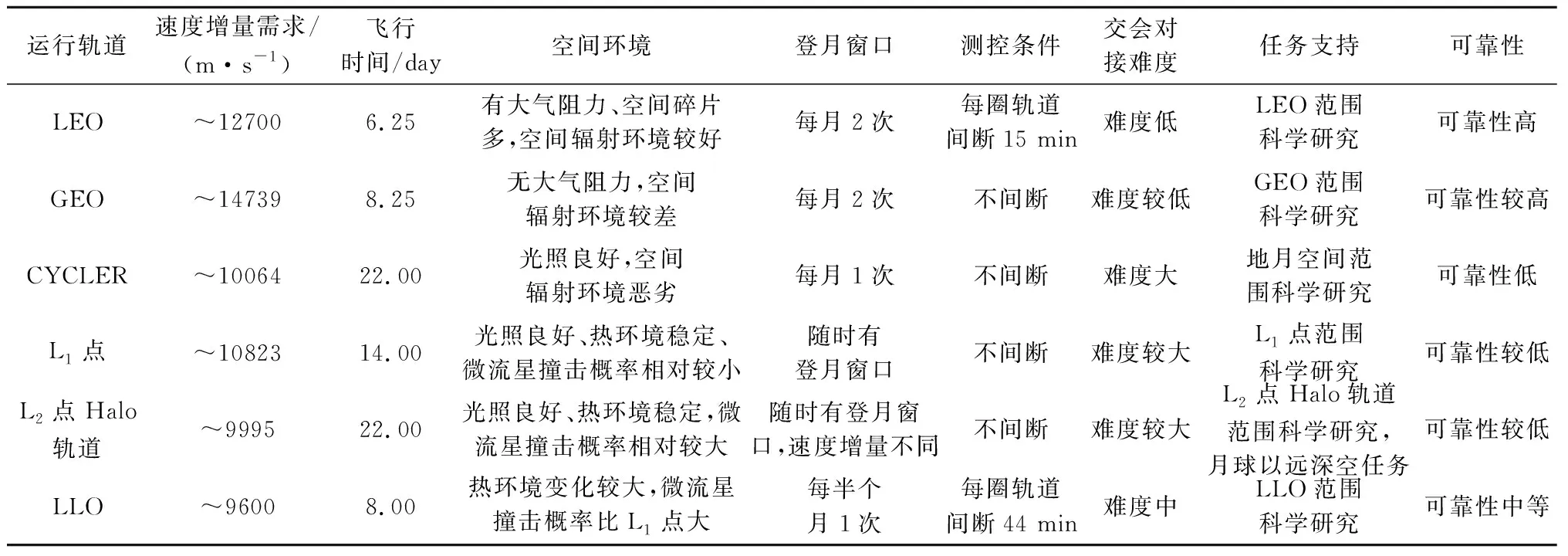
表8 基于不同轨道空间站的登月飞行模式优劣比较Table 8 Advantages and disadvantages of lunar mission flight mode based on different orbit space station
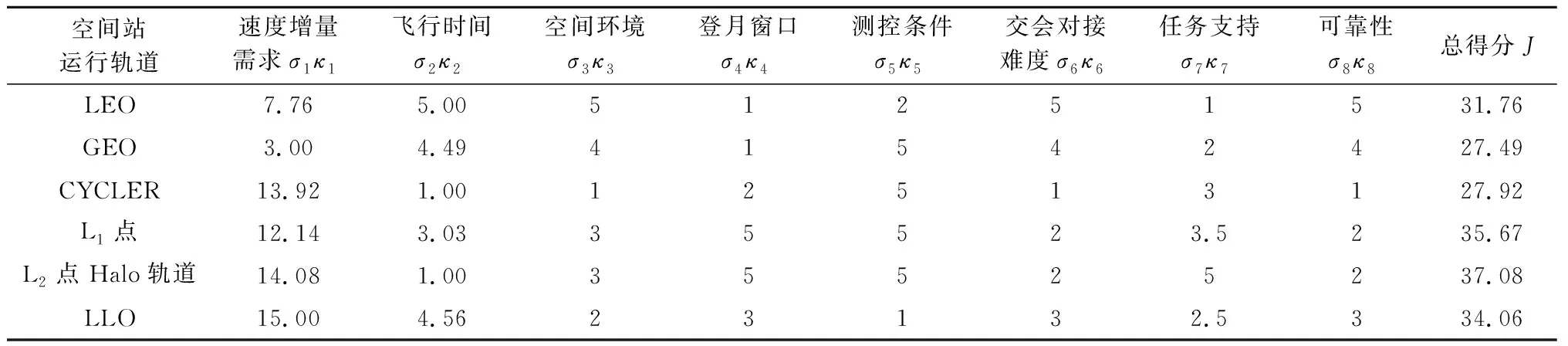
表9 基于不同轨道空间站的登月飞行模式定量评价Table 9 Quantitative evalunation of lunar mission flight mode based on different orbit space station
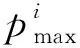
(4)
飞行模式综合评价指标公式如式(5)所示。
(5)
式中:σi为各评估要素的权重系数。对于载人登月任务,速度增量需求直接决定任务可行性和飞行器规模,需要重点考虑,同时权重太低不足以反映速度增量的差距,故取σ1=3。其它权重均取为1。采用此评价模型对6种飞行模式进行评估,各项评价要素得分和总得分如表9所示。
由表9可得6种飞行模式的得分高低顺序是L2点Halo轨道>L1点>LLO>LEO>CYCLER>GEO。因此,L1点和L2点Halo轨道空间站的登月飞行模式为较优的飞行模式。与L1点空间站登月模式相比,L2点Halo轨道空间站登月模式虽然飞行时间较长,但总速度增量需求更小,可以支持月球背面测控,以及更好地支持载人小行星和火星等深空探测任务,其综合优势更大。
4 结 论
对于基于地月间空间站的载人登月飞行模式,GEO空间站登月模式总速度增量需求较大;CYCLER空间站登月模式登月窗口少,空间环境较差;LLO空间站登月模式总速度增量小,登月窗口较少,测控条件和空间环境差;LEO空间站技术成熟度高,可实现性最强,但其总速度增量需求较大,若采用大气辅助变轨等方式减少返回LEO空间站的制动速度增量,可作为可行登月飞行模式。L1点和L2点Halo轨道空间站登月模式登月窗口多,支持全月面登月任务。其中,L2点Halo轨道空间站登月模式速度增量需求更小,可支持月球背面测控通信并能更好支持载人深空探测任务。为便于定量评估各模式优劣,本文建立一套数学模型进行综合评估,L2点Halo轨道空间站登月模式得分最高,是优选的登月飞行模式。
为便于比较,本文仅考虑地月空间设置一处空间站的情况,后续工作可考虑在两个或多个不同轨道或停泊点设置空间站组合的登月飞行模式;此外,CLO仅分析了LLO,可详细分析其它轨道高度的CLO,综合分析其优劣。
参 考 文 献
[1] 盛英华,张晓东,梁建国,等. 载人登月飞行模式研究[J]. 宇航学报,2009, 30(1): 1-7. [Sheng Ying-hua, Zhang Xiao-dong, Liang Jian-guo, et al. A study of the human lunar exploration mission modes[J]. Journal of Astronautics, 2009, 30(1): 1-7.]
[2] 彭祺擘,李桢,李海阳. 载人登月飞行方案研究[J]. 上海航天,2012, 29(5): 14-19. [Peng Qi-bo, Li Zhen, Li Hai-yang. Analysis on manned lunar mission flight mode[J]. Aerospace Shanghai, 2012, 29(5): 14-19.]
[3] Logsdon J M, Launius R D. Human spacefligh: projects Mercury, Gemini, and Apollo[M]. Washington, DC: NASA History Division Office of External Relations, 2008
[4] 李成智,李建华. 阿波罗登月计划研究[M]. 北京:北京航空航天大学出版社,2009.
[5] Low G M. Apollo 11 mission report[R]. MSC-00171, Houston, Texas: Manned Spacecraft Center, November 1969.
[6] NASA. NASA’s exploration systems architecture study[R]. NASA-TM-2005-214062, November 2005
[7] 李桢,周建平,程文科,等. 环月轨道交会的奔月方案[J]. 国防科技大学学报,2009, 31(1): 16-20. [Li Zhen, Zhou Jian-ping, Cheng Wen-ke, et al. Investigation on lunar mission based on lunar orbit rendezvous[J]. Journal of National University of Defense Technology, 2009, 31(1): 16-20.]
[8] Robertson E, Geffre J, Joosten K, et al. Lunar architecture focused trade study final report[R]. ESMD-RQ-0005, Washington, DC: NASA, 22 October 2004
[9] 高启滨,张洪礼,韩潮. 基于地月L1点的载人登月飞行方案分析[J]. 载人航天,2014,20(6): 562-568. [Gao Qi-bin, Zhang Hong-li, Han Chao. Flight scheme of manned lunar landing mission based on the first earth-lunar lagrangian point(L1)[J]. Manned Spaceflight, 2014, 20(6): 562-568.]
[10] Llewellyn C P, Brender K D. Technology development,demonstration and orbital support requirements for manned lunar and mars missions[R]. NASA Technical Memorandum 101666, 1990
[11] Thronson H, Geffre J, Prusha S, et al. The lunar L1 gateway concept: supporting future major space science facilities[R]. NASA-20040074295, March 2002
[12] Santovincenzo A, Thomas U, Khna M, et al. Architecture study for sustainable lunar exploration[R]. CDF Study Report: CDF-33(A), December, 2004
[13] 彭祺擘. 基于空间站支持的载人登月方案研究[D]. 长沙: 国防科学技术大学,2007. [Peng Qi-bo. The scheme study of manned lunar-landing mission supported by space station[D]. Changsha: National University of Defense Technology, 2007.]
[14] 杨雷,向开恒,童科伟,等. 基于地月周期重访轨道空间站的载人月球探测方案设想[J]. 载人航天,2013, 19(5): 47-51. [Yang Lei, Xiang Kai-heng, Tong Ke-wei, et al. A manned lunar exploration system architecture based on earth-moon cycler orbit space station[J]. Manned Spaceflight, 2013, 19(5): 47-51.]
[15] Peng K, Yim S Y, Zhang B N, et al. Fast search algorithm of high-precision earth-moon free-return trajectory[C]. 2015 AAS/AIAA Astrodynamics Specialist Conference, Vail, Colorado, USA, August 10-13, 2015
[16] 郗晓宁,曾国强,任萱等. 月球探测器轨道设计[M]. 北京:国防工业出版社,2001.
[17] 张文博,成跃,王宁飞. 地月循环轨道动力学建模与计算研究[J]. 宇航学报,2015, 36(5): 510-517. [Zhang Wen-bo, Cheng Yue, Wang Ning-fei. Dynamics modeling and calculation of cycler trajectories in the Earth-Moon system[J]. Journal of Astronautics, 2015, 36(5): 510-517.]
[18] Hughes P S, Qureshi H R, Cooley D S, et al. Verification and validation of the general mission analysis tool(GMAT)[C]. 2014 AIAA/AAS Astrodynamics Specialist Conference, San Diego, CA, USA, August 5-7, 2014
[19] 彭坤,李明涛,王平,等. 基于不变流行的地月L2点Halo轨道转移轨道设计[J]. 载人航天,2016, 22(6): 673-679. [Peng Kun, Li Ming-tao, Wang Ping, et al. Transfer trajectory design for EML2 halo orbit based on invariant manifolds[J]. Manned Spaceflight, 2016, 22(6): 673-679.]
[20] Farquhar R W. Lunar communications with libration-point satellites[J]. Journal of Spacecraft and Rockets, 1967, 4(10): 1383-1384
[21] Demeyer J, Gurfil P. Transfer to distant retrograde orbits using manifold theory[J]. Journal of Guidance Control and Dynamics, 2007, 30(5): 1261-1267
[22] 李春来,欧阳自远,都亨. 空间碎片与空间环境[J]. 第四纪研究,2002,22(6): 540-551. [Li Chun-lai, Ouyang Zi-yuan, Du Heng. Space debris and space environment[J]. Quaternary Sciences, 2002, 22(6): 540-551.]
[23] Burns J O, Kring D A, Hopkins J B, et al. A lunar L2-farside exploration and science mission concept with the Orion multi-purpose crew vehicle and a teleoperated lander/rover[J]. Advances in Space Research, 2013, 52(2): 306-320
[24] Hopkins J B. Proposed orbits and trajectories for human missons to the Earth-Moon L2 region[C]. 64th International Astronautical Congress, Beijing, China, September 23-27, 2013
