冗余空间机械臂抓捕自旋卫星后的消旋控制

王明明，罗建军，余 敏，袁建平

(1. 西北工业大学航天飞行动力学技术重点实验室，西安 710072;2. 西北工业大学深圳研究院，深圳 518057)

0 引 言

随着卫星维护、在轨装配和空间碎片移除等任务需求的与日俱增，我们期望利用空间机器人去执行特殊恶劣空间环境下的任务。典型实例有“Robot Technology Experiment(ROTEX)”，“Engineering Test Satellite VII(ETS-VII)”，“轨道快车(Orbit Express, OE)”和“Robonaut 2”等[3]。空间机器人在轨服务中最具挑战性的工作之一是抓捕后阶段的消旋。抓捕后阶段的目的是消除目标卫星的旋转运动，同步稳定基座。因此，针对目标卫星的消旋问题必须研究特定规划与控制方法。

文献中已提出过多种空间机器人轨迹规划和运动控制方法。基于零作用空间(Reaction Null-Space, RNS)的概念，Yoshida等人[1]提出了无反作用机械臂，解决了运动学非冗余臂和冗余臂时间损失和机械臂速度限制的问题。此外，文献[2]中也采用了基于RNS的轨迹规划方法，根据动量守恒定律实现了抓捕自旋目标。文献[3]中给出对目标卫星自主抓捕与服务的框架。之后，Xu等人[4]利用自由漂浮空间机器人非完整特性提出了一种点到点的路径规划方法，同时调节基座姿态和末端的位姿。Lampariello等人[5]研究了一种机器人最优抓捕机动目标的实时轨迹规划方法，利用B样条参数化期望的关节轨迹，采用序列二次规划方法搜索最优解[6]。羊等人[7]针对自由漂浮空间机器人末端轨迹跟踪优化控制中惯性参数不确定问题，提出一种组合优化控制方法，实现了系统跟踪的能量优化，同时保证了对期望末端轨迹的有效跟踪。文献[8]中应用Bézier曲线规划关节轨迹，采用粒子群优化方法求解最优化问题。郭等人[9]分析了利用空间机器人抓捕目标卫星时产生的碰撞问题，并基于粒子群算法给出了最优碰撞前构型。此外，结合RNS和动力学平衡控制的概念，Wang等人[10]提出一种基于任务优先级的运动学冗余机械臂路径规划方法。文献[11]结合命题逻辑理论和模型预测控制方法，解决了空间机器人在含有障碍物工作空间中的最优控制问题。针对空间机器人的运动控制问题，考虑到动力学不确定特性，Xu等人[12]提出了一种针对自由飞行机器人的自适应控制方法。Matsuno和Saito等人[13]引入了一种协调和输入转换算法，将含漂移项的仿射系统转换成时间状态控制项。此后，文献[14]提出了一种考虑避撞的非线性模型预测控制方法，实现了末端的路径跟踪控制。近年来，多自由度机械臂的控制中，也可采用滑模控制[15]及鲁棒精确控制[16]等。

前文所提的研究大都是抓捕前的轨迹规划与运动控制。当机械臂抓捕一个不可控的卫星后，应使目标尽可能快速停靠，即通过机械臂逐步对目标施加力矩，消除二者间的相对速度。然而，针对最优消旋运动规划的研究却很少。针对抓捕后阶段，文献[17]中提出了一种基于RNS概念的机械臂控制方法，将基座的角动量传到机械臂，减小了关节角速度。Yoshida等人[18]提出了一种分布式动量控制方法，保证对基座姿态干扰最小情况下将目标角动量传到反作用轮。文献[19]提出了一种自由漂浮空间机器人抓捕翻滚目标存在模型不确定性时的阻抗控制方法。罗等人[20]针对抓捕后的动力学参数辨识问题，提出一种参数辨识的持续激励轨迹设计方法，提高了空间机器人参数辨识的收敛速度并保证其准确性。然而，这些工作中没有研究最优路径规划方法和基座姿态稳定。基于庞特里亚金极小值原理，文献[21]中提出一种机械臂先拦截非合作目标卫星再消旋的方法，主要考虑消旋时间最少。考虑了初末边界条件的不确定性，Abad等人[22]设计了一种减小对基座姿态干扰的最优控制方法。针对空间机器人抓捕大惯量目标的情形，Zhang等人[23]提出了一种基于自适应滑模控制方法的协同稳定技术。如何消除目标的旋转运动是未来在轨服务的关键技术之一。迄今为止，设计机械臂的消旋策略仍是一个具有挑战性的问题。

本文旨在提出一种利用运动学冗余臂抓捕非合作目标的新消旋策略。由于运动学冗余臂存在多解，利用此特性可以满足多种约束条件。考虑简洁性和规范化因素，选择Bézier曲线规划抓捕后目标的路径。此外，利用自适应DE算法搜索最优消旋时间和目标的终端位姿，并生成末端的参考消旋轨迹。本文推导了一种同时稳定基座和末端的协调控制方法，主要贡献是针对运动学冗余空间机器人抓捕自旋卫星后阶段，设计了最优消旋策略和协调控制方法。

本文组织如下：第1节介绍了抓捕后阶段组合体系统的多体动力学。基于最优化理论，第2节推导了利用四阶Bézier曲线和自适应DE算法的路径规划与消旋策略。第3节给出了消旋过程中协调控制基座姿态和机械臂末端的闭环解。第4节展示了所提消旋策略与协调控制方法应用于运动学冗余空间机器人的仿真结果。最后，第5节给出结论。

1 抓捕后动力学建模

机器人系统由基座和n自由度的机械臂构成，共计n+1个部件。抓捕后阶段，机器人和目标卫星连接成一个组合体，如图1所示。由文献[21]，根据拉格朗日力学原理，空间机器人动力学方程表示如下：

表1 本文所用运动学和动力学符号Table 1 Kinematic and dynamic symbols used in the paper

(1)

目标卫星的动力学方程表示如下：

(2)

式中：mt和It分别是目标卫星的质量和惯性张量。抓捕矩阵Jte表示如下：

(3)

参考式(2)，由机械臂施加的力和力矩fe可写成：

(4)

在抓捕后阶段，末端与抓捕点速度和加速度关系建立如下：

(5)

(6)

(7)

将式(4)和式(7)代入式(1)，消除fe项，可得组合体系统的动力学方程：

(8)

2 消旋策略

利用欧拉方程建立目标卫星姿态动力学：

(9)

参考文献[21],假设通过参数辨识方法可得到目标的惯性参数It。在抓捕前阶段，合理假设目标卫星不受任何合外力和力矩，即τt=0而且ft=0。

·在可行域内优化特定的目标；

·保证末端执行器路径的连续性；

·尽量减小运动过程中不期望的影响。

2.1 消旋轨迹参数化

(10)

(11)

(12)

(13)

(14)

(15)

(16)

给定目标的终端状态φf，通过式(10)～(13)可解得仅含单个变量T的目标消旋轨迹。参考式(16)，在给定的约束下，利用二分搜索法可确定最优消旋时间T：

T≥max{Ti=min(fi1(T)≥0∩fi2(T)≥0)}，i=1,2,3

(17)

实际上，不仅要考虑最优消旋时间，施加于目标的控制力矩也要尽量减小。因此，优化过程中，定义目标函数如下，

(18)

ω1,ω2>0分别是最优时间和控制力矩的权重因子。

定义设计变量φf，消旋策略可转化为：

(19)

如上所述，采用四阶Bézier曲线，消旋策略最终转化为以φf为设计变量的优化问题。根据目标自旋运动的初始状态确定搜索域[φmin,φmax]。一旦确定φf，则可解算出最优消旋时间T和目标消旋运动。推导出末端执行器的期望轨迹如下：

(20)

(21)

式中：Rt(φ)是从目标体坐标系到惯性系的坐标转换矩阵，Euler2quat(φ)函数将以欧拉角形式表示的姿态转化为以四元数形式表示。

2.2 微分进化算法

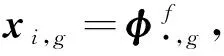
(22)

式中：rand(0,1)是[0,1]中生成的随机数。xj,min和xj,max分别是变量xj的下界、上界。

初始化后采取突变策略，生成目标向量xi,g对应的突变向量vi,g=(vi1,g,vi2,g,…,vid,g)。突变方法包括DE/rand/1、DE/best/2、DE/current-to-best/1等。xbest,g是当前整体中的最佳个体。接下来，vi,g和xi,g之间进行交叉操作，生成新试验向量ui,g=(ui1,g,ui2,g,…,uid,g)。通常DE算法采用二项式交叉策略。交叉后，针对试验向量ui,g评估式(18)中所示的目标函数。根据贪心算法，只有当ui,g越优，才能选择xi,g作为幸存的子代。

DE算法重复进行上述操作生成新一代个体，直到满足终端标准。如[25]所述，贪心算法可能会导致过早收敛、置信度低，自适应参数机制有助于提高进化种群的多样性和算法的鲁棒性。参考文献[26]，在第g代迭代中，个体xi,g的缩放因子Fi和交叉速率Gi通过自适应参数机制生成。自适应机制的目的是记录近期有效参数Fi和Gi，以构建好的参数引导生成子代。完成迭代后，自适应DE算法将给出T*和p*的最优解。参考式(20)和(21)，确定末端执行器消除目标自旋运动的期望轨迹。

3 协调控制

(23)

(24)

(25)

注意式(25)阐明了追踪星与目标组合体关于其在任务空间的动力学方程。实际上，在抓捕后阶段保持基座姿态的稳定十分重要，因为：1)需要保持基座上测量仪器和扫描设备的指向；2)在消旋过程中减小碰撞的风险。本文中，不考虑基座位移变化，即不对基座施加控制力而考虑对基座姿态进行稳定。广义力输入us表示如下：

(26)

为推导简化形式的动力学方程(33)，定义如下：

(27)

式中：D11∈R3×3，c1∈R3。可得以下方程：

(28)

(29)

(30)

(31)

(32)

式中：K.p，K.d分别表示位姿和速度的反馈增益，均为正定矩阵。采用单位四元数q={η,ε}∈R4设计协调控制方法(η是四元数中标量部分，ε是其矢量部分)。q1与q2的四元数误差计算如下，其中⊗是四元数乘法符号：

(33)

(34)

(35)

(36)

(37)

代入四元数误差，计算V关于时间的导数：

(38)

4 仿真结果

为了验证所提消旋策略和协调控制方法的实用性，本节给出了采用运动学冗余机械臂抓捕自旋目标的演示实例。如图1和图5所示，追踪星有6DOF，其机械臂包含7DOF。表2中列出空间机器人的运动学和动力学参数，其中ai，bi和Ii均表示在其本体坐标系下。

4.1 最优时间和终端状态确定

空间机器人抓捕目标卫星的典型过程可粗略地分为抓捕前和抓捕后两个阶段：抓捕前，机械臂从初始位置接近目标上的抓捕点，捕获目标时相对速度最小从而实现最小碰撞。抓捕点为ρtg=[-0.35,0,0.4275] m。抓捕后，机械臂需要在给定的约束下实现目标的消旋与稳定。本文主要关注抓捕后阶段的消旋策略和控制方法。图6给出了抓捕前末端执行器和抓捕点的轨迹。

基座杆1杆2杆3杆4杆5杆6杆7目标m/kg2004.08.02.06.02.02.05.020.0Ixx500.30.80.10.70.10.10.48.4Iyy1000.30.50.10.40.10.10.112.18Izz1000.20.80.10.70.10.10.212.84ax/m0.00.00.00.00.00.00.00.0ay/m0.00.0-0.70.0-0.50.00.00.0az/m0.00.1280.0840.090.0840.090.0840.12bx/m0.90.00.00.00.00.00.00.0by/m0.0840.084-0.66-0.084-0.460.084-0.090.0bz/m-0.60.1280.00.00.00.00.00.21

标和空间机器人的状态如下：

(39)

本文中，搜索算法采用带有自适应缩放因子和交叉概率的突变方法，即DE/current-to-best/1。每次迭代中，利用DE算法先确定最优消旋时间T，然后利用适应度函数优化目标的终端状态，生成相应的消旋路径。DE算法涉及的参数分别设置为np=10，c=0.5。smax=100是最大迭代次数，作为DE算法的终止条件。

基于给定的初始状态，如式(39)，DE算法成功地搜索获得满足所有约束的最优解T*=4 s，p*=(0.1226,-0.0119,6.725×10-3)。如图7所示，最佳适应度函数的收敛性与迭代次数呈负相关，适应度值的快速递减显示了DE算法的搜索能力。就搜索的最优解p*和消旋时间T*而言，图8给出了抓捕点的期望运动规律和所需控制力矩。可以看出，通过设计的消旋策略，目标在预设的约束下可成功地实现消旋稳定。

4.2 协调控制仿真

5 结 论

在抓捕后阶段，为了尽快使非合作目标卫星稳定，并考虑控制力矩约束，本文给出了一种空间机器人最优消旋策略和协调控制方法。首先，基于广义速度推导了运动学冗余空间机器人抓捕非合作目标卫星后的动力学方程。然后，采用四阶Bézier曲线规划消旋轨迹，利用带自适应缩放因子和交叉概率的DE算法搜索给定约束条件下的最优终端状态，优化过程中同时考虑消旋时间和控制力矩最优。最后，研究了一种在消除了目标的自旋运动的同时稳定基座姿态的协调控制方法。仿真结果表明本文所提消旋策略和协调控制器的可行性和有效性。

参 考 文 献

[1] Yoshida K, Hashizume K, Abiko S. Zeros reaction maneuver: flight validation with ets-vii space robot and extension to kinematically redundant arm[C]. Proceedings of the 2001 IEEE International Conference on Robotics and Automation, Seoul, Korea, May 21-26, 2001.

[2] Shah S V, Sharf I, Misra A. Reactionless path planning strategies for capture of tumbling objects in space using a dual-arm robotic system[C]. Proceedings of AIAA Guidance, Navigation, and Control Conference, Boston, MA, Aug 19-22, 2013.

[3] Rouleau G, Rekleitis I, L′Archeveque R, et al. Autonomous capture of a tumbling satellite[C]. IEEE International Conference on Robotics and Automation, Roma, Italy, April 10-14, 2007.

[4] Xu W F, Li C, Wang X, et al. Study on non-holonomic cartesian path planning of a free-floating space robotic system [J]. Advanced Robot, 2009, 23(1-2): 113-143.

[5] Lampariello R, Tuong D, Castellini C, et al. Trajectory planning for optimal robot catching in real-time[C]. Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, May 9-13, 2011.

[6] Nanos K, Papadopoulos E. Avoiding dynamic singularities in cartesian motions of free-floating manipulators [J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(3): 2305-2318.

[7] 羊帆, 张国良, 原磊,等. 自由漂浮空间机器人末端轨迹优化跟踪控制[J]. 宇航学报, 2016, 37(7):846-853. [Yang Fan, Zhang Guo-liang, Yuan Lei, et al. End-effector optimal tracking control of free-floating space robot [J]. Journal of Astronautica, 2016, 37(7):846-853.]

[8] Wang M M, Luo J J, Walter U. Trajectory planning of free-floating space robot using particle swarm optimization (pso) [J]. Acta Astronautica, 2015, 112: 77-88.

[9] 郭闻昊, 王天舒. 空间机器人抓捕目标星碰撞前构型优化[J]. 宇航学报, 2015, 36(4):390-396. [Guo Wen-hao, Wang Tian-shu. Pre-impact configuration optimization for a space robot capturing target satellite [J]. Journal of Astronautica, 2015, 36(4):390-396.]

[10] Wang M M, Luo J J, Walter U. Novel synthesis method for minimizing attitude disturbance of the free-floating space robots [J]. Journal of Guidance, Control, and Dynamics, 2016, 39 (3): 695-704.

[11] 宗立军, 罗建军, 王明明,等. 自由漂浮空间机器人多约束混合整数预测控制[J]. 宇航学报, 2016, 37(8):992-1000.[Zong Li-jun, Luo Jian-jun, Wang Ming-ming. A mixed integer predictive controller with multi-constraint for free-floating space robots [J]. Journal of Astronautica, 2016, 37(8):992-1000.]

[12] Xu Y, Shum H Y, Lee J J, et al. Adaptive control of space robot system with an attitude controlled base[C]. Proceedings 1992 IEEE International Conference on Robotics and Automation, Nice, France, May 12-14, 1992.

[13] Matsuno F, Saito K. Attitude control of a space robot with initial angular momentum[C]. Proceedings 2001 IEEE International Conference on Robotics and Automation, Seoul, Korea, May 21-26, 2001.

[14] Wang M M, Luo J J, Walter U. A non-linear model predictive controller with obstacles avoidance for a space robot [J]. Advances in Space Research, 2016, 57: 1737-1746.

[15] Zadeh H, Mohammad S, Saeed K, et al. Optimal sliding mode control of a robot manipulator under uncertainty using pso [J]. Nonlinear Dynamics, 2016, 84(4): 2227-2239.

[16] Wei C S, Luo J J, Dai H H, et al. Globally robust explicit model predictive control of constrained systems exploiting svm-based approximation [J]. International Journal of Robust and Nonlinear Control, 2016.

[17] Nenchev D N, Yoshida K. Impact analysis and post-impact motion control issues of a free-floating space robot subject to a force impulse [J]. IEEE Transactions on Robotics and Automation, 1999, 15(3): 548-557.

[18] Yoshida K, Dimitrov D, Nakanishi H. On the capture of tumbling satellite by a space robot[C]. Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, Oct 9-15, 2006.

[19] Abiko S, Lampariello R, Hirzinger G. Impedance control for a free-floating robot in the grasping of a tumbling target with parameter uncertainty[C]. IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, Oct 9-15, 2006.

[20] 罗建军, 薛爽爽, 马卫华,等. 空间机器人抓捕目标后动力学参数辨识研究[J]. 宇航学报, 2016, 37(12):1411-1418. [Luo Jian-jun, Xue Shuang-shuang, Ma Wei-hua, et al. Dynamic parameter identification of free-floating space robots after capturing targets [J]. Journal of Astronautica, 2016, 37(12):1411-1418.]

[21] Aghili F. A prediction and motion-planning scheme for visually guided robotic capturing of free-floating tumbling objects with uncertain dynamics [J]. IEEE Transactions on Robotics, 2012, 28(3): 634-649.

[22] Flores-Abad A, Wei Z, Ma O, et al. Optimal control of space robots for capturing a tumbling object with uncertainties [J]. Journal of Guidance, Control, and Dynamics, 2014, 37(6): 2014-2017.

[23] Zhang B, Liang B, Wang Z, et al. Coordinated stabilization for space robot after capturing a noncooperative target with large inertia [J]. Acta Astronautica , 2017, 134: 75-84.

[24] Storn R, Price K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces [J]. Journal of Global Optimization, 1997, 11 (4): 341-359.

[25] Piotrowski A. Review of differential evolution population size [J]. Swarm and Evolutionary Computation, 2017, 32: 1-24.

[26] Zhang J, Sanderson A C. JADE: adaptive differential evolution with optional external archive [J]. IEEE Transactions on Evolutionary Computation, 2009, 13 (5): 945-958.

[27] Siciliano B, Sciavicco L, Villani L, et al, Robotics Modelling, Planning and Control[M]. 1st Edition, Springer, London, 2009.