平面向量求解中的误区警示
2018-06-04李佳宁
■李佳宁
平面向量融数、形于一体,具有几何与代数的“双重身份”,它是沟通代数、几何与三角函数的一种工具,有着极其丰富的实际背景。下面汇集了求解向量问题中的种种错误,并剖析其原因,希望对大家的学习有所帮助。
误区1:忽视向量概念中的特殊情况
例 1下列四个命题,其中正确命题的个数为( )。
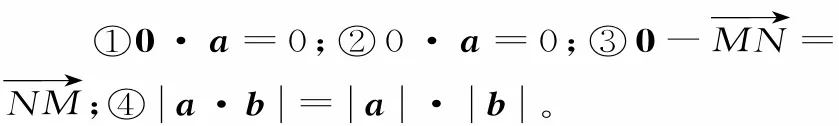
A.1 B.2
C.3 D.4
错解:四个命题都正确,应选D。
剖析:根据向量数量积的概念,可知0·a应是一个实数0,0·a应是一个向量0,①正确,②错误。由向量的减法运算法则和向量共线的意义,可知③正确。由 a·b =a ·b cosθ ,可知当θ=0或θ=π时,a·b =a ·b成立,④错误。应选B。
警示:求解有关向量问题,一定要注意向量的本质属性,分清特殊情况和一般成立的关系,注意零向量和实数0的区别。
变式训练1:下列命题正确的是( )。
A.a∥b,b∥c⇒a∥c
B.若a与b互为相反向量,则a+b=0
C.平面向量a,b平行的充要条件是存在不全为0的实数λ1,λ2,使得λ1a+λ2b=0
D.若a与b互为相反向量,则a≠b
提示:当b=0时,A错误。互为相反向量的和为零向量而不是实数0,B错误。当a=0时,其相反向量也是0,此时a=b,D错误。应选C。
误区2:忽视两个向量的夹角
例 2在△ABC中,a=5,b=8,C=60°,则的值为( )。
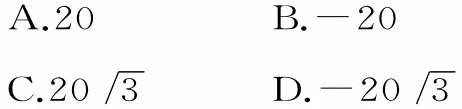

警示:利用向量可以平移的特点,将两个向量平移为共起点的两个向量,再求两个向量的夹角。两个向量a与b的夹角公式为量a与b的夹角。
变式训练2:若非零向量a,b满足|a|=,且 (a - b)⊥ (3a +2b),则向量a与b夹角的正弦值为( )。

误区3:忽视一个向量在另一个向量方向上的投影
例 3已知向量a,b的夹角为45°,且b在a方向上的投影等于( )。

剖析:上述解法忽视了向量b在a方向上的投影的意义,错解求的是向量a在b方向上的投影。
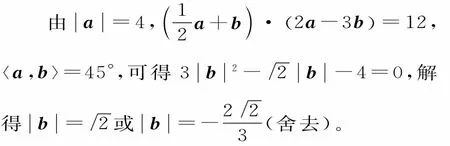
故向量b在a方向上的投影等于
警示:若向量a=(x1,y1),b=(x2,y2),〈a,b〉=θ,则向量a在b方向上的投影为问题的两个注意点:①向量a在b方向上的投影是有序的;②向量a在b方向上的投影是一个数量,可正,可负,可为零。
变式训练3:已知点A(-1,1),B(1,2),C(-2,-1),D(3,4),则向量AB→在CD→方向上的投影为( )。

误区4:忽视向量数量积与实数乘法的区别
例 4已知a,b都是非零向量,且向量a+3b与7a-5b垂直,向量a-4b与7a-2b垂直,求向量a与b的夹角。
错解:由题意可得方程组:
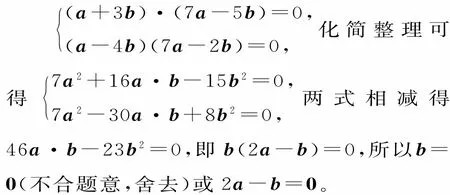
由2a-b=0,可知a与b同向,故向量a与b的夹角为0°。
剖析:对于实数a,b,若a b=0,则a=0或b=0,但对于向量a,b,若满足a·b=0,则不一定有a=0或b=0,因为a·b=|a|·|b|cosθ与θ有关,当θ=90°时,a·b=0恒成立,此时a,b均可以不为0。
把b2=2a·b代入7a2+16a·b-15b2=0,得a2=2a·b。
故a2=b2=2a·b,则cos〈a,b〉=可得〈a,b〉=60°,即向量a与b的夹角为60°。
警示:向量的数量积运算不满足结合律,也不满足消去律,解题时要引起大家的注意。
变式训练4:以下四个命题,其中正确命题的个数为( )。
① (a · b)·c=a·(b · c);②|a+b|≤a +b;③ (a - b)·c=a·c-b·c;④如果a·b=a·c,且a≠0,那么向量b,c在a方向上的投影相等。
A.1 B.2
C.3 D.4
提示:向量的数量积的运算不满足结合律,①错误。由向量几何运算的意义及平行四边形法则,可知②正确。由向量的运算法则,可知③正确。a·b=a·c,说明b,c在a方向上的投影相等,④正确。应选B。
误区5:误认为向量a与b的夹角为钝角(锐角)⇔a·b<0(>0)
例 5已知a=(2,1),b=(λ,1),λ∈R,a与b的夹角为θ。若θ为锐角,则λ的取值范围是( )。

剖析:上述解法忽视了向量的夹角与向量的数量积的关系。当θ为锐角时,应满足0<cosθ<1,而错解中没有排除cosθ=1,即两向量共线且同向的情况。

警示:一般地,向量a,b为非零向量,a与b的夹角为θ,则〈a,b〉为锐角⇔a·b>0为钝角⇔a·b<0且a与b不共线⇔
变式训练5:已知a=(1,2),b=(1,1),且a与a+λ b的夹角为锐角,则实数λ的取值范围为( )。
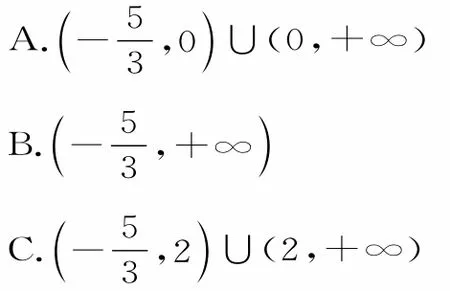
提示:由题意得a·(a+λ b)>0,且a与a+λ b的夹角不等于0°。

误区6:忽视共线向量或三点共线的条件
例 6已知同一平面上的向量a,b,c两两所成的角相等,且|a|=1,|b|=2,|c|=3,求向量a+b+c的长度。
错解:易知a,b,c均为非零向量。
设a,b,c所成的角均为θ,则3θ=360°,即θ=120°。
所以a·b=|a|·|b|cos 120°=-1。
同理可得,b·c=-3,c·a=-。
由|a+b+c|2=a2+b2+c2+2a·b+2b·c+2c·a=3,可得|a+b+c|=。
剖析:上述解法是把a,b,c看成非共线向量求解的,而当a,b,c共线且同向时,它们所成的角都相等且等于0°,也符合题意。
当向量a,b,c共线且同向时,它们所成的角均为0°,这时|a+b+c|=|a|+|b|+|c|=6;
当向量a,b,c不共线时,由错解可知|a+b+c|=。
综上所述,向量a+b+c的长度为6或
警示:求解共线向量问题时,一定要注意向量 的 方 向。 若(λ,μ 为常数),则A,B,C三点共线的充要条件是λ+μ=1。
变式训练6:如图1,在△ABC中,AD=DB,AE=EC,CD与BE交于点F,已知=x a+y b,则(x,y)为( )。
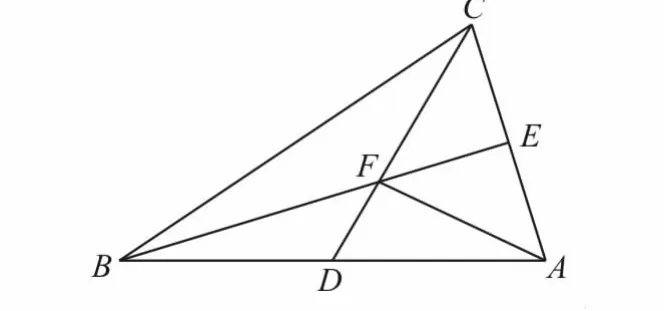
图1

误区7:忽视向量的几何意义与三角形“内心”之间的关系
例 7设O是平面上一定点,A,B,C是平面上不共线的三个点,动点P满足P的轨迹一定经过△ABC的( )。
A.外心 B.内心
C.重心 D.垂心
错解:应选A或C或D。
剖析:上述解法忽视了共起点的两个单位向量的和向量为其角平分线,而△ABC的角平分线的交点为内心,题设中的动点P 满点P的轨迹一定经过△ABC的内心。应选B。
警示:由两个单位向量的和向量以及向量共线的条件可得:若P经过△ABC的内心。
变式训练7:已知△ABC的三个内角A,B,C所对边的长分别为a,b,c,M 为该三角形所在平面内的一点,若a=0,则点M是△ABC的( )。
A.内心 B.重心
C.垂心 D.外心
提示:如图2,延长CM 交AB于点D。
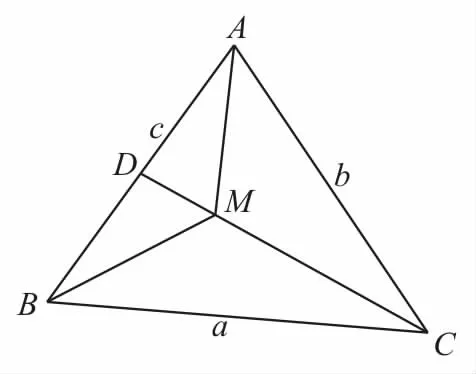
图2

由三角形的内角平分线定理的逆定理可得CD为∠ACB的平分线。
同理可证,AM、BM 的延长线也是角平分线。
故M是△ABC的内心。应选A。
误区8:忽略向量的几何意义与三角形“垂心”之间的关系
例8已知O是平面上的一定点,A,B,C是平面上不共线的三个点,动点P满足λ∈(0,+∞),则动点P 的轨迹一定经过△ABC的( )。
A.重心 B.垂心
C.外心 D.内心

A.垂心 B.重心
C.内心 D.外心

故点O是△ABC的垂心。应选A。
误区9:忽略向量的几何意义与三角形“外心”之间的关系
例 9已知O是平面上的一定点,A,B,C是平面上不共线的三个点,动点P满足λ∈(0,+∞),则动点P 的轨迹一定经过△ABC的( )。
A.外心 B.内心
C.重心 D.垂心
错解:应选B或C或D。

A.外心 B.内心
C.重心 D.垂心

