平面向量综合演练A卷
2018-06-04吴传叶
■吴传叶
一、选择题
1.已知a,b是不共线的向量=λ a+b=a+μb,λ,μ∈R,则A,B,C三点共线满足的条件是( )。
A.λ+μ=2 B.λ-μ=1
C.λμ=-1D.λμ=1
2.如图1,平行四边形ABCD中,E,F分别是BC,CD的中点,DE交AF于点H,记=( )。
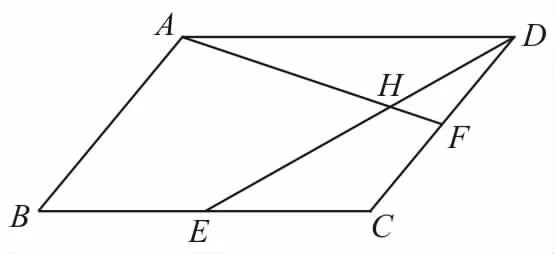
图1
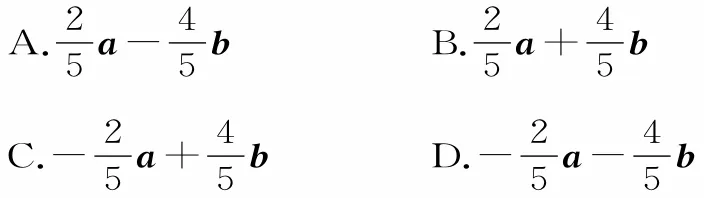
3.已知O,A,B,C为同一平面内的四个点,若满足2=0,则向量等于( )。
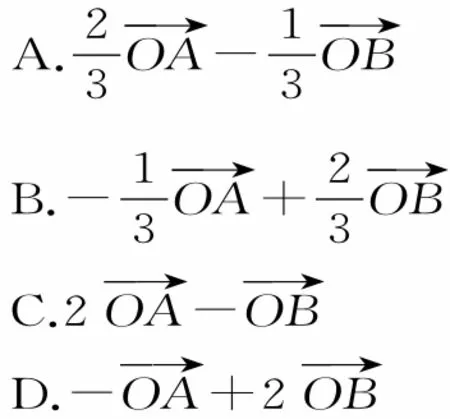
4.在四边形ABCD中=a+2b,=-5a-3b,则四边形ABCD是( )。
A.矩形 B.平行四边形
C.梯形 D.以上都不对
5.已知向量a,b,c中任意两个都不共线,但a+b与c共线,b+c与a共线,则向量a+b+c=( )。
A.a B.b
C.c D.0
6.设D,E,F分别是△ABC的边BC,CA,AB上的点,且
A.反向平行
B.同向平行
C.互相垂直
D.既不平行也不垂直
7.若点M 是△ABC所在平面内的一点,且满足5,则△ABM与△ABC的面积的比为( )。

9.若向量a,b不共线,则下列各组向量中,可以作为一组基底的是( )。
A.a-2b与-a+2b
B.3a-5b与6a-10b
C.a-2b与5a+7b
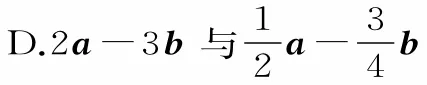
10.如图2,在△O AB中,P 为线段AB上的一点,则( )。
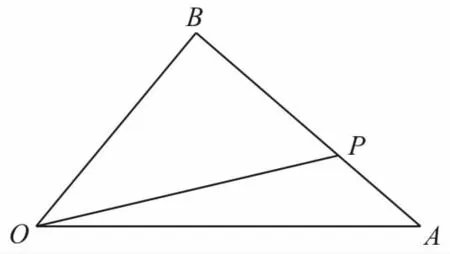
图2


12.已知点 M(5,-6)和向量a=(1,-2),若向量=-3a,则点N的坐标为( )。
A.(2,0) B.(-3,6)
C.(6,2) D.(-2,0)
13.已知向量=(k,12),=(4,5),=(-k,10),且A,B,C三点共线,则k的值是( )。

14.在平行四边形ABCD中=(2,8),=(-3,4),对角线AC与BD相交于点M,则=( )。
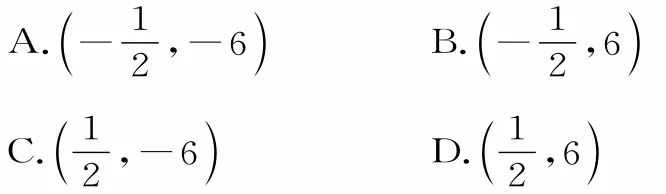
15.设向量a=(1,-3),b=(-2,4),c=(-1,-2),若表示向量4a,4b-2c,2(ac),d的有向线段首尾相连能构成四边形,则向量d=( )。
A.(2,6) B.(-2,6)
C.(2,-6) D.(-2,-6)
16.在平面直角坐标系x O y中,已知点A(1,0),B(0,1),C为第一象限内的一点,且λ+μ=( )。

17.若向量a,b 满足|a|=1,(a+b)⊥a,(2a+b)⊥b,则|b|=( )。

18.已知|a|=1,|b|=2,c=a+b,且c⊥a,则向量a与b的夹角为( )。
A.30° B.60°
C.120° D.150°
19.已知向量a=,1),b=(0,1),c=(k,),若向量a+2b与c垂直,则k=( )。
A.-3 B.-2
C.1 D.-1
20.在平面直角坐标系x O y中,已知四边形ABCD是平行四边形=(1,-2),=( )。
A.5 B.4
C.3 D.2
21.若平面向量a=(-1,2)与b的夹角是180°,且|b|=3,则向量b的坐标为( )。
A.(3,-6) B.(-3,6)
C.(6,-3) D.(-6,3)
22.如图3,已知△ABC是边长为1的等边三角形,点D,E分别是边AB,BC的中点,连接DE并延长到点F,使DE=2EF,则的值为( )。
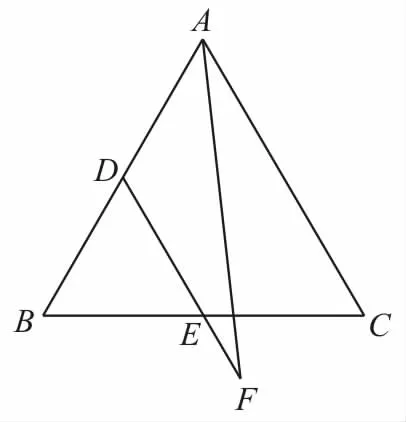
图3

23.已知△ABC为等边三角形,AB=2,设点P,Q满 足=(1-λ)·,则 实 数 λ=( )。
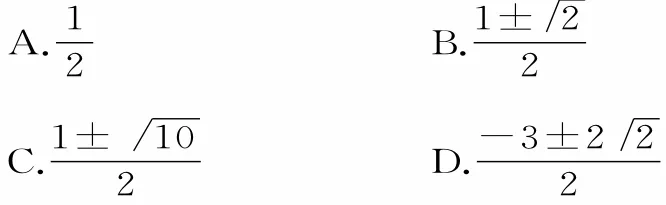
二、填空题
24.已知向量a=(λ,2λ),b=(3λ,2),如果向量a与b的夹角为锐角,则λ的取值范围是____。
25.如图4所示,菱形ABCD的边长为2,∠BAD=60°,M 为DC的中点,若N 为菱形内任意点(含边界),则的最大值为____。
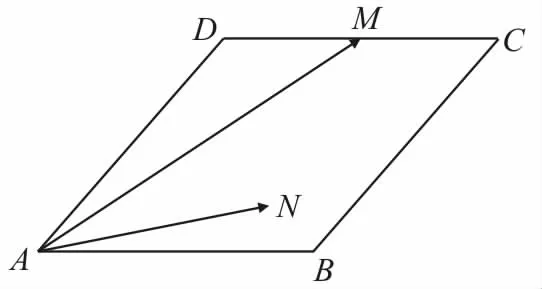
图4
26.已知向量a与b为两个不共线的单位向量,k为实数,若向量a+b与向量k ab垂直,则k=。

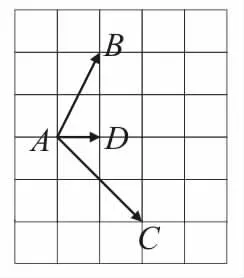
图5
29.已知 P={a|a=(-1,1)+m(1,2),m∈R},Q={b|b=(1,-2)+n(2,3),n∈R}是两个向量集合,则集合P∩Q 等于。


三、解答题
35.有下列命题:①已知a,b是平面内两个非零向量,则平面内任一向量c都可表示为λ a+μb,其中λ,μ∈R;②对平面内任意四边形ABCD,若点E,F分别为AB,CD的中点,则2;③已知向量a=(1,-1),A,B为直线x-y-2=0上的任意两点,则向量AB→∥a;④已知向量a与b的夹角-1;⑤由a∥c,可得(a·b)·c=a·(b·c)。其中正确的是____(写出所有正确命题的编号)。

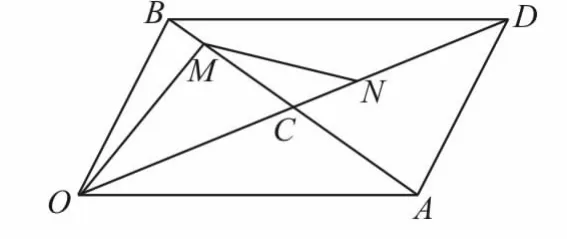
图6

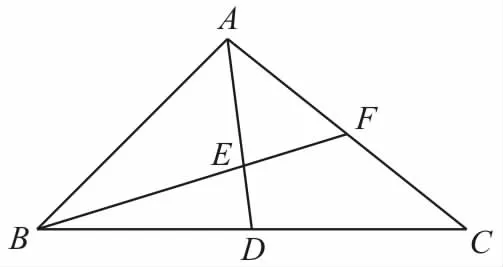
图7
(1)用a,b表示向量
(2)求证:B,E,F三点共线。
39.已知|a|=4,|b|=3,(2a-3b)·(2a+b)=61。
(1)求向量a与b的夹角θ的大小。
(2)求|a+b|的值。
(3)若=b,求△ABC的面积。
