聚焦20 17年高考中的平面向量问题

■张启兆 陈伟斌

平面向量是高中数学的重要内容，它集“数”“形”于一体，是沟通代数与几何的桥梁。高考主要考查向量的基本概念及基本运算，其中对向量的线性运算、坐标运算、数量积运算的考查尤为突出，同时也注重考查向量与其他知识的交汇问题。下面从20 17年高考的平面向量试题中选取典型题目，剖析高考中此类问题的命题方向和考查目标，希望对同学们的学习有所帮助。

一、向量的线性运算

例 1 (20 17年高考天津卷改编)已知D为△ABC所在平面内的一点，若=则( )。

评注：在△ABC中是平面向量的减法运算法则，熟练掌握这一运算法则有助于快速解题。

二、向量的坐标运算

例2(20 17年高考山东卷改编)已知向量a=(2，6)，b=(-1，3λ)，若a∥b，则λ=____。

解：由a∥b，可得-1×6=6λ⇒λ=-1。

评注：向量的坐标运算是向量中最简单、最基本的运算，它把向量的几何运算转化为代数运算，是以“数”解“形”的典型例证。本题主要考查了向量平行与向量的坐标运算。解答本题的关键是要熟记两向量平行的坐标表示。

例3(20 17年高考新课标卷改编)已知向量a=(-1，2)，b=(7m，1)。若向量a+b与a垂直，则m=____。

解：由题意得a+b=(7m -1，3)。

由a+b⊥a，可得 (a + b)·a=0，所以-(7m -1)+2×3=0，解得m=1。

评注：解答本题的关键是要熟记向量垂直的坐标表示。

三、向量的模

例4(20 17年高考新课标卷改编)已知向量a，b的夹角为30°，|a|=2，|b|=3，则|a+2b|=____。

评注：在向量模的计算中，求平方是常用且有效的方法，通过平方以及利用向量数量积等知识将向量的模转化为实数问题来研究。

四、向量的数量积

例5(20 17年高考新课标卷改编)已知三角形ABC是边长为2的等边三角形，P为三角形ABC所在平面内一点，则2的最小值是( )。

解：如图1，以BC的中点D为坐标原点，BC所在直线为x轴，建立平面直角坐标系x Dy，则点B(-1，0)，C(1，0)，A(0，3)。

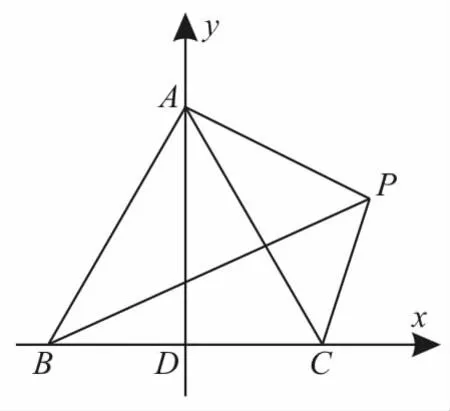
图1

设点P(x，y)，则=(-x，-y)，(-1-x，-y)，=(1-x，-y)，

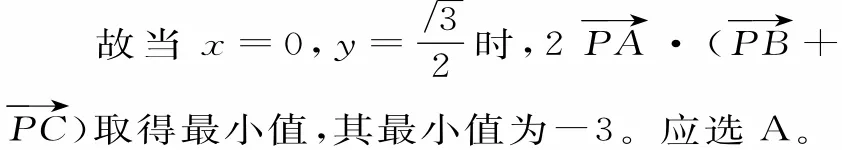
评注：抓住问题的特点，建立适当的坐标系，利用坐标法解决向量问题是一种重要的解题手段。求解向量的数量积问题有“三法”：定义法、坐标法、基底法。本题也可以用定义法和基底法来求解。向量的数量积有两种表现形式：一是已知两个向量的模和夹角求数量积，二是已知两个向量的坐标求数量积。

评注：本题是利用“算两次”的思想方法求解的。解题时，通过向量的模与向量运算的灵活转换，应用平面向量的夹角公式，建立方程求得λ的值。

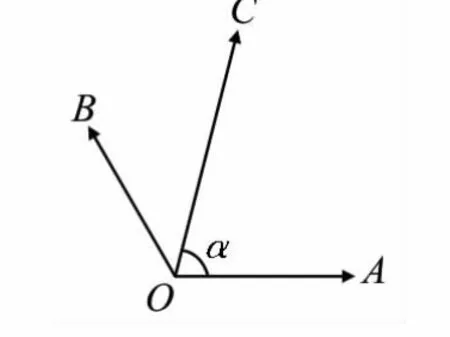
图2

五、平面向量的基本定理

例 8(20 17年高考天津卷)如图3，在△ABC中，∠A=60°，AB=3，AC=2。若(λ∈R)，且=-4，则λ 的值为 。

图3

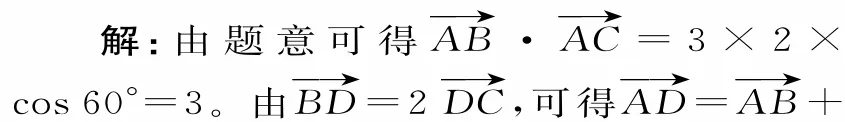
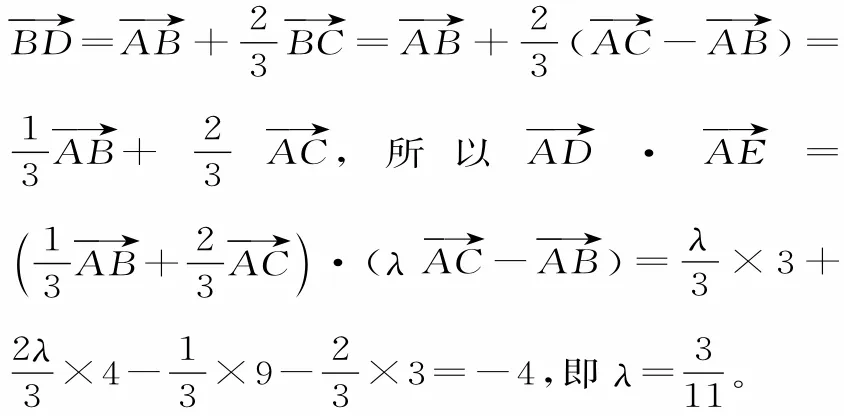
评注：解答本题时，选取基底很重要。题中向量的模和夹角已知，选作基底易于计算数量积。

例 9(20 17年高考新课标卷)如图4，在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上。若则λ+μ的最大值为( )。

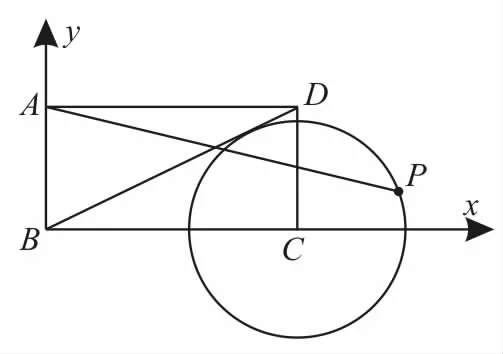
图4

解：由图4可建立直角坐标系x By，则点A0，1()，B0，0()，C2，0()，D2，1()，P x，y()。

评注：应用平面向量基本定理表示向量的实质是利用向量的平行四边形法则或三角形法则进行向量的加、减或数乘运算。用向量基本定理解决问题的一般思路是：先选择一组基底，并运用该基底将条件和结论表示成向量的形式，再通过向量的运算来解决问题。

六、平面向量与三角函数的交汇

例 10(20 17年高考江苏卷)已知向量a=(cosx，sinx)，b=(3，-)，x∈[0，π]。

(1)若a∥b，求x的值。

(2)记f(x)=a·b，求f(x)的最大值和最小值以及对应的x的值。

解：(1)因为a=(cosx，sinx)，b=(3，-)，a∥b，所以-cosx=3sinx。

若cosx=0，则sinx=0，这时与sin2x+cos2x=1矛盾，故cosx≠0，于是可得

评注：向量与三角函数的交汇问题，通常有向量与解三角形相结合的问题，也有向量与三角函数图像平移相结合的问题，考查的难度属于中等偏易。