用心倾听题目的声音
——以一道几何作图题的破解为例
2018-06-01周卫花
周卫花
(浙江省台州市黄岩区东浦中学 318020)
南京师范大学教授单墫在《解题研究》中说:“解题是数学学习的中心,学习数学就是学会解题.”现在重要的考试如中考、高考都是以题目为载体来考察学生各方面的掌握情况,而在无声的考场上有一种声音最可靠,那就是题目的声音,只有用心倾听题目的声音才能正确地分析问题解决问题.
为了检测我校九年级学生寒假在家的学习情况,学校组织了开学检测,其中有一道几何作图题得分很低,这引发了我们备课组几位老师的热烈讨论,一致认为指导学生用心倾听题目的声音是破解问题的关键.
一、题目呈现
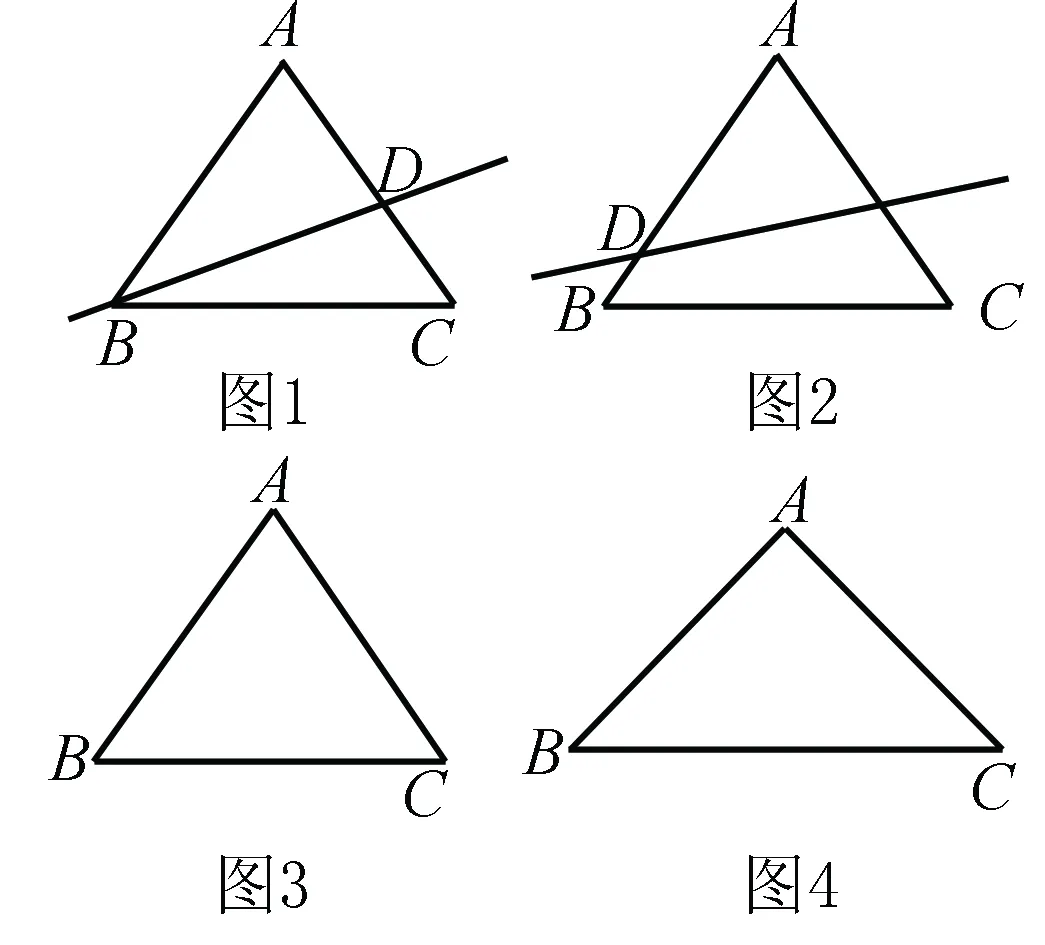
定义:如果一条直线既等分三角形的周长,又等分该三角形的面积,我们称这条直线为三角形的“等分周积线”.例如:如图1,在△ABC中,若AB+AD=BC+CD,且S△ABD=S△BCD,则直线BD为△ABC的“等分周积线”.如图2,在△ABC中,若AD+AE=DB+BC+CE,且S△ADE=S四边形DBCE,则直线DE为△ABC的“等分周积线”.
请你解答下列问题: (1)如图3,在△ABC中,AB=AC,且BC≠AC,请你在图3中用尺规作图作出过点A的△ABC的“等分周积线”;(2)如图4,在△ABC中,AB=AC=m,BC=n,且m 解法评析这种作法是在第(1)小题的基础上寻求解题方法,在数学解题时我们有时要关注小题之间的关联性,学会利用前面小题的结论解决后面小题,有时还可以从特殊情况着手,寻求一般的解决问题的方法,从特殊到一般是一种重要的解决数学问题的方法. 解法评析这个作法是通过构造基本图形从而解决问题,在数学解题时有时识记一些基本图形有助于我们在掌握基础知识的前提下快捷地形成解题思路. 基础知识是解题最基本的工具.若学生对某个基础知识存在缺陷,在解题时就会因为基础知识的不扎实,基本方法不熟练而影响对相关知识的摄取和灵活运用,从而导致解题受阻.因此在平时教学中教师应对核心的知识落实到位,既要注重对基础知识源的理解与构建,更要注重对相关知识源的综合与整理.同时也要关注每个学生存在的知识缺陷,以免形成“缺陷积累”. 基本图形是几何概念的源泉,也是几何定理的表形.在几何教学上重视基本图形教学,教会学生从复杂的图形中分解出基本图形,成为几何教学比较有效的突破口,也成为学生化被动为主动的突破口.有时抓住基本图形就能找到破解的方法.因此在平时的教学和学习中都要积累基本图形,这能有助于快速的解决问题. 波利亚认为在解决问题的四个环节(弄清问题、拟定计划、实现计划和回顾)中认为最重要的是“回顾”.只有深刻回顾题目中蕴涵的数学思想方法,知识才能内化为能力,并能在新的题目中迁移运用.在教学中我们应给学生说出自己想法的机会.从多角度去深化对问题的理解,优化学生的思维路径,总结归纳一般的解题策略.方能再听到题目所发出的各种声音,达到举一反三的效果.从而培养学生反思意识,形成反思习惯,成为善于认识和解决问题的人才. 参考文献: [1]韦丽云.基于核心素养的初中几何入门教学实践探究[J].中学数学教学参考,2017(11). [2]严惠.对初中数学“图形与几何”的教学研究[J].上海中学数学,2017(06).二、破解之法
1. 用心倾听,从特殊情况着手

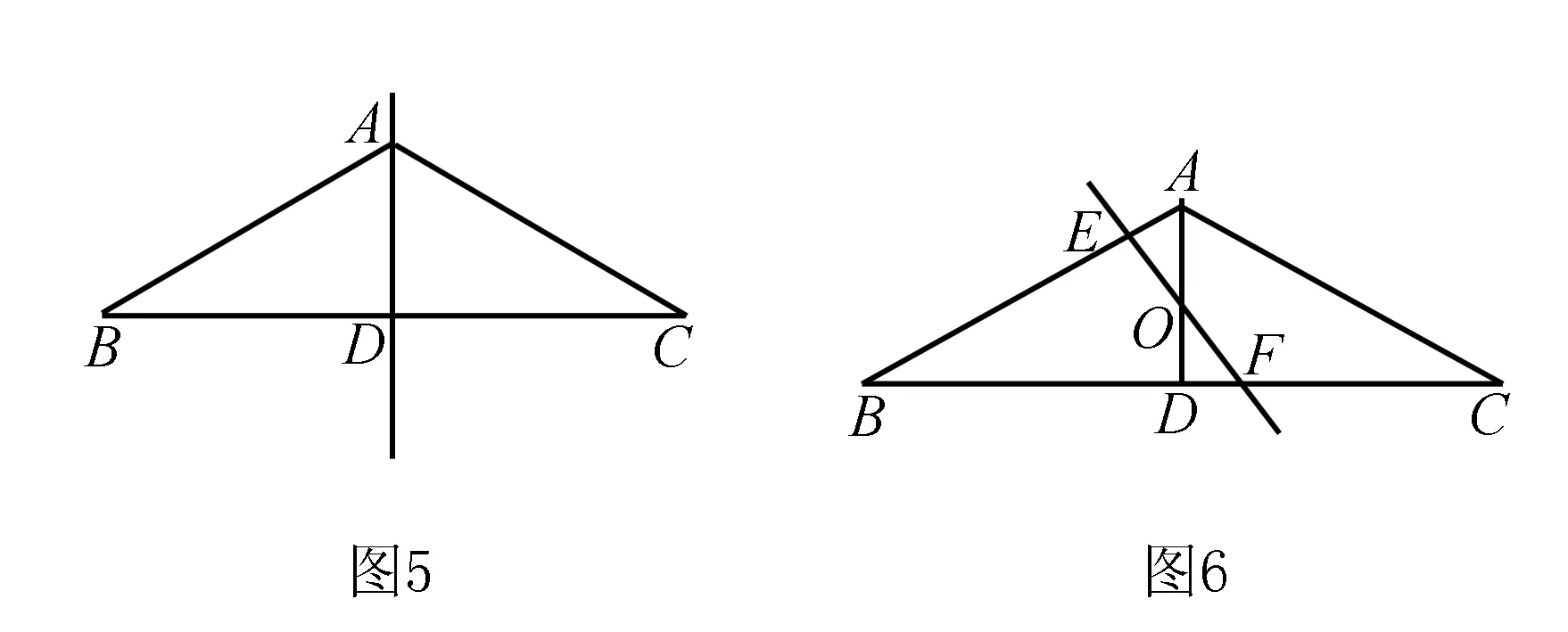
2.用心倾听,从基本图形着手


三、几点感悟
1.夯实基础知识,方能听见题目声音
2.熟悉基本图形,方能让题目说话
3.善于反思归纳,方能再听见题目声音
