问题串在初中数学教学中的运用

2018-06-01巢王卫

数理化解题研究 2018年14期

巢王卫

(江苏省丹阳市后巷实验学校 212312)

一、温故知新，提升问题串艺术性

在数学教学中，学生对知识接受能力差的一个重要因素是缺乏对问题的初步认知，难以在原有的基础上建立新的认知思考.在数学教学中，教师可结合问题串设计的艺术性原则，从原有的知识体系出发，搭建新旧知识间的联系.

例如在进行《圆》一课的教学时，圆是学生在小学阶段接触过的概念且圆的应用在生活中处处可见，在进行问题串设计时教师可依托学生原有的知识体系进行问题引申，并采用艺术性的提问内容和串联体系设计问题串.问题串内容如下：(1)给出自行车轮、硬币、摩天轮的照片，提问学生图片中的物体具有什么特点；(2)提问学生为什么要将自行车轮设计为圆形，三角形和正方形是否可以；(3)回忆如何画出圆，归纳圆的定义.结合学生原有的知识体系，教师设计了一组具有思考性和回顾性的问题.通过对圆的情境回顾，为学生搭建了生活和圆之间的桥梁，消除了学生在学习知识过程中的陌生感.借助(2)、(3)中的探究问题，引出了圆心到圆上各点距离相等的定义.相较于直接给出定义，提问的方式更具备探究性，最大程度地开发了学生的探究潜能.

二、有的放矢，确保问题串目的性

问题串不是简单的将问题进行集成，而是借助科学的分析方法和针对性的教学研究所涉及的与教学目标紧密相连的问题.在教学过程中，教师应在对教学目标进行充分研究的基础上设计问题，保障问题串的目的性.

例如在进行《三角形的中位线》一课的教学时，本课的教学重点在分析三角形和梯形中位线定理形成的基础上，掌握定理并能够解决实际问题.结合教学重点，教师所设计的问题串应从定理的导入、证明和推广三个层面开展，同时注重问题间的连贯性.教师所涉及的问题串如下：(1)回顾问题，△ABC中AB和AC边分别有一点E、D，如果DE∥AC，E为AC中点，那么点D呢；(2)引申问题，如果分别E、D为AB、AC中点，能否得出DE//BC；(3)引发探究：观察两个三角形，猜想二者间的关系，试证明.思考证明平行常用的方法(必要时提示辅助线)；(4)引导描述：试描述三角形中位线定理；(5)拓展应用：以三角形为基础推导梯形中位线定理.问题串中的四个问题与教学目标相对应，且前后问题之间存在联系性，体现了教学与问题的关联性.

三、层次渐进，注重问题串启发性

在问题式教学的开展过程中，教师引导性作用发挥的好坏在于教师所提供的问题是否具有启发作用.因此在问题串设计中，教师应关注问题的启发性，借助层次性的问题引导学生用心去思考、主动去呈现，进而实现知识内化.

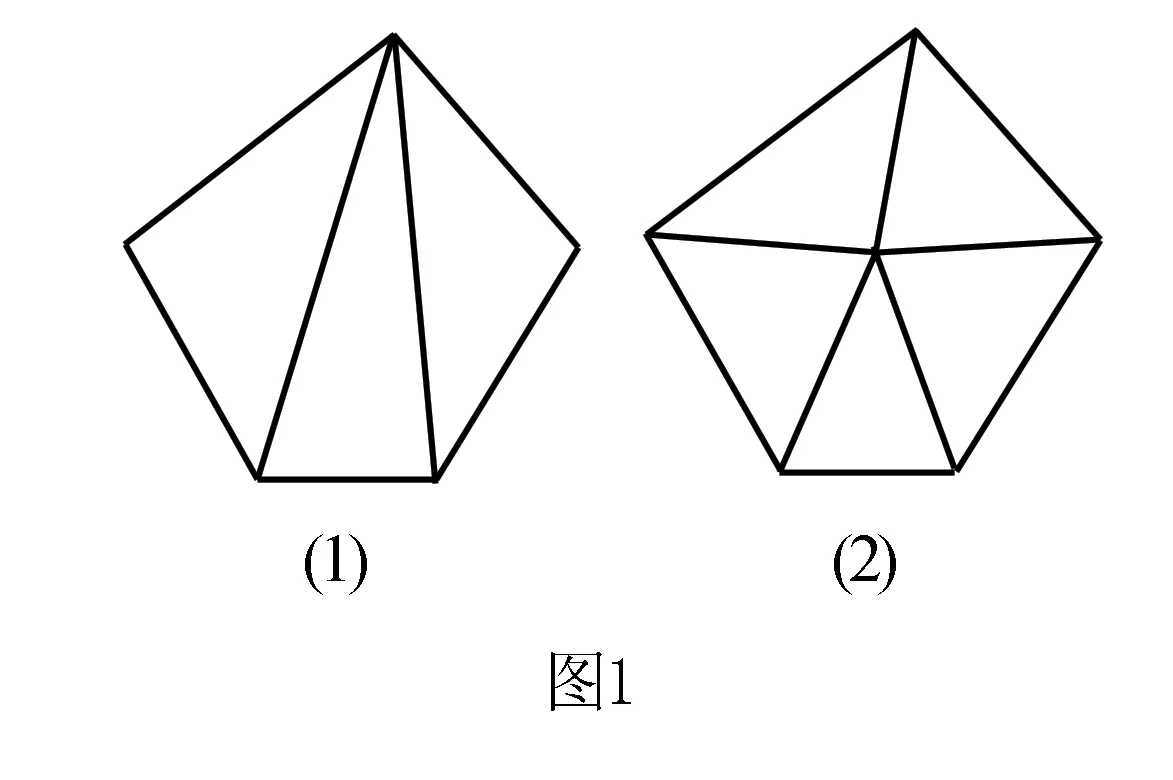
例如在进行《多边形的内角和与外角和》一课的教学时，为使学生深入理解内角和的推导过程并形成借助已知结论进行未知探究的思维能力，教师从浅层次的问题出发逐步诱导学生深入进行探究.教师设计问题串如下：(1)回顾三角形内角和为多少度；(2)在纸上画出五边形，并思考如何得出内角和(量角器)；(3)结合图1思考如何不借助量角器得出内角和；(4)你还有其他拆分方法吗(从顶点、边、五边形内任意一点)；(5)选择最为简单的拆分方法(从顶点拆分)，对于n边形内角和进行计算；(6)结合拆分个数总结n边形内角和公式.从浅层次的知识回顾和动手操作到深层次的联系思考，学生经历了解决问题的全过程并形成了未知到已知的转化方法.