中考数学阅读理解问题研究
2018-06-01许开宇
许开宇
(浙江省天台县白鹤中学 317201)
随着教育改革的实施,中学数学课程标准对学生的数学阅读能力提出了要求,要求在初中数学教学中要提高学生的数学阅读能力,提高学生分析问题和解决综合问题的能力.为此,中考数学出现了一种新的题型——数学阅读理解题,这一类题目设计的背景知识较为广泛,不仅能够帮助学生积累知识,还能够促进学生数学学习能力的迁移,提高学生利用数学方法解决数学问题的能力.
一、数学阅读理解问题概述
数学阅读理解问题主要是通过一段问题背景,这一背景可以是涉及到新的知识点或者新的解题过程,在解题的时候,首先分析背景知识中的有用信息,利用知识迁移、类比推理等方法,解决题目中提出问题的一类题型.
二、中考数学阅读理解问题整体特征
通过对近几年中考数学阅读理解问题的统计分析可以看出,中考数学阅读理解问题包含以下几种特征:第一,这一类问题的内容设置较为丰富,里边涉及到大量的信息,不局限于课堂教学内容,既有课堂上的内容,也有其他科目、生活实践等学生没有接触过的知识.第二,中考数学阅读理解问题对学生的阅读能力有较高的要求,学生能够灵活使用图像、文字、符号等语言,并且能够借助这些语言探究问题的本质.第三,中考数学阅读理解问题注重学生的解题过程,重点考察学生对材料中解题思路的探究情况.
三、中考数学阅读理解问题分类
1.中考数学阅读理解题目题型分类
通过对近几年中考数学题目的统计可以看出,数学阅读理解题题型涵盖了选择题、填空题和解答题三种题目类型.在选择题中,主要以新定义和新运算的题目为主,要求学生能够根据题目中已经给定的运算方式,来解决已经给出的与例题相似的问题.
例如:我们规定[x]是表示不大于x的最大正整数,例如[1.2]=1,[3]=3.[-2.5]=-3,如果[]=5,那么x的取值范围是多少?A.40 B.45 C.51 D.56
对于中考数学阅读理解类填空题来说,也是以新定义和新运算的题目为主,要求学生能够根据题目中已经给定的运算方式,来解决已经给出的与例题相似的问题.
例如:对于实数a,b的运算规则如下:a×b=,例如8×6,因为8>6,所以8×6=-8×6=16.方程-6x+9=0的两个根为,,那么×= .
2.中考数学阅读理解内容分类
根据题目的内容又可以将数学阅读理解问题划分为五个类型.第一类就是,给出一定的运算规则或者定义,借助这一知识来解决提出的相关问题.这一类问题重点考查学生对新知识的应用迁移能力,学生需要先将已经给出的新运算规则内化为自己的解题思路,然后再利用这一解题思路来来解决问题,是学生一个有意义学习的过程.例如:已知新的运算法则如下:对于实数a,b都满足a+b=a(a-b)+1,等式的右侧是我们基本的加减乘除运算,那么(-2)+3的结果是多少?
第二类就是根据材料中给出的解题思路,来解决类似的问题,这一类型的问题主要考查学生对材料中解题过程的理解和知识运用的迁移能力,一般情况下,这一类的问题难度不大.例如:将分式进行拆分,得出一个整式和一个分式的和的形式,解题过程如下所示:首先,设分子=,那么=-(m-1)+(m+n)因为对于任意实数a使得上述等式恒成立,那么m-1=1,m+n=3,所以m=2,n=1,所以==+=+.
那么请将分式拆分为一个整式和一个分式.
第三类就是涉及到图表和实际生活相结合的问题,这类问题首先会给出一段文字说明,然后给出图表,学生要能够借助文字中的信息去分析图表,然后去解决问题.例如:中华汉字源远流长,为了发扬传统文化,某校开展了汉子听写大赛,参赛的学生有3000人,通过对他们的成绩进行分析发现,所有学生的成绩都不低于50分,为了详细分析学生在此次比赛中的成绩,随机抽取了200名学生,具体成绩分布如下所示:
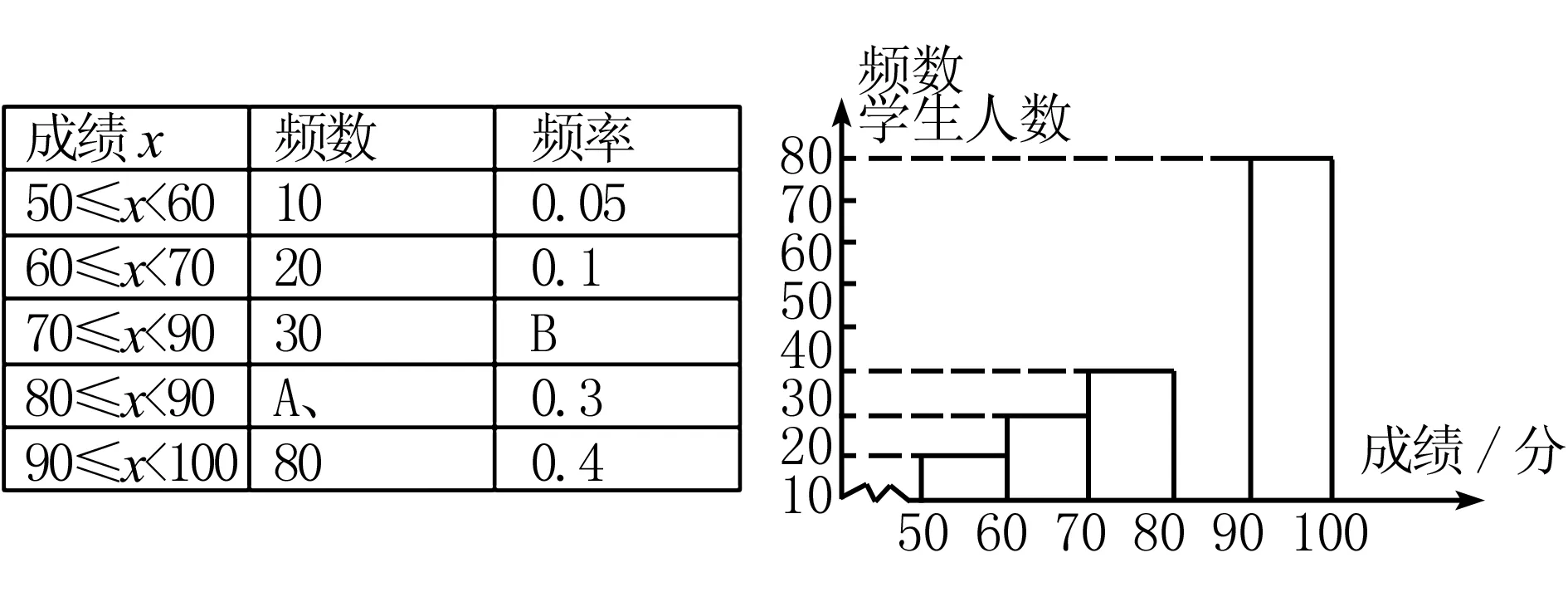
(1)a=b=
(2)请在直方图中补全相关信息
(3)这次比赛分数的中位数会落在那个分数段
(4)如果成绩达到90分以上则评定为优,其中包括90分,那么此次比赛能够被评为优的学生有多少?
第四类就是根据已经给出的阅读材料,去总结规律,然后去解答给出的问题,其中,根据题目中阅读材料中的隐含信息,总结规律是解决这类问题的关键所在.
第五类就是通过阅读给出的材料,解决相关的问题,对于这一类问题主要考查学生对知识的探究和应用,难度较大,一般情况下,中考数学很少出现这一类的问题.
总体上来说,中考数学阅读理解类题目的考查还是倾向于简答题,很多分值较高的阅读理解题目都是简答题,其考查的内容也主要集中在利用新规则、新运算来解决问题;借助材料中的相关问题的解法,来解决类似题目等.
参考文献:
[1]汤张霖,赵平.阅读理解题中考创新排头兵[J].中考金刊,2009(03):52-53.
[2]张建武.中考数学阅读理解题题型与解法例谈[J].理科爱好者:教育教学,2009,1(4):82-82.
[3]翟向阳.中考数学阅读理解题的解答技巧[J]. 考试周刊, 2010(22):10-11.
