升沉补偿样机系统的设计与实现

， ，， ，

(1.华中科技大学船舶与海洋工程学院，湖北 武汉 430074；2.武汉第二船舶设计研究所，湖北 武汉 430064；3.武汉空军预警学院，湖北 武汉 430019)

0 引言

船舶在海上作业时，由于波浪的作用，船舶会产生升沉运动[1]，而这会给海上起重机吊装作业带来不利的影响。通过设计合理的升沉补偿装置，便能使得波浪带来的不良影响降低到最小。目前国外有成熟的升沉补偿产品，但对国内进行关键技术封锁。而国内任处于研究阶段，目前并没有成熟的可用于实际工程的相关设备。考虑到距离实际工程应用还有一定难度，着手设计了升沉补偿样机系统，通过在样机上进行各种实验，以期能为将来的进一步研究提供有一定价值的参考。

升沉补偿装置可分为三类：被动型、主动型和复合型[2]。搭建的样机系统[3]采用复合型升沉补偿装置。

1 升沉补偿样机系统设计

1.1 关于试验样机的缩比说明

一般情况下，在搭建试验样机时，并非要完全的以1∶1的比例来参照实际工程原型系统。根据相似理论，使得样机系统与实际系统满足几何相似、时间相似和速度相似等，即可根据样机系统的试验效果来反推实际系统的性能。采用缩比样机能节约人力物力，且能反应实际原型系统的性能。

本课题之前的成果，参考文献[5]第6章，系统原型与缩比后的样机部分参数对比如表1所示。

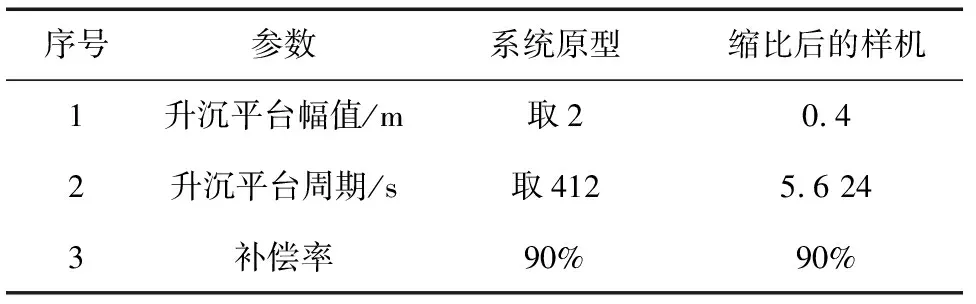
表1 系统原型与缩比样机部分参数对比

1.2 总体机械方案

图1为升沉补偿样机系统主视图。系统由整体支撑框架、升沉平台、伺服电动缸、卷扬机、液压缸、动滑轮组、定滑轮组和负载等组成。整体支撑框架起着支撑各个基本部件的作用，采用钢材料。伺服电动缸的推杆与升沉平台固联在一起，通过控制伺服电动缸的推杆的位移即可控制升沉平台的位移。升沉平台模拟的是海上的船舶。

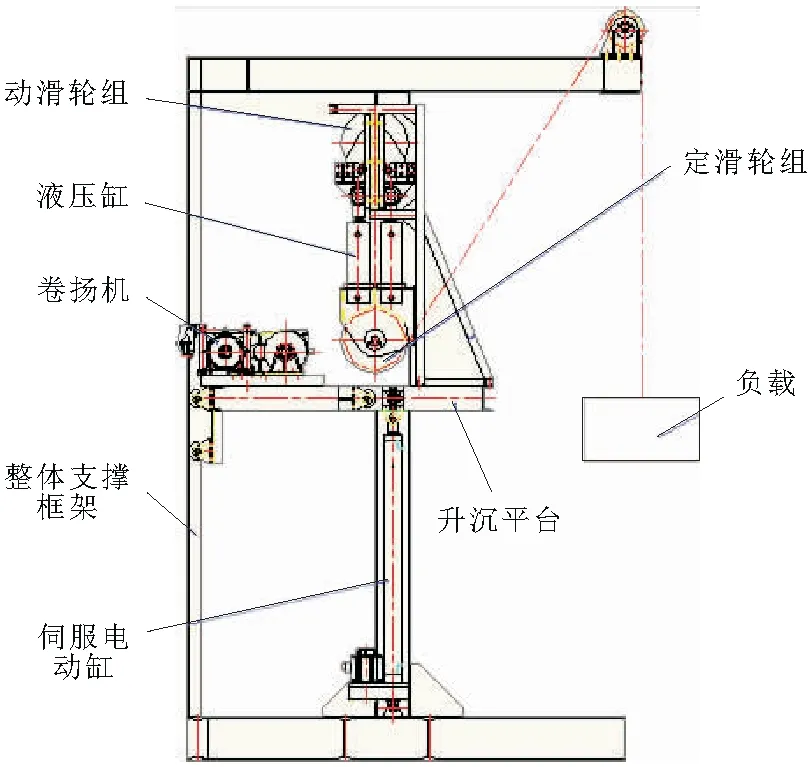
图1 升沉补偿样机系统主视图

通过控制伺服电动缸的运动，即可让升沉平台进行类似于船舶在波浪的扰动下的升沉运动。卷扬机与升沉平台固联在一起，模拟的是海上作业的船舶起重装备。液压缸是此样机系统的核心补偿装备，左边为被动液压缸，右侧为主动液压缸，被动液压缸与主动液压缸固联在一起，是相对静止的。考虑到，液压缸的行程较短，但是可持续输出的功率较大，于是采用了滑轮组的方式，静滑轮组与升沉平台固联在一起，而动滑轮组相对升沉平台是可以垂直上下运动的。钢丝绳连接负载与卷扬机的滚筒，并来回缠绕经过动滑轮与定滑轮，引入了滑轮组后，液压缸在竖直向上的方向工进一个单位的位移，则钢丝绳会收缩4个单位的长度，即对液压缸的作用进行了4倍放大。

只要控制液压缸的实时工进位移得当，则负载的位移可基本不受升沉平台的位移的影响。考虑特殊情况，若卷扬机的滚筒静止不动，则理想的结果是，负载相对地面是静止不动的。

1.3 总体控制方案

样机系统总体组成如图2所示。工控机作为整个样机系统的控制核心，基于Qt4设计了一个人机交互界面。可在工控机界面输入若干个变量参数，同时一些传感器采集回来的数据也在界面上显示。下位机采用的是S7-300PLC控制器。西门子S7-300PLC控制器具有运算速度快、可靠性高、保密性好以及能在恶劣的工业环境中使用的优点。伺服电动缸、各个液压阀和卷扬机都是通过PLC来控制的。工控机与下位机的通信采用的是成熟的以太网UDP通信，其协议简单、运用方便、可靠。负载可受到卷扬机，升沉平台和补偿器的影响。平台的位移可通过姿态仪测出。另外负载相对平台的位移可通过编码器测得，液压缸推杆相对液压缸缸体的位移也可通过编码器测得。

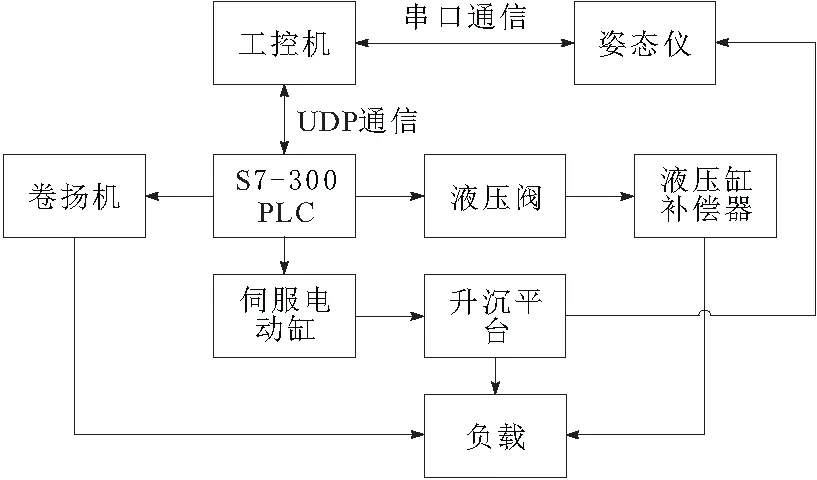
图2 样机系统组成

2 姿态仪信号处理

2.1 问题描述

姿态仪采用的是SBG Systems公司的IG-500E传感器。样机利用此姿态仪来获取实时的升沉平台的竖直方向的位移，但是在实验中发现，信号是存在较大的滞后，通过反复实验，可认为此传感器滞后时间约为0.6 s。姿态仪信号的滞后会给样机系统的控制效果带来不利影响，为了尽可能的消除影响，需要对信号进行处理。

2.2 信号处理

参考文献[4]，采用AR(P)模型对姿态仪信号进行实时的短时预报。设{xt,t=…,-1,0,1, …}为随机的时间序列，满足以下方程:

x(t)=Φ1x(t-1)+Φ2x(t-2)+…+

Φpx(t-p)+εt

(1)

上式称为AR(P)模型，p为模型阶次；εt为随机干扰误差项，是0均值的独立白噪声序列；Φ1，Φ2，…，Φp为自回归系数，表示x(t)依赖于过去的程度；x(t)为当前的预测值。

针对样机平台的升沉运动建立的AR(P)模型，需要确定其阶数p。采用的定阶准则是AIC准则。具体运用时，在规定范围内使模型阶数由低到高，分别计算AIC值，最后确定使其值最小的阶数，就是模型的合适阶数。

参照表1，设缩比样机升沉平台的运动函数为：

xs(t)=0.4sin(πt/6)

(2)

传感器的时延为0.6 s，采样周期取T=0.2 s，采用一阶保持器，则需要预报4步。通过仿真得图3。通过观察图3，可发现预报的位移与实际的位移非常接近，可以在样机控制系统中，用预报的姿态仪位移信号来代替实际的平台位移信号。

图3 采用一阶保持器的4步预报结果

3 前馈控制算法

3.1 动力学模型分析与简化

基于本项目组之前的工作，参考文献[5]，本系统的动力学传递函数[6]为：

{(-4mp-16mt)s2/[(mp+16mt)s2+

(3)

xh为负载位移；I为电磁比例阀的电流，xs为升沉平台位移。其余的动力学模型符号含义如表2所示。

表2 动力学模型各符号含义

这里把xs(s)看成是对系统的干扰。上式(3)表示，负载的位移由两部分叠加而成，一部分是人为主动的控制比例阀所引起的负载位移变动，另一部分是由平台的扰动而导致的负载位移的变动。

控制的基本思路是希望能把由平台的扰动而导致的负载位移尽可能的消除，如果采用普通的控制方法，往往滞后较大，难以达到理想的补偿效果。而采用前馈控制可以基本消除干扰。

通过代入实际数据进行仿真预观察，可以发现，平台通过以下这一项：

产生的扰动非常小，考虑工程习惯，这一项可以忽略不计。此外，这一项的扰动频率比较高，如果加入前馈补偿器，会导致比例阀[7]的频繁动作，对于比例阀的使用寿命是不利的。

于是式(3)可化简为：

(4)

3.2 前馈控制算法

采用了结构不变性原理来设计前馈补偿器。在I(s)项加入一个前馈补偿项:Gs(s)Xs(s)′。前馈补偿项中的Xs(s)′项是经姿态仪检测而来的信号，并经过处理后的的平台位移数据，而Gc(s)是前馈补偿器的式子。暂时认为，Xs(s)′=Xs(s)，那么通过设计一个恰当的前馈补偿器Gc(s)，便能使得平台的升沉运动对位移负载产生的干扰为0。经计算，得到Gc(s)如下所示：

Gc(s)=

(5)

Gc(s)分子阶数大于分母阶数，在物理上实现是有困难的。可以在分母项乘上(1+Ts)3，只要令T足够小，便不会引入太大的误差，取T=0.01。Gc(s)变为：

Gc(s)=

(6)

系统的控制原理图如图4所示。R(s)表示的是负载的目标位移，主回路采用的是PID算法，Xs(s)表示的是样机升沉平台的位移，Xs′(s)表示的是姿态仪接收到的且经过预报处理的升沉平台位移数据。G1(s)表示的是系统通过控制比例阀来影响负载位移的传递函数，而G2(s)表示的是样机升沉平台的位移对负载位移的作用的传递函数。而Gc(s)表示的是前馈补偿控制器。从理论上来说，若预报的精度足够高，则基本能把平台的升沉对负载位移的干扰消除掉。

图4 控制原理

4 实验与误差分析

4.1 实验

在缩比样机搭建完成后，参考表1，设置平台参数是，升沉平台的运动近似为正弦运动，幅值为0.4 m，周期取12 s。不失一般性，令卷扬机角速度为0 rad/s。具体的姿态仪信号处理、前馈算法和PID算法在上位机中实现。启动平台进行实验并记录数据，补偿效果如图5所示。

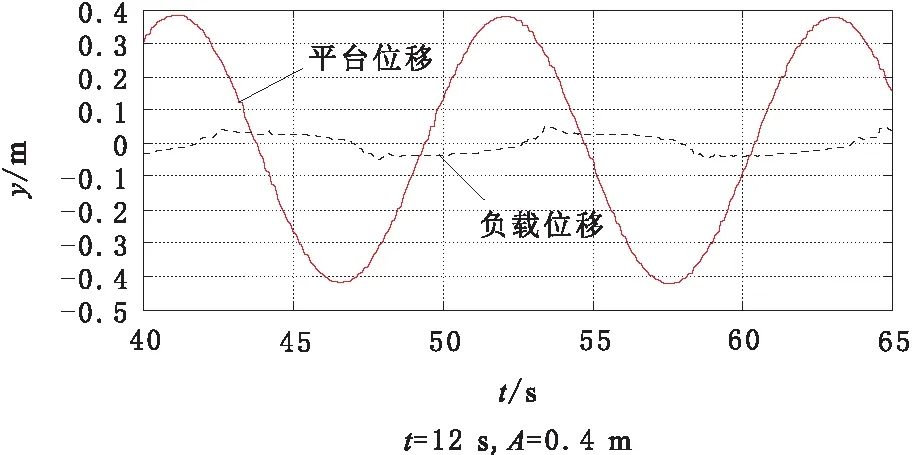
图5 样机补偿效果

一般升沉补偿的补偿率是指，由平台升沉位移导致负载位移的波动的最大绝对值/平台升沉位移的最大绝对值。

通过观察图中数据，负载位移的最大绝对值约为0.039 m，平台位移的最大绝对值约为0.415 m。则补偿率为1-0.039/0.415=90.6%

可发现样机系统的补偿率[8]在90%左右，达到了预期目标。充分说明了思路的正确性。

4.2 误差分析

尽管本文的补偿率在达到了90%左右的要求，但是还有提升空间的。本样机系统主要的误差来源于以下4个部分：

①在上文中，分析升沉平台的位移对于负载的扰动时，进行了简化，忽略了一项作用比较小的项。

②针对姿态仪的信号处理与预报总是会存在误差，不可能完全的实时重现升沉平台的运动位移数据，这个误差会体现在降低补偿率上。

③考虑到工程上的实现的方便，在前馈补偿控制器的设计中，在分母中引入了(1+Ts)相关项，这一步骤也会引入误差。

④作为样机系统，工程与理论上存在着许多的不同点，在建立系统动力学模型时，已经进行了简化，而这也会引入误差。

5 结束语

搭建了一个升沉补偿样机平台，对其基本构成进行了详细分析。对姿态仪的信号延时问题进行了实时的预报处理，并基于结构不变性原理设计了前馈控制器。通过在实际样机上进行实验，达到了补偿率在90%的补偿效果[9]。分析了本实验样机的误差来源，为将来的改进方向提出了建设性意见。总体来说，通过此升沉补偿样机的研制，给将来实际工程应用打下了坚实的基础。

参考文献：

[1] 曾智刚．波浪运动升沉补偿液压平台关键问题试验研究[D]. 广州：华南理工大学，2010.

[2] 吴隆明．深海作业起重机主动式升沉补偿控制系统的研究与开发[D]. 广州：华南理工大学,2012.

[3] 杨东超，唐国元．滑模控制在升沉补偿系统中的应用[C]//聚焦应用 支撑创新——船舶力学学术委员会测试技术学组2016年学术会议论文集,2016：295-301.

[4] 鲜玲．深海作业起重机主动式升沉补偿预测模型算法研究[D]. 广州：华南理工大学,2014.

[5] 高磊．船舶甲板吊放设备升沉补偿系统研究[D]. 武汉：华中科技大学,2015.

[6] 杨叔子，杨克冲，吴波，等．机械工程控制基础[M].武汉：华中科技大学出版社，2005.

[7] 王春行.液压控制系统[M].北京：机械工业出版社,1999.

[8] DRISCOLL F R，LUECK R G，NAHON M.Development and validation of a lumped mass dynamics model of a deep sea ROV system[J]. Applied Ocean Research, 2000, 22(3) 169-182.

[9] ZHANG Y T，LI A，ZHANG W K，et al.Virtual experiment and research for heave compensation system [C]//Proceedings of the 2011 International Conference on Fluid Power and Mechatronics, 2011:270-275.