水下柔性驱动小车受限运动控制研究

， ， ，

(华中科技大学船舶与海洋工程学院，湖北 武汉 30074)

0 引言

水下柔性驱动小车用于为水下装备及相关传感器提供水下环境中的动态试验平台，满足其性能检测的环境要求。考虑到液压马达速度伺服系统诸多优点，响应速度块、功率/质量比大、负载刚性高和性价比高等，系统选用阀控液压马达来驱动绞车滚筒[1-2]，绞车滚筒通过钢缆连接至水下小车。

许多先进控制策略被引入电液调速系统，如模糊控制、自适应控制、神经网络控制、滑膜变结构控制和预测控制等，在避免外界扰动、降低系统参数时变等不确定因素对系统调速性能的影响上已有较好表现[2-9]。但考虑到本系统由于复杂结构特及特殊应用环境而衍生出的一些列控制难点，包括柔性变负载、大惯量、参数时变、滞后非线性等。因此，提出一种F+PID 复合控制算法，并设计专用控制系统，以满足水下受限空间内柔性驱动小车的运动控制要求。

1 控制系统及原理

1.1 水下柔性驱动系统

水下小车柔性驱动系统是利用液压马达直接或者通过减速箱来拖动绞车滚动而实现水下小车进退的一类驱动系统。该系统是典型的机电液一体化系统，主要由液压系统、控制台、工作机构三部分组成。液压泵站为液压绞车提供所需压力油。控制台输出相应控制信号。工作机构包括牵引绞车、制动绞车、导轮等，通过液压绞车上滚筒的旋转带动钢丝绳收放，从而实现水下小车在限制行程内前进后退。

1.2 液压系统

水下柔性液压驱动系统主要由主泵站、蓄能器组、控制阀件、牵引绞车、1台制动绞车及油箱组成。

系统开始工作前，液压泵给主液压动力源供油，经过单向阀后，到达卸荷溢流 ，进而给动力蓄能器组充油 。动力蓄能器组存储高压油液，当驱动水下小车运动时，蓄能器组向系统提供所需液压能 。液压油从动力蓄能器组输出后，经过减压阀减压至23 MPa ，并通过稳压蓄能器降低压力波动，使控制牵引绞车和制动绞车的伺服比例阀前端压力保持在23 ～22.2 MPa范围内，以降低控制难度。

控制器根据控制策略及算法实时调整伺服比例阀输入电压，伺服比例阀自带闭环反馈，严格保证阀芯位移与控制信号成正比例，当阀芯开度达最大时，流量达1 500 L/min (阀压降为1 MPa) ，满足系统流量需求。

1.3 水下柔性驱动小车受限运动控制原理

图1为限运动控制系统原理图。系统采用闭环反馈的方式进行控制，通过速度传感器采集水下运载器速度，与预设速度对比得出速度偏差及速度偏差变化率，然后给到复合控制器，计算出下一时刻伺服阀芯开度，进而控制液压绞车的转速与行程，最终实现对水下小车的运动控制。

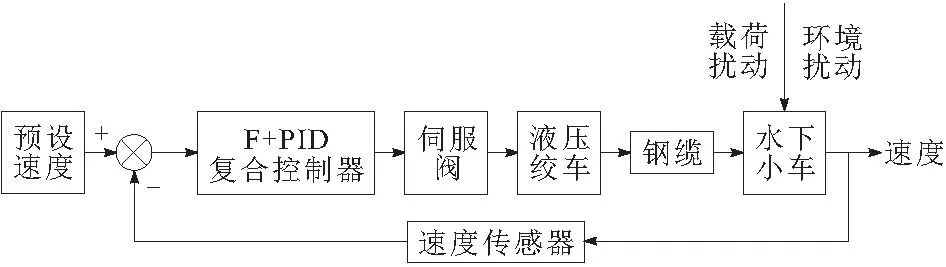
图1 水下柔性驱动小车受限运动控制系统原理

2 水下柔性驱动小车受限运动控制的F+PID复合控制器设计

2.1 控制任务要求

控制系统需驱动系统驱动水下小车在试验水池底部的轨道上完成加速、匀速、减速动作。其中匀速段速度要求达到2.5 m/s ，持续2 s 。速度偏差须控制在±0.2 m/s 范围内，总行程不超过12 m。

2.2 控制器设计

经前期分析得出，水下小车柔性驱动系统是典型的复杂负载系统，其主要特点有，① 刚度不足易失稳，系统采用钢丝绳连接，钢丝绳本身的弹性及柔性导致系统整体刚度不足，小车驱动系统易失稳[10-11]； ②时滞非线性，液压系统内部存在迟滞特性，同时液压系统参数随着油温变化，负载随速度变化，进一步增加系统非线性和参数时变性[1]；③大惯量，瞬时功率要求高，水池底部轨道有效行程受限，需在短行程内驱动小车加速至到2.5 m/s 的速度并保持2 s；④冲击变负载，当小车在运行时，受到的阻力，包括流固耦合作用力、兴波干扰力以及池壁效应阻力；另外，匀速运行阶段中，会出现持续性的冲击载荷干扰；⑤协同驱动难控制，水下小车由两套驱动机构前后串连协同牵引，两套驱动机构牵引效率不同。

针对该系统柔性变负载、大惯量、参数时变、滞后非线性等特点，控制策略的设计应满足如下要求，① 加速阶段中，小车的速度只增不减，保证牵引侧钢缆始终呈张紧状态，避免造成振荡；②为了保证系统的快速性，制动侧缆绳上的张力应尽可能小或者为0，但也不宜过分松弛，以免减速瞬间缆绳张力冲击过大。

2.2.1 F+PID复合控制器设计

F + PID 复合控制器如图2所示，它包含Fuzzy控制模块、PID控制模块、切换模块和匀速阶段冲击补偿模块。在输入速度偏差之后，设置一个带阈值的模态 (每种控制方式为一种模态) 转换器，根据阈值与e的比较结果确定模态：当e大于阈值时，让信号传输到F控制器，以获得良好的瞬态性能；若e小于阈值，则让信号传输到PID控制器，以获得良好的稳态性能，F+PID阈值设置为2%。

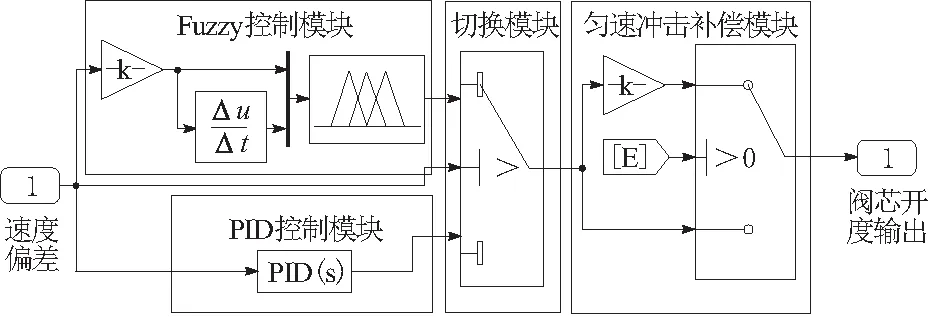
图2 F+PID复合控制

另外，针对匀速阶段中存在的0.8 s冲击变负载，在负载冲击前增加一定比例的阀芯开度输出，依靠液压系统的自适应性克服瞬时冲击对小车速度的影响，保证运载器运行状态的稳态性能。在这部分中，匀速冲击补偿比例设定为原阀芯开度的115%。

该种F+PID复合控制器，比单个的模糊控制器具有更高的稳态精度；而比经典的PID控制器具有更快的动态响应特性，使系统能更快地趋向平衡点，且能更加灵活的处理瞬时冲击[12]。

2.2.2 Fuzzy 控制模块设计

考虑到水下柔性协同拖曳的小车特性，选用 Mamdani 模型完成模糊控制任务。设置2个模糊输入变量，分别为速度偏差ve(理想速度videal- 实际反馈速度vfeedback) 和速度偏差变化率vec(单位时间内的偏差改变量) ，输出模糊变量为液压绞车伺服阀的阀芯位移 。

定义输入变量ve的模糊论域为{0，100%}，模糊子集为{100%，91%，73%，50%，30%，5%}；vec的论域为{0，300}，模糊子集为{ZERO ，PS，PB}; 输出变量的模糊论域为{0，100%}，模糊子集为{40%，50%，60%，70%，80%，90%，100%}。模糊控制模块的模糊规则设计如表1所示。

表1 模糊控制规则

3 水下柔性驱动小车受限运动控制系统建模

3.1 柔性驱动系统建模

图3是水下小车柔性驱动系统的受力分析图，假设绞车和滑轮组的运动方向是正向。滑轮组、牵引绞车、制动绞车的角速度分别定义为ω1,ω2,ω3,ω4,ω5和ω6。考虑到液压绞车、滑轮组和水下小车的布置位置，钢缆可分成6部分 (L1,L2,L3,L4,L5,L6) 。为了方便起见， 每个部分的张力分别定义为F1,F2,F3,F4,F5和F6。水下小车所受合力分别为前向牵引力F2、后向制动力F1和阻力f。

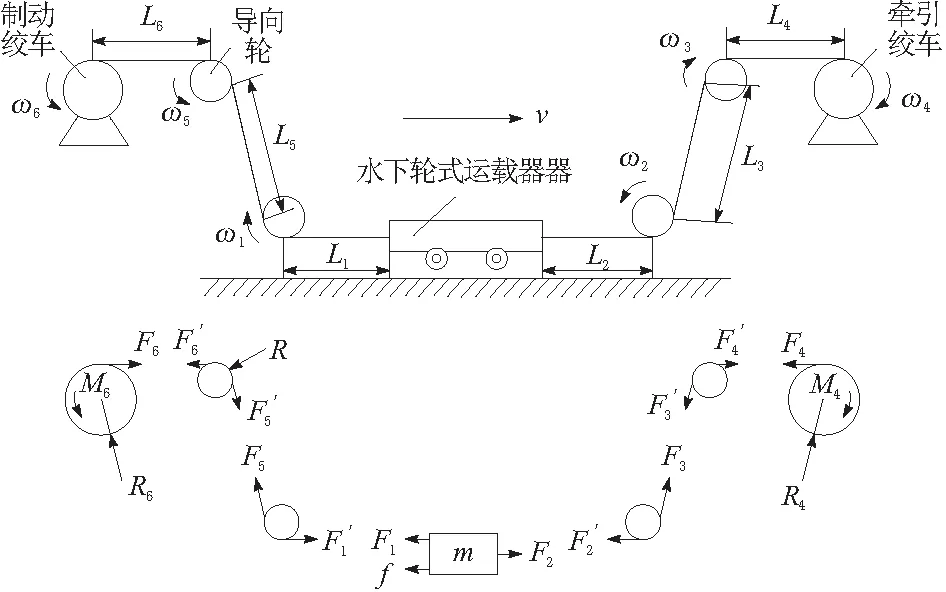
图3 由液压绞车柔性驱动的水下小车受力分析

在受力分析的基础上，得小车动力学方程为：

(1)

F1为水下小车后部F1段钢缆上的张力；F2为运载器前部L2段钢缆上的张力；f表示水下小车受到的水阻力；m表示水下小车的质量；vl表示水下小车的运行速度。

由于钢缆的非线性以及分布在两个方向上力的耦合性，需要对此水下柔性驱动系统的重要组成部分——钢缆进行受力分析。基于Kelvin-Voigt 模型[2]。在拉伸条件下，各段的变形量分别表示为Δxi(i=1,2,3,4,5,6)。考虑钢缆的两种状态，各部分钢缆上的张力为：

(2)

6段钢缆具有相同弹性模量和粘性系。考虑到系统运动时的状况，绳子各部分的动态伸长量为：

(3)

xl是水下小车的运行距离。

当小车在加速行程中时，后向制动力作为阻力，若要使速度快速上升，后向制动力应尽可能小。因此，F1可视为0。联立式 (1) 和式 (2) ，可得到如下简化的动力学方程：

(4)

将式 (3) 带入式 (4) ，并进行拉普拉斯变换，可得：

k2ω2(s)R-k2vl(s)+c2ω2(s)Rs-c2vl(s)s=

Mvl(s)s2+fs

(5)

3.2 液压绞车系统建模

为了计算液压绞车的传递函数，需联立液压驱动阀流量方程、液压马达流量连续方程和马达扭矩平衡方程3个基本方程。它们的拉普拉斯变化式为：

(6)

Ts为液压马达产生的理论扭矩；Jm为换算于液压马达转动轴上的转动惯量；Bm为负载和液压马达的粘滞阻尼系数；G为负载扭转弹簧刚度；Tl作用于马达轴上的外部负载扭矩。

通过联立3个基础方程，消除中间参数，输出阀芯开度与小车速度的传递函数如下：

(7)

ωh为等效液压固有频率；ξh为液压阀控马达的阻尼系数；Kce为常规流量-压力系数[1,13]。

3.3 外负载建模

水下小车柔性驱动结构的受力分析如图7所示。根据液压绞车的扭矩平衡方程，可得：

(8)

联立式 (3)、 (7)和 (8) ，液压扭矩平衡方程可写成如下形式：

Tl=R4Msvl+R4f

(9)

水下小车的水阻力模型表示如下：

(10)

3.4 小车速度控制器建模

根据实际测量速度和理想速度之间的偏差， F+PID 复合控制器计算得到下一时刻伺服阀阀芯开度Xv，并将控制信号输出到伺服阀，控制液压绞车输出驱动力矩，结合外负载力矩Tl和水阻力f，作用于水下小车上，最后模型输出小车的实时速度vl。

为了计算运载器运行速度和伺服比例阀阀芯开度之间的传递函数表达式，必须简化以上传递函数。方便起见，替换变量定义如下：

(11)

基于以上等式，可得：

vl(s)=ACXv(s)-BCR4Msv(s)-

(BCR4-D)f(s)

(12)

Xv(s)为伺服比例阀控制输入；v(s)为最后测量阶段内水下小车运行速度；f(s)为作用在运载器上的水阻力。

4 仿真及试验

在实际设备选型的基础上，液压柔性协同拖曳系统的主要额定参数见表2。

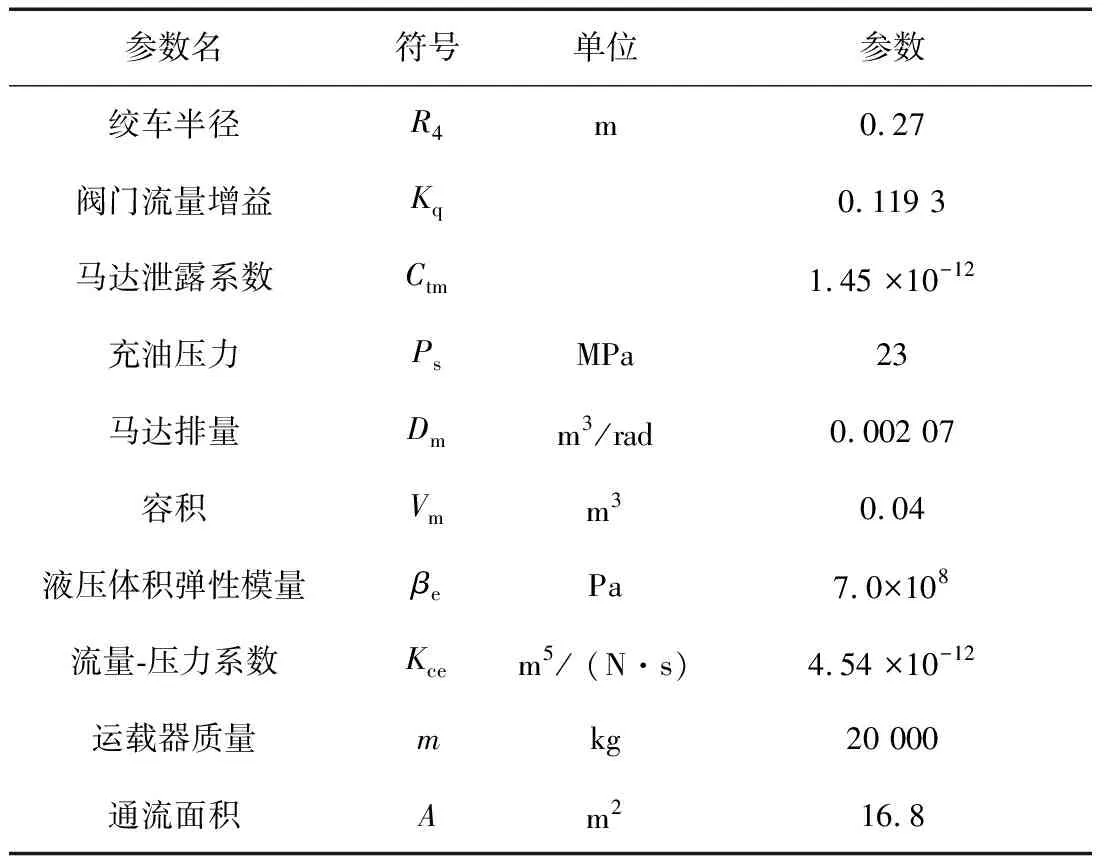
表2 液压柔性拖曳系统参数

带入表2中参数，水下柔性驱动小车受限运动控制系统的传递函数可写作：

(13)

4.1 全数字仿真

在简化模型的基础上，搭建水下柔性驱动小车受限运动控制系统模型。模型从左至右分别由理想速度曲线给定模块、F + PID Controller、牵引绞车模型、制动绞车模型和水下小车模型组成。

4.1.1 对比理想速度、F+PID控制器跟随速度、PID控制器跟随速度

在这部分中，F + PID复合控制器中的PID参数设置为PF+PID=2.5 ,IF+PID=0.5 ,DF+PID=0.142 ; 经典PID 控制算法的控制参数设置为PPID=2 ,IPID=0.8 ,DPID=0.1。

如图4所示，无论是经典PID控制还是改良后的F+PID控制，在没有瞬时冲击的情况下，均能在较短的上升时间内到达目标速度。

图4 速度曲线对比

但F+PID复合控制器比经典PID控制器具有更快速的稳定能力，在到达预定速度后，超调更小，静态偏差更小。

4.1.2 脉冲扰动下的仿真结果对比

设置一组受到脉冲干扰的对比试验来验证上述F+PID 复合控制器的鲁棒性，试验结果如图5所示，在这部分中，对正在运行两种控制算法的仿真模型施加一个0.8 s的负方向脉冲干扰，观察小车速度变化情况。扰动下的 F + PID 复合控制器速度响应仅出现微小波动，速度偏差保持在 ±0.1 m/s 内，且仍可收敛到预定速度，满足控制任务要求。然而经典 PID控制器的速度响应出现了较大波动，速度偏差超出控制任务要求规定的 ±0.2 m/s ，且当冲击扰动结束后，也有较大波动。

此组对比试验可以看出，F + PID复合控制算法在应对瞬时冲击时，有更好的鲁棒性。

图5 脉冲扰动下的速度曲线对比

4.2 半实物仿真联调试验

在实际控制设备生产加工完成后，搭建基于MATLAB/Simulink 和 VxWorks 实时系统的半实物仿真平台。半实物仿真平台由1台监控主机和1台对象仿真机组成 。

通信建立后，控制台根据预设速度与反馈的小车速度，计算后输出阀芯开度信号到正在运行柔性驱动系统和水下小车模型的对象仿真机上。仿真机模型根据控制台给出的阀芯开度信号，实时更新状态参数。图6为半实物仿真联调过程中的各项参数，可以看出，在整个水下小车运行过程中，控制台的功能正常，且水下小车上的速度响应和偏差响应均表现良好。

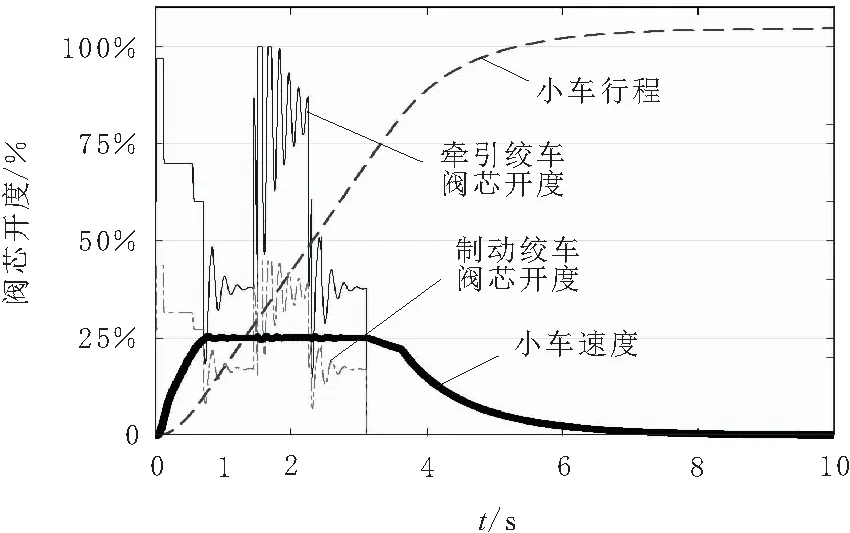
图6 半实物仿真数据曲线

5 结束语

针对水下柔性驱动轮式小车进行了小车在水下受限空间下的运动控制研究。根据水下小车以及柔性驱动控制系统的柔性变负载、大惯量、参数时变、滞后非线性等特点，采用F+PID 复合控制方法对小车运动实现模糊切换控制。全数字仿真试验结果证明这种控制方法不仅在快速性、稳定性上符合控制要求，而且在冲击变负载的扰动下，速度波动的偏差仍可保持在控制任务要求内。

另外，由于整体系统除控制台已集成完毕外，其余部分尚在建设中，暂无法进行实际对象试验。因此，使用半实物仿真平台为控制系统提供模拟对象，对已集成F+PID 控制器的控制台进行功能测试及部分性能测试，控制效果得到初步验证。后续待整套系统建设完毕，将进行基于实际对象的控制算法验证和调试。

参考文献：

[1] 唐守政. 钢丝绳在冲击载荷作用下动力学性能研究[D].太原: 太原科技大学, 2013.

[2] 倪松远. 钢丝绳机械性质的研究[D].哈尔滨: 东北林业大学, 2004.

[3] 赵亮. 液压提升机电业比例伺服系统研究[D]. 徐州: 中国矿业大学, 2011.

[4] 赵敬伟,孔祥臻,蒋守勇，等. 液压阀控马达速度系统模糊神经元控制与仿真[J].机床与液压.2011, 39 (17):111-112.

[5] XIANG X B, LIONEL L,BRUNO J.Smooth transition of AUV motion control: from fully-actuated to under-actuated configuration[J]. Robotics and Autonomous Systems. 2015, 67(5): 14-22.

[6] YU C Y, ZHANG Q, XIANG X B. On intelligent risk analysis and critical decision of underwater robotic vehicles[J].Ocean Engineering, 2017, 140: 453-465.

[7] WANG N, SUN J C, HAN M. Adaptive approximation-based regulation control for a class of uncertain nonlinear systems without feedback linearizability[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017.

[8] QI H W. Velocity control system for high inertia loads based on switch mode hydraulic power supply[J]. Chinese Journal of Mechanical Engineering.2004, 2 (9) :106-10.

[9] 程坷飞. 基于 T_S 模型的比例变量泵模糊控制系统[J]. 液压与气动.2007, 7 : 37-40.

[10] 李帅. 自整定模糊 PID 在改善泵控马达动态特性中的应用[J]. 液压气动与密封. 2009, 3:18-22.

[11] 桑勇. 基于广义预测控制的泵控马达调速系统的研究[J]. 湖南科技大学学报(自然科学版).2007, 22 (4): 34-37.

[12] 石辛闵，郝整清. 模糊控制及其MATLAB仿真[M]. 北京：清华大学出版社, 2008.

[13] 吴振顺. 液压控制系统[M]. 北京： 高等教育出版社, 2008.